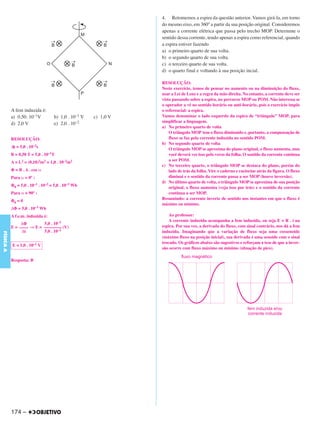
Este documento apresenta cinco problemas de física relacionados à mecânica newtoniana. O primeiro problema descreve um móbile pendurado e pede para calcular as forças de tração nos fios. O segundo problema descreve um experimento para medir o tempo de reação e pede para explicar por que a distância percorrida aumenta mais rápido que o tempo. O terceiro problema descreve dois corpos conectados por um fio e caindo livremente, pedindo para indicar as forças no fio. O quarto problema discute concepções prévias




























![C4_CURSO_FIS_A_Alelex 03/03/12 11:04 Página 173
RESOLUÇÃO:
MÓDULO 33 Quando o ímã se movimenta no tubo de cobre, há uma variação do fluxo
magnético que provoca o aparecimento de uma corrente elétrica induzida.
INDUÇÃO ELETROMAGNÉTICA: De acordo com a Lei de Lenz, a força magnética gerada neste anel de cobre
deve opor-se a esse movimento, assim, a corrente elétrica induzida tem
LEI DE FARADAY – F. E. M. INDUZIDA sentido horário, de acordo com a regra da mão direita.
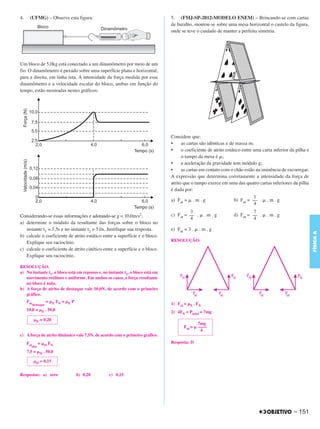
1. (UNESP-2012) – O freio eletromagnético é um dispositivo no
qual interações eletromagnéticas provocam uma redução de velocidade
num corpo em movimento, sem a necessidade da atuação de forças de
atrito. A experiência descrita a seguir ilustra o funcionamento de um
freio eletromagnético.
Na figura 1, um ímã cilíndrico desce em movimento acelerado por
dentro de um tubo cilíndrico de acrílico, vertical, sujeito apenas à ação
da força peso.
Na figura 2, o mesmo ímã desce em movimento uniforme por dentro
de um tubo cilíndrico, vertical, de cobre, sujeito à ação da força peso
e da força magnética, vertical e para cima, que surge devido à corrente As linhas de indução magnética no ímã estão saindo do polo Norte e
chegando ao polo Sul.
elétrica induzida que circula pelo tubo de cobre, causada pelo
Resposta: A
movimento do ímã por dentro dele.
Nas duas situações, podem ser desconsiderados o atrito entre o ímã e
os tubos, e a resistência do ar.
2. (UFTM-2011) – De quanto deverá ser a magnitude do choque
elétrico (f. e. m. induzida) se segurarmos as extremidades de uma
bobina composta por 10 espiras de área A=1 [m2] e deixarmos passar
ortogonalmente por esta bobina uma densidade de fluxo magnético
constante com módulo dado por B=11 [T]?
a) 0 [volt] b) 10 [volts] c) 110 [volts]
d) 220 [volts] e) 100 [volts]
RESOLUÇÃO:
Fluxo constante ⇒ ΔΦ = 0
Não haverá indução e a força eletromotriz induzida é nula.
FÍSICA A
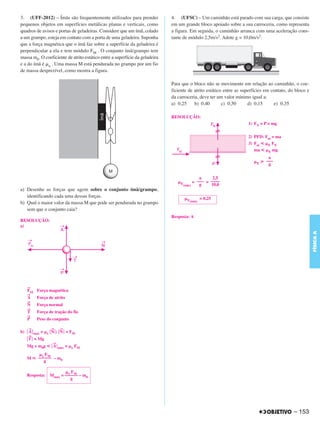
Considerando a polaridade do ímã, as linhas de indução magnética Resposta: A
criadas por ele e o sentido da corrente elétrica induzida no tubo
condutor de cobre abaixo do ímã, quando este desce por dentro do tubo,
a alternativa que mostra uma situação coerente com o aparecimento de
uma força magnética vertical para cima no ímã é a indicada pela letra
3. (MODELO ENEM) – Faraday, em seus primeiros experimentos,
buscou uma relação entre o fluxo magnético e o fenômeno da indução
magnética. Concluído seu trabalho, passou a buscar uma equação
matemática para relacionar as grandezas envolvidas e chegou à
segunda lei da indução:
ԽΔΦԽ
E = –––––
Δt
Nessa equação, temos:
E = módulo da f.e.m. induzida
ԽΔΦԽ = módulo da variação do fluxo magnético na bobina
Δt = tempo decorrido na variação de fluxo
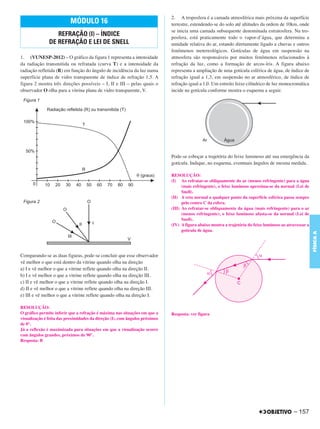
Um espira quadrada, de lado L = 10 cm, imersa no campo magnético
de um ímã, de intensidade B = 0,50 T, dá 1/4 de volta em torno de seu
eixo diagonal (ver figura) em 5,0 centésimos de segundo.
– 173](https://image.slidesharecdn.com/c4cursoaexerciciosproffisica-120715082023-phpapp02/85/C4-curso-a_exercicios_prof_fisica-37-320.jpg)