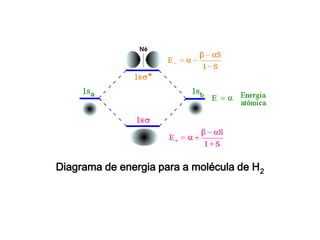
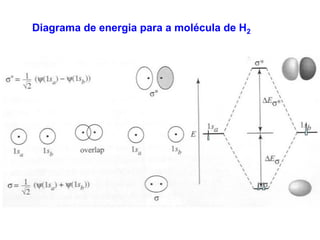
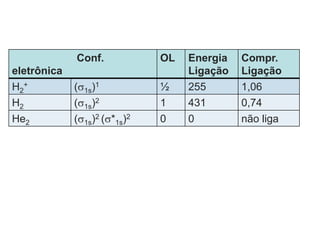
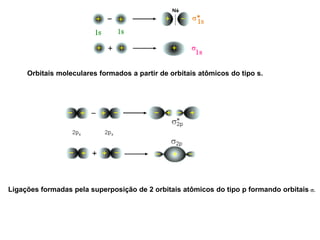
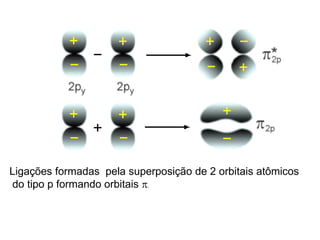
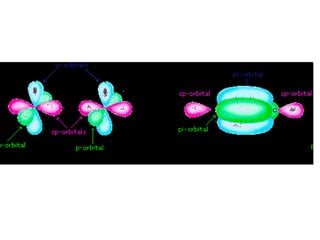
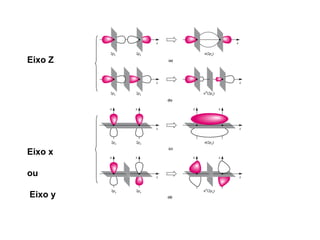
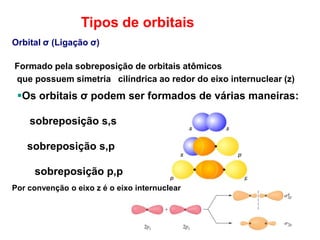
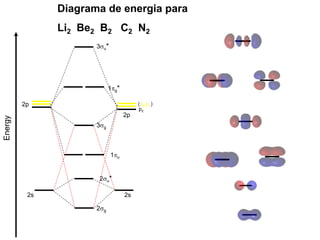
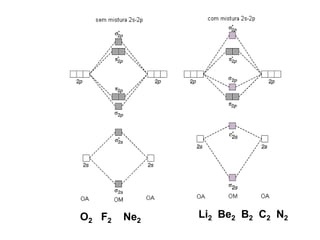
O documento discute a teoria dos orbitais moleculares para explicar as propriedades de moléculas diatômicas. Apresenta como os orbitais atômicos podem se combinar de forma construtiva ou destrutiva para formar orbitais moleculares ligantes ou antiligantes. Explica como calcular a energia destes novos orbitais e predizer a ordem de ligação e a energia de ligação de moléculas como H2 e He2.

2. Ligação covalente
Teoria deve explicar:
Diagramas de níveis de energia molecular
propriedades magnéticas e espectrais
Paramagnéticos
vs.
Diamagnéticos
Transições Eletrônicas
Estado Sólido – Condutância
Predizer a existência de moléculas
Ordem de ligação

3. OrbitaisMoleculares
Orbital Molecular resulta da combinação de orbitais atômicos.
Se os orbitais são funções de onda, podem se combinar tanto
construtivamente
(formando um orbital molecular ligante),
ou destrutivamente (formando um orbital molecular antiligante).

5. Amplitudes de funções
de onda somadas
(mesmo sinal de fase)
Amplitudes de
funções de onda
subtraídas (sinal de
fase oposto)
.

6. Teoria do Orbital Molecular TOM
Moléculas Diatomicas
Interferência destrutiva: orbitais de mais alta energia
(desfavorece a ligação) orbitais antiligantes
No caso de moléculas diatômicas as interações são facilmente
entendidas como provenientes das interferências construtivas e
destrutivas entre ondas dos elétrons (orbitais).
Interferência construtiva: orbitais de mais baixa energia. (favorece
a ligação) orbitais ligantes
(referência orbitais atômicos)

7. z

8. 0.735 Å
(H2)

9. Como saber se o modelo é adequado?
Calcular energia dos novos orbitais...................
),)(),),ˆ RRERR 111
(r(r(rH:RESOLVER  

10. H2

Hdemoléculaaparanohamiltonia +
2
O pordadoé
H  
2
2me
e
2
elétrondocinéticaenergia

e2
4o
1
rA1
por A1el.doAtração

e2
4o
1
rB1
Bpor1el.doAtração

e2
4o
1
R
rA1
A B
1
rB1
R
BeAentreRepulção

11. Curvas de energia potencial
molecular
calculada e experimental
para a molecula-ion H2
+
E  E1sH 
J+K
(1+ S)

e2
4o
1
R
E = E1sH 
J- K
(1- S)

e2
4o
1
R

12. MolecularOrbital
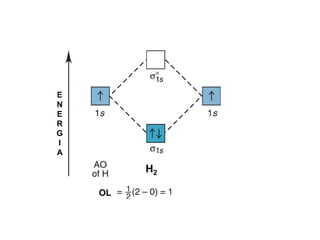
H2

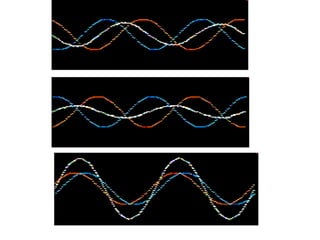
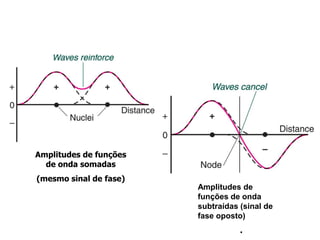
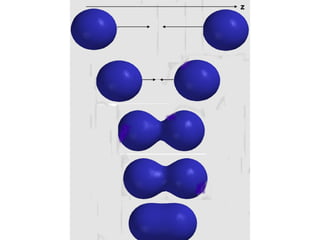
representação da interferência
construtiva que ocorre quando
dois orbitais H 1s se superpõe e
formam um orbital molecular
(1) 
1
2(1 S)
[A(1)  B(1)]

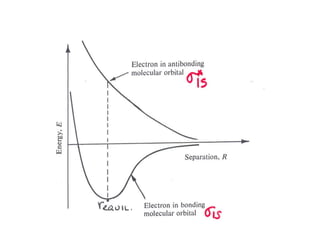
13. H2

representação da interferência
destrutiva que ocorre quando
dois orbitais H 1s se superpõe e
formam um orbital molecular
(1) 
1
2(1 S)
[A(1)  B(1)] Função de onda atômica, estado antiligante

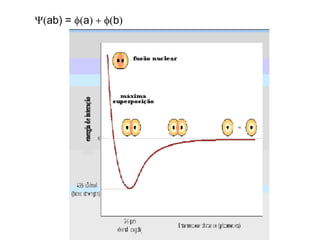
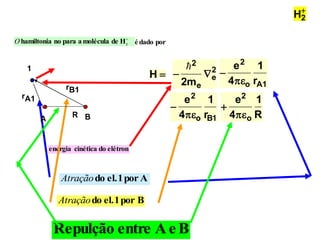
14. Em termos de energia
Y(ab) = f(a)  f(b)
Calcular para as duas situações
Usando:
Y(ab) = f(a)  [f(b)]

15. Y(ab) = f(a)  f(b)

18. Diagrama de energia para a molécula de H2

19. Diagrama de energia para a molécula de H2

20. OL = Ordem de ligação =
1/2( # e- ligantes – # e- antiligantes)
> Ordem de ligação = ligação mais forte
O que é energia de ligação?
Energia necessária para quebrar a ligação
(desfazer a molécula)
Quanto mais forte Maior a energia

21. OL
E
N
E
R
G
I
A
H2

22. s
s
1s
OA do H
1s
OA do H
OM do H2
-
OA do H OA do H
1s
s
s
1s
OM do H2
+
OL = ½ - 0 = ½ OL = 1 – 0,5 = ½

23. Helio: He2
OM do
He2
OA do
He
1s
OA do
He
1s
s*1s
s1s
Energia
He2 ordem de ligação = 0
Portanto....
NÃO EXISTE

24. Conf.
eletrônica
OL Energia
Ligação
Compr.
Ligação
H2
+ (s1s)1 ½ 255 1,06
H2 (s1s)2 1 431 0,74
He2 (s1s)2 (s*1s)2 0 0 não liga

27. Energia de Separação entre
Orbitais s-p

28. Ligações formadas pela superposição de 2 orbitais atômicos do tipo p formando orbitais s.
Orbitais moleculares formados a partir de orbitais atômicos do tipo s.

29. Ligações formadas pela superposição de 2 orbitais atômicos
do tipo p formando orbitais .

31. Eixo Z
Eixo x
ou
Eixo y

32. Estes orbitais não se superpõem apreciavelmente ou não se
superpõem de modo algum em virtude de não apresentarem
simetria e energia apropriadas.
Orbital Molecular não ligante

33. Orbital σ (Ligação σ)
Tipos de orbitais
Por convenção o eixo z é o eixo internuclear
Formado pela sobreposição de orbitais atômicos
que possuem simetria cilíndrica ao redor do eixo internuclear (z)
Os orbitais σ podem ser formados de várias maneiras:
sobreposição s,s
sobreposição s,p
sobreposição p,p

37. Energy
2s 2s
2sg
2su*
2p
2p
3sg
3su*
1u
1g*
Molecular Orbital Theory
(px,py)
pz
Diagrama de energia para
Li2 Be2 B2 C2 N2

38. Li2 Be2 B2 C2 N2O2 F2 Ne2