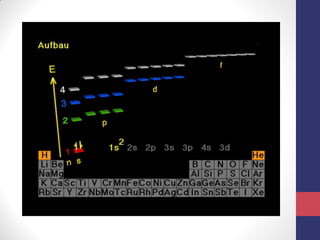
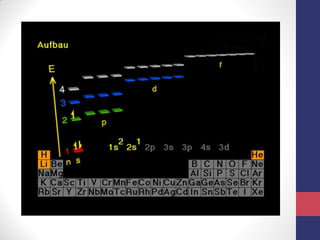
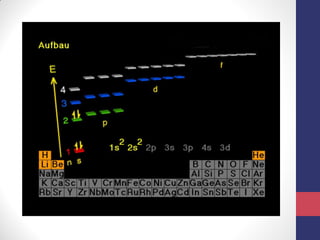
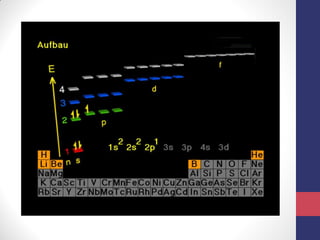
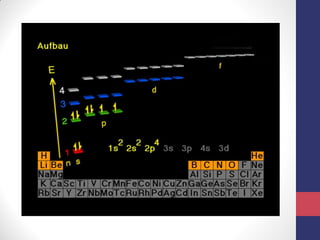
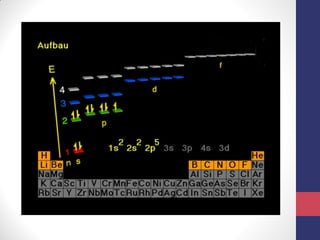
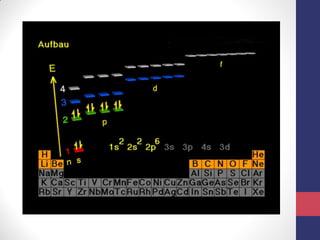
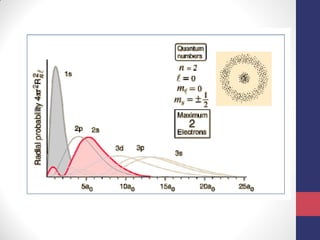
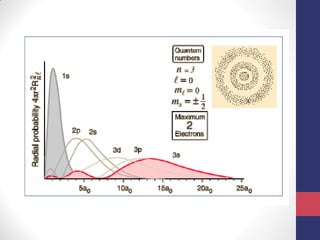
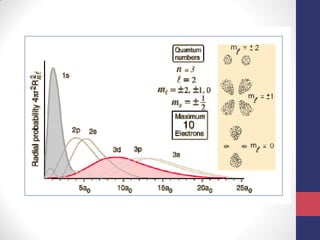
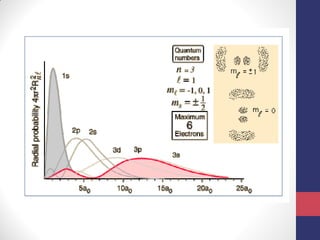
O documento discute os conceitos fundamentais da estrutura atômica segundo a mecânica quântica, incluindo:
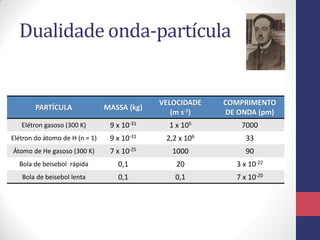
1) A dualidade onda-partícula e a equação de de Broglie que relaciona a massa e velocidade de uma partícula com seu comprimento de onda;
2) O princípio da incerteza de Heisenberg que estabelece limites na precisão com que podemos determinar simultaneamente a posição e momento de uma partícula;
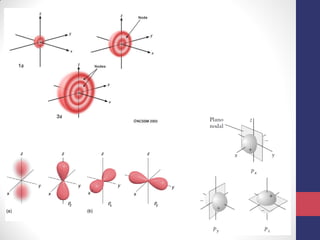
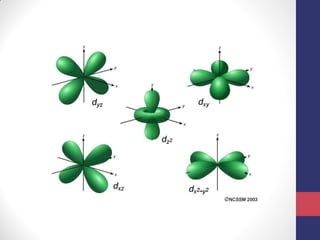
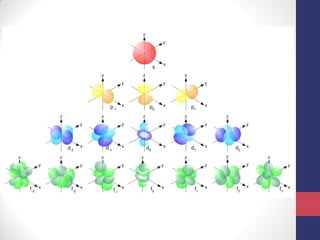
3) A equação de Schrödinger que descreve o comportamento das