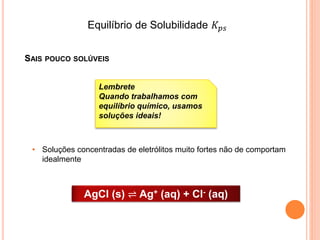
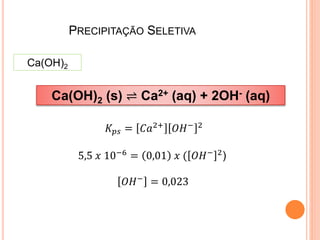
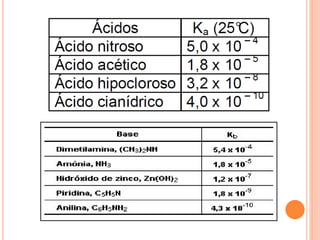
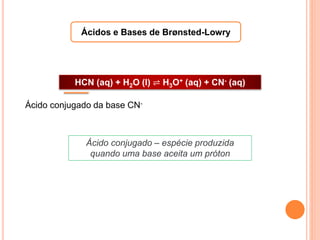
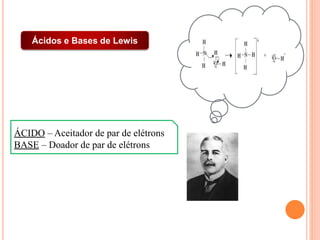
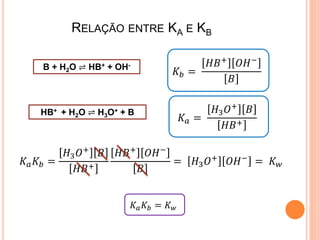
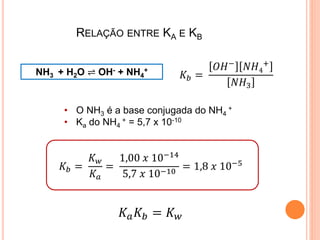
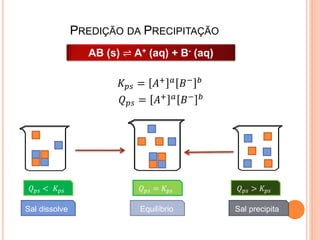
O documento discute equilíbrio químico em soluções aquosas, incluindo: 1) Equilíbrio de solubilidade de sais pouco solúveis e como a presença de íons comuns afeta a solubilidade. 2) Equilíbrio ácido-base, incluindo definições de ácidos e bases, constantes de acidade e basicidade (Ka, Kb, Kw), e relação entre pH e pOH. 3) Previsão da precipitação de sais com base nos valores de Kps e Qps.

1. EQUILÍBRIO QUÍMICO
SQM 0405 – Química Geral e Experimental: Teórica e Prática
Amanda Ribeiro Guimarães
amandaiqsc@iqsc.usp.br
quimicageralemais.blogspot.com.br

2. EQUILÍBRIO IÔNICO EM SOLUÇÃO AQUOSA
 Sais pouco solúveis
 Ácidos e bases
 Equilíbrio ácido-base
 Ka, Kb e Kw
 pH e pOH
 Solução Tampão

3. SAIS POUCO SOLÚVEIS
AgCl (s) ⇌ Ag+ (aq) + Cl- (aq)
• Soluções concentradas de eletrólitos muito fortes não de comportam
idealmente
Lembrete
Quando trabalhamos com
equilíbrio químico, usamos
soluções ideais!
Equilíbrio de Solubilidade 𝐾 𝑝𝑠

4. 𝐾 𝑝𝑠 = constante do produto de solubilidade
O produto de solubilidade é a constante de equilíbrio entre um
sal não-dissociado e seus íons em uma solução saturada.
AgCl (s) ⇌ Ag+ (aq) + Cl- (aq)
𝐾 𝑝𝑠 =[𝐴𝑔+][𝐶𝑙−]
Ag+
Cl-
AgCl (s)

5. SOLUBILIDADE
AgCl (s) ⇌ Ag+ (aq) + Cl- (aq)
𝐾 𝑝𝑠 = 1,8. 10−10
𝐾 𝑝𝑠 =[𝐴𝑔+
][𝐶𝑙−
]
AgCl (s) ⇌ Ag+ (aq) + Cl- (aq)
[𝐴𝑔+]= S [𝐶𝑙−] = S
S S
𝐾 𝑝𝑠 =𝑆. 𝑆
𝑆2
=1,8. 10−10 𝑆 =1,3. 10−5
M
Se encontrarmos a solubilidade das espécies encontramos o
número máximo de mols de AgCl que podem ser dissolvidos em 1L
de água.

6. 𝐂𝐚𝑭 𝟐(𝒔) ⇌ 𝑪𝒂 𝟐+(aq) + 𝟐𝑭−(aq)
𝐾 𝑝𝑠 = 3,9. 10−11
Exemplo
1) Calcular a solubilidade do Ca𝐹2(𝑠) em água.
S=2,1. 10−4

7. SOLUBILIDADE NA PRESENÇA DE ÍON COMUM
Qual a solubilidade do AgCl em uma solução 1,0 𝑥 10−2 𝑀 de AgNO3?
𝐾𝑝𝑠 = 𝐴𝑔+
𝐶𝑙−
𝐴𝑔+
= 𝐴𝑔+
𝑑𝑜 𝐴𝑔𝑁𝑂3
+ 𝐴𝑔+
𝑑𝑜 𝐴𝑔𝐶𝑙
1,0 𝑥 10−2 𝑀
1,3 𝑥 10−5
𝑀
Ag+ Cl-
AgCl (s)
𝐴𝑔+ = 1,3 𝑥 10−5
𝑀
AgCl (s) ⇌ Ag+ (aq) + Cl- (aq)
[𝐴𝑔+]= S [𝐶𝑙−] = S
𝑆 =1,3. 10−5M
𝑆 =1,3. 10−5M

8. SOLUBILIDADE NA PRESENÇA DE ÍON COMUM
𝐴𝑔+ = 𝐴𝑔+
𝑑𝑜 𝐴𝑔𝑁𝑂3
+ 𝐴𝑔+
𝑑𝑜 𝐴𝑔𝐶𝑙
1,0 𝑥 10−2
𝑀
< 1,3 𝑥 10−5 𝑀
𝐴𝑔+
≅ 1,0 𝑥 10−2
𝑀
𝐶𝑙− =
𝐾 𝑝𝑠
𝐴𝑔+
≅
1,8 𝑥 10−10
1,0 𝑥 10−2
= 1,8 𝑥 10−8 𝑀

9. SOLUBILIDADE NA PRESENÇA DE ÍON COMUM
S= 1,8 𝑥 10−8 𝑀
AgCl (s) ⇌ Ag+ (aq) + Cl- (aq)
S = 1,3 𝑥 10−5
𝑀
Em 𝐻2 𝑂
Em solução de AgNO3
A presença de um íon comum diminui a solubilidade

10. PREDIÇÃO DA PRECIPITAÇÃO
AB (s) ⇌ A+ (aq) + B- (aq)
𝐾𝑝𝑠 = 𝐴+ 𝑎
𝐵− 𝑏
𝑄 𝑝𝑠 < 𝐾 𝑝𝑠 𝑄 𝑝𝑠 = 𝐾 𝑝𝑠 𝑄 𝑝𝑠 > 𝐾 𝑝𝑠
Sal dissolve Equilíbrio Sal precipita
𝑄 𝑝𝑠 = 𝐴+ 𝑎
𝐵− 𝑏

11. PREDIÇÃO DA PRECIPITAÇÃO
Ocorrerá precipitação quando:
𝑸 𝒑𝒔 ≥ 𝑲 𝒑𝒔
Haverá formação de precipitado de PbI2 quando volumes iguais de
soluções 0,2 M de nitrato de chumbo (II) e iodeto de potássio são
misturadas?
Pb(NO3)2 (aq) + 2KI (aq) → 2KNO3 (aq) + PbI2 (s)
Pb2+ (aq) + 2I- (aq)→ PbI2 (s)
PbI2 (s) ⇌ Pb2+ (aq) + 2I- (aq)
𝐾 𝑝𝑠 = 𝑃𝑏2+ 𝐼− 2 = 1,4 𝑥 10−8

12. PREDIÇÃO DA PRECIPITAÇÃO
PbI2 (s) ⇌ Pb2+ (aq) + 2I- (aq) 𝐾 𝑝𝑠 = 𝑃𝑏2+
𝐼− 2
= 1,4 𝑥 10−8
• Volumes iguais de soluções 0,2 M de nitrato de chumbo (II) e
iodeto de potássio são misturadas.
• O volume final será duas vezes maior, logo as novas
molaridades serão: 0,1 M em Pb2+ (aq) e 0,1 M em I- (aq):
𝑄 𝑝𝑠 = 𝑃𝑏2+ 𝐼− 2 = 0,1 𝑥(0,1)2= 1 𝑥 10−3
𝑄 𝑝𝑠 > 𝐾 𝑝𝑠 Haverá precipitação!

13. PRECIPITAÇÃO SELETIVA
Uma amostra de água do mar contém, entre outros solutos,
as seguintes concentrações de cátions solúveis: 0,050 M de
Mg2+ (aq) e 0,010 M de Ca2+ (aq) . Determine a ordem com
que cada íon precipita com a adição progressiva de NaOH
sólido. Dê a concentração de OH- quando a precipitação de
cada um deles começar e suponha que não há mudança de
volume com a adição de NaOH.
Ca(OH)2 Mg(OH)2
𝐾 𝑝𝑠 = 5,5 𝑥 10−6
𝐾 𝑝𝑠 = 1,1 𝑥 10−11

14. PRECIPITAÇÃO SELETIVA
Ca(OH)2
Ca(OH)2 (s) ⇌ Ca2+ (aq) + 2OH- (aq)
𝐾𝑝𝑠 = 𝐶𝑎2+ 𝑂𝐻− 2
5,5 𝑥 10−6
= 0,01 𝑥 ( 𝑂𝐻− 2
)
𝑂𝐻−
= 0,023

15. PRECIPITAÇÃO SELETIVA
Mg(OH)2
Mg(OH)2 (s) ⇌ Mg2+ (aq) + 2OH- (aq)
𝐾𝑝𝑠 = 𝑀𝑔2+ 𝑂𝐻− 2
1,1 𝑥 10−11
= 0,05 𝑥 ( 𝑂𝐻− 2
)
𝑂𝐻−
= 1,5 𝑥 10−5

16. PRECIPITAÇÃO SELETIVA
Mg(OH)2 𝑂𝐻−
= 1,5 𝑥 10−5
𝑀
Ca(OH)2 𝑂𝐻−
= 0,023 𝑀
Portanto, os hidróxidos precipitam na ordem Mg(OH)2, em
1,5 x 10-5 M OH-(aq) e Ca(OH)2, em 0,023 M OH-(aq).

17. EQUILÍBRIO ÁCIDO-BASE
 Ácidos e bases
 Conceitos
 Equilíbrio ácido-base
 Ka, Kb e Kw
 pH e pOH

18. ÁCIDOS E BASES: CONCEITOS
Ácidos e Bases de Arrhenius
ÁCIDO – SE DISSOCIA LIBERANDO H+
BASE – SE DISSOCIA LIBERANDO OH-
HCl (g) + NH3 (l) → NH4
+ + Cl-
BASE
Oi???

19. ÁCIDOS E BASES: CONCEITOS
Ácidos e Bases de Brønsted-Lowry
ÁCIDO – DOADOR DE PRÓTONS
BASE – ACEITADOR DE PRÓTONS
HCl (aq) + H2O (l) → H3O+ (aq) + Cl- (aq)
O próton é transferido do ácido para a base!
H+ não existe
isoladamente em água!

20. Ácidos e Bases de Brønsted-Lowry
HCl (aq) + H2O (l) → H3O+ (aq) + Cl- (aq)
HCN (aq) + H2O (l) ⇌ H3O+ (aq) + CN- (aq)
ÁCIDO FORTE – completamente desprotonado em solução
ÁCIDO FRACO – parcialmente desprotonado em solução
A força do ácido depende do solvente!

21. Ácidos e Bases de Brønsted-Lowry
O2
- (aq) + H2O (l) → 2 OH- (aq)
NH3 (aq) + H2O (l) ⇌ NH4
+ (aq) + OH- (aq)
BASE FORTE – completamente protonada em solução
BASE FRACA – parcialmente protonado em solução
A força da base depende do solvente!

22. Ácidos e Bases de Brønsted-Lowry
HCN (aq) + H2O (l) ⇌ H3O+ (aq) + CN- (aq)
Base conjugada do ácido HCN
Base conjugada – espécie produzida
quando um ácido doa um próton

23. Ácidos e Bases de Brønsted-Lowry
HCN (aq) + H2O (l) ⇌ H3O+ (aq) + CN- (aq)
Ácido conjugado da base CN-
Ácido conjugado – espécie produzida
quando uma base aceita um próton

24. Ácidos e Bases de Lewis
ÁCIDO – Aceitador de par de elétrons
BASE – Doador de par de elétrons

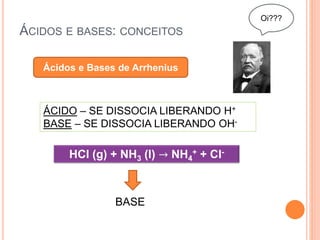
25. CONSTANTES DE ACIDEZ E BASICIDADE
𝐻𝐴 + 𝐻2 𝑂 ⇄ 𝐻3 𝑂+
+ 𝐴−
𝐾𝑎=
𝐻3 𝑂+ [𝐴 −
]
[𝐻𝐴]
B + 𝐻2 𝑂 ⇄ 𝐻𝐵+
+ 𝑂𝐻 −
𝐾𝑏=
𝐻𝐵+ [𝑂𝐻 −
]
[𝐵]
Uma base
abstrairá os
prótons de
qualquer ácido,
inclusive a água.
A maneira de compararmos a
força de um ácido é por meio de
sua tendência em transferir um
próton para uma mesma base,
geralmente a água.

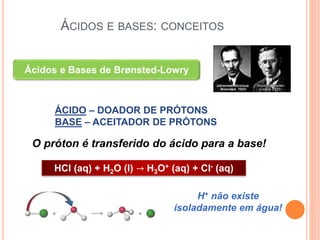
26. A ESCALA DE PH
pH = -log [H3O+] pOH = -log [OH-]
• Para a água pura, a molaridade dos íons H3O+ é
1,0 𝑥 10−7 𝑚𝑜𝑙 𝐿−1, em 25°C. Seu pH será:
pH = -log [H3O+] = -log (1,0 x 10-7) = 7,0

27. A AUTO-IONIZAÇÃO DA ÁGUA
2 H2O ⇌ H3O+ + OH-
𝐾 𝑤 = 𝐻3 𝑂+
𝑂𝐻−
CONSTANTE DO PRODUTO IÔNICO DA ÁGUA- Kw
Kw = 1,00 x 10-14, a 25°C
pKw = -log Kw = -log (1,00 x 10-14) = 14,00

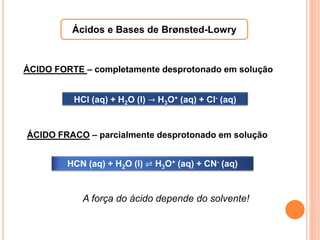
28. A AUTO-IONIZAÇÃO DA ÁGUA
2 H2O ⇌ H3O+ + OH-
CONSTANTE DO PRODUTO IÔNICO DA ÁGUA- Kw
Solução neutra a 25°C:
[H3O+] = [OH-] = 1,00 x 10-7 M
pH = pOH = 7,00
pH + pOH = pKw = 14,00

29. RELAÇÃO ENTRE KA E KB
𝐾𝑎 =
𝐻3 𝑂+ 𝐵
𝐻𝐵+
HB+ + H2O ⇌ H3O+ + B
𝐾𝑏 =
𝐻𝐵+ 𝑂𝐻−
𝐵
𝐾𝑎 𝐾𝑏 =
𝐻3 𝑂+
𝐵
𝐻𝐵+
𝐻𝐵+
𝑂𝐻−
𝐵
= 𝐻3 𝑂+
𝑂𝐻−
= 𝐾 𝑤
B + H2O ⇌ HB+ + OH-
𝐾𝑎 𝐾𝑏 = 𝐾 𝑤

30. RELAÇÃO ENTRE KA E KB
NH3 + H2O ⇌ OH- + NH4
+
𝐾𝑏 =
𝑂𝐻−
𝑁𝐻4
+
𝑁𝐻3
𝐾𝑏 =
𝐾 𝑤
𝐾𝑎
=
1,00 𝑥 10−14
5,7 𝑥 10−10
= 1,8 𝑥 10−5
𝐾 𝑎 𝐾𝑏 = 𝐾 𝑤
• O NH3 é a base conjugada do NH4
+
• Ka do NH4
+ = 5,7 x 10-10

31. 1) 𝐾 𝑎 mede a capacidade de doação de prótons de um ácido
2) 𝐾𝑏 mede a capacidade de aceitação de prótons de uma base
Um 𝐾 𝑎 pequeno (um 𝑝 𝑘𝑎 grande) significa que o ácido doa poucos prótons.
 Quanto maior for o valor de 𝑝 𝑘𝑎 menor será o 𝐾 𝑎
e mais fraco é o ácido.
 Quanto maior for o valor de 𝑝 𝑘𝑏 menor será o 𝐾𝑏
e mais fraco é a base.
Kw = 1,00 x 10-14, a 25°C
pKw = -log Kw= 14,00

32. EXEMPLOS
SOLUÇÕES DE ÁCIDOS FRACOS
1) Calcular o pH e a percentagem de desprotonação de
0,10 M CH3COOH (aq) sabendo que a constante Ka do
ácido acético é 1,8 x 10-5.
CH3COOH (aq) + H2O (l) ⇌ H3O+ (aq) + CH3CO2
- (aq)
Percentagem de desprotonação=
𝑀𝑜𝑙𝑎𝑟𝑖𝑑𝑎𝑑𝑒 𝑑𝑒𝐴−
𝑚𝑜𝑙𝑎𝑟𝑖𝑑𝑎𝑑𝑒 𝑖𝑛𝑖𝑐𝑖𝑎𝑙𝑑𝑒 𝐻𝐴
𝑋 100%

33. EXEMPLOS
SOLUÇÕES DE BASES FRACAS
2) Calcular o pH e a percentagem de protonação de uma
solução 0,20 M de metilamina, CH3NH2, em água. A
constante Kb da CH3NH2 é 3,6 x 10-4.
CH3NH2 (aq) + H2O (l) ⇌ CH3NH3
+ (aq) + OH- (aq)

34. SOLUÇÃO TAMPÃO
 TAMPÃO ÁCIDO
 Ácido fraco + base conjugada na forma de sal
 TAMPÃO BÁSICO
 Base fraca + ácido conjugado na forma de sal
Estabiliza o pH de soluções em água!

35. TAMPÃO ÁCIDO
CH3COOH (aq) + H2O (l) ⇌ H3O+ (aq) + CH3CO2
- (aq)
• Ácido fraco + base conjugada na forma de sal
• Estabiliza soluções com pH < 7
Adicionando ácido forte a uma solução com concentrações
aproximadamente iguais de CH3COOH e CH3CO2
- :
Os íons H3O+ adicionados transferem prótons para
os íons CH3CO2
- para produzir CH3COOH e H2O. O
pH se mantém quase inalterado pois os íons hidrônio
adicionados são removidos pelos íons acetato.

36. TAMPÃO BÁSICO
NH3 (aq) + H2O (l) ⇌ NH4
+ (aq) + OH- (aq)
• Base fraca + ácido conjugado na forma de sal
• Estabiliza soluções com pH > 7
Adicionando base forte a uma solução com concentrações
aproximadamente iguais de NH3 e NH4
+:
Os íons OH- removem prótons dos íons NH4
+ para
produzir NH3 e H2O. O pH se mantém quase inalterado
pois os íons hidroxila adicionados são removidos pelos
íons amônio.

37. CÁLCULO DO PH DE UMA SOLUÇÃO TAMPÃO
Calcule o pH de uma solução tampão 0,040 M NaCH3CO2 (aq) e
0,080 M CH3COOH (aq) em 25°C.
CH3COOH (aq) + H2O (l) ⇌ H3O+ (aq) + CH3CO2
- (aq)
𝐾 𝑎 =
𝐻3 𝑂+ 𝐶𝐻3 𝐶𝑂2
−
𝐶𝐻3 𝐶𝑂𝑂𝐻
= 1,8 𝑥 10−5
𝐻3 𝑂+ = 𝐾 𝑎 𝑥
𝐶𝐻3 𝐶𝑂𝑂𝐻
𝐶𝐻3 𝐶𝑂2
− = 1,8 𝑥 10−5 𝑥
0,080
0,040
= 3,6 𝑥 10−5
𝑝𝐻 = − log 3,6 𝑥 10−5
= 4,44

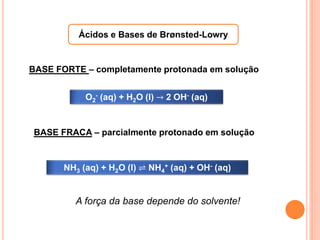
38. EQUAÇÃO DE HENDERSON-HASSELBALCH
𝑝𝐻 = 𝑝𝐾 𝑎 + 𝑙𝑜𝑔
[𝑏á𝑠𝑖𝑐𝑜]𝑖𝑛𝑖𝑐𝑖𝑎𝑙
[á𝑐𝑖𝑑𝑜]𝑖𝑛𝑖𝑐𝑖𝑎𝑙

39. EXEMPLOS
SOLUÇÃO TAMPÃO
3) Suponha que dissolvemos 1,2 g de hidróxido de sódio
(0,030 mol NaOH) em 500 mL da solução tampão
descrita anteriormente. Calcule o pH da solução
resultante e a mudança de pH. Considere que o volume
da solução não se alterou.
CH3COOH (aq) + H2O (l) ⇌ H3O+ (aq) + CH3CO2
- (aq)
pH=5,44