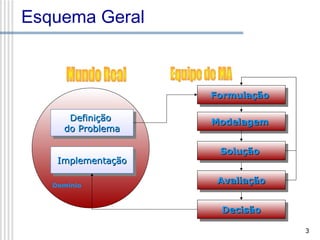
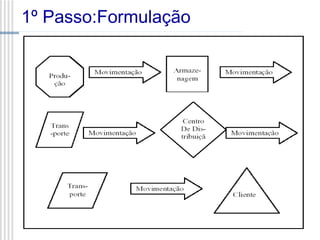
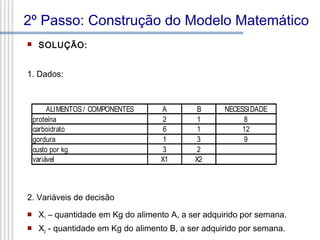
Este documento descreve os principais passos da modelagem ambiental para resolver um problema: 1) formulação do problema, 2) construção de um modelo matemático, 3) solução do modelo, 4) avaliação do modelo e da solução, 5) tomada de decisão e 6) implementação. O documento explica cada um destes passos em detalhe e fornece um exemplo de como modelar matematicamente um problema de dieta para ilustrar o processo.

1. MODELAGEM AMBIENTAL
Prof. Rui Souto de Alencar Filho

2. I. Introdução
 Os
principais passos na Modelagem
Ambiental para a resolução de um problema:
 formulação,
 modelação,
 resolução,
 avaliação,
 decisão,
 implementação.

Esquema Geral. Exemplos.
2

3. Esquema Geral
Formulação
Formulação
Definição
Definição
do Problema
do Problema
Implementação
Implementação
Domínio
Modelagem
Modelagem
Solução
Solução
Avaliação
Avaliação
Decisão
Decisão
3

4. 1º Passo: Formulação
Quando
se pode dizer que uma pessoa ou um
grupo tem um problema?
1º
- Se existir a necessidade de atingir um ou
mais de um resultado;
2º Se há uma ou mais linhas de ação capazes
de levar aos objetivos desejados com eficiência
diferentes; e
3º Se há dúvidas sobre qual melhor linha de
ação.
4

5. 1º Passo: Formulação

Exemplo de um problema complexo:
A escolha da embalagem dentro da cadeia logística.
Querem
atingir um ou mais resultados: Com a
escolha da embalagem certa, o administrador da
cadeia logística espera obter um resultado positivo
no processo logístico;
Têm
diante de si uma ou mais linhas de ação que
atingem os objetivos desejados com eficiências
diversas: As múltiplas opções para a escolha das
embalagens expressam tais linhas de ação, de modo
que a eficiência do processo logístico se revela maior ou
menor de acordo com as diferenças apuradas nos custos
5
relativos à opção adotada.

6. 1º Passo: Formulação
Têm
dúvidas sobre qual é a “melhor” linha de
ação: Nosso problema central é representado aqui
pela necessidade de adoção de parâmetros que orientem a
escolha da embalagem que produza o melhor resultado
possível.
6

7. 1º Passo: Formulação
Os
aspectos que devem ser examinados para formular um
problema são:
1º - Quem toma a decisão e quais são os seus objetivos;
2º - Quais são as variáveis controladas e dentro de que
limites elas podem ser controladas (restrições);
3º - Quais as variáveis não controladas (outros aspectos do
meio ambiente que envolvem ou não seres humanos que
podem afetar o resultado).
7

8. 1º Passo: Formulação
4º
- O problema deve ser analisado a partir de um
sistema integrado, onde interagem várias componentes,
todas elas interdependentes, para o qual é preciso obter
uma solução ótima que satisfaça a todas elas.
A análise de sistemas é a maneira mais
eficiente de descobrir como o sistema realmente
opera, porque proporciona informações básicas
necessárias à formulação do problema e acerca
do modelo próprio à solução mais adequada.
É muito difícil procurar uma solução “certa”
para um problema mal formulado !!!
8

9. 1º Passo: Formulação
Quem
toma a decisão: Quando no papel
de tomador de decisão, o administrador
da cadeia logística deve traçar os
objetivos que devem ser alcançados
com a resolução do problema.
Quanto
aos objetivos:
9

10. 1º Passo:Formulação
 variáveis controladas: Quais variáveis da situação
estão sujeitos ao controle de quem toma a decisão
Variáveis Controladas
Tipo de Embalagens
Disponibilidade financeira
Restrições
Características do Produto
Características Físicas do
Meio de Distribuição
as restrições (limitações): existentes no sistema
em
geral,
definidas
pelas
relações
de
interdependências
entre
as componentes
10

11. 1º Passo:Formulação

variáveis não controladas:
Intempéries Ambientais
Variáveis Não
Controladas
Fragilidade do Produto
Satisfação do Cliente
11

12. 1º Passo:Formulação

A teoria de Pesquisa Operacional na
modelagem ambiental sobre a formulação do
problema dá ênfase à análise do sistema
como o meio de melhor compreender o
assunto.

Em Logística, a importância da análise
sistêmica se mostra nos conceitos de
Logística Integrada e Custo Total Logístico.
12

13. 1º Passo:Formulação
13

14. 2º Passo: Construção do Modelo Matemático.
O que é um modelo ?
Um modelo é uma representação simplificada de
Um modelo é uma representação simplificada de
uma situação da vida real.
uma situação da vida real.
Um modelo reflete a essência do problema,
Um modelo reflete a essência do problema,
representando as relações de interdependência
representando as relações de interdependência
existentes entre todas as componentes da
existentes entre todas as componentes da
situação em estudo.
situação em estudo.
14

15. Modelo Matemático
O que é um modelo matemático?
Um modelo matemático é uma representação
Um modelo matemático é uma representação
simplificada de uma situação da vida real,
simplificada de uma situação da vida real,
formalizado
com
símbolos
e
expressões
formalizado
com
símbolos
e
expressões
matemáticas.
matemáticas.
Um exemplo da Física: F = m a
Um exemplo da Física: F = m a
A modelagem matemática de um problema
possibilita uma melhor compreensão da essência
do mesmo !!!
15

16. Modelo Matemático

Os modelos matemáticos em que todas as
informações relevantes são assumidas
como conhecidas (sem incertezas) são
chamados de determinísticos.

Os modelos em que uma ou mais variáveis
de decisão não sejam conhecidas, devendo
esta incerteza ser incorporada no modelo,
são chamados de modelos probabilísticos
ou estocásticos.
16

17. Modelo Matemático de um Problema de Otimização
modelo matemático de um Problema de
Otimização é definido por:
Um

um número N de decisões
denominadas variáveis de decisão,
a
ser
tomadas,

uma função matemática, que representa a medida da
vantagem ( desvantagem ) da tomada de decisão
denominada função objetivo,

um conjunto de restrições associadas às variáveis de
decisão denominadas restrições do modelo,

um conjunto de constantes (coeficientes) da função
objetivo e das restrições denominadas parâmetros do
17
modelo.

18. Aspectos fundamentais a ter em conta durante a modelagem .
1.

Simplificar sem perder a essência do problema.
 CUIDADO
!!!: a simplificação do modelo deve
corresponder à realidade, de tal forma que as soluções
obtidas através do modelo matemático possam
realmente ser aplicadas na vida real.
2. Processo em espiral
 O processo de modelagem desenvolve-se em forma de
espiral, começando por uma representação simplificada
do problema, até se chegar depois de vários ciclos a
uma representação mais próxima da situação em estudo
na vida real.
 Um problema pode ser reformulado se:
 Durante a etapa da avaliação os resultados demonstram que
é preciso uma reformulação do problema incorporando novas
restrições, alterando os valores de alguns dos parâmetros,
etc..
 Depois de avaliadas e implementadas as soluções, pretendese agora avançar para uma etapa mais complexa de
resolução.
18

19. Aspectos fundamentais a ter em conta durante a modelagem
2.
Processo em espiral
 Este processo de reformulação e remodelação pode
repetir-se, até que o modelo desenvolvido e as suas
soluções representem, o mais fielmente possível, a
complexidade do problema em estudo, e as soluções
implementadas
satisfaçam
completamente
os
principais objetivos traçados.
3. Escolha do modelo certo
 Na maioria das situações, o problema pode ser
representado por modelos e problemas tipo
já
desenvolvidos pela PO.
Neste caso formular
matematicamente o problema não é mais do que
convertê-lo em certos modelos e problemas tipo da
PO (modelos de Programação Linear, Programação
19
Dinâmica, Problema de Transporte, etc.)

20. 2º Passo: Construção do Modelo Matemático.
A PO estrutura e formula um problema de
otimização da vida real dentro de um modelo
matemático
que
reflete
a
essência
do
problema, de forma que as decisões (soluções)
obtidas, possam ser aplicadas na situação real.
20

21. 2º Passo: Construção do Modelo Matemático.
Exemplo: Problema da Dieta:

Suponhamos que 8, 12 e 9 unidades de
proteínas,
carboidratos
e
gorduras,
respectivamente,
sejam
as
necessidades
semanais mínimas para cada pessoa. O alimento
A (macarronada) contém por quilo 2, 6 e 1
unidade de proteínas, carboidratos e gorduras, e
o alimento B (feijoada) contém por quilo 1, 1 e 3
unidades respectivamente. Se A custa 3
unidades monetárias (u.m.) e B custa 2 u.m.,
quantos quilos de cada um deve-se comprar por
semana para ter a dieta de menor custo?

22. 2º Passo: Construção do Modelo Matemático

SOLUÇÃO:
1. Dados:
ALIMENTOS / COMPONENTES
proteína
carboidrato
gordura
custo por kg
variável
A
2
6
1
3
X1
B
1
1
3
2
X2
NECESSIDADE
8
12
9
2. Variáveis de decisão

X1 – quantidade em Kg do alimento A, a ser adquirido por semana.

X2 - quantidade em Kg do alimento B, a ser adquirido por semana.

23. 2º Passo: Construção do Modelo Matemático
3. Objetivo
Deve-se determinar os valores da variáveis de decisão de modo a
minimizar o custo.
Custo do alimento A = 3.X1 (3 U.M. vezes a quantidade de A em quilo)
Custo
Z
do alimento B = 2.X2 (2 U.M. vezes a quantidade de B em quilo)
= 3.X1 + 2. X2 (Função Objetivo)
4. Restrições
2X1 + X2 >= 8 (necessidade de proteínas)
6X1 + X2 >= 12 (nec. carboidrato)
X1 + 3X2 >= 9 (nec. gordura)
X1 >= 0; X2 >= 0

24. 2º Passo: Construção do Modelo Matemático

MODELO

Minimizar Z = 3.X1 + 2. X2

Sujeito a:
2X1 + X2 >= 8
6X1 + X2 >= 12
X1 + 3X2 >= 9
X1 >= 0; X2 >= 0

25. 3º Passo: Solução do Modelo
Resolver um modelo é achar uma solução
(valores para as variáveis de decisão)
que não viole as restrições e que otimize
(max ou mim) a função objetivo.
25

26. 3º Passo: Solução do Modelo
Ao contrário das outras fases, que não
possuem regras fixas, a solução do modelo
é baseada geralmente em técnicas
matemáticas existentes.
A solução é obtida pelo algoritmo mais
adequado, em termos de rapidez de
processamento e precisão da resposta. Isto
exige um conhecimento profundo das
principais técnicas existentes. A solução
obtido, neste caso, é dita "ótima".
26

27. 3º Passo: Solução do Modelo
Um algoritmo é uma sequência finita e não
ambígua de instruções computáveis para
solucionar um problema
27

28. 3º Passo: Solução do Modelo
Nesta fase pode ser utilizado muito dos
softwares e pacotes de computação
disponíveis
para a resolução de
problemas de Modelagem.
28

29. 4º Passo: Avaliação (Testar o Modelo e a
Solução)
Neste passo serão avaliados, tanto o modelo
escolhido, quanto as soluções obtidas, ou seja:
As soluções obtidas aderem à realidade?
Tais soluções são confiáveis para que
decisões baseadas nelas sejam tomadas?
Como a solução ótima reage à análise de
sensibilidade sobre os parâmetros?
29

30. 4º Passo: Avaliação (Testar o Modelo e a
Solução)
Análise de Sensibilidade:
A
análise de sensibilidade é a parte da análise
estatística usada para avaliar qual o grau de
confiança dos resultados em situações de
decisões incertas ou suposições sobre os dados
e resultados usados
Utilizada
para decidir quais dados estimados
devem ser refinados antes de tomar uma
decisão
30

31. 4º Passo: Avaliação (Testar o Modelo e a Solução)
Dependendo das conclusões da avaliação, será
determinado o passo a seguir:
Se a avaliação é satisfatória:
proceder à tomada de decisão, que prepara as condições
para a implementação da solução obtida na situação real;
Se a avaliação é não satisfatória :
proceder à reformulação, remodelação e resolução do novo
modelo, a partir dos resultados obtidos no processo de
avaliação e também na análise de pós-otimização.
31

32. 5º Passo: Tomada de Decisão

Uma vez concluída satisfatoriamente a
etapa de avaliação, é preciso elaborar um
relatório bem documentado que possibilite a
implementação da situação obtida na
situação real.

Este relatório deve incluir:
o
modelo escolhido
 uma metodologia bem detalhada com
todos
os
passos
que
sejam
necessários
seguir
para
a
implementação da solução obtida.
32

33. 6º Passo: Implementação
A apresentação da solução deve ser
feita à administração da empresa
evitando-se o uso da linguagem técnica
do modelo.
Neste passo efetua-se a implementação
das
soluções obtidas usando a
metodologia elaborada. No processo de
implementação
é
preciso
envolver
ativamente a administração e todas as
componentes da organização que atuam
no sistema em estudo.
33

34. 6º Passo: Implementação
É conveniente que esta fase seja acompanhada
pela equipe responsável, tendo em vista que:
quando a implementação da solução é
colocada em prática, pode levar a possível
reformulação do modelo em alguma de suas
partes;

A
presença da equipe permite, também,
superar mais facilmente as resistências e
oposições às alterações propostas na
sistemática das operações.
34