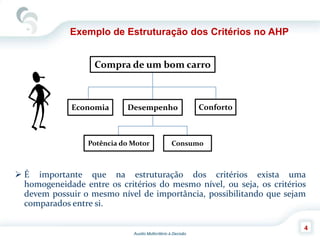
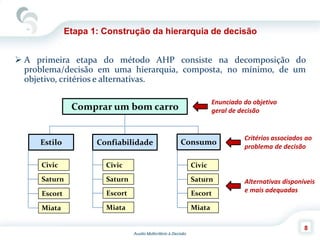
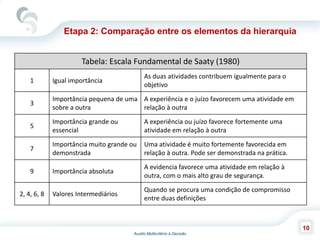
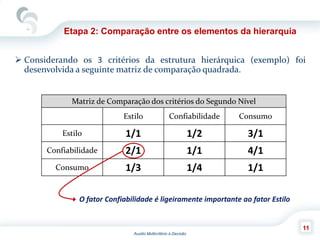
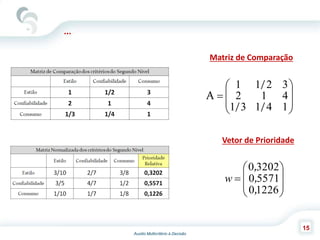
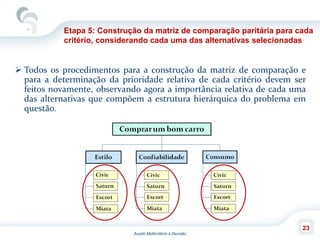
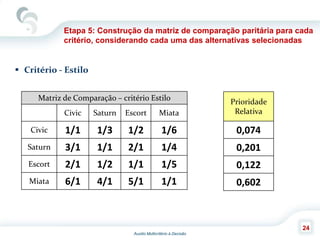
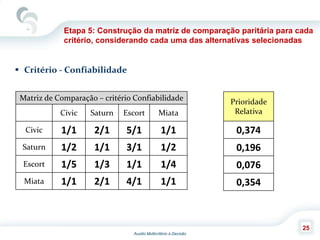
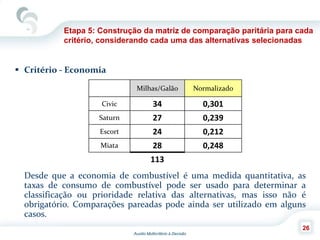
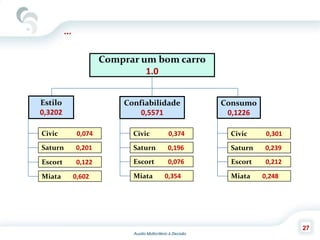
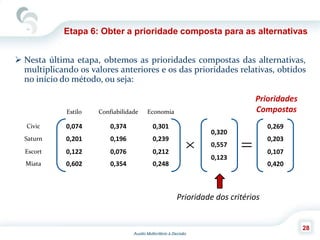
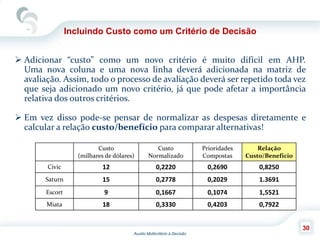
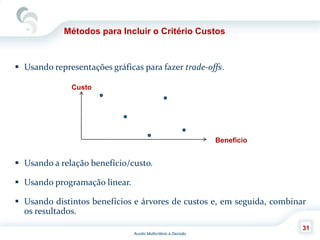
O documento descreve o Método de Análise Hierárquica (AHP), criado por Thomas Saaty em 1980, para auxiliar na tomada de decisões envolvendo múltiplos critérios. O AHP permite a decomposição de um problema de decisão em uma hierarquia com objetivo, critérios e alternativas, além de comparar os elementos por meio de uma escala fundamental. As principais etapas incluem a construção da hierarquia, comparação dos elementos, cálculo das prioridades relativas e avaliação da consistência dos julgamentos