O documento apresenta conceitos básicos sobre primitivas (ou antiderivadas). Em três frases ou menos, resume-se: O texto define primitiva como a função cuja derivada é igual a outra função em um intervalo. Apresenta teoremas sobre propriedades e cálculo de primitivas, incluindo que toda primitiva particular de uma função pode ser expressa como essa primitiva mais uma constante.

1. Aula 1 -
Primitivas
Willian Vieira
de Paula
Primitivas (ou
Anti-
Derivadas)
Antidiferencia¸˜o
ca
Defini¸˜o
ca
Propriedades Uma fun¸˜o F ser´ chamada de primitiva ou antiderivada de
ca a
uma fun¸˜o f num intervalo I se F (x) = f (x), para todo
ca
x ∈ I.

2. Aula 1 -
Primitivas
Willian Vieira
de Paula
Teorema
Primitivas (ou
Anti- Se F e G forem duas fun¸˜es, tais que F (x) = G (x), para
co
Derivadas)
todo x no intervalo I , ent˜o haver´ uma constante K , tal que
a a
Antidiferencia¸˜o
ca
F (x) = G (x) + K , para todo x em I .
Propriedades

3. Aula 1 -
Primitivas
Willian Vieira
de Paula
Teorema
Primitivas (ou
Anti- Se F e G forem duas fun¸˜es, tais que F (x) = G (x), para
co
Derivadas)
todo x no intervalo I , ent˜o haver´ uma constante K , tal que
a a
Antidiferencia¸˜o
ca
F (x) = G (x) + K , para todo x em I .
Propriedades
Teorema
Se F for uma primitiva particular de f em um intervalo I , ent˜o
a
toda primitiva de f em I ser´ dada por
a
F (x) + C .

4. Aula 1 -
Primitivas
Willian Vieira
de Paula
Primitivas (ou
Anti-
Defini¸˜o
ca
Derivadas)
Antidiferencia¸˜o ´ o processo de encontrar o conjunto de
ca e
Antidiferencia¸˜o
ca
todas as antiderivadas de uma fun¸˜o.
ca
Propriedades

5. Aula 1 -
Primitivas
Willian Vieira
de Paula
Primitivas (ou
Anti-
Defini¸˜o
ca
Derivadas)
Antidiferencia¸˜o ´ o processo de encontrar o conjunto de
ca e
Antidiferencia¸˜o
ca
todas as antiderivadas de uma fun¸˜o.
ca
Propriedades
Nota¸˜o:
ca
f (x)dx = F (x) + C

6. Aula 1 -
Primitivas
Willian Vieira
de Paula Propriedades
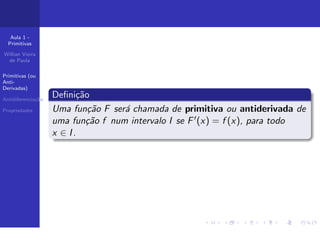
Primitivas (ou
Anti-
dx = x + C
Derivadas)
af (x)dx = a f (x)dx, onde a ´ uma constante.
e
Antidiferencia¸˜o
ca
Propriedades
Se f1 e f2 est˜o definidas no mesmo intervalo, ent˜o:
a a
[f1 (x) + f2 (x)] dx = f1 (x)dx + f2 (x)dx
Se n for um n´mero racional, n = 1, ent˜o:
u a
x n+1
x n dx = +C
n+1

7. Aula 1 -
Primitivas
Teoremas
Willian Vieira
de Paula
senxdx =
Primitivas (ou
Anti-
Derivadas)
cosxdx =
Antidiferencia¸˜o
ca
Propriedades
sec 2 xdx =
cosec 2 xdx =
secxtgxdx =
cosecxcotgxdx =

8. Aula 1 -
Primitivas
Teoremas
Willian Vieira
de Paula
senxdx = −cosx + C
Primitivas (ou
Anti-
Derivadas)
cosxdx = senx + C
Antidiferencia¸˜o
ca
Propriedades
sec 2 xdx = tgx + C
cosec 2 xdx = −cotgx + C
secxtgxdx = secx + C
cosecxcotgxdx = −cosecx + C