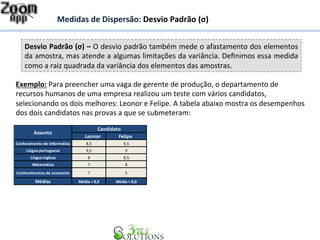
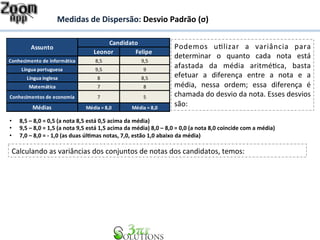
O documento discute medidas de dispersão de dados estatísticos, especificamente a variância e o desvio padrão. Explica como calcular o desvio padrão de um conjunto de notas de candidatos para determinar qual candidato teve as notas menos dispersas em relação à média, caso a média das notas seja igual entre os candidatos.

1. Esta%s&ca:

2. Esta%s&ca:
1. Introdução
à
Esta1s2ca;
2. Conceitos;
3. Medidas
Centrais;
4. Medidas
de
Dispersão:
a. Conceito;
b. Desvio
Médio
Absoluto;
c. Variância;
d. Desvio
Padrão.

3. Medidas
de
Dispersão:
Desvio
Padrão
(σ)
Desvio
Padrão
(σ)
–
O
desvio
padrão
também
mede
o
afastamento
dos
elementos
da
amostra,
mas
atende
a
algumas
limitações
da
variância.
Definimos
essa
medida
como
a
raiz
quadrada
da
variância
dos
elementos
das
amostras.

4. Medidas
de
Dispersão:
Desvio
Padrão
(σ)
Desvio
Padrão
(σ)
–
O
desvio
padrão
também
mede
o
afastamento
dos
elementos
da
amostra,
mas
atende
a
algumas
limitações
da
variância.
Definimos
essa
medida
como
a
raiz
quadrada
da
variância
dos
elementos
das
amostras.
Exemplo:
Para
preencher
uma
vaga
de
gerente
de
produção,
o
departamento
de
recursos
humanos
de
uma
empresa
realizou
um
teste
com
vários
candidatos,
selecionando
os
dois
melhores:
Leonor
e
Felipe.
A
tabela
abaixo
mostra
os
desempenhos
dos
dois
candidatos
nas
provas
a
que
se
submeteram:

5. Medidas
de
Dispersão:
Desvio
Padrão
(σ)
Desvio
Padrão
(σ)
–
O
desvio
padrão
também
mede
o
afastamento
dos
elementos
da
amostra,
mas
atende
a
algumas
limitações
da
variância.
Definimos
essa
medida
como
a
raiz
quadrada
da
variância
dos
elementos
das
amostras.
Exemplo:
Para
preencher
uma
vaga
de
gerente
de
produção,
o
departamento
de
recursos
humanos
de
uma
empresa
realizou
um
teste
com
vários
candidatos,
selecionando
os
dois
melhores:
Leonor
e
Felipe.
A
tabela
abaixo
mostra
os
desempenhos
dos
dois
candidatos
nas
provas
a
que
se
submeteram:
Candidato
Leonor Felipe
Conhecimento
de
informática 8,5 9,5
Língua
portuguesa 9,5 9
Língua
inglesa 8 8,5
Matemática 7 8
Conhecimentos
de
economia 7 5
Médias Média
=
8,0 Média
=
8,0
Assunto

6. Medidas
de
Dispersão:
Desvio
Padrão
(σ)
Desvio
Padrão
(σ)
–
O
desvio
padrão
também
mede
o
afastamento
dos
elementos
da
amostra,
mas
atende
a
algumas
limitações
da
variância.
Definimos
essa
medida
como
a
raiz
quadrada
da
variância
dos
elementos
das
amostras.
Exemplo:
Para
preencher
uma
vaga
de
gerente
de
produção,
o
departamento
de
recursos
humanos
de
uma
empresa
realizou
um
teste
com
vários
candidatos,
selecionando
os
dois
melhores:
Leonor
e
Felipe.
A
tabela
abaixo
mostra
os
desempenhos
dos
dois
candidatos
nas
provas
a
que
se
submeteram:
Candidato
Leonor Felipe
Conhecimento
de
informática 8,5 9,5
Língua
portuguesa 9,5 9
Língua
inglesa 8 8,5
Matemática 7 8
Conhecimentos
de
economia 7 5
Médias Média
=
8,0 Média
=
8,0
Assunto
Como
saber
o
melhor
se
a
medida
de
tendência
central
fornece
um
empate?

7. Medidas
de
Dispersão:
Desvio
Padrão
(σ)
Candidato
Assunto Podemos
Leonor Felipe
Conhecimento
de
informática 8,5 9,5
Língua
portuguesa 9,5 9
Língua
inglesa 8 8,5
Matemática 7 8
Conhecimentos
de
economia 7 5
Médias Média
=
8,0 Média
=
8,0
uHlizar
o
desvio
padrão
para
determinar
o
quanto
cada
nota
está
afastada
da
média
aritméHca,
basta
efetuar
a
diferença
entre
a
nota
e
a
média,
nessa
ordem;
essa
diferença
é
chamada
do
desvio
da
nota.
Esses
desvios
são:

8. Medidas
de
Dispersão:
Desvio
Padrão
(σ)
Candidato
Assunto Podemos
Leonor Felipe
Conhecimento
de
informática 8,5 9,5
Língua
portuguesa 9,5 9
Língua
inglesa 8 8,5
Matemática 7 8
Conhecimentos
de
economia 7 5
Médias Média
=
8,0 Média
=
8,0
uHlizar
a
variância
para
determinar
o
quanto
cada
nota
está
afastada
da
média
aritméHca,
basta
efetuar
a
diferença
entre
a
nota
e
a
média,
nessa
ordem;
essa
diferença
é
chamada
do
desvio
da
nota.
Esses
desvios
são:
• 8,5
–
8,0
=
0,5
(a
nota
8,5
está
0,5
acima
da
média)
• 9,5
–
8,0
=
1,5
(a
nota
9,5
está
1,5
acima
da
média)
8,0
–
8,0
=
0,0
(a
nota
8,0
coincide
com
a
média)
• 7,0
–
8,0
=
-­‐
1,0
(as
duas
úl&mas
notas,
7,0,
estão
1,0
abaixo
da
média)

9. Medidas
de
Dispersão:
Desvio
Padrão
(σ)
Candidato
Assunto Podemos
Leonor Felipe
Conhecimento
de
informática 8,5 9,5
Língua
portuguesa 9,5 9
Língua
inglesa 8 8,5
Matemática 7 8
Conhecimentos
de
economia 7 5
Médias Média
=
8,0 Média
=
8,0
uHlizar
a
variância
para
determinar
o
quanto
cada
nota
está
afastada
da
média
aritméHca,
basta
efetuar
a
diferença
entre
a
nota
e
a
média,
nessa
ordem;
essa
diferença
é
chamada
do
desvio
da
nota.
Esses
desvios
são:
• 8,5
–
8,0
=
0,5
(a
nota
8,5
está
0,5
acima
da
média)
• 9,5
–
8,0
=
1,5
(a
nota
9,5
está
1,5
acima
da
média)
8,0
–
8,0
=
0,0
(a
nota
8,0
coincide
com
a
média)
• 7,0
–
8,0
=
-­‐
1,0
(as
duas
úl&mas
notas,
7,0,
estão
1,0
abaixo
da
média)
Calculando
as
variâncias
dos
conjuntos
de
notas
dos
candidatos,
temos:

10. Medidas
de
Dispersão:
Desvio
Padrão
(σ)
Candidato
Assunto Podemos
Leonor Felipe
Conhecimento
de
informática 8,5 9,5
Língua
portuguesa 9,5 9
Língua
inglesa 8 8,5
Matemática 7 8
Conhecimentos
de
economia 7 5
Médias Média
=
8,0 Média
=
8,0
uHlizar
a
variância
para
determinar
o
quanto
cada
nota
está
afastada
da
média
aritméHca,
basta
efetuar
a
diferença
entre
a
nota
e
a
média,
nessa
ordem;
essa
diferença
é
chamada
do
desvio
da
nota.
Esses
desvios
são:
• 8,5
–
8,0
=
0,5
(a
nota
8,5
está
0,5
acima
da
média)
• 9,5
–
8,0
=
1,5
(a
nota
9,5
está
1,5
acima
da
média)
8,0
–
8,0
=
0,0
(a
nota
8,0
coincide
com
a
média)
• 7,0
–
8,0
=
-­‐
1,0
(as
duas
úl&mas
notas,
7,0,
estão
1,0
abaixo
da
média)
Calculando
as
variâncias
dos
conjuntos
de
notas
dos
candidatos,
temos:

11. Medidas
de
Dispersão:
Desvio
Padrão
(σ)
Candidato
Assunto Podemos
Leonor Felipe
Conhecimento
de
informática 8,5 9,5
Língua
portuguesa 9,5 9
Língua
inglesa 8 8,5
Matemática 7 8
Conhecimentos
de
economia 7 5
Médias Média
=
8,0 Média
=
8,0
uHlizar
a
variância
para
determinar
o
quanto
cada
nota
está
afastada
da
média
aritméHca,
basta
efetuar
a
diferença
entre
a
nota
e
a
média,
nessa
ordem;
essa
diferença
é
chamada
do
desvio
da
nota.
Esses
desvios
são:
• 8,5
–
8,0
=
0,5
(a
nota
8,5
está
0,5
acima
da
média)
• 9,5
–
8,0
=
1,5
(a
nota
9,5
está
1,5
acima
da
média)
8,0
–
8,0
=
0,0
(a
nota
8,0
coincide
com
a
média)
• 7,0
–
8,0
=
-­‐
1,0
(as
duas
úl&mas
notas,
7,0,
estão
1,0
abaixo
da
média)
Calculando
as
variâncias
dos
conjuntos
de
notas
dos
candidatos,
temos:
Calculando
o
desvio
padrão
do
conjunto
de
notas,
σ(L)
,
σ(F)
,
temos:

12. Medidas
de
Dispersão:
Desvio
Padrão
(σ)
Candidato
Assunto Podemos
Leonor Felipe
Conhecimento
de
informática 8,5 9,5
Língua
portuguesa 9,5 9
Língua
inglesa 8 8,5
Matemática 7 8
Conhecimentos
de
economia 7 5
Médias Média
=
8,0 Média
=
8,0
uHlizar
a
variância
para
determinar
o
quanto
cada
nota
está
afastada
da
média
aritméHca,
basta
efetuar
a
diferença
entre
a
nota
e
a
média,
nessa
ordem;
essa
diferença
é
chamada
do
desvio
da
nota.
Esses
desvios
são:
• 8,5
–
8,0
=
0,5
(a
nota
8,5
está
0,5
acima
da
média)
• 9,5
–
8,0
=
1,5
(a
nota
9,5
está
1,5
acima
da
média)
8,0
–
8,0
=
0,0
(a
nota
8,0
coincide
com
a
média)
• 7,0
–
8,0
=
-­‐
1,0
(as
duas
úl&mas
notas,
7,0,
estão
1,0
abaixo
da
média)
Calculando
as
variâncias
dos
conjuntos
de
notas
dos
candidatos,
temos:
Calculando
o
desvio
padrão
do
conjunto
de
notas,
σ(L)
,
σ(F)
,
temos:

13. Medidas
de
Dispersão:
Desvio
Padrão
(σ)
Candidato
Assunto Podemos
Leonor Felipe
Conhecimento
de
informática 8,5 9,5
Língua
portuguesa 9,5 9
Língua
inglesa 8 8,5
Matemática 7 8
Conhecimentos
de
economia 7 5
Médias Média
=
8,0 Média
=
8,0
uHlizar
a
variância
para
determinar
o
quanto
cada
nota
está
afastada
da
média
aritméHca,
basta
efetuar
a
diferença
entre
a
nota
e
a
média,
nessa
ordem;
essa
diferença
é
chamada
do
desvio
da
nota.
Esses
desvios
são:
• 8,5
–
8,0
=
0,5
(a
nota
8,5
está
0,5
acima
da
média)
• 9,5
–
8,0
=
1,5
(a
nota
9,5
está
1,5
acima
da
média)
8,0
–
8,0
=
0,0
(a
nota
8,0
coincide
com
a
média)
• 7,0
–
8,0
=
-­‐
1,0
(as
duas
úl&mas
notas,
7,0,
estão
1,0
abaixo
da
média)
Calculando
as
variâncias
dos
conjuntos
de
notas
dos
candidatos,
temos:
Calculando
o
desvio
padrão
do
conjunto
de
notas,
σ(L)
,
σ(F)
,
temos:
Como
σ(L)
<
σ(F)
,
concluímos
que
Leonor
teve
um
desempenho,
nas
provas,
mais
regular
do
que
Felipe.

14. Medidas
de
Dispersão:
Desvio
Padrão
(σ)
Desvio
Padrão
(σ)
–
O
desvio
padrão
também
mede
o
afastamento
dos
elementos
da
amostra,
mas
atende
a
algumas
limitações
da
variância.
Definimos
essa
medida
como
a
raiz
quadrada
da
variância
dos
elementos
das
amostras.
Sendo
x
a
média
aritméHca
de
uma
amostra
de
números
x1,
x2,
x3,
...,
xn,
chama-­‐se
desvio
padrão,
que
se
indica
por
(σ),
o
número:
휎 = #(푥1 − 푥̅)2 + (푥2 − 푥̅)2 + (푥3 − 푥̅)2 +⋯+ (푥푛 − 푥̅)2
푛
ou
Σ (푥푖 − 푥̅)2 푛푖
=1
휎 = #
푛

15. FIM
da
Apresentação!