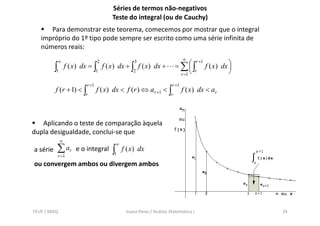
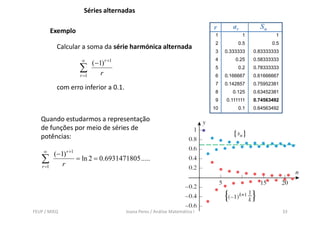
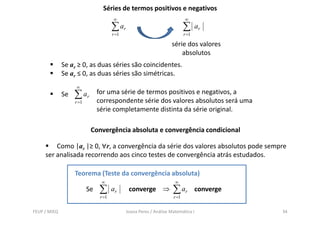
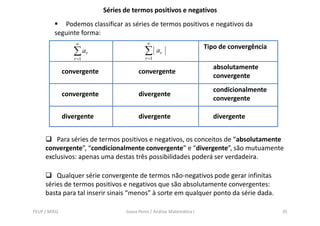
Este documento fornece uma introdução às séries de números reais, incluindo definições de séries convergentes e divergentes. Também discute propriedades importantes de séries, como séries telescópicas e geométricas, e apresenta vários testes para determinar a convergência de séries de termos não-negativos.