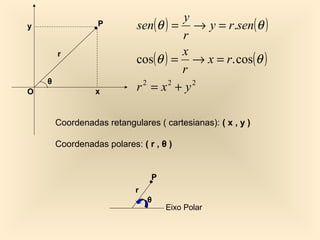
Este documento descreve o sistema de coordenadas polares, que representa a localização de um ponto no plano através da distância ao origem e do ângulo formado com o eixo x. Explica como converter entre coordenadas polares (r, θ) e cartesianas (x, y), e fornece exercícios de conversão entre os sistemas.

1. Coordenadas Polares
Calculo III

2. Dado um ponto P do plano, utilizando coordenadas
cartesianas (retangulares), descrevemos sua localização no plano
escrevendo P=(x,y) onde x é a projeção de P no eixo Ox e y, a
projeção no eixo Oy. Podemos também descrever a localização de
P a partir da distância de P à origem O do sistema e do ângulo
formado pelo eixo x e o segmento OP. Denotamos P=(r,θ) onde r
é a distância de P a O e o ângulo tomado no sentido anti–horário,
da parte positiva do eixo Ox ao segmento OP. Esta maneira
representar o plano é chamada Sistema de Coordenadas
Polares.

3. y
y P sen(θ ) = → y = r.sen(θ )
r
x
cos(θ ) = → x = r. cos(θ )
r
r
θ
O x r =x +y
2 2 2
Coordenadas retangulares ( cartesianas): ( x , y )
Coordenadas polares: ( r , θ )
P
r
θ
Eixo Polar

4. Exercícios:
1) Encontre as coordenadas retangulares do ponto P cujas coordenadas
polares são ( 6, 2π/3).
 2π 
Substituindo as coordenadas ( r,θ ) =  6 ,  temos :
 3 
 2π 
x = r.cos(θ ) = 6.cos  = −3
 3 
 2π 
y = r.sen (θ ) = 6.sen =3 3
 3 
(
Portanto, as coordenadas retangulares de P são − 3,3 3 )

5. Exercícios:
2) Encontre as coordenadas polares do ponto P cujas coordenadas
(
retangulares são − 2,2 3 : )
y
y 2 3
2 3
tg ( α ) = = = 3 → α = 60°
x 2
θ 2π
Assim θ = 180° - 60° = 120° =
−2 x 3

6. r =x +y ⇒r=
2 2 2
( − 2) 2
(
+ 2 3 ) 2
→r =4
 2π 
As coordenadas polares do ponto P são  4, :
 3 

7. 3) Encontre as coordenadas polares do ponto P cujas coordenadas
retangulares são ( )
3 ,− 3 :
y 3
tg ( α ) = = = 1 → α = 45°
x 3
7π
Assim θ = 360° - 45° = 315° =
4
r = x2 + y2 = 3 + 3 = 6
 7π 
As coordenadas polares são  6 , 
 4 

8. Escreva a equação da circunferência ( x - 1) + ( y − 1) = 2
2 2
em coordenadas polares
(x – 1)² + (y – 1)² = 2 → x² - 2x + y² - 2y = 0
Subst:
(r cos θ)² - 2 (r cos θ) + (r sen θ)² – 2(r sen θ)
r² cos θ² - 2 r cos θ + r² sen θ² - 2 r senθ = 0
r² (cosθ² + senθ² ) – 2 r cosθ - 2 r senθ = 0
r² - 2 r cosθ - 2 r senθ = 0 div. r
r – 2 cosθ - 2 senθ = 0

9. Escreva as equações polares dadas para coordenadas retangulares :
a)r = 2 cos(θ )
multiplicando por r temos → r 2 = 2.r cos(θ )
se r = x + y e x = r cos(θ ) temos
2 2 2
r 2 = 2.r cos(θ ) pode ser escrito como x 2 + y 2 = 2 x

10. b)r = 3 cos(θ ) + 3sen(θ )
multiplicando por r temos → r 2 = 3r cos(θ ) + 3rsen(θ )
se r 2 = x 2 + y 2 e x = r cos(θ ) e y = r sen (θ ) temos
r 2 = 3r cos(θ ) + 3rsen(θ ) pode ser escrito como x 2 + y 2 = 3 x + 3 y
x 2 + 3x + y 2 + 3 y