1. O documento apresenta 5 exercícios resolvidos sobre dinâmica de rotação, incluindo barras girando livremente, centrífugas e momentos de inércia.
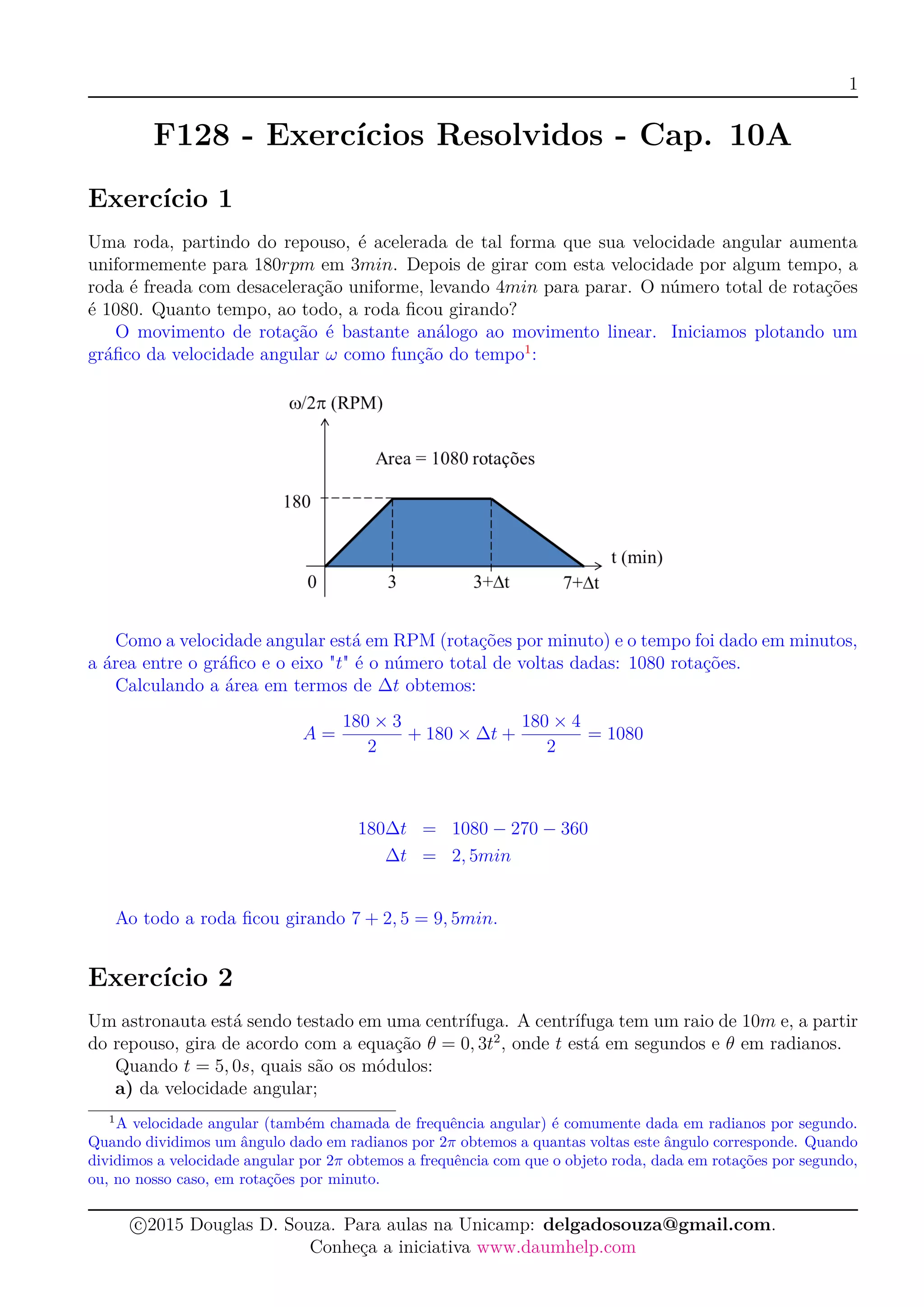
2. No primeiro exercício, uma roda é acelerada e desacelerada uniformemente e o tempo total que girou é calculado.
3. No segundo, velocidades angulares, lineares e acelerações de um astronauta em uma centrífuga são determinadas.
4. Nos demais, momentos de inércia de sistemas compost