Séries fourier cap_1 Funções Periódicas
•
2 gostaram•2,513 visualizações
Séries fourier cap_1 Funções Periódicas
Denunciar
Compartilhar
Denunciar
Compartilhar
Baixar para ler offline
Recomendados
Mais conteúdo relacionado
Mais procurados
Mais procurados (20)
Passar um factor para dentro e para fora do radical

Passar um factor para dentro e para fora do radical
Gráficos de funções afim - Matemática 8º ano - Resumo da matéria

Gráficos de funções afim - Matemática 8º ano - Resumo da matéria
Séries fourier cap_3 Exemplos de Séries de Fourier

Séries fourier cap_3 Exemplos de Séries de Fourier
Cap4 - Parte 6 - Distribuições Discretas Exercicios Resolvidos

Cap4 - Parte 6 - Distribuições Discretas Exercicios Resolvidos
Destaque
Destaque (20)
Séries fourier cap_2 Relações Trigonométricas Elementares

Séries fourier cap_2 Relações Trigonométricas Elementares
CONVERSOR ANALÓGICO/DIGITAL COM SAMPLE AND HOLDCONVERSOR ANALÓGICO/DIGITAL CO...

CONVERSOR ANALÓGICO/DIGITAL COM SAMPLE AND HOLDCONVERSOR ANALÓGICO/DIGITAL CO...
Quem foi ptolomeu e quais suas contribuições à trigonometria 

Quem foi ptolomeu e quais suas contribuições à trigonometria
www.AulasDeMatematicaApoio.com - Matemática - Ciclo Trigonométrico

www.AulasDeMatematicaApoio.com - Matemática - Ciclo Trigonométrico
Semelhante a Séries fourier cap_1 Funções Periódicas
Semelhante a Séries fourier cap_1 Funções Periódicas (20)
Séries fourier cap_5 Desenvolvimento em Meio Período

Séries fourier cap_5 Desenvolvimento em Meio Período
Aplicação da Transformada de Laplace na Determinação de Tensões e Correntes e...

Aplicação da Transformada de Laplace na Determinação de Tensões e Correntes e...
Trabalho de matematica_as_funções_trigonométricas_verdadeira[1]![Trabalho de matematica_as_funções_trigonométricas_verdadeira[1]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Trabalho de matematica_as_funções_trigonométricas_verdadeira[1]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Trabalho de matematica_as_funções_trigonométricas_verdadeira[1]
13.2 derivadas e integrais de funções vetoriais (1)

13.2 derivadas e integrais de funções vetoriais (1)
Mais de Ciro Marcus
Mais de Ciro Marcus (17)
FONTE DE TENSÃO USANDO REGULADOR EM CIRCUITO INTEGRADO

FONTE DE TENSÃO USANDO REGULADOR EM CIRCUITO INTEGRADO
Projeto de Controle de Posição entre veículos, Análise de Sistemas III

Projeto de Controle de Posição entre veículos, Análise de Sistemas III
Análise de Sistemas II - Modelamento e identificação de sistemas

Análise de Sistemas II - Modelamento e identificação de sistemas
AM-DSB - Amplitude Modulation with Double Side-Band Modulção em Amplitude

AM-DSB - Amplitude Modulation with Double Side-Band Modulção em Amplitude
AM-DSB - Amplitude Modulation with Double Side-Band (modulação em amplitude)

AM-DSB - Amplitude Modulation with Double Side-Band (modulação em amplitude)
PROJETO DE FILTROS DIGITAIS E SIMULAÇÕES NO MATLAB 

PROJETO DE FILTROS DIGITAIS E SIMULAÇÕES NO MATLAB
Trabalho de Ergonomia voltado a Engenharia - Posto de trabalho

Trabalho de Ergonomia voltado a Engenharia - Posto de trabalho
Engenharia Eletronica e de Telecomunicação Fluxograma4404

Engenharia Eletronica e de Telecomunicação Fluxograma4404
Último
Aula de tema de redação desenvolvida pela professora Ana Augusta Lages, graduanda em Letras pela UFMGTema de redação - As dificuldades para barrar o casamento infantil no Brasil ...

Tema de redação - As dificuldades para barrar o casamento infantil no Brasil ...AnaAugustaLagesZuqui
Último (20)
Acessibilidade, inclusão e valorização da diversidade

Acessibilidade, inclusão e valorização da diversidade
ATIVIDADE 2 - DESENVOLVIMENTO E APRENDIZAGEM MOTORA - 52_2024

ATIVIDADE 2 - DESENVOLVIMENTO E APRENDIZAGEM MOTORA - 52_2024
Tema de redação - As dificuldades para barrar o casamento infantil no Brasil ...

Tema de redação - As dificuldades para barrar o casamento infantil no Brasil ...
Slides Lição 06, Central Gospel, O Anticristo, 1Tr24.pptx

Slides Lição 06, Central Gospel, O Anticristo, 1Tr24.pptx
E a chuva ... (Livro pedagógico para ser usado na educação infantil e trabal...

E a chuva ... (Livro pedagógico para ser usado na educação infantil e trabal...
ATIVIDADE 2 - DESENVOLVIMENTO E APRENDIZAGEM MOTORA - 52_2024

ATIVIDADE 2 - DESENVOLVIMENTO E APRENDIZAGEM MOTORA - 52_2024
Aprender as diferentes formas de classificar as habilidades motoras é de extr...

Aprender as diferentes formas de classificar as habilidades motoras é de extr...
O estudo do controle motor nada mais é do que o estudo da natureza do movimen...

O estudo do controle motor nada mais é do que o estudo da natureza do movimen...
Polígonos, Diagonais de um Polígono, SOMA DOS ANGULOS INTERNOS DE UM POLÍGON...

Polígonos, Diagonais de um Polígono, SOMA DOS ANGULOS INTERNOS DE UM POLÍGON...
Novena de Pentecostes com textos de São João Eudes

Novena de Pentecostes com textos de São João Eudes
atividade-de-portugues-paronimos-e-homonimos-4º-e-5º-ano-respostas.pdf

atividade-de-portugues-paronimos-e-homonimos-4º-e-5º-ano-respostas.pdf
GUIA DE APRENDIZAGEM 2024 9º A - História 1 BI.doc

GUIA DE APRENDIZAGEM 2024 9º A - História 1 BI.doc
O estudo do controle motor nada mais é do que o estudo da natureza do movimen...

O estudo do controle motor nada mais é do que o estudo da natureza do movimen...
República Velha (República da Espada e Oligárquica)-Sala de Aula.pdf

República Velha (República da Espada e Oligárquica)-Sala de Aula.pdf
Séries fourier cap_1 Funções Periódicas
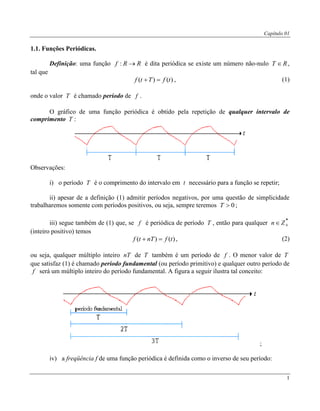
- 1. Capítulo 01 1 1.1. Funções Periódicas. Definição: uma função RRf : é dita periódica se existe um número não-nulo RT , tal que )()( tfTtf , (1) onde o valor T é chamado período de f . O gráfico de uma função periódica é obtido pela repetição de qualquer intervalo de comprimento T : Observações: i) o período T é o comprimento do intervalo em t necessário para a função se repetir; ii) apesar de a definição (1) admitir períodos negativos, por uma questão de simplicidade trabalharemos somente com períodos positivos, ou seja, sempre teremos 0T ; iii) segue também de (1) que, se f é periódica de período T , então para qualquer * Zn (inteiro positivo) temos )()( tfnTtf , (2) ou seja, qualquer múltiplo inteiro nT de T também é um periodo de f . O menor valor de T que satisfaz (1) é chamado período fundamental (ou período primitivo) e qualquer outro período de f será um múltiplo inteiro do período fundamental. A figura a seguir ilustra tal conceito: ; iv) a freqüência f de uma função periódica é definida como o inverso de seu período:
- 2. Fabiano J. Santos 2 T 1 , e nos dá o número de repetições (ciclos) em cada intervalo unitário em t . Se t é medido em segundos então a freqüência é o número de ciclos por segundo (Hertz). Um outro tipo de freqüência utilizada é a freqüência angular, dada por 2; v) o inverso do período fundamental é chamado freqüência fundamental. Exemplo 01: a função )sen(ty é periódica com período fundamental 2T e período n2 (n inteiro positivo), conforme ilustra o gráfico Exemplo 02: a função )cos(ty é periódica com período fundamental 2T e período n2 (n inteiro positivo), conforme ilustra o gráfico
- 3. Capítulo 01 3 Exemplo 03: a função constante ctfy )( tem como período qualquer valor 0T , e não possui período fundamental. As duas proposições a seguir nos dão duas propriedades importantes das funções periódicas, as quais utilizaremos freqüentemente. Proposição 01: seja f uma função periódica de período T , então: i) )(atf , 0a , é periódica de período a T ; ii) )( b t f , 0b , é periódica de período bT . Provas: i) ).()]([)( ** aTatfTtafatf Fazendo atu , obtemos )()( * aTufuf . Logo pela hipótese concluímos que TaT * donde a T T * . ii) )()]( 1 [)( * * b T b t fTt b f b t f . Fazendo b t u , obtemos )()( * b T ufuf . Logo pela hipótese concluímos que T b T * donde bTT * . Proposição 02: sejam f e g duas funções periódicas com o mesmo período T e a e b duas constantes reais quaisquer. A função h definida por )()()( tbgtafth , (3) também é periódica de período T . Prova: aqui a prova é muito simples e pode ser obtida diretamente de (3), a saber )()()()()()( thtbgtafTtbgTtafTth .
- 4. Fabiano J. Santos 4 Exemplo 04: de acordo com a proposição (01) temos os seguintes exemplos: a) )2sen( t , )2cos( t período b) )2sen( t , )2cos( t período 1 c) ) 2 sen( T t , ) 2 cos( T t período T Além disto, para todo * Zn (inteiro positivo) temos que as funções ) 2 sen( T tn e ) 2 cos( T tn (4) possuem ambas período T , haja vista qualquer múltiplo inteiro do período fundamental também ser período. E pela proposição (2), a função ) 2 cos() 2 sen()( T tn b T tn axh , (5) também possui período T . Proposição 03: sejam nffff ,...,,, 321 funções periódicas de período T . Então a função )(...)()()()( 321 tftftftfth n , (6) dada pela combinação linear de nffff ,...,,, 321 também é periódica de período T . A prova é análoga à da proposição (02) e pode ser obtida pelo princípio da indução. 1.2. Séries Trigonométricas. Extrapolando a proposição (03), sejam ,...,...,,, 321 nffff funções periódicas de mesmo período T , a série infinita dada por ...)(...)()()( 321 tftftftf n , (7) define, nos pontos onde converge, uma função periódica de mesmo período T . Assim podemos definir a função ...)(...)()()()( 321 tftftftfth n , (8) tal que
- 5. Capítulo 01 5 )()( Tthth . (9) Esta última afirmação será de crucial importância para nosso trabalho posterior, uma vez que trabalharemos com séries infinitas da forma 1 ) 2 cos() 2 sen( n T tn T tn ...) 2 cos() 2 sen(...) 2 cos() 2 sen( T tn T tn T t T t (10) denominada série trigonométrica. Observe que cada termo da série em (10) possui período T , desta forma, nos pontos onde a série converge ela define uma função periódica de período T . Para conveniência nos cálculos, a partir de agora consideraremos LT 2 , onde L é chamado meio-período. Com esta convenção a equação (10) torna-se 1 )cos()sen( n L tn L tn ...)cos()sen(...)cos()sen( L tn L tn L t L t (11) que será nossa forma trabalhável nos próximos capítulos. Problemas: 1. Determine se cada uma das funções a seguir é ou não períódica. Caso seja determine também seu período fundamental T e o meio-período L . a) )sen( T t b) )cos( t c) )2senh( t d) )tan( t e) 2 t f) )5sen( t g) )cos(mt h) t e i) )5sen()4sen()3cos( ttt j) ) 13 4 cos() 11 sen() 7 2 sen() 3 cos( tttt k) ,...3,2,1,0, 122,1 212,0 )( n ntn ntn tf (sugestão: esboce o gráfico para alguns valores de n) l) ,...3,2,1,0, 122,1 212,)1( )( n ntn ntn tf n 02*. Seja RRg : uma função periódica de período T e integrável em toda a reta R . Mostre que
- 6. Fabiano J. Santos 6 Tb b Ta a dttgdttg )()( (ou seja, não importa em qual intervalo se dá a integração o valor será sempre o mesmo desde que o tamanho deste intervalo seja o próprio período da função. Geometricamente isto é óbvio. Por quê?)
