Atividades graphmatica( introd. trigonometria funções)
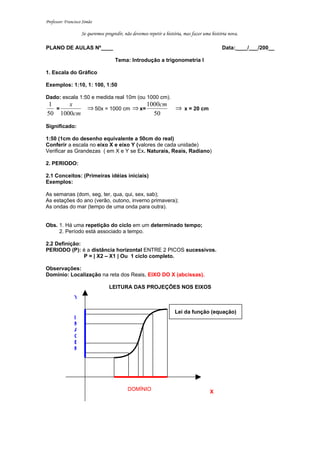
- 1. Professor: Francisco Simão Se queremos progredir, não devemos repetir a história, mas fazer uma história nova. PLANO DE AULAS Nº____ Data:____/___/200__ Tema: Introdução a trigonometria I 1. Escala do Gráfico Exemplos: 1:10, 1: 100, 1:50 Dado: escala 1:50 e medida real 10m (ou 1000 cm). 1 x 1000cm = ⇒ 50x = 1000 cm ⇒ x= ⇒ x = 20 cm 50 1000cm 50 Significado: 1:50 (1cm do desenho equivalente a 50cm do real) Conferir a escala no eixo X e eixo Y (valores de cada unidade) Verificar as Grandezas ( em X e Y se Ex. Naturais, Reais, Radiano) 2. PERIODO: 2.1 Conceitos: (Primeiras idéias iniciais) Exemplos: As semanas (dom, seg, ter, qua, qui, sex, sab); As estações do ano (verão, outono, inverno primavera); As ondas do mar (tempo de uma onda para outra). Obs. 1. Há uma repetição do ciclo em um determinado tempo; 2. Período está associado a tempo. 2.2 Definição: PERIODO (P): é a distância horizontal ENTRE 2 PICOS sucessivos. P = | X2 – X1 | Ou 1 ciclo completo. Observações: Domínio: Localização na reta dos Reais, EIXO DO X (abcissas). LEITURA DAS PROJEÇÕES NOS EIXOS Y Lei da função (equação) I M A G E M DOMÍNIO X
- 2. Professor: Francisco Simão Se queremos progredir, não devemos repetir a história, mas fazer uma história nova. 3. AMPLITUDE: Amplitude: 3.1 Conceitos: (Primeiras idéias iniciais) Exemplos: Altura de uma montanha; Altura de um edifício; Altura da profundidade do leito de um rio ou lagoa; Altura do Fundo de um poço. 3.2 Definição: AMPLITUDE (A): é a METADE da distância VERTICAL ENTRE DOIS PICOS (máximo e mínimo). ou A = | y2máx – y1mín | / 2. ( valor escalar ). Observações: ATENÇÃO: 1. Traçar eixo de SIMETRIA ENTRE 2 PICOS quando o GRÁFICO É DESLOCADO; 2. Máximo: concavidade para baixo; 3. Mínimo: concavidade para cima; 4. Valores entre picos em módulo ( ou seja sempre positivo). 4. IMAGEM 4.1 Conceitos: (Primeiras idéias iniciais) Exemplos: Imagem refletida de um objeto no espelho; Comprimento da sombra da vara causada pela luz solar; Solstício de verão (instante em que a sombra é mínima-meio dia-define o início de Verão); Solstício de inverno (é o instante em que a sombra é máxima-define o início de inverno). Sombra de um objeto quando a luz incide sobre o objeto. 4.2 Definição: IMAGEM: O conjunto formado pelos segundos elementos dos pares ordenados (x,y) pertencente f. Observações: IMAGEM (Im): Localização EIXO DO Y (ordenadas) Y Lei da função (equação) I M A G E M X DOMÍNIO
- 3. Professor: Francisco Simão Se queremos progredir, não devemos repetir a história, mas fazer uma história nova. 4.3 IMAGEM: Exemplos: Formas de representar a IMAGEM (Im): Y • na reta real; 3 4 5 6 R • na forma de solução: S={y ∈ R / 3 ≤ y ≤ 6} • forma de intervalos: D( f ) = R , ∀ y ∈ R [ 3, 6 ] outra forma D=R, [ 3, 6 ] y ∈ R 5. DOMÍNIO: 5.1 Definição: é todos os valores de x (x ∈ R) que tornam possíveis as operações indicada na lei de formação. Outra definição. Definição: o conjunto formado pelos primeiros elementos dos pares ordenados (x,y) pertencentes a f . Domínio: Formas de representar O DOMÍNIO: • na reta real; X 3 4 5 6 R • na forma de solução: S = { x ∈ R / 3 ≤ x ≤ 6} • forma de intervalos: D( f ) = R, ∀ x ∈ R [ 3, 6 ] outra forma D = R, [ 3, 6] x ∈ R 6. Análise do gráfico Procedimento: • 1º conferir a escala (grandezas e unidades) • 2º projetar a imagem da função no eixo Y • 3º traçar eixo de Simetria Ortogonal a (IMAGEM) • 4º localizar o valor da amplitude • 5º localizar Período e domínio Ou Verificar escala (grandezas e unidades) Calcular valor escalar entre picos Maximo e Mínimo A = | y2max – y1min | / 2 1. Dado a função: y = 2+3 cos( x) y = 2+ 3 cos (x) {x: - pi, 3pi}
- 4. Professor: Francisco Simão Se queremos progredir, não devemos repetir a história, mas fazer uma história nova. X1 Período X2 Y2max Imagem (Im) Amplitude (A) Y1max Domínio com Intervalo Exemplo anterior: a) Amplitude: A = 3 b) Período: P= 2π c) O domínio do gráfico: D = R , ∀ x ∈ R [ -π, 3π] = { x ∈ R | -π ≤ x ≤ 3π } d) A imagem : Im = [ -1, 5]= ∀ y ∈ R [ -1,5 ] ou Im= { y ∈ R | − 1 ≤ y ≤ 5}
- 5. Professor: Francisco Simão Se queremos progredir, não devemos repetir a história, mas fazer uma história nova. a) y = 2 sin(x) : lei da função b) y= 2 sin(x) { x: - pi, pi } : intervalo da função c) x= 2 sin(x) { y: - 2, 2} : projeção da imagem com intervalo d) y=0 2 sin(x) { x: - pi, pi } : projeção do domínio com intervalo e) amplitude: A = | - 2 – (2) ] / 2 = │ - 4 │/ 2 = 4/2 = 2 logo: A = 2 REFAÇA O GRÁFICO PARA: a) y = 3 sin(x) lei da Função b) y = 3 sin(x) { y: ___, ___ } intervalo da função c) x = 3 sin(x) { y: ___, ___ } projeção da imagem com intervalo d) y = ____ 3sin { x: ___, ___}: projeção do domínio com intervalo e) Amplitude:___________________ a) y =1+ 2 sin(x) lei da Função b) y = 1+2 sin(x) { y: ___, ___ } intervalo da função c) x = 1+2 sin(x) { y: ___, ___ } projeção da imagem com intervalo d) y = ___ 1+2 sin { x: ___, ___}: projeção do domínio com intervalo e) Amplitude: ________________
- 6. Professor: Francisco Simão Se queremos progredir, não devemos repetir a história, mas fazer uma história nova. Ficha Nº _____ Data: ___/ ____/ 200___ Introdução a Trigonometria I 1. Dê as definições (significado): a) DOMÍNIO: ______________________________________________________________________ ______________________________________________________________________ ___________________________________________________________________ b) IMAGEM: ______________________________________________________________________ ______________________________________________________________________ ___________________________________________________________________ c) PERÍODO: ______________________________________________________________________ ____________________________________________________________________ d) AMPLITUDE: ______________________________________________________________________ ______________________________________________________________________ 2. atividades 2.1 Faça a representação da modelagem gráfica proposta: __________________________ 2.2 Determine os valores escalares e intervalos dos gráficos, Amplitude (A), Período (P), Imagem (Im) e Domínio(D). Período: P =__________________________________________________________________ Amplitude: A =________________________________________________________________ Imagem: Im =_________________________________________________________________ Domínio: D = _________________________________________________________________
- 7. Professor: Francisco Simão Se queremos progredir, não devemos repetir a história, mas fazer uma história nova. 2.3 Determine os valores escalares e intervalos dos gráficos, Amplitude (A), Período (P), Imagem (Im) e Domínio(D). Período: P =__________________________________________________________________ Amplitude: A =________________________________________________________________ Imagem: Im =_________________________________________________________________ Domínio: D = _________________________________________________________________ 2.4 Período: P =__________________________________________________________________ Amplitude: A =________________________________________________________________ Imagem: Im =_________________________________________________________________ Domínio: D = _________________________________________________________________
- 8. Professor: Francisco Simão Se queremos progredir, não devemos repetir a história, mas fazer uma história nova. 2.5 Idem para y = - 6 cos ( 1/2 x) y = - 6 cos ( 1/2 x) {x: -3pi, 4pi} a) Amplitude: A = __________________________ b) Período: P = __________________________ c) Imagem: Im = ____________________________________________________________ d) Domínio: D = ____________________________________________________________ 2.6 y = 2 + sen x + | sen x │ y = 2 + sin (x) + abs ( sin (x)) a) Amplitude: A = __________________________ b) Período: P = __________________________ c) Imagem: Im = ___________________________________________________________ d) Domínio: D = ___________________________________________________________
- 9. Professor: Francisco Simão Se queremos progredir, não devemos repetir a história, mas fazer uma história nova. 2.7 y = - │ ( 8 sen (2x)) │ y = - abs ( 8 sin (2x)) {x: - 1/2 pi, 3pi} a) Amplitude: A = __________________________ b) Período: P = __________________________ c) Imagem: Im = ____________________________________________________________ d) Domínio: D = ____________________________________________________________ 2.8 y = | 4 sen(x) │ y = abs ( 4 sin (x)) a) Amplitude: A = __________________________ b) Período: P = __________________________ c) Imagem: Im = ____________________________________________________________ d) Domínio: D = ____________________________________________________________
- 10. Professor: Francisco Simão Se queremos progredir, não devemos repetir a história, mas fazer uma história nova. 2.9 y = 1+ sen (x) y = 1+ sen (x) { x: -pi, 3pi} a) Amplitude: A = __________________________ b) Período: P = __________________________ c) Imagem: Im = ____________________________________________________________ d) Domínio: D = ____________________________________________________________ 2.10 y = sen (x) –2 cos (2x) y = sin (x) – 2 cos (2x) a) Amplitude: A = __________________________ b) Período: P = __________________________ c) Imagem: Im = ____________________________________________________________ d) Domínio: D = ____________________________________________________________
- 11. Professor: Francisco Simão Se queremos progredir, não devemos repetir a história, mas fazer uma história nova. 2.11 y = sen (x) +1 – cos (2x) + cos (x) a) Amplitude: A = __________________________ b) Período: P = __________________________ c) Imagem: Im = ____________________________________________________________ d) Domínio: D = ____________________________________________________________