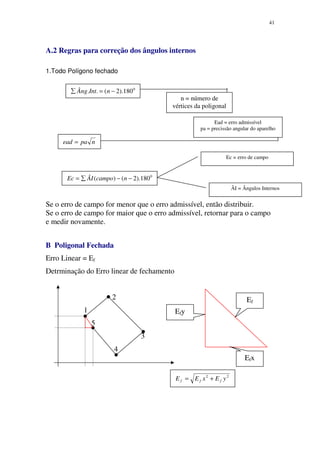
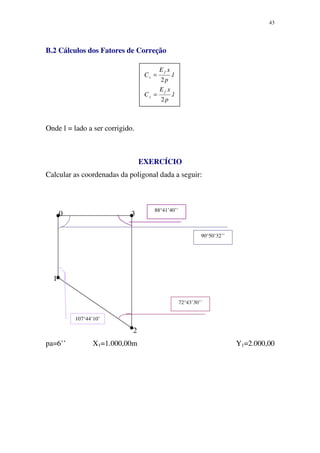
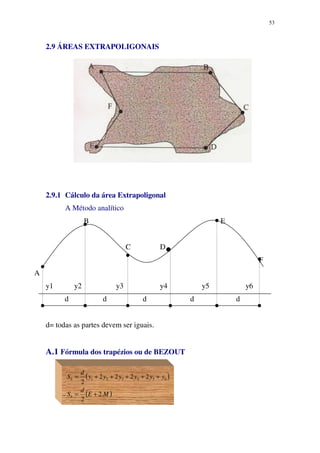
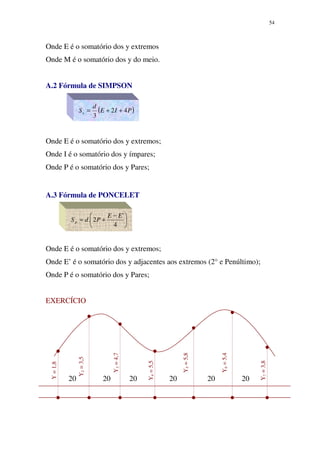
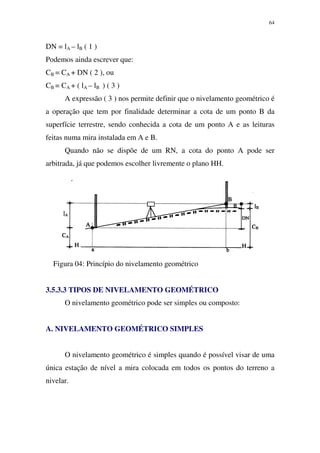
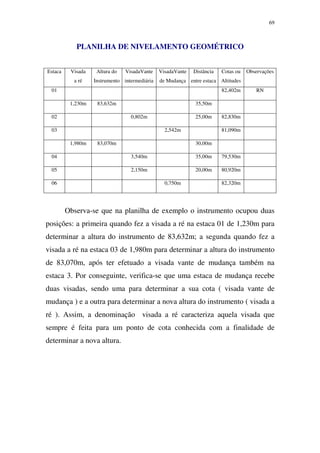
1. O documento discute os conceitos básicos e métodos de topografia para engenheiros e arquitetos. 2. Apresenta as definições de topografia, geodésia e seus objetivos, além dos tipos de levantamentos topográficos. 3. Detalha os processos e instrumentos utilizados em levantamentos topográficos, medições de distâncias, ângulos, nivelamento e representação gráfica do relevo.

1. TOPOGRAFIA BÁSICA PARA
ENGENHEIROS E ARQUITETOS
Antonio Henriques Bento
Rosane Maciel Vargas
Manaus
Agosto/1999

2. SUMÁRIO
1 HISTÓRICO ........................................................................................... 1
2 TOPOGRAFIA ....................................................................................... 3
2.1 Levantamento topográfico ................................................................. 4
A. Expedito ....................................................................................... 4
B. Comum ......................................................................................... 5
C. Precisão ........................................................................................ 5
2.2 Divisões da Topografia ..................................................................... 6
A. Topometria ................................................................................... 6
A1. Planimetria ........................................................................... 6
A2. Altimetria ............................................................................. 6
B. Topologia ..................................................................................... 6
2.3 Partes de um trabalho de Topografia ................................................ 6
2.3.1 Parte Matemática ..................................................................... 6
2.3.2 Parte Interpretativa .................................................................. 6
2.3.3 Parte Artística .......................................................................... 6
2.4 Unidades de Medida ......................................................................... 8
2.4.1 Medida de distância ................................................................. 8
2.4.2 Medida de superfície ................................................................ 9
2.4.3 Medida de volume .................................................................. 10
2.4.4 Medida de massa .................................................................... 10
2.4.5 Medida de ângulo ................................................................... 11
A. Sistema Centesimal de divisão de áreas .......................... 11
B. Sistema sexagesimal de divisão de arcos ......................... 11
C. Radiano ............................................................................ 11
D. Milésimo .......................................................................... 12
2.5 Medição de ângulos ......................................................................... 13

3. 2.5.1 Ângulos Azimutais ................................................................. 14
A. Rumos .............................................................................. 15
B. Azimutes .......................................................................... 16
B1. Contrazimute ou azimute à ré ................................... 17
B2. Relações existentes entre azimute e contrazimute .... 17
2.5.2 Ângulos goniométricos .......................................................... 20
A. Ângulo de flexão .............................................................. 21
B. Ângulo de deflexão .......................................................... 21
C. Sentido dos ângulos goniométricos ................................. 22
2.5.3 Ângulos azimutais x ângulos goniométricos ......................... 22
2.5.4 Cálculo de rumos e azimutes a partir de ângulos goniométricos
................................................................................................ 23
2.5.4.1 Fórmula geral dos azimutes ...................................... 26
A. Fórmula geral para ângulos de flexão .................. 26
B. Fórmula geral para ângulos de deflexão .............. 28
2.5.5 Limites do azimute ................................................................. 28
2.6 Medidas de distância ....................................................................... 31
2.6.1 Processos de medida direta .................................................... 31
A. Processos de baixa precisão ............................................... 31
B. Processos de média precisão .............................................. 32
C. Processos de alta precisão .................................................. 32
2.6.2 Técnica de Medida com Trena ............................................... 33
2.6.3 Técnica de Medidas Indiretas ................................................. 34
2.7 Métodos de Levantamento Topográfico ......................................... 35
2.7.1 Método do Caminhamento Perimétrico ou Método da
Poligonal.............................................................................. 35
2.7.2 Método da Irradiação ............................................................. 37
2.7.3 Cálculo da Poligonal .............................................................. 38

4. A. Poligonal Aberta .............................................................. 38
A.1 Cálculo das Coordenadas dos Pontos ...................... 39
A.2 Regras para a Correção de Ângulos Internos .......... 41
B. Poligonal Fechada ............................................................ 41
B.1 Cálculo do Erro Linear Relativo ( Er ) ..................... 42
B.2 Cálculo dos Fatores de Correção .............................. 43
B.3 Cálculo da Área de Poligonais Fechadas através das
Coordenadas de seus vértices .................................. 45
B.3.1 Fórmula de Gauss ............................................ 45
2.7.4 Método da Interseção ............................................................. 46
2.7.5 Método das Coordenadas Retangulares ................................. 50
A. Aplicação .......................................................................... 50
B. Precisão ............................................................................ 51
2.8 Levantamento dos Detalhes ............................................................ 51
2.8.1 Definição dos Detalhes ........................................................... 51
2.8.2 Método de Levantamento de Detalhes ................................... 52
2.9 Áreas Extra Poligonais .................................................................... 53
2.9.1 Cálculo da Área Extra Poligonal ............................................ 53
A. Método Analítico .............................................................. 53
A.1 Fórmula dos Trapézios ou de Bezout ....................... 53
A.2 Fórmula de Simpson ................................................ 54
A.3 Fórmula de Poncelet ................................................. 54
3 ALTIMETRIA ..................................................................................... 57
3.1 Cotas e Altitudes ............................................................................. 57
3.2 Diferença de Nível .......................................................................... 57
3.3 Referência de Nível ......................................................................... 58
3.4 Nivelamento .................................................................................... 58
3.5 Tipos de Nivelamento ..................................................................... 59

5. 3.5.1 Nivelamento Barométrico ...................................................... 59
3.5.2 Nivelamento Trigonométrico ................................................. 60
3.5.3 Nivelamento Geométrico ....................................................... 62
3.5.3.1 Material Utilizado ..................................................... 62
A. Níveis ................................................................... 62
B. Miras .................................................................... 63
3.5.3.2 Princípio do Levantamento Geométrico ................... 63
3.5.3.3 Tipos de Nivelamento Geométrico ........................... 64
A. Nivelamento Geométrico Simples .................... 64
B. Nivelamento Geométrico Composto ................ 66
3.5.4 Erro de Nivelamento ............................................................. 68
3.5.5 Planilha de Nivelamento ....................................................... 68
3.5.6 Verificação do Cálculo da Planilha ....................................... 70
3.6 Curvas de nível ............................................................................. 73
3.6.1 Traçado das Curvas de Nível ............................................... 75
3.6.2 Interpolação ......................................................................... 77
3.6.3 Determinação dos Pontos de Cota Inteira ........................... 78
3.7 Elaboração de um Perfil Topográfico a partir da Planta Topográfica
com Curvas de Nível .................................................................... 83
3.8 Determinação da Cota de um Ponto situado entre Curvas de Nível
........................................................................................................ 84
3.9 Elaboração de um Perfil Topográfico a partir de pontos Nivelados
....................................................................................................... 86
3.10 Determinação da Declividade entre dois Pontos ........................ 87
4 NOÇÕES DE TERRAPLANAGEM ...................................................89
4.1 Cálculo de Volumes ........................................................................ 92
4.1.1 Método de Perfis Paralelos Equidistantes .............................. 92
4.1.2 Método das Curvas de Nível .................................................. 94

6. 4.2 Traçado da Linha de OFF-SET de um talude .................................. 96
5 NOÇÕES DE GEODÉSIA................................................................. 100
5.1 Transporte de Coordenadas ........................................................... 102
5.1.1 Classificação das Triangulações ........................................... 103
5.1.2 Triangulação Geodésica ....................................................... 105
5.1.3 Determinação do Excesso Esférico ...................................... 106
5.2 Trilateração .................................................................................... 108
5.3 Convergência Meridiana ............................................................... 109
6 EXEMPLO DE UM LEVANTAMENTO TOPOGRÁFICO.......... 113
7 MEMORIAL DESCRITIVO............................................................. 114
7.1 Modelo I de Memorial Descritivo ................................................. 114
7.2 Modelo II de Memorial Descritivo ................................................ 115
7.3 Modelo III de Memorial Descritivo .............................................. 116
BIBLIOGRAFIA CONSULTADA...................................................... 118

7. 1
1 HISTÓRICO
Os instrumentos e processos utilizados para cadastramento de
propriedades rurais nos foram passados pelos egípcios, gregos e árabes.
Plantas, cartas militares e geográficas, organizadas nos primórdios da
Topografia, são mencionadas por Laussedat em sua obra “História da
Topografia”( Espartel, 1978 ).
Segundo Espartel ( op.cit. ), o desenvolvimento da Matemática e da
Física nos últimos séculos, possibilitaram a passagem da topografia do
empirismo às bases de uma autêntica ciência. O primeiro trabalho
topográfico realizado com técnica e estilo próprio, foi a Carta da França
compilada pelo cartógrafo italiano Cassini e publicada no início do século
XIX pela Academia Francesa.
O progresso dos métodos desenvolvidos pela Topografia teve
contribuição eficiente do engenheiro suiço Henrique Wild, do geodesista
italiano Ignazio Porro, de Carl Zeiss e outros, cujos estudos resultaram na
introdução dos aperfeiçoamentos da mecânica de precisão nos instrumentos
topográficos. Ademais, os apefeiçoamentos na parte ótica dos instrumentos,
por Kepler, Porro, Zeiss e Wild; os avanços nas técnicas de medida direta
das distâncias, por Porro, Bessel e Jäderin; melhorias na precisão da leitura
de ângulos, devidas a Vernier, Nonius, Zeiss e Wild; os progressos nos
levantamentos topográficos devidos a Pothénot, Snellius, Hansen e na
avaliação mecânica das áreas devidas aos aparelhos Amsler, Coradi e
outros, deram à Topografia o valor que ela tem como ciência e como
técnica no levantamento topométrico preciso do terreno e na representação
gráfica equivalente, servindo como apoio de qualquer trabalho de
Engenharia e Agrimensura ( Espartel, op. cit.). Assim, o projeto de
qualquer obra de Engenharia, Arquitetura ou Agronomia, tem como
subsídio o prévio levantamento topográfico do lugar onde será implantada.

8. 2
A importância da Topografia fica evidente na boa administração das
terras públicas ou particulares, bem como no estudo, projeto e
planejamento das diversas atividades antrópicas, que exigem o
conhecimento do terreno, e este pode ser representado numa planta
topográfica com suas formas e dimensões, por meio de convenções pré-
estabelecidas sempre tendo em vista a escala da planta.

9. 3
2 TOPOGRAFIA
Etimologicamente o significado da palavra TOPOGRAFIA é
“descrição do lugar”. Segundo Mesquita ( 1969 ), a topografia pode ser
considerada um capítulo de uma área de conhecimento mais geral, a
GEODÉSIA, cujo objetivo é o estudo da forma e dimensões da Terra. A
Geodésia se ocupa dos processos de medida e especificação para o
levantamento da superfície de um Estado ou de um País, projetada sobre
uma superfície de referência que é a de um Elipsóide de Revolução. Este
Elipsóide, girando em torno de seu eixo menor, é a forma geometricamente
definida por dois parâmetros, mais próxima da figura da Terra
( Figura 01a ). As dimensões adotadas para o Elipsóide Internacional de
Referência são:
a = 6.378.388m ( semi-eixo maior ); b = 6.356.911,946m ( semi-eixo
menor )
3
2 ba +
= 6.371.229m ( raio médio ); oachatament
a
ba
f ==
−
=
297
1
O Geóide é a figura ideal caracterizada pela superfície de nível
médio dos mares prolongada através dos continentes. Esta superfície
prolongada, devido à Lei de Newton, da atração das massas, tende a elevar-
se em relação ao Elipsóide à medida que se aproxima e penetra nos
continentes, e a aprofundar-se à medida que se afasta dos continentes e
penetra nas bacias oceânicas.

10. 4
Topografia: até 50 Km de diâmetro
Figura 01a: Superfícies do Elipsóide, do Geóide e Topográfica (Mesquita, 1969 )
Em Topografia, o Geóide se confunde com o Elipsóide de
Referência, o qual se confunde com uma esfera osculadora regional cuja
superfície, numa extensão limitada, funde-se com a de um plano tangente
que é o Plano Topográfico.
A topografia é uma ciência aplicada de âmbito restrito, que se baseia
nos princípios da Geometria e da Trigonometria Plana.
2.1Levantamento Topográfico
Conjunto de operações de campo e escritório, necessários para a
representação de contornos de áreas e posição de pontos existentes na
superfície terrestre.
O levantamento topográfico pode ser:
A – Expedito: é um trabalho de reconhecimento da área, utilizando-se
aparelhos e instrumentos que conduzem à resultados de pouca precisão. O
levantamento expedito de um lote, por exemplo, consiste em efetuarmos a
medida de todos os seus lados com uma trena e balizas para não perdermos
o alinhamento no caso de mais de uma trenada para medida dos lados ou
das diagonais. Em seguida, medimos uma de suas diagonais. Com este

11. 5
procedimento obtemos as medidas dos lados de dois triângulos, o que
facilita a reprodução em escala, uma vez que um triângulo fica
perfeitamente identificado com o conhecimento das dimensões de seus três
lados ( Figura 01b).
Figura 01b: Levantamento expedito de um lote
No exemplo da Figura 01b, o lote ABCD teve os lados AB, BC, CD,
DA e a diagonal AC, medidos com uma trena. Com este procedimento o
quadrilátero ABCD fica dividido nos triângulos CDA e ABC. Com o
auxílio de um compasso, desenhamos os dois triângulos com o seguinte
procedimento:
a) Traçamos, na escala escolhida, o lado DC;
b) Com a ponta seca em D e abertura DA, traçamos um arco de
circunferência;
c) Agora com a ponta seca em C e abertura CA, traçamos outro arco de
circunferência que no cruzamento com o arco anterior determinará o
vértice A. Até aquí já temos o triângulo CDA;
d) Com a ponta seca em C e abertura CB traça-se novamente um arco de
circunferência;
e) Por fim, com a ponta seca em A e abertura AB, traçamos o arco de
circunferência que cruzará com o do ítem d determinando o vértice B. A
união de A com B e C com B, resultará no lote que foi medido.
B – Comum: é o mais utilizado nos trabalhos topográficos utilizando
aparelhos e instrumentos que conduzem a resultados de média precisão,
porém, suficiente para a grande maioria dos trabalhos de engenharia.
C – Precisão: é utilizado em alguns trabalhos especiais e, ainda, quando
tivermos com grandes áreas para levantamento.

12. 6
NBR 13133/94
Execução dos Levantamentos
Topográficos
2.2 Divisões da Topografia
A - Topometria
B - Topologia
A - Topometria: compreende o conjunto de operações necessárias a
obtenção de elementos indispensáveis a representação gráfica do terreno.
A.1 Planimetria: é a parte da topometria que estuda todas as projeções
dos contornos e pontos medidos que são representados em um plano
horizontal, sem considerar o relevo do terreno.
A.2 Altimetria: é a parte da topometria que trata do relevo da
superfície terrestre, onde são medidas as alturas dos pontos definidos pela
planimetria em relação à um plano de referência de nível. RN
B - Topologia: é a parte que se dedica ao estudo das formas do terreno
e das leis que regem seu modelado.
2.3 Partes de um Trabalho de Topografia
A ) Parte Matemática: Topometria com as medições de distâncias e
ângulos nos planos horizontal e vertical;
B ) Parte Interpretativa: Topologia com a descrição e interpretação das
diversas formas de relevo;
C ) Parte Artística: Desenho topográfico com a representação de todos os
detalhes do terreno, mediante convenções. Tais detalhes são: divisas, áreas
florestadas, rios, estradas, povoações etc.
O desenho de qualquer porção da superfície terreste, que
normalmente representamos em um papel, é sempre feito mediante a
utilização de um fator de redução que denominamos de ESCALA.
A ESCALA nada mais é que uma razão entre dimensão gráfica e dimensão
real, que analiticamente representamos por:
D
d
E = , onde: E = Escala; d = dimensão gráfica; D = Dimensão real.
A topometria se divide em duas partes:
A.1 Planimetria, e
A.2 Altimetria

13. 7
A razão
D
d
é usualmente utilizada nos cálculos para resolução de
problemas que envolvem escalas. Quando as dimensões gráficas e reais são
referentes a superfície ( área ) ou volume, a mesma expressão é utilizada na
resolução de problemas, porém elevada ao quadrado ou ao cubo
respectivamente, como por exemplo:
( )
A
a
E =
2
ou ( )
V
v
E =
3
, onde :
a = área gráfica, A = área real, v = volume nas dimensões do desenho, V=
volume nas dimensões reais.
Comumente representamos uma escala na forma de uma fração que
tem para numerador a unidade e para denominador o número que
representa quantas vezes a dimensão real, D, foi reduzida para poder ser
representada num papel de dimensão padronizada ( A2, A3, A4 etc...).
Todavia, também é frequente representar a escala na forma de divisão,
onde o primeiro número, a unidade, é separada do número redutor por dois
pontos, por exemplo:
250
1
=E ou E = 1:250, o que significa que cada centímetro no papel
representa 250 centímetros de dimensão real. Se este um centímetro no
papel for a extensão de uma parede, significa que a parede verdadeira, terá
250 centímetros de dimensão real, ou 2,50 metros.
Ao se procurar determinar uma escala a partir do conhecimento das
duas dimensões, d e D, é importante que ambas sejam escritas na mesma
unidade de medida, ou seja: se d for escrito em centímetro, D também
deverá sê-lo; se d, for escrito em milímetro, da mesma forma será D. Isto
porque a Escala é um número adimensional, isto é, não tem unidade.
As escalas também são representadas nas formas gráficas: simples e
de transversais.
A Figura 01c mostra uma escala gráfica simples, através da qual
podemos determinar imediatamente o comprimento real de um segmento
AB qualquer de uma planta mediante o seguinte procedimento: com um
compasso de ponta seca determina-se a abertura AB que comparada na
escala gráfica nos fornece diretamente o comprimento real. Na Figura 01c
este comprimento é de aproximadamente 13,4km.

14. 8
Figura 01c: Escala gráfica simples ( Mesquita, 1969 ).
A Figura 01d mostra uma escala gráfica de transversais. Nesta uma
distância AB qualquer em uma planta, comparada da mesma forma como a
anterior, com utilização de um compasso de ponta seca, será um tanto mais
precisa do que na escala gráfica simples. Na Figura 01d o segmento AB
corresponde a 13,46km. As escalas gráficas são muito utilizadas em
plantas, uma vez que fornecem a distância real de imediato.
Figura 01d: Escala gráfica de transversais ( Mesquita, 1969 )
2.4 UNIDADES DE MEDIDA
2.4.1 Medidas de Distância
Para medidas de distância a unidade padrão é o metro, com seus múltiplos
e sub – múltiplos que são:
múltiplos: km ( kilômetro ), hm ( hectômetro ), dam ( decâmetro );
sub-múltiplos: mm ( milímetro ), cm ( centímetro ), dm ( decímetro ).
km ←hm ←dam ←m →dm →cm →mm

15. 9
Ao fazermos a conversão de uma unidade para a outra que está
situada à sua direita, multiplicamos por dez cada vez que deslocamos até
chegar a unidade desejada, por exemplo: para fazermos a conversão de 25,2
hm para cm, deveremos multiplicar por dez quatro vezes até chegarmos em
cm, o que resulta em 252.000cm ou 25,2 x 104
cm.
Quanto se tratar de fazermos a conversão para uma unidade situada à
esquerda, o processo é semelhante, porém, ao invés de multiplicarmos,
dividimos por dez, por exemplo: para fazermos a conversão de 25,2cm para
hm, deveremos dividir por dez quatro vezes até chegarmos em hm, o que
resulta em 0,00252hm ou 25,2 x 10-4
hm.
2.4.2 Medida de superfície ( área )
Para medida de superfícies a unidade padrão é o metro quadrado com
seus múltiplos e sub-múltiplos que são:
km2
←hm2
←dam2
←m2
→dm2
→cm2
→mm2
Para conversão das unidades de superfície, o processo utilizado é similar
ao empregado para as unidades lineares, com a diferença que
multiplicamos e dividimos por 100, por exemplo: para fazermos a
conversão de 100cm2
em m2
, portanto para uma unidade da esquerda,
deveremos dividir por 100 duas vezes, isto é, por 10.000, o que resulta em
0,01m2
ou 100 x 10-4
m2
. No caso de convertermos 10hm2
em cm2
, portanto
para uma unidade situada à direita, multiplicaremos por 100 cinco vezes,
isto é, por 100.000.000, o que resulta em 1.000.000.000cm2
, ou 10 x
108
cm2
.
Outras unidades de medida de superfície são utilizadas em Topografia,
como o alqueire paulista, alqueire goiano e o hectare, as quais possuem a
seguinte equivalência:
1 alqueire goiano = 48.400m2
= 220m x 220m;
1 alqueire paulista = 24.200m2
= 110m x 220m;
1 hectare = ha = 10.000m2
= 100m x 100m.
O hectare ainda possui seus sub-múltiplos que são o are = 100m2
e o
centiare = 1m2
.

16. 10
2.4.3 Medida de volumes
Para medida de volumes a unidade padrão é o metro cúbico com seus
múltiplos sub-múltiplos que são:
km3
←hm3
←dam3
←m3
→dm3
→cm3
→mm3
Para conversão de uma unidade de volume em outra, usa-se o mesmo
processo utilizado para as unidades lineares e de superfície, diferindo na
multiplicação e divisão que neste caso será por 1.000 cada vez que nos
deslocamos para chegarmos na unidade desejada.
2.4.4 Medida de massa
A unidade padrão para medida de massa é o grama com seus múltiplos e
sub-múltiplos que são:
kg ←hg ←dag ←g →dg →cg →mg
Para conversão de uma unidade de massa, o procedimento é o mesmo
empregado nas unidades lineares, isto é, ao passarmos para uma unidade à
direita multiplicamos por 10, e dividimos por 10 quando se tratar de passar
para uma unidade da esquerda, tantas vezes quantas forem necessárias para
atingirmos a unidade desejada.
Finalizando, observa-se que a conversão de uma unidade resume-se a
um processo de multiplicação e divisão por potências de dez.
É importante observar, também, que tanto os múltiplos quanto os sub-
múltiplos de unidades de medidas são precedidos de um prefixo indicativo
de potência de dez. Os prefixos normalmente utilizados e as respectivas
potências de dez que indicam são os seguintes:
Prefixos indicativos de expoentes negativos de base 10
Deci = 10-1
Centi = 10-2
Mili = 10-3
Micro = 10-6
Nano = 10-9
Pico = 10-12
Femto = 10-15
Atto = 10-18
Prefixos indicativos de expoentes positivos de base 10
Deca = 10 Hecto = 102

17. 11
Kilo = 103
Mega = 106
Giga = 109
Tera = 1012
Peta = 1015
Exa = 1018
2.4.5 Medidas de Ângulos
A. Sistema Centesimal de divisão de áreas
B Sistema Sexagesimal de divisão de arcos
C Radiano: unidade de medida de ângulo central que subentende um
arco de circunferência de comprimento igual ao raio. Assim podemos
escrever:
A circunferência se divide em 400 parte iguais chamadas
de Grade, que por sua vez se divide em 100 partes iguais
(minuto), que por sua vez se divide em 100 partes iguais
(Segundos).
A circunferência se divide em 360
partes iguais chamado de Grau, que
por sua vez se divide em 60 partes
(minutos) e por sua vez se divide em
60 partes (segundos).
10
= 60’
1’ = 60”

18. 12
R
S
=θ , onde S = comprimento do arco de circunferência subentendido pelo
ângulo central; R = raio da circunferência.
Para θ = 1 radiano, temos: S = R. Uma circunferência completa tem 2πrad.
D Milésimo: Por curiosidade, é uma unidade de medida de ângulo
que foi muito usada nos equipamentos de pontaria de peças de artilharia
antigas. Corresponde à milésima parte do radiano e, portanto, uma
circunferência completa tem 6.400 milésimos.
Desta forma, temos a seguinte equivalência entre as unidades:
360o
= 400 grd = 2πrad = 6.400 milésimos, ou dividindo tudo por 2:
180o
= 200 grd = πrad = 3.200 milésimos, o que permite a conversão de
unidades.
EXERCÍCIOS
1 ) Qual a largura, em planta na escala 1:200, do leito carroçável de 10
metros de largura de uma estrada?
2 ) Em uma planta na escala 1:250, dois pontos A e B, estão afastados de
40cm. Qual a distância real entres eles?
3 ) Um prédio possui um volume de 4.000 m3
. Qual o volume deste mesmo
prédio, em cm3
, ao ser reduzido na escala de 1:200?
4 ) Em uma planta na escala de 1:500, um terreno apresenta 4cm de frente
por 8cm de fundo. Qual a área do terreno em ha?
5 ) Dois pontos, A e B, em uma planta cuja escala desejamos saber, estão
afastados de 40cm. A distância real entre eles é de 4 km. Qual a escala da
planta?

19. 13
6 ) A testada de um lote é de 20m. A dimensão gráfica é de 2cm. Qual a
escala da planta e qual a dimensão gráfica em uma planta na escala
1:2.000?
7) O milésimo é uma unidade de medida de ângulo empregada em cálculos
militares. Corresponde a abertura angular resultante da paralaxe de 1 metro
a 1.000 metros de distância. Uma circunferência completa tem 6.400
milésimos. Tomando como base estas informações, qual a distância de um
observador em relação a uma tôrre de 40 metros de altura, vista sob um
ângulo de 8 milésimos?
8 ) Um lote com as dimensões de 20 metros de frente por 40 metros de
fundo, deverá ser representado em uma planta na escala 1:2.000. Quais as
dimensões deste lote na planta, em centímetros?
9 ) Os Marcos quilométricos 240 e 242 de uma rodovia, distam 20 cm em
uma planta. Em uma outra planta, na mesma escala, a distância real entre
duas casas é de 6km. Qual a distância gráfica entre elas?
10 ) Qual a área real de um terreno de 10cm x 30cm representado em uma
planta na escala 1:2.500?
2.5 MEDIÇÃO DE ÂNGULOS
Em topografia, considera-se somente a medida dos ângulos contidos
em dois planos: horizontal, nas operações de planimetria, e o vertical nas
operações de altimetria.
Os ângulos contidos no plano horizontal, por isso chamados de
horizontais, de acordo com a direção ou alinhamento que serve de origem

20. 14
para a sua medida, classificam-se em AZIMUTAIS e
GONIOMÉTRICOS.
2.5.1 ÂNGULOS AZIMUTAIS
São ângulos que possuem como origem a direção da linha Norte -
Sul. Estes ângulos são denominados de : RUMOS E AZIMUTES. A linha
Norte-Sul é o meridiano local, isto é, aquela que une o polo Norte com o
polo Sul terreste. Neste caso temos os azimutes e rumos verdadeiros ou
geográficos. Quando esta linha Norte-Sul é aquela que une os polos Norte e
Sul magnéticos, temos os azimutes e rumos magnéticos que podem ser
obtidos com uma bússola. É importante salientar que as linhas Norte-Sul
verdadeira e magnética, dependendo da nossa posição na superfície
terreste, formam um ângulo entre si denominado de declinação magnética.
A declinação magnética, portanto, é o ângulo formado entre os
alinhamentos Norte-Sul verdadeiro e Norte-Sul magnético medido a partir
da extremidade do Norte verdadeiro no sentido da extremidade do Norte
magnético. Ela pode ser positiva ( declinação para LESTE ) ou negativa
( para OESTE ), isto é, quando o Norte magnético estiver a leste do
verdadeiro ou a oeste respectivamente ( Figura 01d ).
Figura 01e: Declinação magnética negativa (a) e positiva (b).

21. 15
Por outro lado, a declinação magnética varia anualmente. Assim, nos
trabalhos de topografia em que há necessidade de converter rumos e
azimutes magnéticos em verdadeiros ou geográficos, é necessário que
saibamos qual a sua variação anual na região objeto do levantamento. Esta
operação de atualização da declinação é chamada de “reaviventação”.
A reaviventação pode ser feita através da seguinte expressão:
δa t = δp + δan . ∆t, onde:
δat = declinação atual;
δp = declinação passada;
δan = variação anual;
∆t = intervalo de tempo.
Assim, por exemplo, se a declinação em uma determinada região era
de 10o
25’para oeste, no ano de 1969, com variação anual de 10’, a sua
declinação em 1999 ( δat ) será:
δat = δp + δan.∆t
δat = 10o
25’+10’x 30 = 15o
25’ para oeste ou (–)10o
25’.
A RUMOS
Rumo é o menor ângulo formado entre o alinhamento e a linha Norte
- Sul, medido a partir do Norte ou do Sul e variando de 0º à 90º
. É
representado por R. Para que este ângulo fique determinado é necessário
indicar o quadrante no qual o alinhamento se encontra. Quando a linha
Norte-Sul é a verdadeira ou geográfica, temos os rumos verdadeiros ou
geográficos; quando é a magnética, temos os rumos magnéticos.

22. 16
N 2 N
2
R1,2
3
1 N R2,3
IV (NW) I (NE)
W E
III (SW) II (SE)
S
EXEMPLOS
N B N
C
20º
35º
A
RA,B=20º
(NE) D RC,D=35º
(SE)
B AZIMUTES
Azimutes são os ângulos formados entre o alinhamento e a linha
Norte - Sul, medido a partir do Norte em sentido horário e variando de 0º
à
360º
e é representado por Az. Quando a linha Norte-Sul é a verdadeira ou
geográfica, temos os azimutes verdadeiros ou geográficos; quando é a
magnética, temos os azimutes magnéticos.
Quadrantes topográficos:

23. 17
N N d N
a Az a,b e
Az c,d Az e,f
c
b f
B.1 CONTRA – AZIMUTE ou AZIMUTE À RÉ
Contra – Azimute é o azimute em sentido contrário ao alinhamento.
N
1 N
2
B.2 Relações Existentes entre Azimute e Contra – Azimute
N
1º Quadrante (NE)
N
2
1
Az 1,2
CAz1,2 = Az 2,1
CAz = Az 1,2+180º

24. 18
2º Quadrante (SE)
3
4
3º Quadrante (SW) N
5
N
6
4º Quadrante ( NW )
N
N
8
7
Quando o azimute de um for menor que 180º o
CAz será Az+180º. Quando o Azimute for
maior que 180º o CAz será o Az – 180º.
CAz = Az 5,6-180º
CAz = Az 3,4+180º
CAz = Az 7,8-180º

25. 19
EXERCÍCIOS
1 ) Transformar em Rumos (R) os Seguintes Azimutes (AZ)
a-)Az1,2 = 45º10’20’’
R: R1,2 = 45º10’20’’ 1º Quadrante (NE)
b-)Az2,3 = 90º
R: R2,3 = 90º (E)
c-)Az3,4 = 360º
R: R3,4 = 0º
d-)Az4,5 = 225º40’
R: R4,5 = 225º40’ – 180º = 45º40’ 3º Quadrante (SW)
e-)Az5,6 = 270º
R: R5,6 = 90º (W)
f-) Az6,7 = 305º30’20’’
R: R6,7 = 54º29’40’’ 4º Quadrante (NW)
2 ) Calcular os Contra – Azimutes (CAz) dos azimutes dados abaixo:
a-) Az1,2 = 40º20’10’’
R: CAz = Az + 180º = 40º20’10’’+180º = 220º20’10’’
b-) Az2,3 = 360º
R: CAz = Az – 180º = 360º – 180º = 180º
c-) Az3,4 = 181º10’20’’
R: CAz = Az – 180º = 181º10’20’’ – 180º = 1º10’20’’
d-) Az4,5 = 0º
R: CAz = Az + 180º = 0º + 180º = 180º
3 ) A leitura de um azimute efetuada com um teodolito graduado em
radianos, foi de 5 rad. Qual seria a leitura em graus, minutos e segundos?
4 ) O leito carroçável de uma rodovia tem a largura de 7.000mm. Qual a
sua largura em km, hm, dam e metro?
5 ) O ângulo de uma rampa é de 30o
50’45”. Qual o ângulo desta rampa em
grados?

26. 20
6 ) O perfil de um lote apresenta uma declividade em que a sua altura varia
de 1metro a cada metro de caminhamento na horizontal. Qual o seu ângulo
de rampa ( ângulo formado com a horizontal )?.
7 ) A quantos Gigametros corresponde o Nanometro?
8 ) Uma circunferência completa tem 6400 milésimos ( unidade de medida
de ângulo usada para fins militares ). Com base nesta informação, qual o
ângulo em milésimos correspondente a 250 grd?
9 ) Para implantação de uma obra foi efetuada uma escavação de 1.000 cm
de largura, 40.000 mm de comprimento e 0,025 hm de profundidade. Qual
o volume de material retirado, em metros cúbicos?
10 ) Um recipiente possui um volume de 2,5 hl. Qual o peso deste volume,
em hg, tratando-se de água a 4o
C?
11) Em uma planta na escala 1:2.500, a largura de um terreno é de
0,00002km. Se o comprimento real do terreno for de 100.000mm, qual é a
área real do terreno em hectares?
12 ) Na locação de um ponto, distante 2km de uma estaca, foi cometido um
erro angular de 1”. Qual o deslocamento ocorrido na locação do ponto e
qual o erro relativo cometido nesta operação?
2.5.2 ÂNGULOS GONIOMÉTRICOS
Definição: são ângulos que possuem como origem um alinhamento
qualquer. Classificam-se em : ângulo de flexão ou ângulo entre
alinhamentos e ângulo de deflexão...

27. 21
A. FLEXÃO
É o ângulo formado entre dois alinhamentos consecutivos e variável
de 0º à 360º.
Exemplo:
1 3
2
B. DEFLEXÃO
É o ângulo formado entre o prolongamento do alinhamento à ré e o
alinhamento à vante variando de 0º à 180º.
Exemplo:
1 3
2
3 1
2
α2
α’2
d2
d2

28. 22
C. SENTIDO DOS ÂNGULOS GONIOMÉTRICOS
Os ângulos goniométricos poderão ser à direita ou à esquerda do
alinhamento. Por convenção, o ângulo será à direita ou positivo (+) quando
medido no sentido horário do alinhamento à ré para o à vante e, será à
esquerda ou (-) quando medido em sentido anti - horário do alinhamento à
ré para o à vante.
2.5.3 ÂNGULOS AZIMUTAIS X ÂNGULOS GONIOMÉTRICOS
Poligonal Topográfica é uma seqüência de
alinhamentos, podendo ser aberta, fechada ou apoiada.
Exemplos
1 3
2 4
1 2 1 2
6
5
4 3 4 3
Aberta
Fechada
Apoiada

29. 23
2.5.4 CÁLCULO DE RUMOS E AZIMUTES A PARTIR DE ÂNGULOS
GONIOMÉTRICOS
1 3
2 4
1 3
2 4
Az2,3=Az1,2 – ββββ
ββββ = 180º – αααα2Az23 =
Az23 =Az12 – (180º – αααα2)
Az23 = Az12 – 180º + αααα
Az12
α2
d3
Az12
α2
Az23=?
Az12
180º
β

30. 24
EXERCÍCIO
Calcular os Az e R das linhas que formam a poligonal a seguir:
B E F
A C D G
B
A C
RBC = RB,A-40°15’05’’
RBC = 20°15’05’’ (SE)
AzAB= 180° - RAB = 180° −= 180° −= 180° −= 180° − 60°30’10’’ = 119°29’50’’
AzBC= 180° - RBC = 159°44’55’’
40°15’05’’
152°40’20’’
272°05’07’’
210°25’03’’
85°10’20’’
R A,B=60°30’10’’
Az
40°15’05’’
RAB=60°30’10’’(SE)
RBA=60°30’10’’(NW)
119°29’50’’
RB,C

31. 25
B D
A C
AzCD= AzBC - ββββ ( ββββ = 180° – 152°40’20’’ = 27°19’40’’ = ββββ =27°19’40’’)
AzCD= 180° - β = 159β = 159β = 159β = 159°44’55’’ −−−− 27°19’40’’ = 132°25’15’’
RCD = 180° - AzCD = 47°34’45’’ (SE)
E
F
D
C
AzDE = AzCD – ββββ (ββββ = 210°25’03’’ – 180° = 30°25’03’’ = ββββ)
AzDE = AzCD – ββββ = 132°25’15’’ – 30°25’03’’ = 102°00’12’’
RDE = 180° - AzDE = 77°59’48’’ (SE)
AzCD
180º
152°40’20’’
AzBC = 159°44’55’
β
RCD
RCD
210°25’03’’
β
180°
AzDE
RDE

32. 26
E
F
AzEF = ββββ + AzDE (ββββ = 272°05’07’’ – 180° = 92°05’07’’ = ββββ)
AzEF = AzDE + ββββ = 102°00’12’’ + 92°05’07’’ = 194°05’19’’
REF = AzEF – 180° = 14°05’19’’(SW)
2.5.4.1 FÓRMULA GERAL DOS AZIMUTES
A. Fórmula Geral para Ângulos de Flexão
1 3
2 4
Az2,3 = Az1,2 – ββββ
ββββ = 180° – αααα2 Az2,3 = Az1,2 + αααα2 – 180°
Az1,2
α2
Az1,2
Az2,3
α3
Az2,3
Az3,4
272°05’07’’
AzEF
β
REF
RED

33. 27
Az3,4 = Az2,3 + ββββ’
ββββ’ = 180° - αααα3 Az3,4 = Az2,3 – αααα3 + 180°
Azn = Azn-1 + ααααn + 180°
QUANTO AOS SINAIS
Do ângulo de flexão α
Será positivo α quando este ângulo for à direita
Será negativo α quando este ângulo for à esquerda
Do ângulo de 180°
Será positivo 180° quando o azimute anterior + αn for menor que 180°
Será negativo 180° quando o azimute anterior + αn for maior que 180°
Azimute da linha
em questão
Azimute da
linha anterior
Ângulo de flexão no
vértice inicial da linha
em questão

34. 28
B. Fórmula Geral para Ângulos de Deflexão
1 3
2 4
Az2,3 = Az1,2 – d2
Azn = Azn-1 + dn
Az3,4 = Az2,3 + d3
2.5.5 Limites do Azimute
Como o azimute é um ângulo que varia de 0° à 360°, então quando
ocorrer valor para o azimute maior que 360°, este valor deverá ser
subtraído de 360° e, quando ocorrer valor menor que 0° então, o valor
deverá ser acrescido em 360°.
d2
d3
Az1,2
Az1,2
Az2,3
Az2,3
Az3,4

35. 29
EXERCÍCIO
Calcule os azimutes das linhas poligonais abaixo.
1
3 2 0
5
4 6
Az0,1 = 73°50’30’’
Az1,2 = 73°50’30’’ – 75°45’12’’ = 358°05’18’’
Az2,3 = 358°05’18’’ – 140°53’08’’ – 180° = 37°12’10’’
Az3,4 = 37°12’10’’ – 280°42’18’’ + 180° = – 61°30’ + 360° = 296°29’52’’
Az4,5 = 296°29’52’’ + 89°20’35’’ – 180° = 205°50’27’’
Az5,6 = 205°50’27’’ + 31°15’03’’ = 237°05’30’’
Az6,0 = 237°05’30’’ + 102°15’ – 180° = 159º20’30’’
75°45’12’’
280°42’18’’
94°30
140°53’08’’
89°20’35’’ 31°15’03’’
102°15’

36. 30
Linhas Az CAz R
0 – 1 73°50’30’’ Az+180°=253°50’30’’ 73°50’30’’ (NE)
1 – 2 358°05’18’’ Az-180°=178°05’18’’ 360°-Az=1°54’42’’(NW)
2 – 3 37°12’10’’ Az+180°=217°12’10’’ 37°12’10’’(NE)
3 – 4 296°29’52’’ Az-180°=116°12’10’’ 360°-Az=63°30’08’’(NW)
4 – 5 205°50’27’’ Az-180°=25°50’27’’ Az-180°=25°50’27’’(SW)
5 – 6 237°05’30’’ Az-180°=57°05’30’’ Az-180°=57°05’30’’(SW)
6 – 0 159°20’30’’ Az+180°=339°20’30’’ 180°-Az=20°39’30’’(SE)
EXERCÍCIOS
1 ) Em maio de 1958 foi efetuado um levantamento topográfico de uma
propriedade pelo método do caminhamento perimétrico, no sentido
horário, numa região cuja declinação magnética era de +9o
15’ com
variação anual de +5’. O azimute magnético à ré lido do vértice 2 para o
vértice 1 ( Azm 2,1 ) foi de 194o
02’ 33’’ ; o ângulo de flexão (-) no vértice 2
foi de 113o
29’10”; o ângulo de deflexão (+) no vértice 3 foi de 119o
06’10”; o azimute magnético à ré do vértice 1 para o vértice 4 foi de 94o
30’30”.
Com relação ao levantamento efetuado, pede-se:
1 ) Calcular todos os azimutes vante verdadeiros: Azv1,2, Azv 2,3, Azv 3,4,
Azv 4,1 . ( 2,0 )
2 ) Calcular todos os ângulos de flexão (-). ( 2,0 )
3 ) Calcular todos os contra-azimutes verdadeiros. ( 1,5 )
4 ) Calcular todos os rumos vante e ré verdadeiros. ( 1,5 )
5 ) Calcular a soma dos ângulos internos da poligonal. ( 1,5 )
6 ) Fazer um esboço da poligonal levantada. ( 1,5 )

37. 31
2.6 Medidas de Distância
A determinação da extensão de um alinhamento pode ser feita por
medida direta, quando o instrumento de medida é aplicado no terreno ao
longo do alinhamento, por medida indireta, se em função da medida de
outras grandezas com ela relacionada matematicamente, ou por medida
eletrônica, realizada com instrumentos que utilizam raios infravermelhos
ou a laser permitindo a determinação das distâncias com rapidez e precisão
(Distanciômetro).
2.6.1. Medida Direta – Processos
Nos processos para medida direta de distâncias, o instrumento
aplicado ao longo do alinhamento a medir denomina-se diastímetro.
De acordo com a natureza do diastímetro e grau de precisão desejado
para a medida, os processos de medida direta classificam-se em:
A)- Processos de Baixa Precisão
B)- Processos de Média Precisão
C)- Processo de Alta Precisão
A Processo de Baixa Precisão
São os processo que conduzem a resultados com baixo grau de
precisão. São empregados nos trabalhos de reconhecimento, levantamentos
rápidos onde não se exige grande precisão (levantamentos expeditos). Os
diastímetros utilizados são: Passo humano, passômetro, velocímetro, etc.

38. 32
B Processos de Média Precisão
Nesta categoria se processam as medidas executadas nos trabalhos
normais de topografia.
Além do instrumento de medida, vamos empregar alguns
instrumentos auxiliares; tais como:
Piquetes ou estacas, servem para sinalizar a origem e o fim dos
alinhamentos, os vértices das poligonais, a origem e o fim das
curvas, etc.
Estacas testemunhas, servem para identificação rápida do piquete e
devem ser cravadas a 0,5 metros do piquete.
Balizas, servem para o operador do teodolito realizar a rápida
visualização do piquete; serve para fixar o plano vertical que contém
um alinhamento.
O diastímetro utilizado para medida direta do alinhamento com média
precisão é a “trena”, podendo ainda ser utilizada a “fita de aço”.
C Processos de Alta Precisão
São utilizados na medição das bases geodésicas ( lados dos
triângulos geodésicos ) . Empregam-se os distanciômetros eletrônicos
baseados na propagação de micro-ondas ou de ondas luminosas. Entre os
que emitem micro-ondas temos os telurômetros, cujo alcance chega a
160km com precisão de 5cm ±3:1.000.000. Na classe dos que emitem
ondas luminosas temos o Geodímetro com alcance de 60km e precisão de
6mm±1:1.000.000, e o Geodolito com alcance de 32km nas medições
diurnas e 80km nas medições noturnas ( T34-400 ).

39. 33
2.6.2 Técnica de Medida com Trena
Para que a distância entre dois pontos seja medida com precisão, a
trena dispor-se-á horizontalmente e estará contida no plano vertical que
contém o alinhamento.
Ao operador e seus auxiliares compete cuidar da horizontalidade da
trena e da verticalidade da baliza no momento da medida.
O plano vertical poderá ser materializado com o emprego de balizas
e um instrumento óptico (teodolito) através da operação denominada
balizamento.
Suponhamos que se deseje medir o cumprimento “L”, com uma trena
a partir do ponto “A” até o ponto “B” fixado no terreno. Um auxiliar deverá
por uma baliza no ponto “A”, mantendo o zero da trena junto ao eixo da
baliza disposta verticalmente; outro auxiliar deverá ir desenrolando a trena
até a de marca “L metros”. Os auxiliares dos pontos A e B se colocam atrás
das respectivas balizas, quando o operador do teodolito orientará os
auxiliares para que fiquem na mesma direção, ou seja, no mesmo plano
vertical que contém o alinhamento AB e, ainda orientará para que a trena
fique disposta na horizontal. Então, neste momento, farão a medida do
alinhamento.

40. 34
2.6.3 Técnica de Medidas Indiretas

41. 35
EXEMPLO
2.7 MÉTODO DE LEVANTAMENTO TOPOGRÁFICO
2.7.1. Método do caminhamento perimétrico ou método da poligonal
Consiste na ligação dos pontos 2 a 2, da poligonal a ser levantada, através
da medição de ângulos e distâncias em cada vértice da poligonal.
Vantagens:
Pode ser usado em qualquer área, desde que os pontos sejam acessíveis.
Desvantagens:
Método demorado e trabalhoso. Proporciona grande acúmulo de erros.

42. 36
Em áreas extensas combinam-se o método com o GPS
GPS – Global Positioning System: Sistema de Posicionamento Global
Segundo Barros (1995 ) o Sistema de Posicionamento Global foi
idealizado pelo Departamento de Defesa dos Estados Unidos. Consiste em
uma constelação de 21 satélites em grandes altitudes. Este conjunto de
satélites substitui as estrelas até então usadas pelo homem para navegação.
O seu custo foi por volta de US$ 10 bilhões. O princípio básico do Sistema
consiste em utilizar satélites como pontos de referência para triangular
nossa posição em algum lugar da Terra, isto é, a nossa posição é conhecida
através da medição da distância de onde nos encontramos sobre a superfície
da Terra, até um grupo de satélites no espaço.
Assim, por exemplo, se sabemos que estamos a uma distância de 18.000km
de um satélite A, temos uma posição específica dentro do Universo que é
no interior de uma esfera com raio conhecido e com centro no satélite A
( Figura 01f). Conhecendo a nossa distância em relação a um outro satélite
B, por exemplo de 20.000km, a nossa posição fica melhor definida.
Portanto, o único lugar do Universo onde podemos estar a 18.000km do
satélite A e 20.000km do satélite B é no círculo formado pela interseção
das duas esferas ( Figura 01g).
Figura 01f: Um satélite Figura 01g: Dois Satélites

43. 37
Obtendo-se uma medida de distância a um terceiro satélite, 15.000km por
exemplo, podemos determinar realmente a nossa posição, uma vez que o
lugar geométrico que a define são apenas dois pontos: a interseção do
círculo formado pelos satélites A e B com a esfera do satélite C ( Figura
01h).
Figura 01h: Três Satélites
2.7.2 Método da Irradiação
3
2 4
1 5
Consiste em se fazer visadas de um ponto chamado sede da irradiação, para
os demais pontos da poligonal, ou pontos de detalhes, medindo-se os
ângulos e as distâncias formadas entre a sede da irradiação e os pontos
Sede da
Irradiação
Azimutes
Norte
Magnético
Distâncias

44. 38
visados. Este método poderá ser utilizado para levantamento de áreas e
para levantamento dos pontos de detalhes.
Vantagens:
Método rápido e de fácil execução
Desvantagens:
Não possibilita a verificação dos erros cometidos
É um método restrito, utilizado somente em áreas que permitam a
visualização de todos os seus vértices a partir de um ponto (sede da
irradiação), e ainda, que não seja extrapolado o alcance máximo da
luneta no momento das visadas.
2.7.3 CÁLCULO DA POLIGONAL
A Poligonal Aberta
3
1
4
2
Poligonal aberta é aquela que não retorna ao ponto de partida, não
possibilitando a verificação de erros, cometidos no campo.
Az1,2
α2
α3
L1,2
L2,3 L3,4

45. 39
A.1 CÁLCULO DAS COORDENADAS DOS PONTOS
y
N
y3
y2
x
x2 x3
X2 e Y2 serão coordenadas arbitradas ou conhecidas
FÓRMULA NO EIXO X
FÓRMULA NO EIXO Y
Az2,3L2,3
L2,3 x
Az2,3
23
23
23
L
xL
SenAZ =
L2,3X = L2,3SenAz2,3
X3 = X2 + L2,3X
L2,3Y = L2,3 CosAz2,3
Y3 = Y2 + L2,3Y

46. 40
EXERCÍCIOS
Calcular as coordenadas dos vértices da poligonal a seguir
Lado Comprimento
do lado
Azimute Projeção natural
dos lados
Vértice
Coordenadas
LX LY X Y
1 – 2 57,60 100°50’ 56,573 -10,826 1 500,0 500,0
2 – 3 42,35 43°20’ 29,062 30,804 2 556,573 489,174
3 – 4 59,43 124°45 48,830 -33,874 3 585,635 519,978
4 634,465 486,104
Az1,2 = 100°50’
α2 = 237°30’
α3=98°35’
L1,2 = 57,60
L2,3 = 42,35
L3,4 = 59,43
Comprimento do
lado vezes SenAz
Comprimento do
lado vezes CosAz
LxXnXn ±−= 1
LyYnYn ±−= 1

47. 41
A.2 Regras para correção dos ângulos internos
1.Todo Polígono fechado
Se o erro de campo for menor que o erro admissível, então distribuir.
Se o erro de campo for maior que o erro admissível, retornar para o campo
e medir novamente.
B Poligonal Fechada
Erro Linear = Ef
Detrminação do Erro linear de fechamento
2
1
5
3
4
Ec = erro de campo
ÂI = Ângulos Internos
Ead = erro admissível
pa = precissão angular do aparelho
npaead =
n = número de
vértices da poligonal
0
180).2(.. −=∑ nIntÂng
0
180).2()( −−∑= ncampoÂIEc
Ef
Efx
Efy
22
yExEE fff +=

48. 42
Determinação da projeção Efx e Efy
Teorema de Thales
A soma algébrica das projeções dos lados de um polígono qualquer
sobre uma reta orientada é sempre nula, quando a extremidade do último
lado coincide com a origem do primeiro.
B
A
C
D
Então temos: quando Σx≠0 temos Efx e,
Σy≠0 temos Efy.
B.1 Cálculo do erro linear relativo = Er
,
1
M
Er = sendo
fE
p
M
2
=
Onde 2p é o perímetro da poligonal
Ef é o erro linear de fechamento
São aceitos os seguintes limites de tolerância do erro linear de fechamento:
Terreno Plano 1:2000
Terreno Ondulado 1:1000
Terreno Acidentado 1:500
0
0
0
0
=∑
=∑
=+++
=+++
y
x
yyyy
xxxx
DACDBCAB
DACDBCAB

49. 43
B.2 Cálculos dos Fatores de Correção
Onde l = lado a ser corrigido.
EXERCÍCIO
Calcular as coordenadas da poligonal dada a seguir:
0 3
1
2
pa=6’’ X1=1.000,00m Y1=2.000,00
107°44’10’
72°43’30’’
88°41’40’’
90°50’32’’
l
p
xE
C
l
p
xE
C
f
y
f
x
.
2
.
2
=
=

51. 45
B.3 CÁLCULO DA ÁREA DE POLIGONAIS FECHADAS
ATRAVÉS DAS COORDENADAS DOS SEUS VÉRTICES
0
N0
N1 1
2
N2
E0 E2 E1
B.3.1 Fórmula de Gauss
S – área da
poligonal

52. 46
AB
Além dos métodos já estudados (Irradiação e Caminhamento
Perimétrico), outros métodos também são importantes e aplicados, muitas
vezes, em casos particulares de levantamento.
2.7.4 Método da Interseção
É bastante utilizado quando o ponto a determinar é inacessível. Ex:
um ponto situado dentro de um rio.
Consiste na determinação da posição de um ponto pela interseção
das visadas feitas das extremidades de um alinhamento, denominado
BASE, para este ponto.
M
A B
AzA,B
AzA,M
AzB,A
AzB,M
αA
αM
αB
Do campo: AB ; AzA,M, AzA,B, AzB,M, AzB,A

53. 47
Da Lei dos Senos:
Calcula-se αA, αB e αM:
Coordenadas do Ponto M a partir do ponto A
XM = XA + AM . Sen AzA,M
YM = YA + AM . Cos AzA,M
Coordenadas do Ponto M a partir do ponto B
XM = XB + BM . Sen AzB,M
YM = YB + BM . Cos AzB,M
)(1800
,,
,,
BAM
AzAzB
AzAzA
abmb
maba
ααα
α
α
+−=
−=
−=
m
b
Sen
Sen
AB
AM
α
α
=
m
b
Sen
Sen
ABAM
α
α
.=
m
a
Sen
Sen
AB
BM
α
α
= m
a
Sen
Sen
ABBM
α
α
.=

54. 48
EXERCÍCIOS
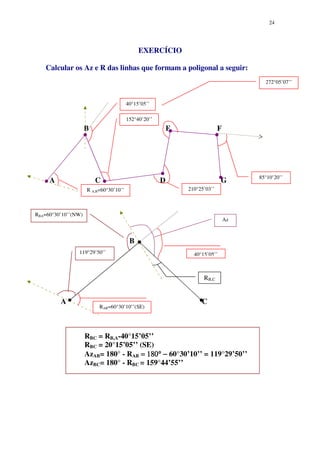
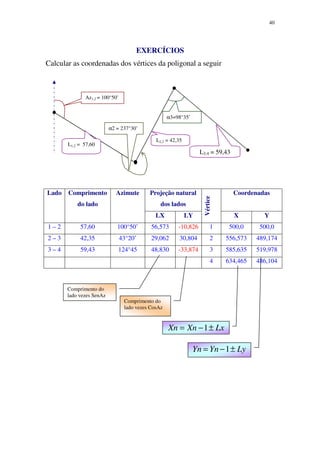
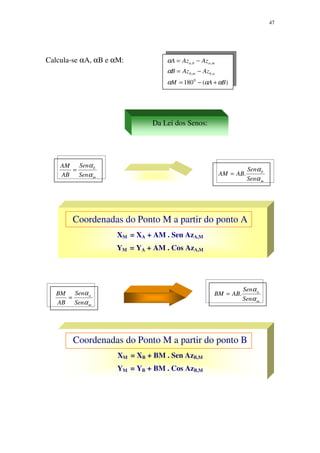
1 ) Calcular as coordenadas do ponto M levantado por interseção a partir da base AB
definida por RA,B = 72°30’ (NE); AB = 418,40; XA = 500m; YA = 700m. Tendo sido
medidos RA,M = 42°20’ (NE) e RB,M = 50°45’(NW).
Resolução:
RA,B = 72°30’ (NE) XA = 500m
AB = 418,40m YA = 700m
Foram medidos no campo:
RA,M = 42°20’ (NE) RB,M = 50°45’(NW)
M
A B
αA = (RA,B) 72°30’ – (RA,M ) 42°20’ = 30°10’
αB = 180° - [(RB,M) 50°45’+(RA,B) 72°30’] = αB = 56°45’
αΜ = 180° – (αA) 30°10’ + (αB) 93°05’ = αM = 93°05’
Coordenadas do Ponto M
XM = XA + AM .Sen AzA,M ⇒ 500+350,40939.Sen 42°20 = 735,98064
YM = YA + AM .Cos AzA,M ⇒ 700 + 350,40939.Cos 42°20 = 959,0364
RA,B = 72°30’
RA,M = 42°20’
50°45’(NW)
RB,A = 72°30’
αA = 30°10’
αM = 93°05’
αB = 56°45
m
b
Sen
Sen
ABAM
α
α
.= 40939,350
'0593
'4556
.40,418 0
0
==
Sen
Sen
AM

55. 49
2 ) As coordenadas do vértice no. 2 de uma poligonal são: W = 20m; N =
40m, em relação a um referencial no vértice no. 1. Qual o azimute 1-2
( Az1-2 )?
3 ) O perímetro de um terreno é uma circunferência de raio igual a 50
metros. Qual o comprimento de uma parte deste perímetro subentendida
por um ângulo de 0,5 radianos?
4 ) Qual a área, em alqueires paulista, de uma poligonal cujo levantamento
topográfico resultou nas seguintes coordenadas para os vértices?
Vértice 1 ( 202 Este; 300 Norte );
Vértice 2 ( 250 Este; 315 Norte );
Vértice 3 ( 240 Este; 290 Norte );
Vértice 4 ( 210 Este; 250 Norte ).
5 ) A declinação magnética de uma determinada região, objeto de um
levantamento topográfico, é de –10o
25’ em 31/07/1980. A variação anual
desta declinação é de –5’. Qual será o azimute verdadeiro ou geográfico
referente ao azimute magnético de 20o
30’ lido em 30/06/1997?
6 ) Utilizando-se o alinhamento C-D coincidente com o meridiano local, e
C distante de D 300 metros, estacionou-se o teodolito em C obtendo-se os
azimutes Azca e Azcb de 240o
e 120o
respectivamente. Em seguida, com o
teodolito estacionado em D, obteve-se os azimutes Azda e Azdb de 290o
e
25o
respectivamente.
Com base no procedimento de campo acima descrito, responda as seguintes
questões:
A ) Qual é a distância A-B?
B ) Qual é a distância A-D?
C ) Qual é a distância D-B?
7 ) Com um teodolito estacionado em uma estaca 1, foi determinado o
azimute 1-3 ( Az1-3 ) de 70o
, sendo o ponto 3 inacessível. Ainda com o
teodolito estacionado na estaca 1, foi lido o azimute 1-2 ( Az1-2 ) de 120o
e
determinada a distância 1-2 de 254,50 metros. Em seguida o teodolito foi
estacionado na estaca 2 e lido o azimute 2-3 ( Az2-3 ) de 10º
. A altitude da
estaca 1 é de 702,50m e a altura do aparelho, quando estacionado na estaca
1 era de 1,60m e em 2 de 1,62m. Os ângulos verticais 1-2 e 2-3 lidos foram
de 30o
30’50” e 28o
30’00” respectivamente.
Com base no procedimento de campo descrito acima, responda as seguintes
perguntas:
A ) Qual é a distância horizontal 1-3?

56. 50
B ) Qual é a distância horizontal 2-3?
C ) Qual é a altitude da estaca 2?
D ) Qual é a altitude do ponto inacessível 3?
E ) Faça um esboço da operação descrita.
8 ) Qual a área real de um terreno cujas dimensões representadas em uma
planta planimétrica, escala 1:2.500, são: 10cm de frente e 30cm de fundo.
9 ) Qual a área, em alqueires paulista, de uma poligonal cujo levantamento
topográfico resultou nas seguintes coordenadas finais para os vértices?
Vértice 1 ( 202 Este; 300 Norte );
Vértice 2 ( 250 Este; 315 Norte );
Vértice 3 ( 240 Este; 290 Norte );
Vértice 4 ( 210 Este; 250 Norte ).
10) Os vértices 1 e 2 de uma poligonal apresentam as seguintes
coordenadas:
Vértice 1: 500m Este; 500m Norte;
Vértice 2: 480m Este; 540m Norte.
Com base nestes dados, qual é o R1,2, o Az1,2, o R2,1,Az2,1 e a distância 1-2?
2.7.5 Método das Coordenadas Retangulares
A) Aplicação: Pela facilidade e rapidez das operações, este método é
especialmente indicado para levantamento de detalhes que apresentam
configuração curvilínea (Rios, divisas de propriedades).
Neste método, a posição do ponto topográfico de interesse é
definida pela medição de suas coordenadas retangulares (X,Y). Um dos
lados da poligonal de apoio servirá como eixo de referência para medição
das abcissas e ordenadas.

57. 51
Definindo o eixo de referência, sobre ele serão marcadas as abcissas
(X) dos pontos de interesse; perpendicularmente, anotam-se as ordenadas
(Y).
P2 P4
P1 P3
X1
X2
X3
X4
X e Y são medidos com trena ou calculado comTeodolito Taqueométrico.
B) Precisão: Este método não conduz a resultados precisos, devido ao fato
de se utilizar somente de medidas lineares. Entretanto, pela
facilidade de operação e rápida execução, é recomendado o seu
uso em levantamento de detalhes.
2.8 Levantamento dos Detalhes
2.8.1 Definição de Detalhes
Denomina-se detalhes os elementos do terreno que, por sua
importância, característica ou posição relativa, devem compor a planta
topográfica.
Os detalhes podem ser rios, lagos e praias; florestas e lavouras; obras
de engenharia; acidentes naturais, relevos e etc.
Y1 Y2 Y3 Y4

58. 52
2.8.2 Métodos de Levantamento de Detalhes
No geral, todos os métodos de levantamento topográfico estudados
podem ser utilizados na determinação e representação dos detalhes,
contudo, pelas características particulares de cada um, em certas situações
uns são mais indicados que os outros. Há situações em que se faz
necessário o uso de métodos combinados para determinação dos detalhes.
É importante frisar que, na prática, muitas vezes o bom senso do
profissional definirá qual o melhor procedimento a ser adotado.
No escritório calculam-se as coordenadas dos pontos empregando-se
técnicas de desenho, confecciona-se o desenho final de acordo com as
informações contidas no croqui.
Em geral, os detalhes são representados por meio de símbolos; estes
símbolos, denominados de “convenções topográficas”, destinam-se a
reproduzir fielmente a natureza dos objetos a representar.
A convenção topográfica é um recurso utilizado para representar no
desenho detalhes que, se postos na escala do referido desenho seriam
imperceptíveis a vista humana.
A NBR 13133/94 apresenta relação de convenções topográficas.

59. 53
( )
( )ME
d
S
yyyyyy
d
S
b
b
.2
2
2222
2
654321
+=
+++++=
2.9 ÁREAS EXTRAPOLIGONAIS
2.9.1 Cálculo da área Extrapoligonal
A Método analítico
B E
C D
F
A
y1 y2 y3 y4 y5 y6
d d d d d
d= todas as partes devem ser iguais.
A.1 Fórmula dos trapézios ou de BEZOUT

60. 54
( )PIE
d
Ss 42
3
++=





 −
+=
4
'
2.
EE
PdS p
Onde E é o somatório dos y extremos
Onde M é o somatório dos y do meio.
A.2 Fórmula de SIMPSON
Onde E é o somatório dos y extremos;
Onde I é o somatório dos y ímpares;
Onde P é o somatório dos y Pares;
A.3 Fórmula de PONCELET
Onde E é o somatório dos y extremos;
Onde E’ é o somatório dos y adjacentes aos extremos (2° e Penúltimo);
Onde P é o somatório dos y Pares;
EXERCÍCIO
20 20 20 20 20 20
Y=1,8
Y2=3,5
Y3=4,7
Y4=5,5
Y5=5,8
Y6=5,4
Y7=3,8

61. 55
2
( )
( ) 2
5549,24.26,5
2
20
.2
2
mS
ME
d
S
b
b
=+=
+=
( )
( ) 2
2772,5616,57216,5666,6
42
3
mS
PIE
d
S
s
s
=++=
++=
2
5,559
4
9,86,5
8,2820
4
'
2
mS
EE
PdS
p
p
=




 −
+=





 −
+=
Calcular a área
Obs.: Todas as medidas estão em metro
EXERCÍCIO
1 ) As sapatas de fundação de uma edificação estão dispostas formando um
triângulo. O azimute do alinhamento formado pelas sapatas 1 ( S1 ) e 3 ( S3
) é de 89o
20’ 37” ( AzS1-S3 ); o do alinhamento formado pelas sapatas S1 e
2 ( S2 ) é de 35o
15’ 30” ( AzS1-S2 ) e o do alinhamento formado pelas
sapatas S2 e S3 é de 130o
20’ 40” ( AzS2-S3 ). As coordenadas da sapata S1
são 100m Norte, 100m Este, e, da S3, 100,945m Norte, 182,494m Este.
Com base neste enunciado, responda as seguintes questões:
a ) Quais são as coordenadas da sapata S2?
1
3

62. 56
b ) Qual é a área do triângulo definido pelas sapatas S1, S2 e S3?
c ) Qual é o afastamento entre os eixos Norte-Sul das Sapatas S1 e S2, e
das Sapatas S2 e S3?
d ) Qual é o afastamento entre os eixos Este-Oeste das Sapatas S1 e S2, e
das Sapatas S1 e S3?

63. 57
3 ALTIMETRIA
A altimetria é a parte da topografia que tem por objetivo a
determinação das alturas dos pontos do terreno, definidos pela planimetria,
em relação a uma superfície de referência e cuja finalidade é a
representação do relevo através de curvas de nível. Dependendo da
superfície de referência adotada, temos as cotas e as altitudes.
3.1 COTAS E ALTITUDES
As cotas correspondem a menor distância entre pontos da Superfície
Topográfica, quando representada numa Carta ou Planta Topográfica de
uma região, e uma superfície de referência arbitrária. Por outro lado, as
altitudes correspondem a menor distância entre pontos da Superfície
Topográfia e a superfície de nível médio dos mares, ou do Geóide, tomada
como referência. Chamamos de Afastamento a menor distância em relação
à superfície do Elipsóide de Referência. As cotas negativas ou de
profundidade são denominadas cotas batimétricas.
Normalmente chamamos de Superfície Topográfica à superfície do
relevo continental, e superfície batimétrica ao assoalho submarino.
Entretanto, a Superfície Topográfica compreende a superfície sólida da
Terra, incluindo o relevo continental e o assoalho submarino.
3.2 DIFERENÇA DE NÍVEL
As diferenças existentes entre as cotas ou altitudes dos pontos do
terreno são designadas de diferença de nível ( Figuras 01 e 02 ). Podemos

64. 58
também dizer que a diferença de nível entre dois pontos do terreno
corresponde à distância vertical entre os planos que contém estes pontos.
O levantamento altimétrico de um ponto consiste na determinação da
diferença de nível entre esse ponto e outro de cota ou altitude conhecida e,
por conseguinte, no conhecimento da cota ou altitude daquele ponto.
3.3 REFERÊNCIA DE NÍVEL
Chama-se referência de nível ou simplesmente RN a um ponto de
cota ou altitude conhecida. Estes RN são de extrema importância nos
trabalhos topográficos. São encontrados nos terminais de estradas de ferro.
Além destes pontos, existem outros distribuídos pelo País, levantados pelo
Departamento Nacional da Produção Mineral ( DNPM ) ou pelas empresas
de aeronáutica civil. Normalmente estes RNs são pontos notáveis, onde são
fixados marcos de cimento, locados nas principais cartas do País.
3.4 NIVELAMENTO
O nivelamento consiste no conjunto de operações topográficas
realizadas com o objetivo de determinar as diferenças de nível entre os

65. 59
pontos do terreno. Qualquer trabalho de nivelamento de grande precisão
deve sempre ser iniciado tendo como base uma referência de nível ( RN ).
3.5 TIPOS DE NIVELAMENTO
Em decorrência da natureza e do processo de medidas usadas na
determinação das cotas ou altitudes, os nivelamentos são classificados, na
ordem de precisão crescente, em: barométrico, trigonométrico e
geométrico.
3.5.1 NIVELAMENTO BAROMÉTRICO
Consiste na obtenção da diferença de nível em função da pressão
atmosférica obtida em dois pontos diferentes. Desta forma a altitude de um
ponto é determinada mediante a medida da pressão atmosférica em um
ponto de altitude conhecida e no outro cuja altitude desejamos saber.
O nivelamento barométrico é de grande emprego no apoio altimétrico para
a aerotriangulação tendo como objetivo a confecção de cartas em pequena e
média escala. Na sua faixa de emprego apresenta grandes vantagens em
relação aos outros métodos pelo baixo custo operacional, pois é de
execução rápida, utiliza equipamento portátil e pequeno efetivo das equipes
de trabalho.
Os altímetros utilizados para obtenção das altitudes a partir da
pressão atmosférica, são semelhantes aos barômetros aneróides. Consistem
em uma cápsula metálica com vácuo no seu interior. As variações de
pressão atmosférica produzem deformações na cápsula, provocando
deflexões em um ponteiro que mede a pressão atmosférica, a qual é

66. 60
traduzida em altitudes através de dispositivos mecânicos relacionados a
uma escala de leitura, em metros ou pés ( escala orométrica ).
Figura 03: Esquema de um barômetro aneróide ( Manual TécnicoT34-604 ).
3.5.2 NIVELAMENTO TRIGONOMÉTRICO
O nivelamento trigonométrico é efetuado com a utilização do
teodolito, cujos dados angulares de campo são tratados segundo as relações
trigonométricas em um triângulo. No nivelamento trigonométrico opera-se,
em geral, com visadas inclinadas. Assim, a diferença de nível entre dois
pontos é determinada por cálculo trigonométrico a partir do conhecimento
da distância horizontal entre os dois pontos, e o ângulo vertical fornecido
pelo teodolito.
Na Figura 04 γ1 e γ2 representam ângulos verticais ( zenitais ); AA a
altura do aparelho medida do eixo de rotação do telescópio até o nível do
terreno indicado por um piquete; L1 a leitura de estádia corresponde ao
ângulo γ1; L2 a leitura de estádia correspondente ao ângulo γ2; ∆L a
diferença das leituras L2 e L1; dH a distância horizontal entre os pontos 1 e
2; ∆ a distância vertical do centro de telescópio até a leitura L1 sobre a mira.
Trigonometricamente a diferença de nível entre os pontos 1 (onde está

67. 61
estacionado o teodolito) e 2 (onde coloca-se a mira estadimétrica), ∆H, será
determinada através das seguintes expressões:
∆H = ∆ + AA – L1, onde ∆ = dH.Cotgγ1, o que nos dá a seguinte expressão
para o cálculo do desnível entre os pontos 1 e 2:
∆H = dH.Cotgγ1 + AA – L1
Figura 04: Nivelamento trigonométrico
Observe que neste caso é necessário conhecer a distância horizontal
dH entre os dois pontos cujo desnível queremos determinar. Entretanto, a
partir da mesma figura, podemos obter a expressão que possibilita o cálculo
do desnível ∆H sem necessidade de sabermos a distância entre os dois
pontos, que é a seguinte:
∆ = ∆L.cotgγ1 / cotgγ2 - cotgγ1, que substituindo na expressão de ∆H nos dá
o seguinte resultado:
∆H = ∆L.cotgγ1 / cotgγ2 - cotgγ1 + AA – L1

68. 62
A mesma equação pode ser obtida substituindo o valor de dH, do ítem
2.6.3, na equação anterior que fornece o valor de ∆H em função de dH.
3.5.3 NIVELAMENTO GEOMÉTRICO
O nivelamento geométrico é comumente empregado nos trabalhos de
topografia, como nivelamento de estradas, construções em geral,
loteamentos, etc. É um nivelamento de boa precisão quando
cuidadosamente aplicado.
3.5.3.1 INSTRUMENTAL UTILIZADO
Para execução de um nivelamento geométrico, o instrumental a ser
empregado necessita estabelecer uma linha de visada horizontal e permitir
a medida de distâncias verticais. Tais instrumentos são os níveis e as miras.
A NÍVEIS
São instrumentos óticos especialmente construídos e consistem de
uma luneta conjugada a níveis de boa sensibilidade, de modo a assegurar
que, estando a luneta estacionada sobre um ponto, possamos orientar com
precisão o seu eixo vertical segundo a vertical do lugar e que ela, ao girar
em torno desse eixo, descreva um plano rigorosamente normal a ele
próprio. Os níveis definem físicamente um plano horizontal ou uma linha
horizontal.
Os níveis podem ser classificados, segundo o órgão visor que são
dotados, em: níveis de luneta, níveis de visor de pínulas e níveis sem órgão
visor. Os nivelamentos mais rigorosos são efetuados com os níveis de

69. 63
luneta, sendo esta semelhante à luneta de um teodolito, apresentando
inclusíve os fios estadimétricos. O único movimento possível das lunetas
dos níveis é em torno de um eixo vertical. Ela é montada sobre uma base
dotada de três parafusos calantes, que permitem o nivelamento do
instrumento, quando instalado sobre o tripé.
As leituras, nos níveis, são sempre feitas em relação ao fio médio.
Quando perfeitamente nivelado, o eixo ótico ou eixo de colimação do
aparelho descreve sempre um plano horizontal.
B MIRAS
As miras são réguas de madeira usadas no nivelamento para determinação
de distâncias verticais. Existem vários tipos de miras: miras simples ou de
alvo, miras falantes e miras de nível. As mais utilizadas nos trabalhos de
topografia são as miras falantes, que são réguas de madeira ou alumínio
com extensão de 3, 4 ou 5 metros, porém, em geral, de 4 metros. Elas
possuem extremidades protegidas por uma peça de aço, tendo uma das
faces graduadas. Os fabricantes de instrumentos topográficos apresentam
miras com vários tipos de graduação.
3.5.3.2 PRINCÍPIO DO NIVELAMENTO GEOMÉTRICO
Consideremos dois pontos A e B da superfície terrestre ( Figura 04 ).
Seja HH o traço de um plano horizontal qualquer, adotado como referência.
Suponhamos instalado num ponto qualquer entre A e B um nível de luneta,
e nos pontos A e B uma mira posta verticalmente, onde se faz as leituras lA
e lB.
Podemos expressar a diferença de nível, DN, entre A e B por:

70. 64
DN = lA – lB ( 1 )
Podemos ainda escrever que:
CB = CA + DN ( 2 ), ou
CB = CA + ( lA – lB ) ( 3 )
A expressão ( 3 ) nos permite definir que o nivelamento geométrico é
a operação que tem por finalidade determinar a cota de um ponto B da
superfície terrestre, sendo conhecida a cota de um ponto A e as leituras
feitas numa mira instalada em A e B.
Quando não se dispõe de um RN, a cota do ponto A pode ser
arbitrada, já que podemos escolher livremente o plano HH.
Figura 04: Princípio do nivelamento geométrico
3.5.3.3 TIPOS DE NIVELAMENTO GEOMÉTRICO
O nivelamento geométrico pode ser simples ou composto:
A. NIVELAMENTO GEOMÉTRICO SIMPLES
O nivelamento geométrico é simples quando é possível visar de uma
única estação de nível a mira colocada em todos os pontos do terreno a
nivelar.

71. 65
Tomemos como exemplo os pontos A, B e C cujos perfís dos
alinhamentos AB e BC estão representados na Figura 05.
Figura 05: Nivelamento geométrico simples
Instala-se o nível em uma posição qualquer N, com a condição de ser
possível visar a mira M colocada na vertical e sucessivamente nos pontos
A, B e C. A primeira visada, feita no ponto A, início do nivelamento, é
chamada “visada a ré” (VR) e as seguintes “visadas a vante” (VV ), que
podem ser “vante de mudança” ( VV) ou “vante intermediária” (VI ).
Conhecida a cota de A, seja por se tratar de um ponto nivelado
anteriormente ou por arbitramento, chama-se “altura do instrumento” (AI )
a soma da cota deste ponto com a visada a ré feita em A ( VRA ), isto é:
AI = CA + VRA
Conhecida a visada feita em B ( VIB ), a cota do ponto B será
calculada através da expressão:
CB = AI – VIB e, por extensão, conhecida a visada em C ( VVC ), a cota do
ponto C será:
CC = AI - VVC

72. 66
B. NIVELAMENTO GEOMÉTRICO COMPOSTO
O nivelamento geométrico composto consiste em uma série de
nivelamentos simples, articulados cada um com o anterior. Este tipo de
nivelamento é realizado sempre que o relevo for acidentado, isto é,
apresentar desníveis acentuados. Nesta situação a diferença de nível entre
dois pontos poderá ultrapassar a altura da mira, obrigando o deslocamento
do instrumento para um ponto que permita a sua visão. Por outro lado, a
necessidade de deslocar o instrumento também se faz necessária quando as
distâncias ultrapassarem o limite de alcance da luneta, o qual está limitado
a 100 metros. Além desta distância as leituras poderão estar sujeitas a erros
inadmissíveis.
As posições dos pontos a nivelar são determinadas anteriormente por
um levantamento planimétrico, e devem definir com propriedade o perfil
do alinhamento entre eles, isto é, necessitam estar situados nos pontos onde
há mudança de inclinação do terreno.
Para execução de um nivelamento geométrico composto, a escolha
do ponto de localização do nível é feita de modo que:
a ) Haja condição de visar o maior número possível de pontos, respeitando
o limite de 100 metros para a distância de visada;
b ) Que a mira situada no último ponto nivelado do trecho anterior, possa
ser visada.
A Figura 06 mostra o exemplo de uma situação de campo para o
nivelamento entre os pontos A e F.

73. 67
Figura 06: Nivelamento geométrico composto
Com o nível em N1 visa-se a mira em A e B e faz-se as leituras VRA e
VVB, respectivamente, que correspondem às visadas a ré em A e vante em
B. Em seguida instala-se o nível em N2, já que de N1 não será possível visar
a mira em C. Em seguida efetua-se a leitura no último ponto, B, do
nivelamento anterior, o que caracteriza a visada a ré VRB, e sucessivamente
são efetuadas as leituras VIC em C e VVD em D. Repete-se a operação com o
nível instalado em N3 e efetua-se as visadas VRD, VIE, e VVF.
Conhecida ou arbitrada a cota CA do ponto inicial A, calcula-se as
cotas dos demais pontos, através das seguintes operações aritméticas:
AI1 = CA + VRA AI2 = CB + VRB AI3 = CD + VRD
CB = AI1 - VVB CC = AI2 - VIC CE = AI3 - VIE
CD = AI2 - VVD CF = AI3 - VVF
O pontos “B” e “D” são pontos importantes no nivelamento
geométrico composto porque é mediante estes que se articulam os trechos
nivelados. Assim, estes pontos, receberão duas visadas, sendo a primeira
para determinação da sua cota e denominada de “visada vante de mudança”

74. 68
uma vez que a partir dela o aparelho muda de estação, e a segunda para
determinação da nova altura do instrumento, sendo denominada de “visada
a ré”.
3.5.4 ERRO DE NIVELAMENTO
O nivelamento pode ser aberto ou fechado. É dito aberto quando não
há retorno ao ponto inicial, ou quando não termina em um ponto de cota ou
altitude conhecida. É fechado quando retorna ao ponto de partida, ou
quando termina em um ponto de cota ou altitude conhecida.
Nos nivelamentos abertos a verificação do erro cometido é feita retornando
ao ponto de partida após a determinação da cota ou altitude do último
ponto, fazendo-se o nivelamento em sentido contrário. Esta operação é
denominada de Contranivelamento.
3.5.5 PLANILHA DE NIVELAMENTO GEOMÉTRICO
As grandezas medidas no nivelamento geométrico são registradas em
uma planilha denominada “planilha de nivelamento geométrico”,
constituída das seguintes colunas: pontos nivelados ( estacas ), visadas a ré,
altura do instrumento, visadas a vante ( intermediária e de mudança ),
distâncias, cotas ou altitudes e observações, conforme planilha a seguir:

75. 69
PLANILHA DE NIVELAMENTO GEOMÉTRICO
Estaca Visada
a ré
Altura do
Instrumento
VisadaVante
intermediária
VisadaVante
de Mudança
Distância
entre estaca
Cotas ou
Altitudes
Observações
01 82,402m RN
1,230m 83,632m 35,50m
02 0,802m 25,00m 82,830m
03 2,542m 81,090m
1,980m 83,070m 30,00m
04 3,540m 35,00m 79,530m
05 2,150m 20,00m 80,920m
06 0,750m 82,320m
Observa-se que na planilha de exemplo o instrumento ocupou duas
posições: a primeira quando fez a visada a ré na estaca 01 de 1,230m para
determinar a altura do instrumento de 83,632m; a segunda quando fez a
visada a ré na estaca 03 de 1,980m para determinar a altura do instrumento
de 83,070m, após ter efetuado a visada vante de mudança também na
estaca 3. Por conseguinte, verifica-se que uma estaca de mudança recebe
duas visadas, sendo uma para determinar a sua cota ( visada vante de
mudança ) e a outra para determinar a nova altura do instrumento ( visada a
ré ). Assim, a denominação visada a ré caracteriza aquela visada que
sempre é feita para um ponto de cota conhecida com a finalidade de
determinar a nova altura.

76. 70
3.5.6 VERIFICAÇÃO DO CÁLCULO DA PLANILHA
Considerando apenas as estacas de articulação entre os diversos
trechos de nivelamento simples, já que é através destes pontos que o
cálculo das cotas se propaga, temos de acordo com a Figura:
AI1 = CA + VRA VVB = VMB
CB = AI1 - VVB VVD = VMD
AI2 = CB + VRB VVF = VMF
CD = AI2 - VVD
AI3 = CD + VRD
CF = AI3 - VVF
Somando membro a membro, temos:
CF = CA + VRA – VMB + VRB - VMD + VRD - VMF
CF = CA + ΣVR - ΣVVM, ou, CF – CA = ΣVR - ΣVVM, onde:
CF = cota final
CA = cota inicial
ΣVR = soma das visadas a ré
ΣVVM = soma das visadas vante de mudança, ou seja:
A diferença entre as cotas extremas de um nivelamento é igual a soma das
visadas a ré menos a soma das visadas vante de mudança.
Para os nivelamentos fechados, temos:
CF = CA ⇒ CF – CA = ΣVR - ΣVVM ⇒ ΣVR - ΣVVM = 0
Entretanto, na prática isto não ocorre e quando fechamos o
nivelamento verifica-se que:

77. 71
ΣVR - ΣVVM = εa, isto é, a soma das visadas a ré subtraída da soma das
visadas vante de mudança é diferente de zero, o que indica o erro absoluto
cometido, correspondente ao somatório dos erros cometidos nas leituras
feitas na mira. O erro relativo, εr, será:
εr =
a
p
ε
2
1
onde 2p é o perímetro da poligonal ou a extensão do trecho
nivelado quando se tratar do nivelamento de um alinhamento.
O erro será admissível se estiver dentro dos limites de tolerância
estabelecidos, sendo distribuído para as cotas dos diversos pontos
nivelados. É comum considerar os seguintes limites:
a ) Para nivelamentos de alta precisão: εr ≤ 1,5mm/Km
b ) Para nivelamentos de precisão: εr ≤ 3mm/Km
c ) Para nivelamentos de 2a
ordem: εr ≤ 10mm/Km
d ) Para nivelamentos de 3a
ordem: εr ≤ 30mm/Km
A precisão de um nivelamento depende da precisão do nível utilizado
e da extensão da poligonal ou do trecho nivelado. Assim, temos para o erro
admissível em um nivelamento a seguinte expressão:
εad = e u , onde:
e = precisão do nível em milímetro;
u = perímetro da poligonal ou do trecho nivelado
εad = erro admissível
Exemplo:
e = 2,5mm/Km
u = 2,0Km
εad = e u = 2,5mm 2 = 3,5mm
O erro de nivelamento deverá ser distribuído em partes iguais nos
pontos de estacionamento do nível.

78. 72
AIn
ad
n
.
ε
=∆ , onde:
∆n = parcelas a serem distribuídas
εad = erro admissível
n.AI = número de pontos de estacionamento do nível.
Tomemos como exemplo a planilha abaixo referente a um
nivelamento fechado, tendo como ponto de partida a estaca 01 e término na
mesma estaca:
PLANILHA DE NIVELAMENTO GEOMÉTRICO
Estaca Visada
à ré
Alturado
instrumento
Visada Vante
intermediária
Visada Vante de
mudança
Distância
entre estacas
Cotas ou
altitudes
Observações
01 50,000m RN
1,650m 51,650m 10,00m
02 2,500m 10,00m 49,150m
03 1,400m 50,250m
1,200m 51,450m 15,00m
04 1,500m 20,00m 49,950m
05 1,650m 49,800m
0,780m 50,580m 25,00m
06 1,200m 30,00m 49,380m
07 1,350m 15,00m 49,230m
01 0,568m 50,012m
Pela condição do nivelamento fechado, devemos ter:
CF = CI, isto é, a cota final (CF) deve ser igual a cota inicial (CI).
Entretanto, observa-se que a diferença CF-CI = 50,012m-50,000m =
12mm, ou seja, houve um erro de 12 milímetros no nivelamento.
Admitindo-se que se trata de um erro admissível, a parcelas a serem
distribuídas serão:

79. 73
AIn
ad
n
.
ε
=∆ =
3
12mm
= 4mm
Estes 4mm serão distribuídos acumulativamente nos pontos de
estacionamento do aparelho, ou uniformemente nas visadas à ré. O
primeiro será subtraído de 4mm, pois o erro foi para maior; o segundo de
8mm e o terceiro de 12mm, ficando a tabela corrigida com os seguintes
valores para as cotas e alturas do instrumento:
PLANILHA DE NIVELAMENTO GEOMÉTRICO CORRIGIDA
Estaca Visada
à ré
Alturado
instrumento
Visada Vante
intermediária
Visada Vante de
mudança
Distância
entre estacas
Cotas ou
altitudes
Observações
01 50,000m RN
1,646m 51,646m 10,00m
02 2,500m 10,00m 49,146m
03 1,400m 50,246m
1,196m 51,442m 15,00m
04 1,500m 20,00m 49,942m
05 1,650m 49,792m
0,776m 50,568m 25,00m
06 1,200m 30,00m 49,368m
07 1,350m 15,00m 49,218m
01 0,568m 50,000m
Observa-se que na primeira altura do instrumento foram retirados
4mm, na segunda 8mm e na terceira 12mm, resultando a cota da estaca 01,
no final, igual à cota inicial (RN).
3.6 CURVAS DE NÍVEL
As curvas de nível, também conhecidas como curvas horizontais ou
hipsométricas, foram utilizadas pela primeira vez em 1730 pelo engenheiro

80. 74
Cruquius no traçado das curvas dos leitos dos rios ( Espartel, 1978 ). São as
linhas que ligam os pontos, na superfície topográfica, que possuem a
mesma cota ou altitude. A sua construção é feita segundo intervalos que
definem a diferença de cota ou altitude entre duas curvas consecutivas.
Estes intervalos dependem da escala da planta e da declividade do terreno.
Assim, por exemplo, um terreno com declividade de 40%, apresenta uma
queda de nível de 1 metro em cada 2,50 metros de distância horizontal. Se
formos representar esta declividade em curvas de nível equidistantes de 1
metro em uma escala de 1:8.000, o afastamento entre elas será:
md
D
d
E 0003125,0
000.8
50,2
000.8
1
==⇒== seja, o afastamento será de
praticamente 0,3mm, ficando as referidas curvas quase que remontadas.
Para plantas em escala maiores que 1:1.000, estes intervalos podem
ser menor que 1 metro; nas escalas até 1:1.000, 1 metro, e 2 metros até
1:2.000. As curvas de nível resultam da projeção ortogonal das interseções
de planos horizontais equidistantes, paralelos entre si e a um plano
horizontal de referência, que é o Plano-Topográfico de projeção
( Figura 07 ). Este plano de projeção se confunde com a superfície de nível
médio do mar ( Geóide ) num trecho relativamente limitado da superfície
da Terra. As curvas de nível projetadas sobre o Plano-Topográfico,
conservam sua forma e suas dimensões nesse plano. A Figura 08 mostra
uma planta topográfica planialtimétrica com a redução de suas dimensões
de acordo com a escala adotada para o desenho.

81. 75
Figura 07: Relevo e sua representação em curva de nível
Figura 08: Planta Topográfica planialtimétrica em uma escala E
3.6.1 TRAÇADO DAS CURVAS DE NÍVEL
Para traçarmos as curvas de nível há necessidade de locarmos um
número suficiente de pontos sobre a superfície topográfica para, em

82. 76
seguida, mediante nivelamento, determinarmos as suas cotas ou altitudes.
A locação dos pontos a serem nivelados pode ser feita de três formas:
a ) Estabelecimento de uma malha quadriculada;
b ) Determinação taqueométrica por irradiação;
c ) Perfis transversais.
O estabelecimento de uma malha quadriculada resulta em um
trabalho de boa precisão, porém é muito demorado e dispendioso não sendo
conveniente a sua aplicação em áreas muito grandes. É recomendada a sua
utilização em trabalhos de terraplanagem, uma vez que envolve grandes
somas de dinheiro, o que justifica a sua aplicação.
O método consiste em piquetear o terreno segundo uma malha
quadrada e, em seguida, efetuar o nivelamento geométrico dos piquetes.
A determinação taqueométrica das cotas é feita por irradiação a partir dos
vértices da poligonal de apoio, escolhendo-se pontos aleatoriamente, porém
representativos das variações do relevo. Para isto concorre a experiência do
topógrafo. A determinação taqueométrica por irradiação é muito utilizada
para áreas extensas como as utilizadas para implantação de loteamentos.
O método dos perfis transversais é utilizado para terrenos de pequena
largura e muito compridos, o que facilita o traçado de perfis transversais
equidistantes ou não. Estas características o recomendam para o
nivelamento de obras civis lineares como rodovias, ferrovias, adutoras,
linhas de transmissão e oleodutos. Em rodovias, as seções transversais são
niveladas taqueométricamente distando cada uma da outra, 20 metros.
Efetuado o nivelamento e locados os pontos em planta, procede-se à
operação seguinte que é a interpolação. A interpolação consiste em estimar

83. 77
valores de cotas ou altitudes de pontos situados entre outros cujas cotas ou
altitudes foram determinadas no campo.
Para que não se faça interpolações desnecessárias e errôneas, as
seguintes observações devem ser feitas:
a ) Proximidade imediata dos pontos de interpolação;
b ) As direções de interpolação não devem se cruzar;
c ) As direções de interpolação não devem passar próximas a pontos de
cota conhecida.
3.6.2 INTERPOLAÇÃO
A interpolação pode ser feita graficamente ou analiticamente. No
método gráfico, a rotina do processo é a seguinte:
a ) Os pontos do terreno locados panimetricamente e cujas cotas foram
determinadas pelos métodos já descritos, são lançados no desenho. Na
parte “a” da Figura 09 vemos os quatros pontos de cotas 101,5, 102,8,
108,4 e 103,5. Estas cotas em geral resultam fracionárias;
b ) No passo seguinte ligam-se os pontos de cotas mais baixas ao ponto
mais próximo de cota mais elevada, 108,4, conforme mostrado na parte “b”
da Figura 09 e, em seguida, determina-se em cada um dos segmentos de
reta os pontos de cota inteira por interpolação entre as cotas extremas;
c ) Por fim, ligam-se por linhas traçadas manualmente os pontos de cotas
inteiras iguais, as quais constituem as curvas de nível conforme mostrado
na parte “c”da Figura 09.

84. 78
Figura 09: Traçado das curvas de nível ( Mesquita, 1969 ).
3.6.3 DETERMINAÇÃO DOS PONTOS DE COTA INTEIRA
A graduação de uma reta cujos pontos extremos são de cota
conhecida, é feita adotando-se o seguinte procedimento:
Na Figura 10 temos os pontos A e B cujas cotas são 102,6 e 108,2m
respectivamente. Traça-se um segmento de reta auxiliar AM indefinido
formando um ângulo aproximado de 45o
com o segmento AB. Em seguida
procede-se à graduação da reta auxiliar segundo a escala do desenho,
obtendo-se os pontos 103, 104, 105, 106, 107, 108 e o ponto B’ 108,2 sobre
o segmento auxiliar. Na etapa seguinte ligam-se os pontos de mesma cota (
B’e B ), traçando-se o segmento B’B. Paralelamente ao segmento B’B,

85. 79
traçam-se segmentos de reta que interceptarão o segmento AB que une os
dois pontos de cota conhecida ( 102,6 e 108,2 ). Com este procedimento
determinam-se sobre AB os pontos de cotas 103, 104, 105, 106, 107 e
108.O processo baseia-se no Teorema de Thales de divisão de um
segmento em partes proporcionais.
Figura 10: Graduação de um segmento de reta a partir de um auxiliar
( Mesquita, 1969 ).
Outro método de interpolação gráfica também pode ser utilizado.
Na Figura 11 os pontos A e C são de cotas conhecidas. Traçam-se
por A e C duas paralelas não necessariamente perpendiculares ao segmento
de reta AC. Marcam-se as distâncias 0,4 e 0,7, que na escala do desenho
correspondem às distâncias necessárias para se chegar de 15,6 a 16 e de
16,7 a 16. Determinam-se, assim, os pontos F e M que unidos pelo

86. 80
segmento de reta FM intercepta o segmento AC no ponto N que possui a
cota 16 procurada entre A e C.
Figura 11: Interpolação gráfica e analítica
A interpolação analítica é feita por semelhança de triângulos. Na
Figura 11 os triângulos FAN e MCN são semelhantes. Portanto:
mxxxxx
x
x
x
x
FA
CM
27,7
1,1
8
84,07,04,087,0
20
4,0
7,020
==⇒=+⇒−=⇒
−
=⇒
−
=
Como x é igual à distância AN do ponto A até o ponto N no segmento de
reta AC, marca-se então, na escala do desenho, a distância de 7,27m
localizando-se o ponto N.

87. 81
EXERCÍCIOS
1 ) Completar a planilha de nivelamento geométrico abaixo com os valores que faltam,
fazer a prova de cálculo e o esquema do procedimento de campo adotado.
Estaca Visada a ré Altura do
instrumento
Visada Vante
Intermediária
Visada Vante
de Mudança
Cota
RN-20 52,423
52,562
2 50,140
3 3,520
0,402
4 47,919
5
1,100
6 1,960 44,768
7 2,713
44,535
8 41,313
9 40,715
10
2,350
11 3,720 42,113
12 3,583
2 ) Admitindo a distância de 20 metros entre as estacas, desenhar o perfil topográfico
correspondente ao trecho nivelado.
3 ) O esquema abaixo é de um nivelamento geométrico realizado na encosta de uma
elevação. A linha pontilhada representa, em planta, os obstáculos da encosta que
obrigaram o deslocamento sucessivo do aparelho. Os algarismos romanos indicam as
posições ocupadas pelo aparelho, e os arábicos até 14 as estacas de nivelamento. As
cotas dos pontos e alturas do instrumento fornecidas, estão ao lado do número
correspondente. Os números ao longo das setas indicam as leituras de mira. Pede-se:
organizar a planilha de cálculo, calcular o erro de nivelamento e fazer a distribuição
deste erro em cada uma das estacas.

88. 82
4 ) Baseando-se no esquema de procedimento de campo abaixo, adotado
para nivelamento do perfil da estaca 01 para a estaca 08, montar a planilha
de nivelamento correspondente com todos os valores dados, calculados e
fazer a prova de cálculo.
5 ) Admitindo a distância de 30 metros entre as estacas 1-2, 3-4, 5-6 e 20
metros entre as demais estacas, desenhar o perfil topográfico
correspondente.
6 ) O levantamento topográfico de um terreno apresentou os seguintes
resultados:
a ) do vértice 1 para o vértice 2, Az1,2 = 204o
12’30”; dH1,2 = 44,395m
b ) do vértice 2 para o vértice 3, Az2,3 = 277o
57’30”; dH2,3 = 41,728m
c ) do vértice 3 para o vértice 4, Az3,4 = 20o
54’30”; dH3,4 = 36,012m
d ) do vértice 4 para o vértice 1, a distância determinada foi de 46,575
metros.
Com base nestes resultados, determinar o azimute do vértice 4 para o
vértice 1, Az4,1.
7) Em um determinado levantamento topográfico, a altura do aparelho na
estaca 1 era de 1,56 metros, e os ângulos zenitais e respectivas leituras de
mira posicionada na estaca 2 foram:
γ1 = 91o
55’40”; l1 = 2,100m
γ2 = 91o
01’30”; l2 = 2,800m
Admitindo como sendo 52,250m a cota da estaca 1, qual é a cota da estaca
2 e qual o comprimento do lado 1-2?

89. 83
3.7 ELABORAÇÃO DE UM PERFIL TOPOGRÁFICO A PARTIR
DA PLANTA TOPOGRÁFICA COM CURVAS DE NÍVEL.
Na Figura 12 temos as curvas de nível representativas do relevo de
uma determinada área, equidistantes de 1m. Interessa-nos elaborar o perfil
topográfico definido pelo segmento A-B. A extremidade A deste segmento
intercepta a curva de nível de cota 91m no ponto “a” e a extremidade B a
curva de nível de cota 97m no ponto “g”. No prolongamento de A para B
são interceptadas as curvas de nível 92, 93, 94, 95 e 96m, nos pontos “b”,
“c”, “d”, “e” e “f” respectivamente. O procedimento para elaboração do
perfil topográfico é o seguinte:
a ) Traçamos, na porção superior ou inferior como mostrado na Figura 12,
o segmento A’- B’ paralelo a A-B;
b ) Em seguida traçamos paralelas a A’- B’, tantas quantas forem as
diferentes curvas de nível interceptadas pelo segmento A-B. Estas paralelas
deverão estar afastadas de uma distância correspondente à equidistância das
curvas de nível da planta. No nosso exemplo ela é de 1 metro. Por outro
lado, elas também deverão ser cotadas de baixo para cima em ordem
crescente, recebendo a primeira linha a menor cota e, a última, a maior cota
compreendida pelo perfil em questão. No nosso exemplo estas cotas são a
91 e a 97;
c ) No passo seguinte, projetam-se os pontos “a”, “b”, “c”, “d”, “e”, “f “e
“g” sobre o segmento paralelo a A’- B’ de cota correspondente. Assim
obtemos os pontos a’, b’, c’, d’, e’, f’e g’. A união destes pontos fornece o
perfil topográfico definido pelo segmento A-B.
No desenho de um perfil topográfico temos duas escalas a serem
consideradas: a escala horizontal, Eh , e a escala vertical, Ev. Quando
elaboramos o perfil na própria planta, como no exemplo, a escala
horizontal será a da planta. No nosso exemplo da Figura 12 a escala da
planta é 1:200. Nesta escala está representado o segmento A-B e todas as
suas paralelas. Com relação à escala vertical, ela poderá ser alterada, caso
seja interesse realçar as irregularidades do relevo, o que pode ser feita
aumentando-se a escala, resultando em um maior afastamento das paralelas
a A’- B’. Na Figura 12 a escala vertical adotada também foi de 1:200.

90. 84
Figura 12: Elaboração de um perfil topográfico
3.8 DETERMINAÇÃO DA COTA DE UM PONTO SITUADO
ENTRE CURVAS DE NÍVEL
Na figura 13 temos o ponto “d”situado entre as curvas de nível de
cotas 92 e 93 metros. Interessa-nos saber qual é a cota do ponto “d”. O
procedimento é o descrito a seguir:
a ) Traçamos o segmento a-a’contendo o ponto “d”e perpendicular às duas
curvas de nível. Quando não for possível este perpendicularismo
simultâneo, procura-se fazê-lo o mais próximo permitido;
b ) No passo seguinte medimos o comprimento dos segmentos a-a’e a-d,
estabelecendo a seguinte proporção:
da
aa
−
− '
=
cd
aa
−
− "'
No nosso exemplo os valores são os seguintes:
a-a’= 1cm;
a-d = 0,4cm;
a’- a”= 1 metro que é a equidistância entre as curvas de nível;

91. 85
d-c é a incógnita que corresponde ao desnível do ponto “d”em relação ao
ponto “a” conforme mostra o perfil na porção inferior da Figura 13.
Fazendo as substituições na proporção estabelecida, encontramos o
valor 0,4 metro, que resulta então na cota de 92,4 metros para o ponto “d”,
isto é, 92 + 0,4 = 92,4.
Figura 13: Determinação da cota de um ponto situado entre curvas de nível
3.9 ELABORAÇÃO DE UM PERFIL TOPOGRÁFICO A PARTIR
DE PONTOS NIVELADOS.
Tomemos as cotas das estacas niveladas da planilha de nivelamento
geométrico da página 69. A partir desta planilha traçamos o perfil da Figura
14. O procedimento adotado foi o descrito a seguir:
a ) Adotamos um sistema de eixos cartesianos, onde no eixo “x”, conhecido
como eixo das abcissas, lançamos as distâncias entre estacas. De acordo

92. 86
com a planilha tomada como exemplo, temos as estacas 01, 02, 03, 04, 05 e
06. Para simplificar, alteramos as distâncias entre estacas para 10 metros.
Esta distância deverá ser lançada de acordo com a escala horizontal
escolhida. No nosso exemplo da Figura 14 a escala adotada foi 1:500, onde
cada centímetro no desenho representa cinco metros de distância real entre
estacas;
b ) No eixo “y”, conhecido como eixo das ordenadas, lançamos as cotas ou
altitudes das estacas constantes da planilha tomada como exemplo. Estas
cotas ou altitudes também deverão ser lançadas de acordo com a escala
vertical adotada. No exemplo a escala adotada foi 1:50, onde cada
centímetro no desenho representa 0,50 metros de desnível;
c ) No passo seguinte traçamos paralelas ao eixo das cotas passando pelas
diversas estacas (linhas verticais). Em seguida traçamos paralelas ao eixo
das estacas (linhas horizontais) cruzando o eixo das cotas nos pontos onde
elas foram assinaladas. O cruzamento das linhas verticais das estacas com
as linhas horizontais correspondestes às suas cotas, determinam a sua
posição na superfície topográfica. A união destes pontos fornece o perfil
topográfico desejado.

93. 87
Figura 14: Elaboração de perfil topográfico a partir de pontos nivelados
3.10 DETERMINAÇÃO DA DECLIVIDADE ENTRE DOIS
PONTOS
A declividade, em porcentagem, entre dois pontos é determinada
calculando-se a tangente do ângulo que o segmento de reta que une estes
dois pontos forma com a horizontal. Por exemplo, na Figura 14 a
declividade entre as estacas 4 e 6 é calculada achando-se a tangente que o
segmento de reta, que une as duas estacas em questão, forma com a
horizontal e, em seguida, multiplica-se por 100. Desta maneira temos:
Declividade E4-E6 =
20
79,2
x 100% = 13,95%

94. 88
Quando temos o ângulo de inclinação da rampa e pretendemos saber
qual é a sua declividade em porcentagem, basta multiplicar a tangente do
ângulo de inclinação por 100. Se o ângulo de inclinação do segmento que
une dois pontos da superfície topográfica é de 20o
30’40”, então sua
declividade será:
Declividade = tg 20o
30’40” x 100 = 37,41%
A determinação da declividade entre dois pontos é importante no
traçado dos arruamentos dos projetos de loteamentos, pois a Lei no
1208 de
25/03/1975 – Código de Obras, estabelece em seu Art. 272, Inciso V: “as
declividades máximas das vias urbanas serão de 10% e as mínimas de
0,5%. Poder-se-ão admitir declividades até 15% mediante cabal
demonstração de impossibilidade prática de atendimento”. Ainda com
relação à mesma Lei, em seu Art. 275, fica determinado que: “Nos
loteamentos não se admitirão lotes para fins habitacionais ou reservados
para equipamentos comunitários em terrenos de declividade superior a 30%
salvo quando nas faixas ribeirinhas e nas áreas oficialmente declaradas
estâncias hidrominerais”.

95. 89
4 NOÇÕES DE TERRAPLANAGEM
Terraplanagem ou terraplenagem compreende o conjunto de
operações de escavação, transporte, deposição e compactação de terras
necessárias para realização de uma obra. Dependendo dos volumes de corte
e aterro envolvidos, e do tipo de equipamento utilizado temos:
terraplanagem manual, terraplanagem mecanizada e terraplanagem
compensada:
a) Terraplanagem manual: quando utiliza equipamentos manuais e
rudimentares como pá, picareta, enxada e veículos de tração animal
para o transporte do material envolvido;
b) Terraplanagem mecanizada: quando emprega máquinas e veículos
especializados como bowldozers, scrapers, motoniveladora, pá
carregadeira, caminões fora-de-estrada, rôlo pé-de-carneiro, rôlo liso de
aço, rôlo vibratório, rôlo pneumático etc...
c) Terraplanagem compensada: quando há equivalência entre os volumes
escavados e aterrados, resultando em um mínimo de material para bota-
fora ou empréstimo.
No processo de escavação e aterro de uma obra de terraplanagem,
surgem os TALUDES ARTIFICIAIS, que são as superfícies inclinadas
próximas a obras civís lineares, mineração, etc. Distinguem-se dos taludes
naturais que são as superfícies inclinadas do relevo.
Nos projetos de terraplanagem estes taludes artificiais são especificados
através da inclinação a ser adotada, a qual deverá ser compatível com a
resistência mecânica do material envolvido. Ela é expressa através da
relação entre o desnível de dois pontos situados sobre a superfície do
talude, e a distância horizontal entre eles. Assim, temos taludes 2:1, 1:1,
3:1, 1:2, 1:3 etc (Figura 15).

96. 90
Figura 15: Exemplos de taludes de corte e aterro.
Os pontos P e T são as interseções da superfície de corte ou aterro
com a superfície topográfica. Definem o pé e o topo do talude. A união de
todos os pontos do topo resulta na linha de “off-set”, que servirá de
orientação para o operador de máquinas ao iniciar o corte. Os taludes de
aterro, em geral, são mais abatidos e portanto o numerador é sempre menor
que o denominador na fórmula de especificação (letra c da Figura 15).
O ângulo “α” ( inclinação do talude ) pode ser calculado através do
arctgα. Assim, por exemplo, o ângulo do talude exemplificado na letra “a”
da Figura 15 será:
Arctgα =
1
2
= 63o
26’05”
Taludes com ângulo de inclinação muito acentuado são escavados
em rochas ( Figura 16 ). Assim, por exemplo, temos taludes 4:1, 5:1 etc..,
cujos ângulos de inclinação correspondem a 75o
57’49” e 78o
41’24”
respectivamente. Quando escavados em solo ou rocha alterada, são mais
abatidos, isto é, o seu ângulo de inclinação é menor, resultando em taludes
1:1, 1:0,7, 1:2. A Figura 17 mostra um talude escavado em solo no Km 06
da BR-174

97. 91
Figura 16: Taludes escavados em rocha em uma mina de calcário
Foto: Bento, 1993.
Figura 17: Talude escavado em solo no Km 06 da BR-174
Foto: Bento, 1998.

98. 92
4.1 CÁLCULO DE VOLUMES
Dependendo do estado do material no processo de terraplanagem, temos
três medidas de volumes:
a) Material no corte ( metro cúbico no corte ): refere-se ao material no
estado natural;
b) Material solto ( metro cúbico solto ): refere-se ao material revolvido que
sofreu empolamento no processo de escavação e transporte;
c) Material compactado ( metro cúbico compactado ): refere-se ao material
que foi compactado e portanto sofreu uma redução de volume devido a
redução dos vazios entre grãos. Nos exemplos a seguir, não faremos
distinção do tipo de volume envolvido
O cálculo de volumes, a partir da planta, de materiais envolvidos no
processo de terraplanagem, pode ser feito por dois métodos:
4.1.1 Método dos perfís paralelos equidistantes
4.1.2 Método das curvas de nível
4.1.1 MÉTODO DOS PERFÍS PARALELOS EQUIDISTANTES
O método dos perfís consiste em desenhar perfís cobrindo a área
abrangida pela terraplanagem. Em seguida, determina-se em cada perfil os
limites da escavação ou aterro e calcula-se a área correspondente. A partir
do conhecimento das áreas de cada perfíl, calcula-se a área média de dois
perfis consecutivos e, em seguida, multiplicando-se pela distância entre
eles, acham-se os volumes parciais. Estes volumes somados corresponde ao
volume total da escavação ( Figura 18 ).

99. 93
Na Figura 18 temos as curvas de nível de um morro, cujo pico está
na cota 45. Vamos partir da hípotese de sua remoção para estabelecimento
de uma plataforma na cota 10. O volume de material a ser removido poderá
ser calculado pelo método dos perfís. Assim, traçam-se os perfís P1, P2 e
P3 distantes entre sí de 20 metros. Determinam-se as áreas abrangidas pelo
processo de terraplanagem que no nosso exemplo são as áreas A1, A2 e A3
( hachuradas ) correspondentes aos respectivos perfís. No passo seguinte
calculam-se as áreas médias da seguinte maneira:
Figura 18: Cálculo de volumes pelo método dos perfís
Área média entre perfís 1 e 2 =
2
21 AA +
= Am1,2
Área média entre perfís 2 e 3 =
2
32 AA +
= Am2,3
Terminado o cálculo das áreas médias, calculam-se os volumes
parciais, isto é, os volumes entre perfís através do seguinte procedimento:
Volume parcial entre perfís 1 e 2 = V1,2 = Am1,2 x 20m

100. 94
Volume parcial entre perfís 2 e 3 = V2,3 = Am2,3 x 20m
O volume total ( Vt ) será a soma dos volumes parciais:Vt= V1,2 + V2,3
EXERCÍCIO
Calcular o volume de material a ser removido no exemplo da Figura
18, admitindo que as áreas A1, A2 e A3 são 50m2
, 150m2
e 45m2
respectivamente e que a equidistância entre os perfís seja de 50 metros.
4.1.2 MÉTODO DAS CURVAS DE NÍVEL
O método das curvas de nível é semelhante ao método dos perfís. A
diferença é que neste método não há necessidade de desenharmos perfís,
uma vez que as áreas compreendidas pela escavação estão delimitadas
pelas curvas de nível ( Figura 19 ). Esta figura refere-se a remoção de um
morro até o estabelecimento de uma plataforma na cota 20 ( plataforma B-
C do perfil 2 ). Ainda no perfil 2 vemos que a porção do morro a ser
removida está delimitada pela linha tracejada. As áreas A1, A2 e A3 são as
delimitadas pelas curvas de nível de cotas 20, 30 e 40 respectivamente.
Calculam-se estas áreas com a utilização do planímetro polar de Amsler
( método mecânico ). Após o cálculo das áreas, calculam-se os volumes
parciais e totais de forma semelhante ao método dos perfis. Para o cálculo
do volume de material àcima da curva de nível 40, teremos que considerar
a área no topo do morro igual a zero, que seria a área A4.

101. 95
Figura 19: Cálculo de volumes pelo método das curvas de nível
xE
AA
V
2
21
2,1
+
= ; xE
AA
V
2
32
3,2
+
= ; xE
AA
V
2
43
4,3
+
=
4,33,22,1 VVVVt ++= , onde A1, A2, A3, A4 são as áreas planimetradas inscritas
nas curvas de nível de cotas 20, 30 e 40, sendo a área A4 igual a zero, uma
vez que corresponde ao topo do morro, onde a interseção do plano de cota
45 com a superfície do relevo fica reduzida a um ponto.
Nas expressões que dão os volumes parciais entre curvas de nível, o
valor “E” que multiplica as áreas médias corresponde à equidistância entre
as curvas de nível, que no nosso exemplo corresponde 10m. No cálculo do
volume àcima da curva de nível 40, o valor “E” passa a ser 5m.

102. 96
4.2 TRAÇADO DA LINHA DE OFF-SET DE UM TALUDE
A Figura 20 mostra na seção “b” as curvas de nível de um morro
variando de 10 a 65 metros ( topo do morro ). Vamos admitir que este
morro deverá ser cortado para implantação, na cota 10, do leito carroçável
de uma rodovia. Para facilitar, vamos admitir que o corte será efetuado em
um único lance e que o talude será de 2:1. Os segmentos de reta r-s e t-u
constituem as laterais esquerda e direita da rodovia na cota 10. O
procedimento para o traçado da linha de off-set é o descrito a seguir:
a) Traça-se uma perpendicular, no ponto “w” ( parte c da Figura 20 ), ao
segmento r-s e obtemos a linha de cota 10, que é a cota de implantação do
leito carroçável;
b)Traçam-se paralelas à primeira perpendicular espaçadas de 10 metros.
Este espaçamento corresponde ao das curvas de nível e deverão ser
traçadas todas as paralelas correspondentes a todas as cotas do morro a ser
recortado;
c) Com o transferidor centrado em “w” e zerado na perpendicular, marca-se
o ângulo de inclinação do talude 2:1 = 63o
26’05”, obtendo-se o segmento
w-m que é o rebatimento do talude. Podemos também obter este segmento
a partir do complemento do ângulo do talude com o transferidor zerado no
segmento r-s;
d) A partir dos pontos de interseção do segmento w-m com as paralelas à
perpendicular em “w”, traçam-se paralelas a r-s. Estas paralelas, juntamente
com a linha da lateral esquerda do leito carroçável na cota 10, são as linhas
de cota 20, 30, 40, 50 e 60 que percorrem a face do talude. A interseção
delas com as curvas de nível correspondentes, determina os off-sets a, b, c,

103. 97
d, e, f, g, h, i, j. A linha que une todos estes pontos define os limites de
corte, isto é, a interseção do plano do talude com a superfície topográfica.
O procedimento para o traçado da linha de off-set do lado direito é o
mesmo aplicado para o lado esquerdo e que acabamos de descrever.
O perfil A-B, parte “a”da Figura 20, mostra em hachuras e com os
limites tracejados, a seção do morro que deverá ser removida. O volume do
material escavado poderá ser calculado pelo método dos perfís, que neste
caso é o mais adequado.
Figura 20: Traçado da linha de off-set

104. 98
EXERCÍCIOS
1 ) Com um teodolito estacionado em uma estaca 01, foram efetuadas as
seguintes leituras em uma mira situada na estaca 02, e as correspondentes
leituras de ângulos zenitais:
γ1 = 86o
20’30”
γ2 = 84o
30’40”
l1 = 1200mm
l2 = 450mm
Com base nestes dados, determinar a distância entre as duas estacas e a
cota da estaca 02, sabendo-se que a declividade entre ambas é de 20% e a
cota da estaca 01 é de 52,540m.
2 ) Com relação a questão 01, qual é a coordenada da estaca 02, sabendo-se
que a da estaca 01 é 100m Este e 100m Norte e que o azimute da estaca 01
para a estaca 02, Az1,2 é de 125o
37’42”?
3 ) O levantamento topográfico planialtimétrico de um terreno apresentou
os dados de campo constantes da tabela abaixo:
A. A. Estaca Estaca Azimute A.Vertical A.Vertical L.Estádia L.Estádia
1500mm 1 2 26
o
42’30” 86
o
41’50” 86
o
13’20” 700mm 1000mm
1600mm 2 3 93
o
13’20” 89
o
53’20” 89
o
32’30” 1400mm 1700mm
1650mm 3 4 212
o
19’30” 91
o
40’ 00” 91
o
18’00” 2400mm 2700mm
1570mm 4 1 283
o
45’30” 90
o
35’20” 90
o
10’30” 2200mm 2500mm
A.A. = Altura do Aparelho
A. Vertical = Ângulo Vertical
L. Estádia = Leitura na Estádia

105. 99
Com base nestes resultados, responda as seguintes questões:
a )Qual é o perímetro do terreno?
b) Quais são as altitudes das estacas 2, 3 e 4 admitindo a altitude de 52,50m
para a estaca 1?
c ) Qual o erro linear relativo cometido no levantamento do terreno?
d ) Qual a área do terreno?
e ) Qual o comprimento das duas diagonais do terreno?
4) A planilha de levantamento topográfico da página seguinte, é referente a
uma poligonal com 12 vértices. A partir dos dados desta planilha, calcule:
a) O erro linear absoluto cometido no levantamento;
b) O erro linear relativo cometido no levantamento;
c) Os ângulos internos da poligonal;
d) O erro angular cometido no levantamento;
e) As coordenadas finais dos vértices da poligonal;
f) A área do terreno delimitado pela poligonal;
g) Desenhar a poligonal na escala 1:400.

106. 100
5 NOÇÕES DE GEODÉSIA
O estudo da forma e dimensões da Terra é feito pela Geografia
Matemática que compreende a Topografia, Geodésia e a Astronomia de
Posição. A Geografia Matemática é uma generalização da Geodésia e da
Cartografia, ocupando-se a Geodésia com o estudo da forma e dimensões
da Terra, e a Cartografia da representação da Terra em um plano, que é o
plano geodésico onde se configuram suas formas e dimensões. A
Topografia nada mais é que uma forma didática de se iniciar o estudo da
Geografia Matemática, portanto da Geodésia e Cartografia, onde as formas
e dimensões da Terra são representadas no plano topográfico, que é um
caso particular do plano Geodésico.
Assim, em topografia são estudados os processos de medição e
normas para a representação de uma região de extensão limitada da
superfície da Terra sobre um plano convencional, o plano topográfico de
projeção. Os processos de medição são estudados sob o título de
Topometria que compreende a Planimetria, onde são efetuadas medidas
lineares e angulares num plano horizontal, e a Altimetria onde são
efetuadas medidas lineares e angulares num plano que contém a vertical do
lugar definida pelo fio de prumo.
Na topografia as normas para representação da superfície da Terra
compreendem: a projeção dos pontos da superfície da Terra, segundo a
vertical do lugar, sobre o plano Topográfico de projeção e a sua
representação convencional; redução das dimensões do plano Topográfico
para as dimensões limitadas de uma folha de papel, segundo a escala
adotada, resultando na planta Topográfica da região.
Na Geografia Matemática estudam-se os processos de medição e
normas para representação até de toda a superfície terrestre, sobre uma

107. 101
superfície convencional próxima da superfície de nível médio dos mares,
que é a do Geóide. Esta superfície de referência com um só parâmetro é
uma esfera de raio definido; com dois parâmetros conhecidos ( semi-eixos
“a” e “b” ), é o Elipsóide Internacional de Referência. No sistema de
projeção plana ( U.T.M.) para representação da superfície da Terra, adota-
se o Elipsóide Internacional de Hayford, cujos semi-eixos estão na página
2.
As áreas da Geografia Matemática nas quais são estudados os
processos de medição compreendem a Topometria, que apresenta as
mesmas divisões da Topografia, a Gravimetria ou Geodésia Dinâmica e a
Astronomia de Posição ou Geodésica. Na Topometria são estudados os
processos de medição e cálculo da posição de pontos da superfície
topográfica em relação à superfície abstrata do Elipsóide de Referência. Na
Gravimetria estudam-se: processos de medição ou determinação da
aceleração da gravidade; formas de estabelecer relações entre a superfície
abstrata do Geóide e a do Elipsóide de Referência; formas de calcular os
afastamentos entre pontos do Geóide e a superfície do Elipsóide de
Referência, sendo estes pontos definidos por suas coordenadas geográficas
e geodésicas, isto é, Latitude, Longitude e Azimute. Na Astronomia de
Posição estudam-se os processos de medição ou determinação das
coordenadas geográficas astronômicas, que fornecem a posição de pontos
de referência na superfície da Terra, com apoio na esfera celeste. Estas
coordenadas astronômicas são referidas à superfície real e iregular da
Terra, ou seja, o Geóide; quando a referência é a superfície convencional e
regular do Elipsóide Internacional de Hayford, temos então as coordenadas
geodésicas. Nos pontos de referência sobre a superfície da Terra é que se
apoiam os levantamentos topográficos ou geodésicos.

108. 102
As normas de representação da superfície da Terra no plano
geodésico, em Geografia Matemática, são estudadas pela Cartografia que
utilizando conceitos matemáticos procura estabelecer, sempre que possível,
uma correspondência biunívoca entre pontos da superfície topográfica ou
do Geóide e os pontos correspondentes no plano geodésico. Deste modo
podemos representar até toda a superfície da Terra por meio de expressões
matemáticas que possibilitam conhecer as coordenadas planas X e Y de
pontos representativos sobre o plano geodésico, em função dos respectivos
pontos da superfície topográfica da Terra, ou do Geóide, definidos por sua
latitude, longitude e Afastamento ( distância vertical em relação ao
Elipsóide ) ou Altitude ( distância vertical em relação ao Geóide ).
A redução das dimensões das coordenadas XY calculadas sobre o
Elipsóide, para as dimensões de uma folha de papel, permite o desenho dos
pontos representativos, constituindo a Carta topográfica ou geográfica da
região ou de toda a superfície da Terra.
5.1 TRANSPORTE DE COORDENADAS
O transporte das coordenadas ou determinação das coordenadas dos
pontos das redes geodésicas é feito por cálculos sucessivos de triângulos,
partindo-se de um ou mais lados medidos e calculados com rigor, e do
valor de ângulos medidos também com técnica e rigor estabelecidos. As
redes geodésicas servem de apoio aos trabalhos de mapeamento e auxiliam
as pesquisas sobre a forma e propriedades físicas da Terra. Ela é constituída
por um conjunto de figuras amarradas entre si, destacando-se como mais
frequentes ( Figura 21 ): quadrilátero simples com duas diagonais (a),
pentágono com ponto central (b), hexágono com ponto central (c),
triângulo simples (d) e triângulo com ponto central (e). Na realidade, todas

109. 103
estas figuras são constituídas por um conjunto de triângulos que facilitam
então o transporte de coordenadas, daí o nome que se dá ao método de
TRIANGULAÇÃO.
Figura 21: Figuras mais frequentes das redes geodésicas.
5.1.1 CLASSIFICAÇÃO DAS TRIANGULAÇÕES
As triangulações são classificadas com base na precisão das medidas
e dos resultados dos cálculos, nas seguintes ordens de precisão de acordo
com as Normas Gerais da Diretoria de Serviço Geográfico do Exército
( DSG ):
a) Triangulação de primeira ordem com as seguintes especificações:
-Erro médio na medida das bases = 1:1.000.000
-Erro final = 1:300.000
-Comprimento médio dos lado = 20km

110. 104
-Erro médio de fechamento dos triângulos = 1”
-Erro máximo num triângulo isolado = 3”
b) Triangulação de segunda ordem com as seguintes especificações:
-Erro médio na medida das bases = 1:500.000
-Erro final = 1:150.000
-Comprimento médio dos lado = 10 a 20km
-Erro médio de fechamento dos triângulos = 3”
-Erro máximo num triângulo isolado = 6”
c) Triangulação de terceira ordem com as seguintes especificações:
-Erro médio na medida das bases = 1:250.000
-Erro final = 1:75.000
-Comprimento médio dos lado = 5 a 15km
-Erro médio de fechamento dos triângulos = 6”
-Erro máximo num triângulo isolado = 9”
Nas triangulações, para evitar o acúmulo de erros angulares,
determina-se em determinados pontos, com certa precisão, azimutes
considerados fixos. Estes são os pontos ou estações de Laplace, onde as
latitudes e os azimutes são determinados astronomicamente ( referidos ao
Geóide ). Para seu uso nas triangulações, há necessidade de transformá-los
em azimutes geodésicos ou de Laplace ( referidos ao Elipsóide ). Estes
azimutes são os azimutes astronômicos com a correção do desvio da
vertical, ou seja, a diferença angular entre a normal ao Geóide e a normal
ao Elipsóide. A conversão de um azimute no outro é feita com a utilização
da equação de Laplace:
Azg = Aza + ( λa - λg ).senϕg, onde:
Azg = azimute geodésico ou de Laplace
Aza = azimute astronômico

111. 105
λa = longitude astronômica
λg = longitude geodésica
ϕg = latitude geodésica
5.1.2 TRIANGULAÇÃO GEODÉSICA
Na operação de transporte de coordenadas no elipsóide ou no plano,
efetua-se em primeiro lugar o cálculo dos triângulos que constituem a
estrutura básica da triangulação, determinando-se os valores dos seus
ângulos e o comprimento dos lados.
Nas triangulações sobre o elipsóide, a superfície elipsóidica pode ser
substituída pela de uma esfera de curvatura média, o que permite o cálculo
dos triângulos como se fossem triângulos esféricos, uma vez que os
triângulos geodésicos medidos podem ser tratados como triângulos
desenvolvidos sobre a superfície de uma esfera. É comprovado que o erro
máximo resultante desta conversão de triângulos geodésicos em triângulos
esféricos, é de 1 centímetro na medida dos lados, e nas condições mais
desfavoráveis. Para resolução destes triângulos, aplica-se o teorema de
LEGENDRE. Segundo este teorema, os triângulos esféricos de lados muito
pequenos em relação ao raio da Terra, podem ser substituídos por
triângulos planos de lados equivalentes, devendo-se efetuar a subtração de
3
1
do excesso esférico de cada um de seus ângulos.
Fica claro que o conhecimento do excesso esférico é fundamental
nos trabalhos de triangulação geodésica.

112. 106
5.1.3 DETERMINAÇÃO DO EXCESSO ESFÉRICO
Tomemos como exemplo a esfera da Figura 21 seccionada por três
planos perpendiculares entre sí: DEF, GEH e DHF.
Figura 21: Esfera seccionada por três planos perpendiculares entre sí.
A esfera fica dividida em duas semi-esferas contendo cada uma 4
triângulos esféricos. Estes triângulos são TRIRETÂNGULOS, uma vez que
seus vértices são definidos pelas interseções dos planos. Desta forma,
temos como soma dos ângulos internos de cada triângulo esférico o valor
de 270º
, ou seja:
∑γi = γ1 + γ2 + γ3 = 90o
+ 90o
+ 90o
= 270o
, onde γi são os ângulos internos
do triângulo esférico. Comparando-se esta soma dos ângulos internos de
um triângulo esférico com a soma dos ângulos internos de um triângulo
plano, veremos que existe um diferencial que corresponde ao excesso
esférico Ε, ou seja:
Ε = ∑γi - ∑αi = ∑γi – (n-2).180o
= 270o
– 180o
= 90o
, onde:
αi = ângulos internos do triângulo plano;
n = número de lados do triângulo = 3

113. 107
Por conseguinte, resulta que qualquer poligonal planimétrica
acumula um erro sistemático de fechamento angular correspondente a
Ε = ∑γi - ∑αi = ∑γi – (n-2).180o
, o qual não deve ser confundido com os
erros acidentais e grosseiros cometidos no levantamento.
Em consequência do excesso esférico, a condição de fechamento
angular nas triangulações geodésicas, fica estabelecida pela seguinte
expressão:
εa = ∑xi – ( 180o
+ Ε ), onde xi são os ângulos internos medidos. Para um
erro angular igual a zero, teremos:
Ε = ∑xi – 180o
, isto é, em não havendo erro angular, a subtração de 180o
da
soma dos ângulos medidos, será o próprio excesso esférico.
Retomando a nossa esfera seccionada pelos três planos
perpendiculares entre sí, verifica-se que a sua superfície abriga 8 triângulos
triretângulos, visto que cada metade está coberta por 4 deles. Posto que
cada triângulo possui um excesso esférico de 90o
, então a superfície
esférica possuí uma esfericidade de 720o
, ou seja: 8 x 90o
= 720o
. O
conhecimento deste excesso esférico da esfera, permite o cálculo do
excesso esférico de qualquer outra superfície, através da seguinte operação:
2
4
720
Rπ
°
=
Α
Ε
29577951,57.
4
720.
22
RR
Α
=Ε⇒
°Α
=Ε⇒
π
em graus sexagesimais,
onde: A = superfície que se pretende determinar o excesso esférico;
R = raio da Terra na região considerada.
Para calcularmos o excesso esférico em minutos e segundos de grau,
substitui-se o parâmetro 57,29577951, por 3437,746771 ou por
206264,8062 respectivamente.

114. 108
As poligonais com excesso esférico inferior a 0,1” (
10
1
de segundo ),
consideram-se como poligonais planas ou topográficas. Por outro lado,
aquelas com excesso esférico superior consideram-se como poligonais
geodésicas.
5.2 TRILATERAÇÃO
Na impossibilidade ou dificuldade para medição angular, devido a
existência de nevoeiro, fumaça, impossibilidade de estacionar o
equipamento em um ou mais vértices, usa-se a TRILATERAÇÃO. Ela
consiste no controle geodésico horizontal, mediante a medição do
comprimento de lados de triângulos.
A figura básica da trilateração é um hexágono ou um duplo
quadrilátero com todas as diagonais e lados medidos ( Figura 21 ). Resulta
então nove diagonais para o hexágono e seis diagonais para o duplo
quadrilátero.
Figura 22: Figuras básicas da trilateração: hexágono (a),
duplo quadrilátero (b).

115. 109
5.3 CONVERGÊNCIA MERIDIANA
É importante a determinação da convergência meridiana para
transformação dos azimutes geodésicos em azimutes planos e vice-versa.
Em consequência da convergência meridiana, o alinhamento Norte-
Sul ( direção do meridiano local ) em um determinado ponto sobre a
superfície da Terra, não é paralelo ao mesmo alinhamento em um outro
ponto. Isto porque, como sabemos, os meridianos convergem para os polos
onde a falta de paralelismo é mais acentuada.
No Sistema U.T.M. ( Universal Transverse Mercator ) de projeção
plana, a superfície terrestre é dividida em 60 fusos com amplitude de 6o
em
longitude. Cada fuso representa um sistema de eixos cartesianos XY sobre
o plano geodésico, o qual resulta do desenvolvimento de um cilindro
tangente e transversal ao meridiano central do fuso. Este meridiano fica
representado no plano geodésico em verdadeira grandeza. A convergência
meridiana em um determinado ponto sobre a superfície terrestre é, então, o
ângulo que a tangente ao meridiano terrestre neste ponto, forma com a
paralela ao meridiano central do fuso U.T.M. ( Figura 23 ). Nesta figura,
temos:
P = ponto sobre a superfície da Terra;
NQ = paralela ao meridiano central no ponto P, ou Norte da Quadrícula
U.T.M.;

116. 110
θ = Convergência meridiana
Figura 23: Convergência meridiana
No hemisfério Norte, a oeste do meridiano central a convergência é
negativa, ao passo que a leste do meridiano central ela é positiva; no
hemisfério Sul, a oeste do meridiano central ela é positiva, enquanto que a
leste ela é negativa.
A amplitude da convergência meridiana varia com a latitude e a
longitude do ponto considerado, e o seu valor pode ser calculado a partir da
seguinte expressão:
2
sec.sen.
La
LamLg
∆
∆=θ , onde:
∆Lg = diferença de longitude entre os dois pontos considerados;
Lam = latitude média ( média aritmética entre as latitudes dos dois pontos
considerados );
∆La = diferença de latitude entre os dois pontos considerados.

117. 111
Os valores de ∆Lg e ∆La podem ser calculados através da expressão
que fornece o resultado em segundos:
∆Lg =
R
X
π
3600.180.∆
∆La=
R
Y
π
3600.180.∆
, onde ∆X e ∆Y são as diferenças de abcissas e
ordenadas, respectivamente, entre os dois pontos considerados e R o raio da
Terra na região.
Por outro lado, se desejamos saber o comprimento do arco de
circunferência entre dois pontos situados sobre a superfície da Terra, a
partir do conhecimento das suas latitudes e longitudes, utiliza-se a seguinte
expressão:
CosS = cos∆Lg.cos∆La + sen∆Lg.sen∆La, onde S é o arco de circunferência
entre os dois pontos expresso em graus. O seu comprimento será calculado
através da equação seguinte:
180
arccos.. SR
L
π
= , onde L é igual ao comprimento do arco de circunferência
entre os dois pontos.
Em projetos de linhas de transporte ( rodovias, ferrovias, linhas de
transmissão, etc...), temos que levar em consideração que estamos
trabalhando sobre a superfície curva da Terra, o que requer a determinação
da convergência meridiana nos pontos extremos ou a intervalos de
distâncias razoáveis (10km ) para checagem dos azimutes e contrôle de erro
na poligonal aberta resultante. Esta convergência deverá ser somada ou
subtraída das determinações do Norte verdadeiro, que é feita por
observações astronômicas de precisão.

118. 112
EXERCÍCIOS
Em todos os exercícios a seguir, adotar o valor de 6.371km para o
raio da Terra.
1) Qual o excesso esférico de um triângulo geodésico, equilátero, cujo lado
tem o comprimento de 30km?
2) Qual a área que pode ser levantada por um teodolito com precisão de 1’
( um minuto ) na leitura dos ângulos azimutais, sem que se faça
perceber a curvatura da Terra?
3) Qual a convergência meridiana entre dois pontos sobre a superfície da
Terra que possuem as longitudes de 23o
30’30”, 22o
25’40” e as
latitudes de 20o
10’20”, 20o
15’18”?
4) Qual a convergência meridiana entre dois pontos sobre a superfície da
Terra que possuem as ordenadas de 8.240m, 16.400m e as abcissas de
5.500m e 12.700m? Adotar o valor de 6.371km para o raio da Terra.
5) Qual a distância e a convergência dos meridianos entre dois pontos
situados sobre a superfície da Terra cujas latitudes e longitudes são as
seguintes:
Ponto 1: Latitude = 23o
42’10”; Longitude = 46o
35’30”
Ponto 2: Latitude = 21o
32’05”; Longitude = 42o
20’35”

119. 113
6 EXEMPLO DE UM LEVANTAMENTO TOPOGRÁFICO
O Anexo A é uma planta do levantamento topográfico de uma
propriedade situada no bairro de São José, município de Manaus-AM,
compreendida pelas latitudes e longitudes U.T.M. ( Universal Transverse
Mercator ) de 9.658.470m Norte - 9.658.850m Norte e 169.035m Este -
169.115m Este respectivamente. Neste levantamento foi utilizado um
Teodolito Nikon Modelo NE-20H com precisão angular de 10”. O
procedimento adotado foi o seguinte:
1) Reconhecimento preliminar do terreno;
2) Estabelecimento de uma poligonal de apoio constituída de 12 vértices e
execução do seu levantamento por caminhamento;
3) Amarração dos vértices do terreno, também num total de 12, aos vértices
mais próximos da poligonal de apoio, por irradiação;
4) Cadastramento a partir dos vértices da poligonal de apoio mais próximos
aos detalhes por irradiação;
5) Cálculo do erro de fechamento da poligonal de apoio;
6) Distribuição do erro de fechamento, proporcional às coordenadas e
cálculo das coordenadas coorigidas;
7) Cálculo das coordenadas finais dos vértices da poligonal, a partir das
coordenadas U.T.M. do seu vértice 01. A coordenada U.T.M. foi obtida
com um G.P.S.;
8) Cálculo das coordenadas finais dos vértices da divisa do terreno a partir
do respectivo vértice de irradiação da poligonal de apoio;
9) Cálculo dos azimutes e comprimentos dos lados do terreno a partir das
suas coordenadas finais;
10) Desenho da planta em escala 1:400 ( Anexo A ).

120. 114
7 MEMORIAL DESCRITIVO
O memorial descritivo é a peça que encerra a descrição do perímetro
da propriedade. Basicamente contém indicações dos azimutes,
comprimento dos alinhamentos entre marcos da divisa e nome dos
confrontantes. Nas linhas a seguir, temos exemplos de 3 modelos de
memoriais descritivos.
7.1 MODELO I DE MEMORIAL DESCRITIVO
O imóvel tem as seguintes características e confrontações: Trata-se
de um lote de terras denominado “Descanso do Descansado”, situado à
margem da rodovia BR-001, sem número, nesta cidade, com uma área total
de 19.570,00 m2
( dezenove mil quinhentos e setenta metros quadrados ),
delimitado por um polígono cujo perímetro mede 485,00 m ( quatrocentos
e oitenta e cinco metros lineares ), tendo como limite norte a interseção dos
limites oeste e leste ( estaca 3 ); ao Sul, com terras ocupadas e beneficiadas
por Joaquim Zanzóis Carapulsa, por uma linha de 110,00 m ( cento e dez
metros lineares ), no azimute de duzentos e cincoenta graus ( 250o
), Estaca
1-2 ; a leste, para onde faz frente, com a referida rodovia, por uma linha de
185,00 m ( cento e oitenta e cinco metros lineares ), no azimute de cento e
quarenta e seis graus ( 146o
), Estaca 3-1; a oeste, com terras ocupadas por
Pedro Pereira Pedreira Pinto, por uma linha de 190,00 m ( cento e noventa
metros lineares ), no azimute de trezentos e sessenta graus ( 360o
), Estaca
2-3, medindo o referido lote, de frente, em linha reta, 185,00 m ( cento e
oitenta e cinco metros lineares ).

121. 115
7.2 MODELO II DE MEMORIAL DESCRITIVO
Terreno situado na Avenida Biscoito-Duro, número 380 ( trezentos e
oitenta ), nesta cidade, com uma área de 2.105,58 m2
, delimitada por um
perímetro de 187,50 m ( cento e oitenta e sete metros lineares e 50
centímetros ), com os seguintes limites e confrontações: ao norte, com o
Beco laranja-azeda; a leste, com a Avenida Biscoito-Duro, para onde faz
frente; ao sul, com imóvel pertencente à Janjão Jato Jibóia; finalmente, a
oeste, com terras de Filisberta Felícia Feliz.
O perímetro apresenta a seguinte descrição: partindo da Estaca 1,
definida pela coordenada geográfica de latitude 3o
05’22,07’’ Sul e
longitude 60o
01’25,56’’ WGr , correspondentes as coordenadas UTM (
Elipsóide SAD 69 ) 9.568.056,602 m Norte e 830.852,290 m Leste,
referida ao meridiano central 63o
WGr, seguindo com azimute de 175o
07’25’’ e distância de 24,81 metros, chega-se na Estaca 2; desta seguindo
com o azimute de 176o
54’32’’ e distância de 21,77 metros, chega-se na
Estaca 3; desta, seguindocomo azimute de 176o
54’41’’ e distância de 5,00
metros, chega-se na Estaca 4; desta, seguindo com azimute de 267o
32’12’’
e distância de 36,86 metros, chega-se na Estaca 5; desta, seguindo com o
azimute de 344o
53’46’’ e distância de 5,09 metros, chega-se na Estaca 6;
desta, seguindo com o azimute plano de 344o
53’55’’ e distância de 22,60
metros, chega-se na Estaca 7; desta, seguindo com o azimute de 269o
47’56’’ e distância de 5,60 metros, chega-se na Estaca 8; desta, seguindo
com o azimute de 3o
44’51’’ e distância de 18,45 metros, chega-se na
Estaca 9; desta, seguindo com o azimute de 84o
32’14’’ e distância de 5,96
metros, chega-se na Estaca 10; desta, seguindo com o azimute de 353o
27’15’’ e distância de 1,91 metros, chega-se na Estaca 11; desta, seguindo

122. 116
com o azimute de 82o
05’09’’ e distância de 39,55 metros, chega-se na
Estaca 1, ponto de partida do perímetro descrito.
7.3 MODELO III DE MEMORIAL DESCRITIVO
O terreno apresenta as seguintes características:
Área: 102, 1329 há (Cento e dois hectares, treze ares e vinte e nove
centiares );
Perímetro: 4.187, 58 m ( Quatro mil, cento e oitenta e sete metros e
cincoenta e oito centímetros );
Localização: Margem direita do Rio Seco;
Município: Pindorama;
Estado: AI.
Limites e Confrontações:
NORTE: Com área remanescente da gleba Amassunum, por uma
linha entre os marcos M17-M01, no Azimute verdadeiro de 50o
12’59’’
na distância de 1.000 metros;
LESTE: Com a margem direita do Rio das Cabras, para onde faz
frente, por quatro linhas entre os Marcos M01, M02, M03, M04 e M05,
nos respectivos Azimutes verdadeiros de 174o
28’24’’, 144o
44’00’’,
135o
06’56” e 126o
06’26’’ e respectivas distâncias de 70,71m, 547,04,
221,01m e 268,67m ;
SUL: Com Joel Jelolej, por uma linha entre os Marcos M05/M06, no
Azimute verdadeiro de 229o
12’32’’, na distância de 978,20 m;

123. 117
OESTE: Com área remanescente da gleba Amassunum, por uma
linha entre os Marcos M16-M17, no Azimute verdadeiro de 318o
57’26’’
na distância de 1.101,95 metros.
QUADRO RESUMO
I. Perímetro
A ) LADO B ) AZIMUTE C ) DISTÂNCIA
M1 – M2 174o
28’24’’ 70,71 metros
M2 - M3 144o
44’00” 547,04 metros
M3 – M4 135o
06’56’’ 221,01metros
M4 – M5 126o
06’26’’ 268,67 metros
M5 – M16 229o
12’32’’ 978,20 metros
M16 – M17 316o
57’26’’ 1.101,95 metros
M17 – M01 50o
12’59’’ 1.000,00 metros

124. 118
BIBLIOGRAFIA CONSULTADA
BARROS, E. G. Curso de GPS: fundamentos de GPS. Manaus: 4a
Divisão de Levantamento, 1995.25p.
BORGES, A. C. Exercícios de Topografia. 3.ed.. São Paulo. Edgard
Blücher, 1975. 192p.
BORGES, A. C. Topografia. São Paulo: Edgard Blücher, 1978. v.1. 187p.
BORGES, A. C. Topografia Aplicada à Engenharia Civil. São Paulo:
Edgard Blücher, 1992. v. 1. 232p.
BREED, C. B. Topografia. Bilbao: Urmo, 1974. 587p. Traduzido por:
Farjas, C. E., Pareja, E. S., Sánchez, L. M., Martin, J. M. M.
CARDÃO, C. Topografia. 4. ed. Belo Horizonte: Engenharia e
Arquitetura, 1970. 509p.
CATERPILLAR TRACTOR Co. Manual de Produção Caterpillar.4a
ed.s.l., 1984.
COMASTRI, J. A. Topografia: Planimetria. 2a
ed. Viçosa: UFV, 1992.
336p.
COMASTRI, J. A., GRIPP JÚNIOR, J. Topografia aplicada. Viçosa:
UFV, 1990.
CORREIA, M. S. O Manual do Topógrafo. 2a
ed. Porto: Lopes da Silva,
1981. 503p.
DAVIS, R. E., FOOTE, F. S., KELLY, J. W. Tratado de Topografia. 3.
ed.. Madrid: Aguillar, 1976. 977p. Traduzido por: Mantero, J. M.
Traduzido de: Surveying Theory and Practice.
DAVIS, R. E., KELLY, J. W. Topografia Elemental. 3. ed. México:
CECSA ( Cia. Ed. Continental S.A ), 1976. 648p. Traduzido por:
Saucedo, J. L. L. Tradução de: Elementary Plane Surveying.

125. 119
ESPARTEL, L. Curso de Topografia. 6. ed. Porto Alegre: Globo, 1978.
655p.
ESPARTEL, L., LÜDERITZ, J. Caderneta de Campo. 11. ed. Porto
Alegre: Globo, 1979. 655p.
GARCIA, G. J., PIEDADE, G. C. R. Topografia Aplicada às Ciências
Agrárias. 5.ed. São Paulo: Nobel, 1984. 256p.
JORDAN, W. Tratado General de Topografia. 9a
ed. Barcelona: Gustavo
Gili, 1961. v.1,2.
LOCH, C., CORDINI, J. Topografia Contemporânea. 20. ed. Santa
Catarina: UFSC, 1995. 320p.
MANAUS. Lei No
1208 de 25 de março de 1975-Código de
Obras.Manaus: Divisão de Informática-URBAM, 1998.
MESQUITA, P. F. Curso Básico de Topografia, Astronomia de Posição
e Geodésia. São Paulo: DLP/EPUSP, 1969. 294p.
MINISTÉRIO DO EXÉRCITO. Manual Técnico T34 – 604 –
Nivelamento Barométrico. Portaria no. 080 – EME, 15/10/1975.
----------------------------------------. Manual Técnico T34-400.
Triangulação e Trilateração Geodésicas. Portaria no. 068-EME,
25/11/1976.
----------------------------------------. Manual Técnico T 34-501. Astronomia
de 2a
ordem. Portaria no. 089-EME, 14/12/1978.
----------------------------------------. Manual Técnico T 34-401.
Poligonação eletrônica. Portaria no. 069-EME, 25/11/1976.
----------------------------------------. Manual Técnico T 34-304.
Aerotriangulação. Portaria no. 082-EME, 27/12/1976.
----------------------------------------. Manual Técnico T 34-500. Astronomia
Expedita. Portaria no. 079-EME, 25/11/1977.
PASSINI, C. Tratado de Topografia. Barcelona: Gustavo Gilli, 1969.

126. 120
PINTO, L. E. Curso de Topografia. Salvador: CED/UFBA, 1988.
PRIMO,B., SOARES, S. M. GPS-Introdução e Aplicações Práticas. s.l:
Luana. s.d.
RAISZ, E. Cartografia Geral. 2. ed. Rio de Janeiro: Científica, 1948.
4l4p. Traduzido de: General Cartography.
RUIZ, J.Z. Topografia Practica. 23ª
ed. Barcelona: CEAC, 1987. 160p.
SILVEIRA, L. C. Cálculos Geodésicos no Sistema UTM aplicados à
Topografia. s.l.Luana.s.d.
TOSCANO, R. Métodos Topográficos.14. ed. México: Porrua, 1977.
923p.