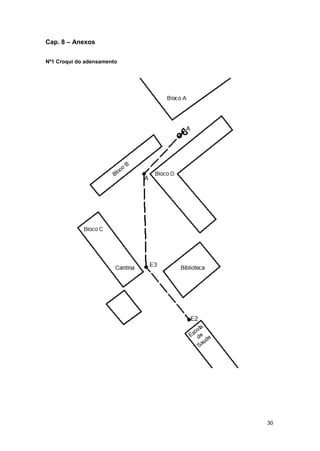
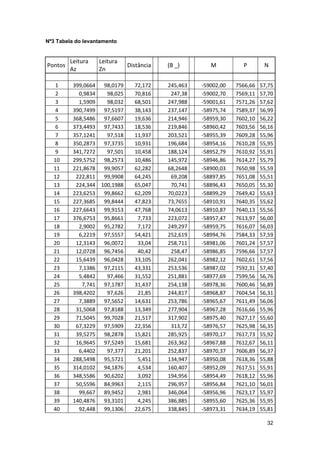
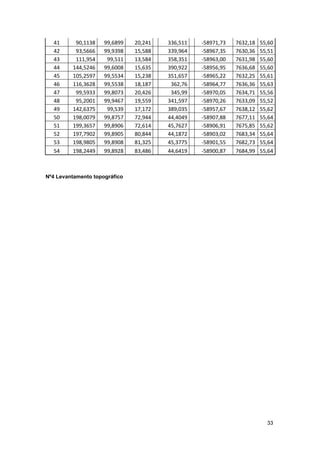
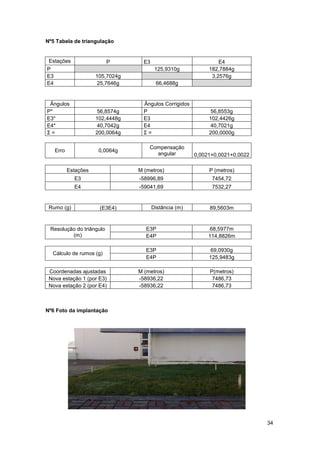
Este relatório descreve cinco aulas de campo de topografia, incluindo adensamento, levantamento topográfico clássico, nivelamento geométrico, triangulação e implantação. Fornece detalhes sobre os objetivos, procedimentos, cálculos e conclusões de cada atividade prática.

1. Relatório
final de
topografia
João Lopes
Nuno Almeida
Susana Ribeiro

2. João Carlos Silva Lopes N.º2103377
Susana Isabel Rosa Ribeiro N.º2110421
Turno: PL1
Nuno Miguel de Figueiredo Almeida N.º2110760

3. I
Índice
CAP. 1 – INTRODUÇÃO............................................................................................................... 6
CAP. 2 – ADENSAMENTO (Irradiação)........................................................................................ 8
2.1 – Objectivos ......................................................................................................................... 8
2.2 – Procedimentos e Cálculos................................................................................................ 9
2.3 – Conclusão....................................................................................................................... 13
CAP 3 – LEVANTAMENTO TOPOGRÁFICO CLÁSSICO ......................................................... 13
3.1 – Objetivos......................................................................................................................... 13
3.2 – Procedimentos e Cálculos.............................................................................................. 14
3.3 – Conclusões ..................................................................................................................... 16
CAP. 4 – NIVELAMENTO GEOMÉTRICO ................................................................................. 16
4.1 – Objectivos ....................................................................................................................... 16
4.2 – Procedimentos e Cálculos.............................................................................................. 18
4.3 – Conclusões ..................................................................................................................... 21
CAP. 5 – TRIANGULAÇÃO......................................................................................................... 22
5.1 – Objectivo......................................................................................................................... 22
5.2 – Justificação dos cálculos ................................................................................................ 22
5.3 – Conclusão....................................................................................................................... 25
Cap. 6 – IMPLANTAÇÃO ............................................................................................................ 25
6.1 – Objetivos......................................................................................................................... 25
6.2 – Procedimentos e Cálculos.............................................................................................. 25
6.3 – Conclusões ..................................................................................................................... 29
Cap. 7 – Conclusões finais.......................................................................................................... 29
Cap. 8 – Anexos.......................................................................................................................... 30
Nº1 Croqui do adensamento ................................................................................................... 30
Nº2 Foto aérea com indicação dos pontos.............................................................................. 31
Palavras - Chave...........................................................................................................................III
Índice de tabelas ...........................................................................................................................IV
Índice de figuras ............................................................................................................................IV
Resumo ........................................................................................................................................ III
Acrónimos.....................................................................................................................................IV

4. Nº3 Tabela do levantamento ................................................................................................... 32
Nº4 Levantamento topográfico ................................................................................................ 33
Nº5 Tabela de triangulação ..................................................................................................... 34
Nº6 Foto da implantação ......................................................................................................... 34
Nº7 Trabalho em suporte digital (CD)...................................................................................... 35
II

5. Resumo
No âmbito desta Unidade Curricular, tivemos a oportunidade de testar no terreno as nossas
aprendizagens teóricas, ou seja, tivemos 5 aulas de campo, onde em cada uma delas
colocámos em prática conceitos diferentes, que aprendemos nas aulas teóricas, ficando assim
com uma melhor percepção da área que é a Topografia, bem como do manuseamento dos
seus equipamentos.
Este relatório é, portanto, uma descrição dessas aulas de campo, com os devidos comentários
e apreciações que achámos serem mais relevantes.
A primeira dessas aulas tratou-se apenas de uma “apresentação” física aos equipamentos e
aos seus métodos de utilização e será incluída no Capítulo 2, as quatro restantes serão
descritas nos Capítulos 2,3,4,5 e 6.
Palavras - Chave
Adensamento
Alidade
Altimetria
Ângulos azimutais
Ângulos Zenitais
Bastão
Bessel
Bolha de nível
Bonne
Clarke
Coordenadas planimétricas
Cotas
Data
Datum
Declive
Distanciómetro electrónico
Elipsóide
Estação total
Fotogrametria
Gauss-Kruger
Geóide
GPS
GRS80
Hayford
Implantação
Intersecções
Irradiação
Latitude
Leitura inversa
Leituras azimutais
Leituras corrigidas
Leituras directas
Leituras zenitais
Levantamento topográfico
Longitude
Luneta
Mercator
Meridiana
Método da irradiação
Mira topográfica
Nível digital
Nivelamento
Norte Cartográfico
Parafusos calantes
Perpendicular
Planimetria
Poligonação
Prisma
Projecção Cartográfica
Rede geodésica
Rumo
Triangulação
Tripé
Vértices geodésicos
III

6. GPS – Global Positioning System (sistema de posicionamento global)
Índice de tabelas
Tabela 1 - data geodésicos........................................................................................................... 7
Tabela 2 - leituras do adensamento............................................................................................ 10
Tabela 3 - leituras corrigidas do adensamento........................................................................... 11
Tabela 4 - coordenadas planimétricas dos pontos conhecidos.................................................. 11
Tabela 5 - quadrantes (para acertos no cálculos dos rumos)..................................................... 12
Tabela 6 - dados (para levantamento) ........................................................................................ 14
Tabela 7 - leituras do nivelamento .............................................................................................. 18
Tabela 8 - nivelamento geométrico............................................................................................. 19
Tabela 9....................................................................................................................................... 22
Tabela 10..................................................................................................................................... 22
Tabela 11..................................................................................................................................... 22
Tabela 12 - dados para implantação........................................................................................... 26
Tabela 13 - calculo de aterro ou escavação ............................................................................... 26
Tabela 14 - dados da implantação.............................................................................................. 27
Tabela 15 - cálculo de escavação ou aterro ............................................................................... 28
Índice de figuras
Figura 1 – elipsóide e geóide ........................................................................................................ 6
Figura 2 - tripé ............................................................................................................................... 8
Figura 3 - estação total.................................................................................................................. 8
Figura 6 - nivelamento do tripé...................................................................................................... 9
Figura 7 - fixação das pernas do tripé........................................................................................... 9
Figura 8 - visor da estação............................................................................................................ 9
Figura 9 - rumo de E3 para E2.................................................................................................... 11
Figura 10 - (E3 E2) é igual ao R0 ................................................................................................ 12
Figura 11 – nível ótico ................................................................................................................. 16
Figura 12 - régua......................................................................................................................... 16
Figura 13 - nivelamento geométrico............................................................................................ 17
Figura 14 - nivelamento composto.............................................................................................. 17
Figura 15 - nivelamento e contra nivelamento............................................................................ 18
Figura 16 - distancias do nivelamento ........................................................................................ 21
Figura 17 - leituras a partir de P (triangulação)........................................................................... 23
Figura 18 - triangulo resolvido (triangulação).............................................................................. 24
IV
Acrónimos
Figura 4 - bastão........................................................................................................................... 8
Figura 5 - prisma ........................................................................................................................... 8

7. Figura 19 ..................................................................................................................................... 28
Figura 20 ..................................................................................................................................... 28
Figura 21 ..................................................................................................................................... 28
Figura 22 ..................................................................................................................................... 29
Figura 23 ..................................................................................................................................... 29
V

8. 6
CAP. 1 – INTRODUÇÃO
A Topografia (lugar + descrição) era tradicionalmente a disciplina que se ocupava da arte de
representar minuciosamente o terreno localmente. Ao restringir essa representação a um
determinado local, pretendia-se simplificar os problemas de representação causados pela
curvatura das superfícies de nível.
Actualmente, devido ao interesse e necessidade de ter essas várias representações locais
interligadas de forma compatível e contínua, a representação topográfica do terreno já não
pode ser local nem pode ignorar a curvatura das superfícies de nível.
A essas representações chama-se Cartas ou Plantas Topográficas.
Esta representação da superfície da Terra em cartas ou mapas necessita que hajam pontos
posicionados sobre a sua superfície, mas também precisa de utilizar um método que permita
representar uma superfície que é curva sobre um plano. Para se conseguir fazer esta
representação plana da Terra têm que se fazer algumas escolhas:
- A escolha de um modelo para a forma do planeta;
A Terra, embora aparentemente redonda, tem uma forma geométrica muito complexa, e para a
representar num plano, necessitamos de ter uma superfície de referência, que se aproxime o
mais da realidade e ao mesmo tempo tenha uma definição matemática rigorosa e simples.
O Geóide;
A superfície terrestre definida pela superfície do nível médio das águas do mar e que
supostamente prolongada por baixo dos continentes é o denominado Géoide. É uma superfície
de referência bastante irregular não definida matematicamente cujo estudo é feito pela
geodesia.
O Elipsóide;
Como o Geóide é muito complexo, é usual utilizar-se como superfície de referência, um
elipsóide de revolução. Não existe, no entanto, apenas um elipsóide de referência, pois têm
sido vários os estudiosos a fazer uma aproximação à superfície terrestre e assim existem
vários elipsóides de revolução (temos, entre outros, os elipsóides de Bessel, Clarke, Hayford,
GRS80 e o WGS-84º). Por esta razão, e consoante a região que queremos representar terá
que se ter em conta qual o elipsóide com a melhor aproximação à superfície terrestre nessa
mesma região.
- A escolha de um sistema de coordenadas que permitam posicionar os pontos sobre a sua
superfície;
Para esse posicionamento utilizam-se vários sistemas, entre os quais:
Coordenadas Rectangulares (em Meridianas e Perpendiculares)
Coordenadas Geográficas (em Latitude e Longitude)
Figura 1 – elipsóide e geóide

9. 7
É de salientar que o conjunto de parâmetros que constituem a referência de um determinado
sistema de coordenadas geográficas ou altimétricas, se designam de Datum (ou Data no
plural).
Poderá ser um Datum Geodésico, no caso de se tratar de coordenadas geográficas ou um
Datum Altimétrico, no caso de se tratar de coordenadas altimétricas. A cada Datum está
associado um elipsóide de referência.
Existem dois tipos de data geodésicos:
Datum local;
O elipsóide é posicionado numa determinada área de interesse, de modo a minimizar a
diferença entre as coordenadas do geóide e do elipsóide.
Datum global;
O elipsóide é escolhido de modo a que o seu centro geométrico esteja centrado o mais próximo
possível com o centro de massa da Terra.
Alguns Data geodésicos utilizados em Portugal:
Designação Elipsóide associado Ponto de fixação
Datum Lisboa Hayford Castelo de S. Jorge
Datum 73 Hayford Melriça
Datum Europeu ED50 Hayford Potsdam, Alemanha
WGS84 Hayford Não tem pois é um Datum global
Tabela 1 - data geodésicos
– A escolha de um sistema de projecção cartográfica que permita fazer a sua representação
num plano;
As projecções cartográficas consistem na transformação das coordenadas geográficas em
rectangulares;
Existem vários modelos de projecções cartográficas:
Projecção azimutal;
Projecção cilíndrica (por exemplo: Mercator, Gauss-Kruger);
Projecção cónica (por exemplo: Bonne).
Ao conjunto destas escolhas, corresponde um Sistema de Projecção Cartográfica.
- Rede geodésica
Os levantamentos topográficos são, por norma, apoiados numa série de pontos com
coordenadas conhecidas, pontos esses que estão fisicamente no terreno, de forma facilmente
visível, designados por Vértices Geodésicos.
Ao conjunto destes vértices geodésicos (que criam uma malha triangular) chama-se Rede
Geodésica.
Estamos agora em condições de dizer que, este trabalho foi apoiado na Rede Geodésica
Nacional, e:
O levantamento foi efectuado no sistema Hayford-Gauss, Datum 73
A origem altimétrica tomada foi o Datum Altimétrico Nacional (Cascais)

10. 8
CAP. 2 – ADENSAMENTO (Irradiação)
2.1 – Objectivos
Neste trabalho, foram-nos fornecidos 2 pontos de coordenadas conhecidas (E2 e E3),
pertencentes à rede de apoio topográfico, e o nosso objectivo era determinar as coordenadas
de um ou mais novos pontos, numa localização que nos fosse útil no futuro (Cap. 3). Existem
vários métodos para determinar as coordenadas de novos pontos;
Irradiação
Triangulação
Poligonação
Intersecções
A este processo de obter novos pontos coordenados para juntar à rede, chama-se
adensamento topográfico.
Para efectuar qualquer um destes métodos necessitamos dos seguintes instrumentos de
trabalho;
- Estação Total
- Tripés
- Prisma (bastão)
- Fita métrica
- Nível Digital/ óptico
- Mira Topográfica.
A Estação Total é composta por teodolito e distanciómetro electrónico, permite medir ângulos
horizontais, verticais e obter distâncias. A estação total está apoiada no tripé de forma a ficar
nivelada.
O Prisma tem como funcionalidade receber um raio laser emitido pela estação total. Desta
forma a estação calcula a distancia para o ponto onde está situado o prisma.
Figura 2 - tripé Figura 3 - estação total
Figura 4 - bastão Figura 5 - prisma

11. 9
2.2 – Procedimentos e Cálculos
Ao irmos para campo a nossa primeira tarefa foi estacionar a estação total, o que fizemos
várias vezes ao longo das aulas de campo, por esse motivo, vamos agora explicar em detalhe
todos os passos, posteriormente não iremos discriminar todo este processo novamente, apesar
de o termos feito sempre com todo o rigor;
1. Ajustamos as pernas do tripé de forma a garantir que a estação total fique estável;
2. Nivelamos a superfície do tripé como mostra a figura 6;
3. Verificamos se o ponto topográfico está localizado diretamente abaixo do centro do
tripé;
4. Verificamos se a base do tripé está horizontal;
5. Pressionamos as pernas do tripé contra o solo
como mostra a figura 7;
6. Colocamos a estação total sobre o tripé, inserindo o parafuso do tripé na base da
estação e rodamos de forma a que a estação total fique fixa;
De seguida nivelamos a estação;
1. Movemos as pernas do tripé, utilizando os parafusos existentes nas pernas, para desta
forma calar a bolha de nível;
2. Rodamos os parafusos nivelantes até o nível electrónico estar centrado. Para tal a
bolha de nível electrónico tem obrigatoriamente que aparecer centrada no visor da
estação total como mostra a figura 8.
Figura 6 - nivelamento do tripé
Figura 7 - fixação das pernas do
tripé
Figura 8 - visor da estação

12. 10
Após este trabalho estacionámos em E3, e fizeram-se as seguintes leituras:
Tabela 2 - leituras do adensamento
Ao fazermos os primeiros cálculos, notámos que deveria haver algum erro, pois o que
estávamos a obter era diferente daquilo que constava no nosso croqui. Os pontos estavam a
ter coordenadas de certa forma simétricas ao que deveríamos obter. Ao falar com o professor
chegamos a conclusão que o aparelho estava a contar os ângulos no sentido anti-horário, em
vez do sentido horário. Bastou então fazer essa correcção às nossas leituras corrigidas;
400 −
e
400 −
Antes disso, porém fizemos as correcções às nossas leituras, pois fizemos leituras directas e
inversas (após a 1º leitura – leitura direta, rodou-se a Alidade 200g na horizontal e basculou-se
a luneta 200g na vertical, voltando nesta forma a fazer uma nova leitura – leitura inversa).
Essas correcções foram feitas da seguinte forma:
Para as leituras Azimutais;
=
+ 200
2
Em que será:
+200 < 200
e
−200 > 200
Para as leituras Zenitais;
=
+ (400 − )
2
– Leituras corrigidas
– Leituras directas
– Leitura inversa
– Leituras corrigidas
– Leituras directas
– Leitura inversa

13. 11
Uma vez que fizemos também leituras directas e inversas para as distâncias, através de uma
média aritmética simples, também as corrigimos.
∑
Então, o nosso quadro de leituras corrigidas é o seguinte:
Tabela 3 - leituras corrigidas do adensamento
NOTA: daqui em diante, sempre que foi necessário corrigir leituras utilizámos este método,
logo não voltaremos a fazer referência ao mesmo.
Após estes cálculos, e tendo conhecimento das coordenadas planimétricas de E2 e E3:
Estação Meridianas (m) Perpendiculares (m)
E2 -58.939,92 7.391,96
E3 -58.996,89 7.454,72
Tabela 4 - coordenadas planimétricas dos pontos conhecidos
Procedemos aos seguintes cálculos:
1 – Uma vez que eram conhecidas as coordenadas de E2 e E3, calculou-se o rumo (ângulo
que o Norte cartográfico faz com a direcção de E3 para E2) de E3 para E2, através da seguinte
fórmula:
( 3 2) =
∑ - somatório de todas as distâncias lidas
- número de leituras feitas
( 3 2) – rumo de E3 para E2
– meridiana do ponto E2
– meridiana do ponto E3
– perpendicular do ponto E2
– perpendicular do ponto E3
Figura 9 - rumo de E3 para E2

14. 12
Obtemos o seguinte:
( 3 2) =
−58938,92 + 58996,89
7391,96 − 7454,72
⇔ ( 3 2) =
−58938,92 + 58996,89
7391,96 − 7454,72
Nesta etapa, temos que ter em atenção este resultado, pois sabemos que consoante a posição
do ponto nos 1º, 2º, 3º ou 4º Quadrante, vamos ter que fazer um acerto ao resultado daquela
conta, então seguimos a seguinte tabela:
Quadrante Ajuste no resultado final
1º Q + 0g
2ºQ + 200g
3ºQ + 200g
4ºQ + 400g
Tabela 5 - quadrantes (para acertos no cálculos dos rumos)
Ou seja:
⇔ ( 3 2) = 46,9238 + 200; pois o ponto está no 2º Quadrante
NOTA: daqui em diante, sempre que foi necessário calcular
rumos por esta fórmula utilizámos este método, logo não
voltaremos a fazer referência ao mesmo.
2 – Uma vez que na leitura de E3 para E2, colocámos a
contagem dos ângulos azimutais a zeros, quer dizer que foi a
partir dessa direcção que o teodolito começou a ler os ângulos
horizontais.
Temos que o nosso rumo (E3 E2) é igual ao nosso R0 (ângulo
que o norte cartográfico faz com o zero do teodolito), figura 10.
3 – Como sabemos o rumo (E3 E2), podemos calcular o Rumo (E3 A), através da seguinte
forma:
( 3 ) = +
Onde;
- Leitura Azimutal corrigida de E3 para A
= ( 3 2)
Logo;
( 3 ) = ( 3 2) +
Neste momento, já sabemos o rumo (E3 A), estamos em condições de calcular as
coordenadas planimétricas do ponto A, através da fórmula do transporte de coordenadas:
Figura 10 - (E3 E2) é igual
ao R0

15. 13
= + 3 × ( 3 )
= + 3 × ( 3 )
Assim, concluiu-se o processo de adensamento (consultar croqui no anexo nº1), através do
método da irradiação, ficando a conhecer-se as coordenadas planimétricas deste novo ponto
A.
Nota: Este processo foi repetido (passos 1, 2 e 3), mas desta feita partindo de A, coordenando
com E3 e criando um novo ponto B, descobrindo as suas coordenadas. É a partir destes dois
novos pontos (A e B) que o Capitulo 3 tem o seu início.
Para uma melhor visualização do posicionamento dos pontos está no anexo nº 2 uma foto
aérea com a localização dos pontos.
2.3 – Conclusão
Em suma todo o processo do adensamento em campo decorreu normalmente, apesar da
nossa, ainda, pouca experiencia no manuseamento dos equipamentos. Só em gabinete na
elaboração dos cálculos é que detectámos que o nosso aparelho estava a ler no sentido
errado, o que conseguimos remediar sem voltarmos a campo como explicamos no
procedimento.
CAP 3 – LEVANTAMENTO TOPOGRÁFICO CLÁSSICO
3.1 – Objetivos
O levantamento topográfico consiste na obtenção – planimétrica e/ou altimétrica de pontos
existentes no terreno para posteriormente calcular as suas coordenadas e representa-los numa
carta ou planta.
Para a obtenção destes pontos é necessário proceder a um conjunto de operações.
Existem vários métodos de levantamentos topográficos:
- Métodos Clássicos da Topografia – Baseia-se na medição de ângulos e distâncias,
recorrendo a teodolitos, estações totais e níveis;
- Métodos Fotogramétricos – A informação é obtida através de fotografias aéreas
métricas ou imagens numéricas recolhidas por sensores instalados em satélites artificiais da
Terra;
- Sistema de Posicionamento Global (GPS) – Permite a determinação precisa das
coordenadas de locais onde são colocadas as antenas dos recetores;
- Sistemas de Varrimento Laser – Adquire coordenadas cartesianas tridimensionais,
recorrendo à tecnologia laser.
Foi nos proposto efectuarmos o levantamento topográfico da zona pedonal (passeios) situada
entre o bloco D e o bloco A (projeto 5), incluindo a zona da cancela localizada a saída do

16. 14
parque de estacionamento dos docentes, para o qual utilizamos o método clássico da
topografia.
3.2 – Procedimentos e Cálculos
Estacionamos a estação total no nosso ponto B, que obtivemos através do adensamento, como
já foi referido no capítulo nº2. Fizemos pontaria ao ponto A e colocamos a máquina a zero,
desta forma reunimos todas as condições para iniciarmos o levantamento topográfico.
Colocamos, o prisma em 54 pontos fazendo pontaria em cada um deles, em todos estes
pontos fizemos leituras dos Ângulos Azimutais (HZ - horizontais), Ângulos Zenitais (V –
verticais) e das distâncias da estação ao respetivo ponto, organizamos estes valores na tabela
que está no anexo nº3.
Com os valores obtidos calculamos as meridianas, perpendiculares e cotas para cada ponto.
Apos esse cálculo podemos elaborar o projecto em suporte digital do levantamento topográfico,
que pela sua dimensão não foi possível fazer a saída gráfica num formato A4 mas sim num A3
para assim manter a escala 1/500 que está no Anexo nº4.
Para obtermos valores das meridianas e perpendiculares, utilizamos a fórmula do transporte de
coordenadas, para tal será necessário calcular o rumo (BA);
( ) = +
Rumo (AB) 46,3970g
MA -58998,99m
PA 7571,62m
MB -58954,73m
PB 7621,20m
Tabela 6 - dados (para levantamento)
Rumo (BA);
Conhecendo de antemão o rumo (AB) calculado no capitulo anterior;
( ) = ( ) + 200
( ) = 46,3970 + 200
( ) = 246,3970
De seguida calcula-se o R0, uma vez que colocamos o zero da máquina de B para A, o rumo
(BA)=R0. Depois, com o R0, sabemos que os rumos dos pontos todos seguintes são feitos da
seguinte forma:
( 1) = + ⇔ ( 1) = ( ) +
Depois de saber o valor do rumo (B1), podemos calcular o valor das meridianas e
perpendiculares, através das seguintes fórmulas:

17. 15
= + 1 × ( 1)
Meridianas;
– meridiana de 1 (incógnita)
– meridiana do ponto B (conhecida)
1 – distancia do ponto B para o ponto 1
( 1) - rumo de B para 1
Exemplificamos aqui um cálculo de meridianas para o ponto 1;
M = −58,954 + 72,172 × Sen(245,4634)
M = −59002,00
Perpendiculares;
= + 1 × ( 1)
– perpendicular de 1 (Incógnita)
– perpendicular do ponto B (conhecida)
1 – distancia do ponto B para o ponto 1
( 1) – rumo de B para 1
Exemplificamos aqui um calculo de perpendiculares para o ponto 1;
= 7621,20 + 72,172 × (245,4634)
= 7566,66
Para calcular as cotas utilizamos a fórmula de cálculo de coordenadas altimétricas;
= 1 × ( ) + − +
– cota do ponto 1 (incógnita)
1 - distância do ponto B para o ponto 1
- leitura zenital de B para 1
- altura da estação total
- altura do bastão
– cota do ponto B (conhecida)
Exemplificamos aqui um cálculo de cotas para o ponto 1;
= 1 × + − + ⇔ = 72,172 × (98,0175) + 1,47 − 2 + 56,03 ⇔
⇔ = 57,75
Todos os cálculos das Meridianas, Perpendiculares e Cotas para os 54 pontos foram
efectuados em Excel (anexo nº3).

18. 16
3.3 – Conclusões
O nosso trabalho de levantamento em comparação com os outros trabalhos que fizemos foi o
que se revelou mais sistemático, tanto no terreno como em gabinete. Foi também o trabalho
em que tivemos de recorrer ao autocad, programa que praticamente desconhecíamos tornando
assim a representação gráfica do levantamento um processo bastante trabalhoso.
CAP. 4 – NIVELAMENTO GEOMÉTRICO
4.1 – Objectivos
Este procedimento, pertence à vertente altimétrica da topografia. Esta operação de
nivelamento, serve no fundo para determinar a diferença de nível entre dois pontos.
Para tal procedimento utilizamos um nível ótico;
O Nível ótico, define com grande precisão linhas de visada horizontal. Á semelhança dos
teodolitos ou estações totais são formados por uma base e uma alidade, que roda em torno do
eixo principal.
Desta forma, para conseguirmos uma boa montagem do aparelho, temos que respeitar de
forma rigorosa que o eixo principal esteja vertical.
Existem vários tipos de nivelamento;
- Nivelamento Geométrico:
É o mais exacto dos três e obtém-se fazendo visadas horizontais a partir do Nível, para uma
régua aferida (figura 12), chamada de Mira Topográfica. Para distâncias superiores a 500m,
temos que ter em atenção a influência da forma da Terra e da refracção atmosférica.
Figura 11 – nível ótico Figura 12 - régua

19. 17
Nos casos em que a distância é grande ou não há visibilidade entre dois pontos, pode haver
necessidade de criar mais estações de nivelamento, conforme a figura 14, é chamado de
Nivelamento Composto.
Nivelamento Trigonométrico:
É feito a partir de um Teodolito com visadas com qualquer inclinação, é mais rápido que o
Geométrico.
- Nivelamento Barométrico:
É feito a partir do relacionamento da pressão atmosférica e a altitude. Tem um maior erro
associado, mas dispensa a visibilidade entre os pontos.
Neste nosso trabalho, utilizámos o Nivelamento Geométrico, onde, partimos de um ponto de
coordenadas conhecidas (E3) e fizemos um nivelamento composto, partindo de E3 para B
passando por A (pontos materializados no terreno, consequência do Capítulo 2) e um contra
nivelamento (passando igualmente por A, mas no sentido, B para E3), obtendo assim as
coordenadas altimétricas intermédias dos pontos A e B, (verificando assim as coordenadas
altimétricas dos pontos obtidos no Capítulo anterior).
Figura 13 - nivelamento geométrico
Figura 14 - nivelamento composto

20. 18
4.2 – Procedimentos e Cálculos
Estacionamos, numa posição intermédia entre o ponto E3 e o ponto A, para assim fazermos
leituras atrás (para E3) e leituras à frente (para A), depois e mantendo a mira em A
estacionámos numa nova posição intermédia entre A e B, voltando a repetir o procedimento
anterior, mas agora a leitura atrás foi para A e a leitura à frente foi para B. Mantendo este
procedimento, fizemos então o contra nivelamento, como mostra a figura 15.
Nota: As leituras que retiramos foram sempre a leitura media e a leitura superior.
E desta forma obtivemos as seguintes leituras:
Pontos
Visados
Niveladas
Atrás (m) À frente (m)
E3
1.890
1.725
----
A
1.178 1.939
1.052 1.615
---- ----
B
2.784 2.900
2.569 2.681
---- ----
A
1.972 1.053
1.700 0.938
---- ----
Tabela 7 - leituras do nivelamento
A partir destes valores sabemos que:
= á −
Ou seja, a diferença de nível entre 2 pontos é-nos dada pela diferença entre a leitura atrás e a
leitura à frente.
Figura 15 - nivelamento e contra nivelamento

21. 19
Como se trata de um nivelamento, com contra nivelamento, e onde, supostamente a única
coordenada conhecida é a do ponto E3, ao partir de uma determinada cota (a de E3), e
somando todos os desníveis seguintes (com atenção para manter sempre o mesmo sentido de
percurso e sequência de leituras), deveríamos chegar novamente ao valor da cota do ponto E3.
Acontece que, por norma isto não acontece, porque temos um erro associado (erro de fecho).
Vamos então de ter que distribuir esse erro de forma equitativa, pelo número de niveladas que
fizemos, e aí sim temos que chegar novamente ao valor da cota do ponto de partida.
De seguida apresentámos a tabela 8 que utilizámos para exibir este cálculo:
PONTOS NIVELADAS
DESNÍVEIS
OBSERVADOS CORREÇÕES
DESNÍVEIS
COMPENSADOS
COTAS
VISADOS ATRÁS
À
FRENTE
"+ "
"-"
"+ "
"-"
Tabela 8 - nivelamento geométrico
Este tipo de quadro (ou método de cálculo), permite-nos fazer várias verificações ao longo do
processo, ou seja:
Na 2ª e 3ª coluna temos as leituras feitas atrás e à frente (apenas as leituras médias foram
consideradas para este cálculo).
Ao fazer o somatório das leituras atrás e subtraindo o somatório das leituras à frente,
Σ á − Σ
Obtemos um valor que é o desnível entre E3 e E3 ( ), calculado na última coluna da
Tabela 8
Nas colunas 4 e 5 da Tabela 8, representamos os desníveis entre cada ponto e colocamos
esse valor na coluna 4 se o valor for positivo, e/ou colocamos esse valor na coluna 5 se o
mesmo for negativo.
O somatório de cada coluna é feito e representado na última linha da coluna respectiva.
Ao somatório dos desníveis da coluna 4 subtraímos o somatório dos desníveis da coluna 5.
Este resultado tem que ser igual ao encontrado anteriormente, na conta:
Σ á − Σ
(Ao fazer isto estamos a fazer a nossa primeira verificação de cálculos).

22. 20
De seguida, ao valor obtido na ultima linha da coluna três (que como vimos tem que ser igual
ao da coluna cinco) subtraímos o valor da ultima linha da coluna nove (diferença de nível entre
o ponto de partida e o ponto de chegada), o resultado tem que ser zero.
Como isso não acontece, vamos ter que encontrar o erro de fecho, que se traduz no seguinte
cálculo:
= Σ − Σ −
Logo, o nosso erro de fecho foi igual a -0,026
m
.
Agora, temos que distribuir este erro pelo número de niveladas que efectuamos, ou seja:
=
−
Onde, c é a correcção e n corresponde ao número de niveladas, que neste caso foram 4.
Temos que ter em atenção pois, se estamos a trabalhar com um número 3 casas decimais nas
leituras a correcção terá de ser feita de forma a manter essas 3 casas decimais.
Ou seja,
=
−(−0,026)
4
= 0,0065
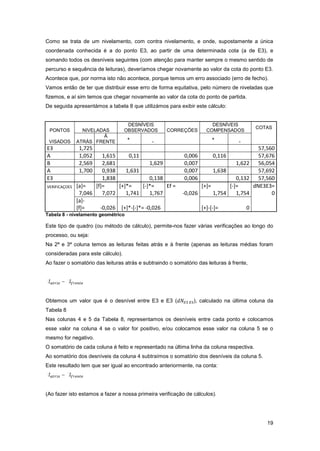
Então a compensação a cada desnível foi feito conforme está a 6ª coluna da Tabela 8,
compensando os desníveis maiores com um valor um pouco maior também e mantendo as 3
casas decimais.
Nas colunas 7 e 8 somamos ou subtraímos, conforme a situação, o valor da compensação ao
respectivo desnível, e a isto chamamos – Compensação angular.
Se ao somatório de desníveis compensados positivos, subtrairmos o somatório dos desníveis
compensados negativos, temos que obter um valor igual à diferença de nível entre E3 e E3.
Ou seja,
Σ[+] − Σ[−] =
(E aqui estamos a fazer uma segunda verificação dos cálculos);
Por fim, basta a partir do valor da cota do ponto E3, ir somando ou subtraindo os valores
encontrados dos desníveis compensados chegando novamente, e obrigatoriamente ao valor da
cota de E3 (última verificação).
Com isto encontramos os valores das cotas compensadas de A e de B, ou seja cotas
intermédias entre o ponto de partida e o ponto de chegada.

23. 21
4.3 – Conclusões
Como podemos verificar pela Tabela 8 temos um valor de cota para A de 57,676
m
no
nivelamento e temos um valor de 57,692m no contra-nivelamento.
Ou seja, obtivemos uma diferença de 0.016m, quando deveriam ser iguais.
Esta diferença leva-nos a crer que deverá ter havido algum tipo de erro ao nível de:
- Leituras na mira
Uma vez que foi a primeira vez que o fizemos, e em muitos casos temos que calcular um valor
aproximado, pois a escala da mira não é tão pequena como gostaríamos.
- A escolha da colocação do nível
Pois temos conhecimento que para maior rigor, o nível deverá ser colocado sensivelmente a
igual distância das leituras a fazer, bem como o ideal será depois manter, aproximadamente
essas distâncias nos próximos nivelamentos.
Como podemos verificar pela figura 16, temos umas distâncias entre visadas pouco equitativas
– sendo que para obtermos estas distâncias é que utilizámos as leituras superiores, da Tabela
7, em que a distância D foi obtida pela seguinte fórmula:
= ( )
Onde,
= ( − é ) 2 ( )
= 100 = é
- Montagem do aparelho
Pode o aparelho não ter ficado perfeitamente verticalizado, causando,
consequentemente, erros.
Apesar deste erro, temos noção de que fomos bastante rigorosos com os procedimentos de
nivelamento, o que nos leva a concluir, mais uma vez, que é um processo que carece de
Figura 16 - distancias do nivelamento

24. 22
grande rigor em todos os seus passos, pois os resultados, como pudemos ver, são
influenciados por isso.
CAP. 5 – TRIANGULAÇÃO
5.1 – Objectivo
Em topografia o que determina um bom trabalho é a precisão com que é feito, a
triangulação tem como objectivo a determinação das coordenadas de um ponto de forma
bastante exacta, conhecendo outros dois pontos. Era nosso objectivo criar um novo ponto no
cruzamento dos passeios do bloco D e da Biblioteca, utilizando os pontos conhecidos E3 e E4.
5.2 – Justificação dos cálculos
Neste procedimento, estacionamos em todos os pontos, E3, E4 e no novo ponto P,
onde retiramos leituras Azimutais directas e inversas em todos os pontos, após a correcção
das leituras determinamos os três ângulos internos. Ao calcular os ângulos internos
compensamos esses ângulos distribuindo o erro equitativamente pelos três ângulos. Desta
forma ficamos em condições de obter todas as distâncias do triângulo que é formado pelos três
pontos, através da lei dos senos. Após a resolução do triângulo avançámos para o cálculo das
coordenadas planimétricas do novo ponto P, que foram calculadas utilizando os pontos
conhecidos.
Para calcular as coordenadas planimétricas do novo ponto em primeiro lugar retiramos de
campo as leituras já referidas cujos valores foram colocados em três tabelas que dizem
respeito a cada um dos três pontos em que estacionamos, para uma melhor organização foram
colocadas as leituras corrigidas nas mesmas tabelas;
L directa L indirecta L corrigida
P E3 125,9303
g
325,9316
g
125,9310
g
P E4 182,787
g
382,7898
g
182,7884
g
Tabela 9 – leitura de P
L directa L indirecta L corrigida
E3 P 105,7050
g
305,6997
g
105,7024
g
E3 E4 3,2575
g
203,2576
g
3,2576
g
Tabela 10 – leitura de E3
L directa L indirecta L corrigida
E4 P 25,7649
g
225,7649
g
25,7646
g
E4 E3 66,4760
g
266,4615
g
66,4688
g
Tabela 11 – leitura de E4

25. 23
Para a determinação dos ângulos internos do triângulo subtraímos á leitura do ponto que fica á
direita a leitura do ponto que fica á esquerda, no caso do ponto P obtemos as seguintes leituras
(esquematizado na figura 17);
De seguida efectuamos o seguinte cálculo;
P*= 182,7884-125,9310= 56,8574
g
Nos outros pontos utilizamos o mesmo método;
Ê3*= 105,7024-3,2576= 102,4448
g
Ê4*= 66,4688-25,7646= 40,7042
g
Para determinar o erro de fecho somámos os três ângulos internos o que nos deu diferente de
200,0000g, essa diferença é o nosso ƒ;
ƒ= P*+Ê3*+Ê4*= 56,8574+102,4448+40,7042= 200,0064-200,0000= 0,0064
ƒ
3
=
0,0064
3
= 0,0021 + 0,0021 + 0,0022
Para calcular os ângulos compensados subtraímos o erro ao ângulo inicial;
P= 56,8574-0,0021= 56,8553g
Ê3= 102,4448-0,0022= 102,4426g
Ê4= 40,7042-0,0021= 40,7021g
P+Ê3+Ê4= 200,0000g
Nesta fase para calcularmos as coordenadas só nos faltavam as distâncias de E3 para P e de
E4 para P e os rumos E3 para P e E4 para P. Obtivemos a distância de E3 para E4 pelas suas
coordenadas já conhecidas;
3 4 = ∆ − ∆ = (−59041,69 + 58996,89) + (7532,27 − 7454,72) = 89,5603
E com esta obtivemos as que nos faltavam pela lei dos senos;
Figura 17 - leituras a partir de P (triangulação)

26. 24
3
(Ê4)
=
3 4
( )
⇔
3
(40,7021)
=
89,5603
(56,8553)
⇔ 3= 68,5977
4
(Ê3)
=
3 4
( )
⇔
4
(102,4426)
=
89,5603
(56,8553)
⇔ 4= 114,8826
Nesta fase temos o triangulo resolvido como mostra a figura 18;
Para calcular o rumo E3 para E4 utilizamos as coordenadas já conhecidas dos dois pontos;
( 3 4) =
∆
∆
=
−59041,69 + 58996,89
7532,27 − 7454,72
=
−44,8
77,55
= −33,3496 + 400
= 366,6504
Após termos este rumo com os ângulos internos calculamos os restantes;
( 3 ) = ( 3 4) + Ê3 = 366,6504 + 102,4426 = 69,0930
( 4 3) = ( 3 4) − 200 = 366,6504 − 200 = 166,6504
( 4 ) = ( 4 3) − Ê4 = 166,6504 − 40,7021= 125,9483
Nesta fase para calcular as coordenadas basta substituir, este calculo foi feito através de E3 e
E4;
Por E3:
= + 3 × ( 3 ) ⇔ = −58996,89 + 68,5977 × (69,093) ⇔
= −58936,22
= + 3 × ( 3 ) ⇔ = 7454,72 + 68,5977 × (69,093) ⇔ = 7486,73
Por E4:
= + 4 × ( 4 ) ⇔ = −59041,69 + 114,88 × (125,9483) ⇔
= −58936,22
= + 4 × ( 4 ) ⇔ = 7532,27 + 114,88 × (125,9483) ⇔ = 7486,73
Para uma apresentação de resultados mais clara apresentamos anexo nº5 a tabela da
triangulação.
Figura 18 - triangulo resolvido (triangulação)

27. 25
5.3 – Conclusão
Em suma podemos dizer que foi um trabalho que correu normalmente, obtemos um
erro de fecho angular dentro do aceitável. Demos bastante importância ao rigor nas diversas
fazes da triangulação, desde a montagem da estação ao calar bem a bolha de nível, na
colocação do bastão demos muita importância á sua verticalidade, e também na pontaria ao
prisma fomos o mais rigorosos possível. Sempre que possível fizemos pontaria ao “bico” do
bastão para maior rigor ao nível azimutal, deslocando posteriormente a luneta só na vertical
para fazer pontaria no prisma.
Cap. 6 – IMPLANTAÇÃO
6.1 – Objetivos
Tendo conhecimento das coordenadas de um ou mais pontos, o objectivo da
implantação é descobrir onde estão esses pontos no terreno e materializá-los (normalmente
com a colocação de estacas). Para o fazer necessitamos de partir de 2 pontos conhecidos. No
nosso caso os pontos conhecidos são o E3 e P, através destes dois pontos vamos implantar os
pontos P1, P2, P3 e P4.
6.2 – Procedimentos e Cálculos
Assumimos como ponto de partida para a marcação dos pontos 1, 2, 3 e 4 o ponto P,
que vem da triangulação (capitulo 5), a partir desse ponto tivemos que calcular os ângulos que
teremos que ler no aparelho quando estamos na direcção do ponto pretendido. Para isso
forçamos a zero para E3 e temos:
= ( 3) = ( 3 ) + 200 = 69,0952 + 200 = 269,952
Após a marcação a zero ficamos com o R0 igual ao rumo de P para E3.
Para obter a leitura de P para o ponto 1 é necessário ainda calcular o rumo de P para 1;
( 1) =
∆
∆
( 1) =
−58941,12 + 58936,22
7485,51 − 7486,73
=
−4,9
−1,22
= 84,4653 + 200 = 284,4653
Estamos assim em condições de calcular a leitura de P para 1 através da formula seguinte;
( 1) = + ⇔ ( 1) = + ( 3) ⇔ = ( 1) − ( 3)
= ( 1) − ( 3) = 284,4653 − 269,0952 = 15,3701
Utilizamos a mesma ordem de ideias para calcular a leitura e P para os pontos 2, 3 e 4:
( 2) =
∆
∆
( 2) =
−58937,33 + 58936,22
7485,82 − 7486,73
=
−1,11
−0,91
= 56,2827 + 200 = 256,2827
= ( 2) − ( 3) = 256,2827 − 269,0952 = −12,8125 + 400 = 387,1875

28. 26
( 3) =
∆
∆
( 3) =
−58937,44 + 58936,22
7483,22 − 7486,73
=
−1,22
−3,51
= 21,2959 + 200 = 221,2959
= ( 3) − ( 3) = 221,2959 − 269,0952 = −47,7993 + 400 = 352,2007
( 4) =
∆
∆
( 4) =
−58939,91 + 58936,22
7483,38 − 7486,73
=
−3,69
−3,35
= 53,0722 + 200 = 253,0722
= ( 4) − ( 3) = 253,0722 − 269,0952 = −16,023 + 400 = 383,9770
Após termos as leituras (direcções) de todos os pontos falta-nos a distância dos pontos a
implantar ao nosso ponto de partida P, que calculamos relacionando as coordenadas
planimétricas do ponto P e dos pontos a implantar:
1 = (∆ ) + (∆ ) = (−58941,12 + 58936,22) + (7485,51 − 7486,73) = 5,0496
2 = (∆ ) + (∆ ) = (−58937,33 + 58936,22) + (7485,82 − 7486,73) = 1,4353
3 = (∆ ) + (∆ ) = (−58937,44 + 58936,22) + (7483,22 − 7486,73) = 3,7160
4 = (∆ ) + (∆ ) = (−58939,91 + 58936,22) + (7483,38 − 7486,73) = 4,9838
Os dados que levamos para campo foram os seguintes:
Pontos Leitura Azimutal (g) Distância ao ponto P (m)
1 15,3701 5,0496
2 387,1875 1,4353
3 352,2007 3,7160
4 383,9770 4,9838
Tabela 12 - dados para implantação
Após termos feito a implantação, tivemos de saber se havia necessidade de fazer aterro ou
escavação nos respectivos pontos;
Tabela 13 - calculo de aterro ou escavação

29. 27
Na última fase da implantação, quando descobrimos exactamente no terreno onde estava
materializado cada um dos pontos, e antes de cravar as estacas, registamos as leituras
zenitais, para cada um dos pontos.
NOTA: Não fizemos as leituras depois de colocar as estacas, pois ainda não sabíamos que era
suposto faze-lo. Apesar disso resolvemos tirar as medidas na mesma.
Recorde-se que iniciamos este processo (implantação), colocando o zero da estação para E3,
tirando também a leitura zenital e a distancia.
Dispomos assim dos seguintes dados:
Tabela 14 - dados da implantação
Vamos agora calcular as coordenadas altimétricas (cotas) reais, no terreno, de cada um dos
pontos P1, P2, P3 e P4, ou seja, na altura que fizemos as leituras.
Para isso fizemos os seguintes cálculos;
= 3 × ( ) + − ⇔ − = 3 × ( ) + −
Para utilizar esta fórmula só nos faltava calcular a distância de P para E3;
3 = Δ + ΔP ⇔ 3 = (−58996,89 + 58936,22) + (7454,72 − 7486,73) ⇔
⇔ 3 = 68,5966
Fica então;
57,56 − = 68,5966 × (99,8925) + 1,512 − 1,50 ⇔ 57,56 = + 0,1278 ⇔
⇔ = 57,43
Sabendo agora a cota de P vamos proceder exactamente da mesma forma com os restantes
pontos partindo, agora, da cota conhecida NP, para todos os outros pontos.
Ficamos então a conhecer as cotas reais dos pontos no terreno ás quais vamos adicionar o
valor da estaca, e depois ver a diferença entre a cota pretendida e a cota real à qual somamos
a altura da estaca. É este valor que:
- Se for negativo indica-nos o valor da escavação a fazer a partir do topo da estaca;
- Se for positivo indica-nos o valor do aterro a fazer a partir do topo da estaca.

30. 28
Tabela 15 - cálculo de escavação ou aterro
Temos então que fazer aterro, nas quantidades dos valores acima mencionados.
A implantação final ficou conforme a foto no anexo nº6.
No final da nossa operação de implantação, tivemos ainda uma pequena missão extra. Fazer,
através da estação total, uma visada para a base do edifício da biblioteca e uma para o topo,
registando apenas as leituras zenitais, e registar a distância horizontal até ao edifício. O sítio
onde estacionámos não era relevante. O objectivo era calcular a altura do edifício.
Dados recolhidos:
Leitura Zenital ao topo: 74,4657
g
Leitura Zenital à base: 103,3902
g
Distância: 26,724
m
O cálculo para a determinação da altura do edifício foi o seguinte:
NOTA: Aproveitando este cálculo, e utilizando um método bastante gráfico para demonstrar a
sua resolução, pretendemos com isso mostrar a importância que os croquis, esboços ou
qualquer outro tipo de representação gráfica auxiliar têm para ajudar a resolver alguns
problemas, ajudar na compreensão dos mesmos ou, por exemplo, servindo como auxiliar de
memória, para que o trabalho de gabinete subsequente ao trabalho de campo possa ser o mais
rigoroso e facilitado possível.
Continuando então com o cálculo, na figura 19, podemos facilmente observar que se à leitura
feita à base, subtrairmos a leitura feita ao topo, ficamos com o ângulo interno a sombreado,
que passamos a chamar de Ê.
Logo,
Ê = 103,3902
g
– 74,4657
g
= 28,9245
g
Por outro lado, se observarmos a figura 20, e sabendo que o teodolito faz o início da contagem
dos ângulos zenitais no seu eixo vertical (em cima) e esse eixo é perpendicular ao eixo
horizontal, que nos indica a distância ao edifício, sabemos também que o ângulo formado entre
eles é de 100
g
.
Logo,
Figura 20Figura 19 Figura 21

31. 29
A diferença entre a leitura à base e esses 100
g
, vai-nos dar o ângulo, que denominámos de ^B;
^B = 103,3902 – 100
g
= 3,3902
g
Da mesma forma, se ao ângulo de 100
g
subtrairmos a leitura ao topo do edifício – figura 21,
ficamos com o ângulo que designámos de ^T.
^T = 100
g
– 74,4657
g
= 25,5343
g
Agora, e recorrendo apenas a simples trigonometria, e separando o cálculo em duas partes,
observamos:
- Pela figura 22, vemos que ( ) =
. .
. .
⇔ ( ) = ⇔ = 11,33
- Pela figura 23, vemos que ( ) =
. .
. .
⇔ ( ) = ⇔ = 1,42
Consequentemente, a altura do edifício é:
Altura edifício = h1 + h2= 11,33 + 1,42 = 12,75
m
6.3 – Conclusões
Pode-se concluir que na implantação, temos que ter bastante desenvoltura no manuseamento
do aparelho para o trabalho decorrer com alguma fluidez. Será a partir deste momento que
nascerá a obra, é de extrema importância o rigor da implantação dos pontos.
Cap. 7 – Conclusões finais
Podemos dizer em termos gerais, que a topografia é uma área que está intimamente ligada à
engenharia civil, e foi, portanto, muito útil para nós, futuros engenheiros civis, ter esta noção do
funcionamento e amplitude da topografia.
Podemos dizer que é de extrema importância o rigor que um topógrafo tem que ter no decorrer
do seu trabalho, pois isso irá influenciar todo o trabalho que vem a seguir ao dele.
Ao mesmo tempo, o engenheiro civil que conheça, minimamente o que um topógrafo faz, e
pode fazer, também pode maximizar ou agilizar o seu próprio trabalho.
Além disso, não só ficámos com a noção de como interpretar informação topográfica, como
ficámos com conhecimentos relacionados com a Cartografia, Geodesia, Fotogrametria,
sistemas de posicionamento espacial (GPS) e métodos de nivelamento.
O balanço foi, portanto, positivo.
Figura 22
Figura 23

32. 30
Cap. 8 – Anexos
Nº1 Croqui do adensamento

33. 31
Nº2 Foto aérea com indicação dos pontos

34. 32
Nº3 Tabela do levantamento

35. 33
Nº4 Levantamento topográfico

36. 34
Nº5 Tabela de triangulação
Estações P E3 E4
P 125,9310g 182,7884g
E3 105,7024g 3,2576g
E4 25,7646g 66,4688g
Ângulos Ângulos Corrigidos
P* 56,8574g P 56,8553g
E3* 102,4448g E3 102,4426g
E4* 40,7042g E4 40,7021g
Σ = 200,0064g Σ = 200,0000g
Erro 0,0064g
Compensação
angular 0,0021+0,0021+0,0022
Estações M (metros) P (metros)
E3 -58996,89 7454,72
E4 -59041,69 7532,27
Rumo (g) (E3E4) Distância (m) 89,5603m
Resolução do triângulo
(m)
E3P 68,5977m
E4P 114,8826m
Cálculo de rumos (g)
E3P 69,0930g
E4P 125,9483g
Coordenadas ajustadas M (metros) P(metros)
Nova estação 1 (por E3) -58936,22 7486,73
Nova estação 2 (por E4) -58936,22 7486,73
Nº6 Foto da implantação

37. 35
Nº7 Trabalho em suporte digital (CD)

38. DECLARAÇÃO DE ORIGINALIDADE
Os autores deste trabalho declaram que o conteúdo do mesmo é da sua autoria e não constituí
cópia parcial ou integral de trabalhos de outro(s) autor(es).
(Assinaturas dos autores)
O não cumprimento está sujeito a sanção disciplinar conforme previsto no artigo 134º dos
Estatutos do IPL