O documento discute os principais conceitos da termoquímica, incluindo:
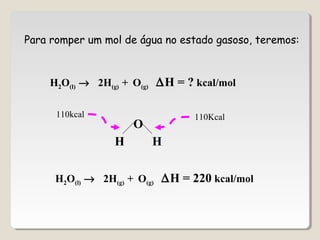
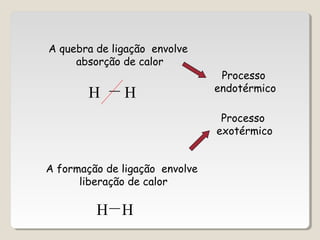
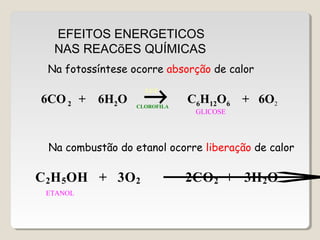
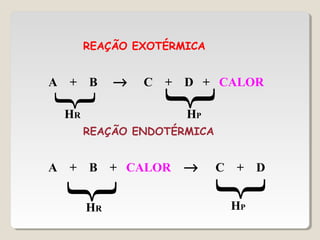
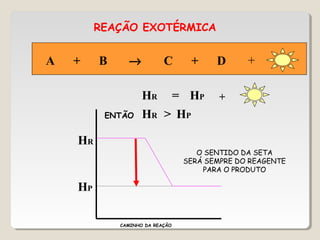
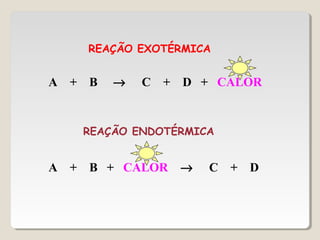
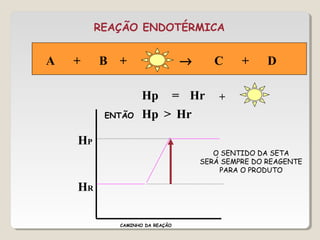
1) As reações químicas podem ser exotérmicas ou endotérmicas dependendo se liberam ou absorvem calor;
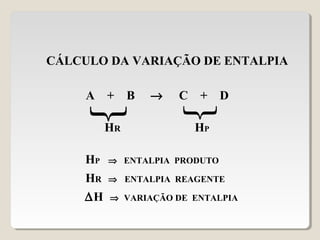
2) A variação de entalpia (ΔH) de uma reação pode ser calculada subtraindo a entalpia dos reagentes da entalpia dos produtos;
3) A lei de Hess permite calcular a variação de entalpia de uma reação através da soma das variações de entalp
















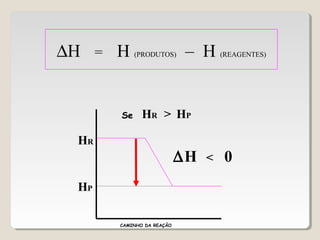
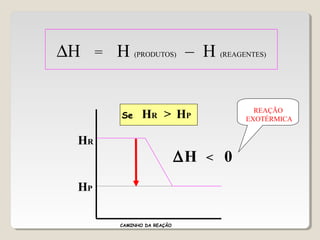
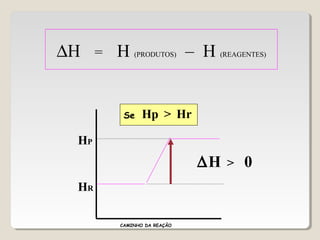
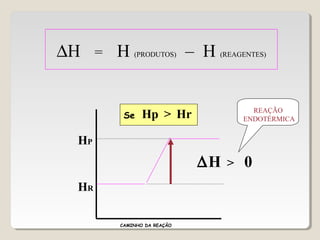




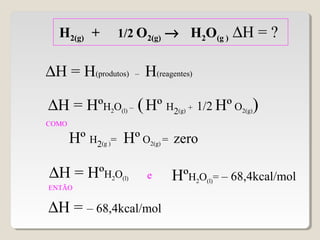
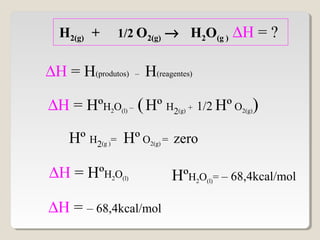
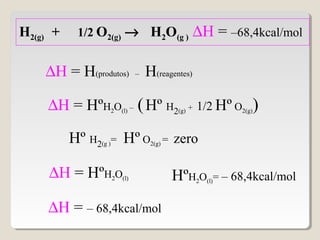
















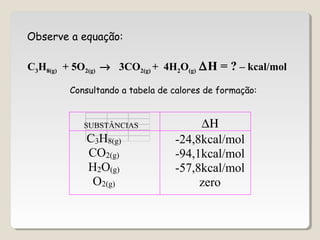
![∆H = ∑∆H(produtos) – ∑∆H(reagentes)
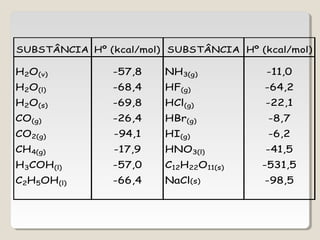
∆H = [ 3(-94,1) + 4(-57,8)] - (-24,8 + zero)
∆H = [3∆HCO2(g)+ 4∆HH2O(g) ] - (∆HC3H8(g)+5∆HO2(g) )
∆H = - 488,7 kcal/mol](https://image.slidesharecdn.com/termoquimica-101025131346-phpapp02/85/Termoquimica-1-e-2-54-320.jpg)