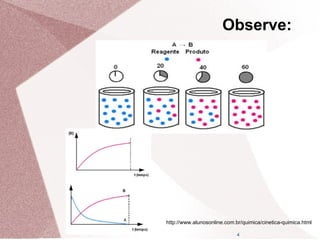
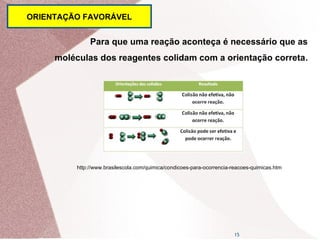
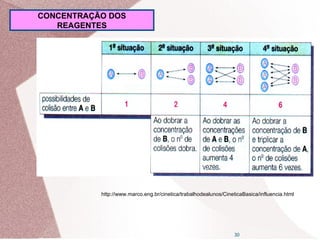
1. O documento discute cinética química e apresenta fatores que influenciam na velocidade das reações, como concentração dos reagentes, temperatura, catalisadores e inibidores.
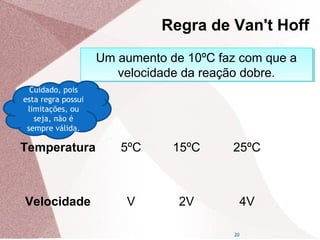
2. A cinética química estuda a velocidade das reações e os fatores que a influenciam. A velocidade de uma reação aumenta com o aumento da concentração dos reagentes e da temperatura.
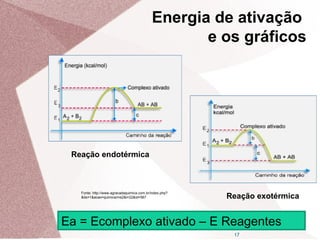
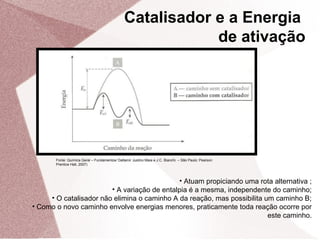
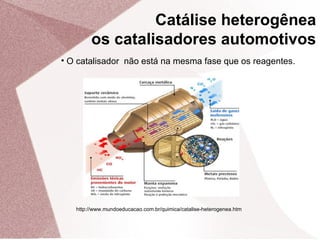
3. Catalisadores aumentam a velocidade das reações enquanto inibidores a diminuem, agindo sobre a energia de




![6
Velocidade média=−
Δ[ A]
Δt
=
Δ[B]
Δt
Para a reação:
A → B
Variação da quantidade de um reagente
ou produto em uma reação química num
intervalo de tempo.
vm=
Δm
Δt
ou
Δn
Δt
ou
ΔV
Δt
ou
ΔC
Δt
m = massa, n = no
mols, V = volume, C = concentração
molar
Velocidade média de um
componente da reação (Vm)](https://image.slidesharecdn.com/cineticaquimica-140629102500-phpapp02/85/Cinetica-quimica-6-320.jpg)
![7
Uma reação apresenta uma reação média que pode ser
obtida pela divisão da velocidade de cada componente da
reação química pelo respectivo coeficiente estequiométrico.
aA + bB → cC + dD
Vm = -∆[A]
a∆t
= --∆∆[B][B]
b∆t
=-∆[B] ∆[C]
c∆t
= ∆[D]
d∆t
Exemplo geral:
Velocidade média
da reação (Vm)](https://image.slidesharecdn.com/cineticaquimica-140629102500-phpapp02/85/Cinetica-quimica-7-320.jpg)
![8
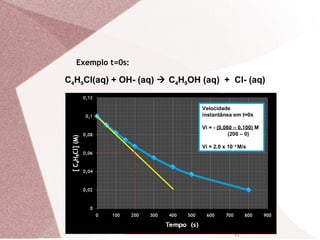
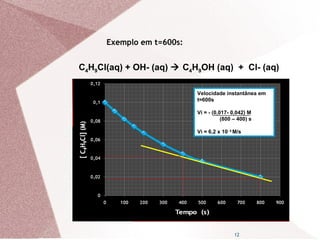
C4H9Cl(aq) + OH- (aq) C4H9OH (aq) + Cl- (aq)
Tempo
(s)
[C4H9Cl]
(M)
0 0,1000
50 0,0905
100 0,0820
150 0,0741
Comportamento
gráfico](https://image.slidesharecdn.com/cineticaquimica-140629102500-phpapp02/85/Cinetica-quimica-8-320.jpg)


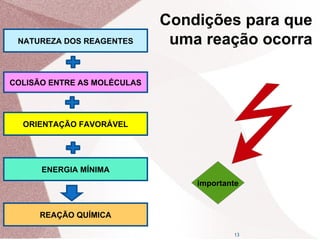







![Dado a REAÇÃO ELEMENTAR abaixo:
aA + bB cC + dD
V = K[A]a
. [B]b
A lei de velocidade será dada por::
a e b são os expoentes de A e B,
que correspondem aos coeficientes
estequiométricos da reação.
“ A velocidade de uma reação química
elementar, a uma dada temperatura, é
diretamente proporcional ao produto das
concentrações dos reagentes, em mol/L,
elevadas aos seus respectivos
coeficientes estequiométricos.”
“ A velocidade de uma reação química
elementar, a uma dada temperatura, é
diretamente proporcional ao produto das
concentrações dos reagentes, em mol/L,
elevadas aos seus respectivos
coeficientes estequiométricos.”
Fonte:
http://en.wikipedia.org/wiki/Cato_Maximilian_Guldberg
A lei de velocidade das reações (ou lei de
Guldberg –Waage) foi proposta em 1867
pelos cientistas noruegueses Cato
Maximilian Guldberg (1836-1902) e Peter
Waage (1833-1900)
Lei da velocidade
reação elementar](https://image.slidesharecdn.com/cineticaquimica-140629102500-phpapp02/85/Cinetica-quimica-32-320.jpg)

![REAÇÕES ELEMENTARES GERAIS
Exemplos Molecularidade Lei de Velocidade
A produtos Unimolecular V=K[A]
2A produtos Bimolecular V=K[A]2
A + B
produtos
Bimolecular V=K[A] [B]](https://image.slidesharecdn.com/cineticaquimica-140629102500-phpapp02/85/Cinetica-quimica-34-320.jpg)

![Reação genérica: 2A + 3B + C Produtos2A + 3B + C Produtos
Experimento [A]0(mol/L) Velocidade inicial da
reação (mol/L.min)
I 1 0,02
II 2 0,04
III 4 0,08
Lei das velocidades
Reação não elementar](https://image.slidesharecdn.com/cineticaquimica-140629102500-phpapp02/85/Cinetica-quimica-36-320.jpg)
![Reação genérica: 2A + 3B + C Produtos2A + 3B + C Produtos
Experimento [B]0(mol/L) Velocidade inicial da
reação (mol/L.min)
I 1 0,02
II 2 0,08
III 4 0,32](https://image.slidesharecdn.com/cineticaquimica-140629102500-phpapp02/85/Cinetica-quimica-37-320.jpg)
![Reação genérica:
2A + 3B + C Produtos2A + 3B + C Produtos
Experimento [C]0(mol/L) Velocidade inicial da
reação (mol/L.min)
I 1 0,02
II 2 0,02
III 4 0,02](https://image.slidesharecdn.com/cineticaquimica-140629102500-phpapp02/85/Cinetica-quimica-38-320.jpg)
![Reação genérica anterior
2A + 3B + C Produtos2A + 3B + C Produtos
QUAL A LEI DE VELOCIDADE QUE PODEMOS PROPOR?
V = K[A] [B] 2V = K[A] [B] 2
V = K[A] [B] 2V = K[A] [B] 2
V = K[A] [B] 2V = K[A] [B] 2
Concluindo...](https://image.slidesharecdn.com/cineticaquimica-140629102500-phpapp02/85/Cinetica-quimica-39-320.jpg)

![Ordem de reação (ordem global) é a soma dos valores das
potências a que as concentrações de reagentes se encontram
elevadas na equação cinética da reação (lei de velocidade).
Ordem de reação (ordem global) é a soma dos valores das
potências a que as concentrações de reagentes se encontram
elevadas na equação cinética da reação (lei de velocidade).
Consideremos a reação geral:
aA + bB → cC + dD
A equação da velocidade assume a forma:
Velocidade = k[A]α
[B]β
α, β,k – determinados experimentalmente
α e β– ordem de uma reação; α é a ordem de A e β é a ordem de B.
A reação tem ordem global α + β
Ordem de uma reação](https://image.slidesharecdn.com/cineticaquimica-140629102500-phpapp02/85/Cinetica-quimica-41-320.jpg)

![Reações de ordem zero são raras;
A equação cinética é:
velocidade = k[A]0
ou
v=k
A velocidade de uma reação de ordem zero é
constante e independente das concentrações de
reagentes.
(A)
= N2O
(B)
2 N2O(g) 2N2 (g) + O2(g) (em platina aquecida)
Obs.: A concentração molar é maior em B, mas isso não afeta
a velocidade da reação, pois a superfície da platina pode
adsorver um determinado número de moléculas.
2 N2O(g) 2N2 (g) + O2(g) (em platina aquecida)
Obs.: A concentração molar é maior em B, mas isso não afeta
a velocidade da reação, pois a superfície da platina pode
adsorver um determinado número de moléculas.
Reação de ordem zero](https://image.slidesharecdn.com/cineticaquimica-140629102500-phpapp02/85/Cinetica-quimica-43-320.jpg)
![A equação concentração x tempo
É obtida da integração (cálculo integral, que é visto no
ensino superior) da equação da lei de velocidade.
Matemáticamente temos:
[A] = [A]0 – k t
Graficamente:
k=declividade
da reta](https://image.slidesharecdn.com/cineticaquimica-140629102500-phpapp02/85/Cinetica-quimica-44-320.jpg)
![Numa reação de primeira ordem a velocidade depende da
concentração de reagente elevada à potência unitária.
45
A ProdutosA Produtos
a) Diminuição da concentração do reagente com o
tempo.
v=k[A]
Reação de ordem 1](https://image.slidesharecdn.com/cineticaquimica-140629102500-phpapp02/85/Cinetica-quimica-45-320.jpg)
![velocidade=−
Δ[A]
Δt
velocidade=k [A]
⇔ln[A]=ln[A]0−kt
46
A ProdutosA Produtos
(equação da reta)
b) Utilização da representação
gráfica da relação linear de ln[A] em
função do tempo para calcular a
constante de velocidade.](https://image.slidesharecdn.com/cineticaquimica-140629102500-phpapp02/85/Cinetica-quimica-46-320.jpg)
![Tempo de meia vida (T1/2): Reação
de primeira ordem
47
Variação da concentração
de um reagente com o número
de tempos de meia vida (t1/2)
para uma reação de primeira
ordem.
t=t1/2
[A] = [A]0/2
Tempo de de meia-vida (t1/2): é o tempo necessário para que a concentração
de uma reagente diminua para metade do seu valor inicial.
t1/2=
1
k
ln
[ A]0
[ A]0/ 2
⇔t1/2=
1
k
ln2⇔t1/ 2=
0,693
k](https://image.slidesharecdn.com/cineticaquimica-140629102500-phpapp02/85/Cinetica-quimica-47-320.jpg)
![É a reação cuja velocidade depende da concentração de
reagente elevada ao quadrado ou de concentrações de dois
reagentes diferentes, cada um deles elevada à unidade.
A → produto
48
velocidade=−
Δ[ A]
Δt
velocidade=k [ A]2
⇔
1
[ A]
=
1
[ A0 ]
+kt
Reação de ordem 2
(equação da reta)](https://image.slidesharecdn.com/cineticaquimica-140629102500-phpapp02/85/Cinetica-quimica-48-320.jpg)
![Podemos obter uma equação para
o tempo de meia-vida da reação
de 2ª ordem, se fizermos
[A] = [A]0/2 na equação:
1
[ A]
=
1
[ A]0
+kt
1
[A]0 /2
=
1
[A]0
+kt1/2 ⇔t1/2=
1
k [ A]0
Tempo de meia vida (T1/2): Reação
de segunda ordem](https://image.slidesharecdn.com/cineticaquimica-140629102500-phpapp02/85/Cinetica-quimica-49-320.jpg)
![Ordem Equação Cinética Equação
Concentração x
Tempo
Tempo de Meia
Vida
0 Velocidade =k [A] = [A]0 - kt
1 Velocidade = k [A] ln[A] = ln[A]0 - kt
2 Velocidade = k [A]2
1
[A]
=
1
[A]0
+ kt
t½
ln2
k
=
t½ =
[A]0
2k
t½ =
1
k[A]0
Resumindo...](https://image.slidesharecdn.com/cineticaquimica-140629102500-phpapp02/85/Cinetica-quimica-50-320.jpg)



![Vamos
exercitar!
A sacarose (C12H22O11) se decompõe em glicose e frutose em
solução ácida. A velocidade da reação é dada por:
V = k[sacarose].
Sabendo que K = 0,208 h-1
a 25ºC, qual o tempo necessário para
que 87,5% da concentração inicial de sacarose reaja nessa
temperatura?
Questão 2](https://image.slidesharecdn.com/cineticaquimica-140629102500-phpapp02/85/Cinetica-quimica-54-320.jpg)
