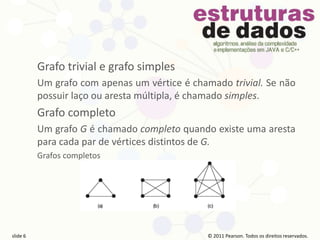
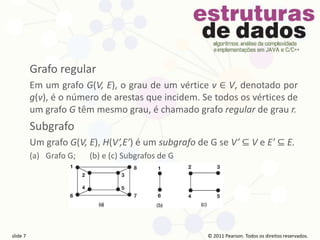
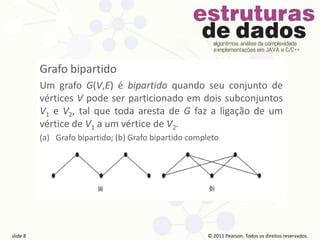
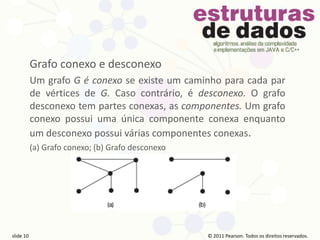
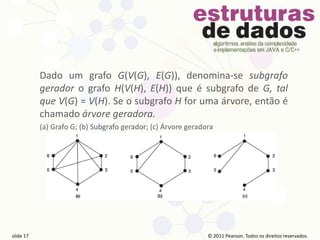
O documento apresenta conceitos básicos sobre teoria dos grafos, incluindo definições de vértices, arestas, caminhos, ciclos, grafos conexos e desconexos, árvores e outros. As informações são apresentadas em 16 slides com direitos autorais da Pearson Prentice Hall para uso educacional.














![© 2011 Pearson Prentice Hall. Todos os direitos reservados.
slide 21 © 2011 Pearson Prentice Hall. Todos os direitos reservados.
slide 21 © 2011 Pearson Prentice Hall. Todos os direitos reservados.
slide 21 © 2011 Pearson Prentice Hall. Todos os direitos reservados.
slide 21
© 2011 Pearson. Todos os direitos reservados.
slide 21
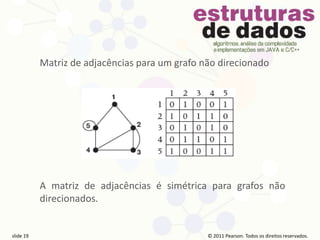
Lista de adjacências
Consiste em um vetor Adj com n =|V| entradas, uma
para cada vértice do grafo. Cada entrada Adj[v] possui
uma lista encadeada de vértices adjacentes a v em G.
Não existe uma ordem dos vértices nessa lista.
Compõe-se de n listas de 2m elementos, onde m é o
número de arestas. O espaço utilizado é O(n + m).](https://image.slidesharecdn.com/captulo8-algoritmosemgrafos-240404235109-3002bf01/85/Capitulo-8-Algoritmos-em-grafos-com-Pseudocodigos-e-em-Java-21-320.jpg)





