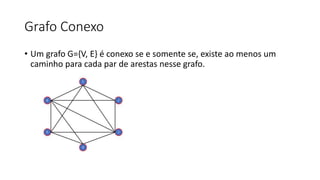
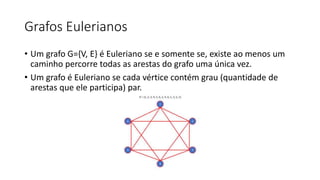
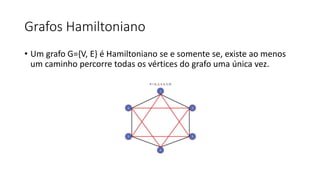
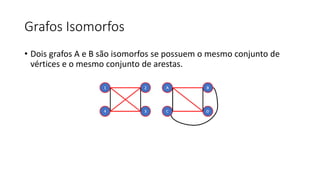
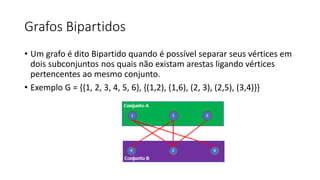
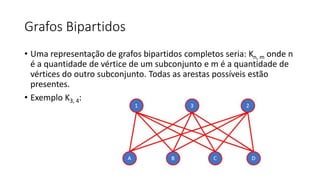
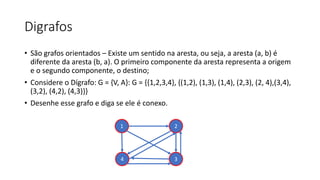
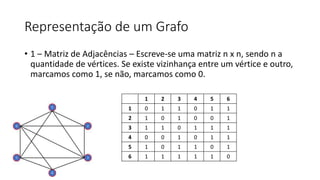
1. O documento define e descreve vários tipos de grafos e suas propriedades, incluindo caminhos, grafos conexos, grafos eulerianos e hamiltonianos. 2. Também apresenta grafos completos, isomorfos, bipartidos e digrafos, além de métodos de representação de grafos como matriz de adjacências. 3. Discutem propriedades e exemplos de cada um desses tipos e conceitos de grafos.

1. Tipos de Grafos e Definições
Matemática Discreta – Marcelo Arantes

2. Caminho
• Caminho é uma sequencia de arestas que ligam um vértice origem a um
vértice destino. Exemplo: apresente 3 caminhos de 1 para 4 no grafo
abaixo: C1 = {1,2,3,4}, C2 = {1, 5, 4}, C3 = {1, 5, 3, 4}, C4 = {1,6,1,6,4}.
• Existem quantos caminhos para ligar 1 a 4 no grafo abaixo?
• Ciclo – Um ciclo é um caminho que leva um vértice até ele mesmo ...
• Tamanho do caminho é dado pela quantidade de arestas presentes no
caminho.

3. Grafo Conexo
• Um grafo G={V, E} é conexo se e somente se, existe ao menos um
caminho para cada par de arestas nesse grafo.

4. Grafos Eulerianos
• Um grafo G={V, E} é Euleriano se e somente se, existe ao menos um
caminho percorre todas as arestas do grafo uma única vez.
• Um grafo é Euleriano se cada vértice contém grau (quantidade de
arestas que ele participa) par.

5. Grafos Hamiltoniano
• Um grafo G={V, E} é Hamiltoniano se e somente se, existe ao menos
um caminho percorre todas os vértices do grafo uma única vez.

6. Grafos Completos - Kruskal
• Um grafo G={V, E} é dito completo quando cada vértice possui uma
aresta que conecta diretamente esse cada um dos outros vértices.
Chamamos esses grafos de grafos K.
• K2 = {{1, 2}, {(1, 2)}}
• K3 = {{1, 2, 3}, {(1, 2), (1, 3), (2, 3)}
• K4 = {{1, 2, 3, 4}, {(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)}
• Desenhe o K5 e o K6

7. Grafos Isomorfos
• Dois grafos A e B são isomorfos se possuem o mesmo conjunto de
vértices e o mesmo conjunto de arestas.

8. Grafos Bipartidos
• Um grafo é dito Bipartido quando é possível separar seus vértices em
dois subconjuntos nos quais não existam arestas ligando vértices
pertencentes ao mesmo conjunto.
• Exemplo G = {{1, 2, 3, 4, 5, 6}, {(1,2), (1,6), (2, 3), (2,5), (3,4)}}

9. Grafos Bipartidos
• Uma representação de grafos bipartidos completos seria: Kn, m onde n
é a quantidade de vértice de um subconjunto e m é a quantidade de
vértices do outro subconjunto. Todas as arestas possíveis estão
presentes.
• Exemplo K3, 4:

10. Digrafos
• São grafos orientados – Existe um sentido na aresta, ou seja, a aresta (a, b) é
diferente da aresta (b, a). O primeiro componente da aresta representa a origem
e o segundo componente, o destino;
• Considere o Dígrafo: G = {V, A}: G = {{1,2,3,4}, {(1,2), (1,3), (1,4), (2,3), (2, 4),(3,4),
(3,2), (4,2), (4,3)}}
• Desenhe esse grafo e diga se ele é conexo.
1
3
2
4

11. Representação de um Grafo
• 1 – Matriz de Adjacências – Escreve-se uma matriz n x n, sendo n a
quantidade de vértices. Se existe vizinhança entre um vértice e outro,
marcamos como 1, se não, marcamos como 0.
1 2 3 4 5 6
1 0 1 1 0 1 1
2 1 0 1 0 0 1
3 1 1 0 1 1 1
4 0 0 1 0 1 1
5 1 0 1 1 0 1
6 1 1 1 1 1 0

12. • São grafos orientados. Existe um sentido na aresta, ou seja, a aresta
(a, b) é diferente da aresta (b, a). O primeiro componente da aresta
representa a origem e o segundo componente. O destino.
• 1 - São grafos orientados.
• 2 - Existe um sentido na aresta, ou seja, a aresta (a, b) é diferente da
aresta (b, a).
• 3 - O primeiro componente da aresta representa a origem e o
segundo componente.
• 4 - O destino.

13. • 1 - São grafos orientados.
• 2 - Existe sentido aresta, seja, aresta diferente aresta.
• 3 - primeiro componente aresta representa origem segundo
componente.
• 4 - destino.
São, grafos, orientados, existe, sentido, aresta, seja, diferente, primeiro,
componente, representa, origem, segundo, destino.

14. 1
2
3
4
São
grafos
orientados
existe
sentido
aresta
seja
diferente
segundo
primeiro
componente
representa
origem
destino
1- São grafos
orientados.
2- Existe um sentido
na aresta, ou seja, a
aresta (a, b) é
diferente da aresta
(b, a).
3- O primeiro
componente da
aresta representa a
origem e o segundo
componente.
4- O destino.
3
2

15. 1
2
3
4
São
grafos
orientados
existe
sentido
aresta
seja
diferente
segundo
primeiro
componente
representa
origem
destino
3
2
1 2 3 4
São 1 0 0 0
Grafos 1 0 0 0
orientados 1 0 0 0
Existe 0 1 0 0
Sentido 0 1 0 0
Aresta 0 3 1 0
Seja 0 1 0 0
Diferente 0 1 0 0
Primeiro 0 0 1 0
Componente 0 0 2 0
Representa 0 0 1 0
Origem 0 0 1 0
Segundo 0 0 1 0
destino 0 0 0 1