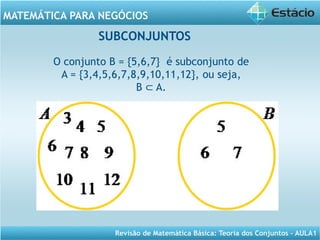
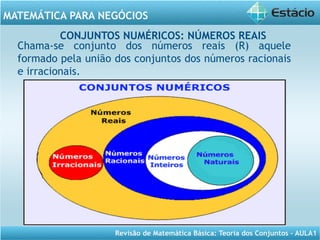
Este documento apresenta a primeira aula de uma disciplina de Matemática para Negócios. A aula aborda a Teoria dos Conjuntos, definindo conceitos básicos como união, interseção e diagramas de Venn, e exemplificando com conjuntos numéricos. O documento também traz exercícios sobre aplicação desses conceitos.