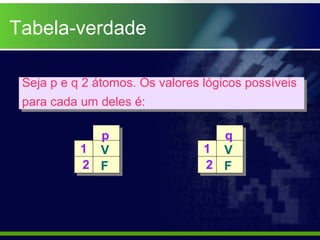
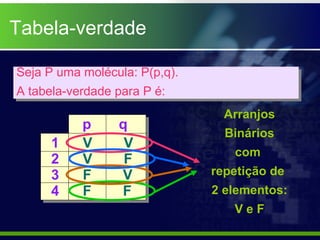
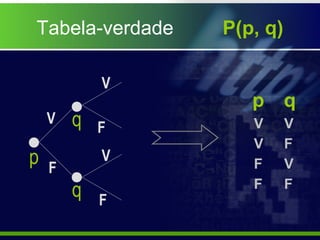
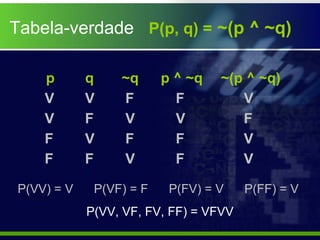
O documento explica o que é uma tabela-verdade e como ela é usada para determinar os valores lógicos possíveis de proposições compostas com base nos valores das proposições simples que as compõem. É mostrado como tabelas-verdade para diferentes conectivos lógicos como conjunção, disjunção, condicional e bicondicional produzem resultados distintos.

1. Ensino Superior
2 – Tabela-Verdade
Amintas Paiva Afonso
Lógica Matemática e Computacional

2. Tabela-verdade
A TABELA-VERDADE é um recurso utilizado
para determinar todos os possíveis valores
lógicos de uma proposição composta, a partir
de todas as possíveis atribuições de valores
lógicos dados às proposições simples que a
compõem.
O resultado depende do conectivo que gera a
proposição composta. Conectivos diferentes
geram tabelas-verdade diferentes.

3. Seja p e q 2 átomos. Os valores lógicos possíveis
para cada um deles é:
Seja p e q 2 átomos. Os valores lógicos possíveis
para cada um deles é:
p
1
2
V
F
q
1
2
V
F
Tabela-verdade

4. Seja P uma molécula: P(p,q).
A tabela-verdade para P é:
Seja P uma molécula: P(p,q).
A tabela-verdade para P é:
p q
1 V V
2 V F
3 F V
4 F F
Arranjos
Binários
com
repetição de
2 elementos:
V e F
Tabela-verdade

5. Tabela-verdade P(p, q)
p q
p
V
F
q
q
V
F
V
F
V
V
V
V
F
F
F
F

6. Seja Q uma molécula: Q(p,q,r).Seja Q uma molécula: Q(p,q,r).
Arranjos
Ternários
com
repetição de
2 elementos:
V e F
p q r
1 V V V
2 V V F
3 V F V
4 V F F
5 F V V
6 F V F
7 F F V
8 F F F
Tabela-verdade

7. NOTAÇÃO
V(p): Valor lógico da proposição atômica p.
V(p) = V ou V(p) =F
V(P): Valor lógico da proposição molecular P.
V(P) = V ou V(P) = F
Tabela-verdade

8. Tabela-verdade da CONJUNÇÃO (E)
p q p ^ q
EXEMPLOS:
“Elefantes são grandes e bolas são redondas.”
“A lua é quadrada e a neve é branca .”
V
V
V
V
F
F
F
F
F
V
F
F

9. Tabela-verdade da Disjunção: (OU)
p q p v q
EXEMPLOS:
“A lua é redonda ou a neve é branca.”
“Hoje é terça ou quarta.”
V
V
V
V
V
F
F
F
V
V
F
F

10. Tabela-Verdade CONDICIONAL: (Se então)
p q p → q
EXEMPLOS:
“Se tem fumaça então tem fogo.”
“Se hoje é domingo então tem jogo na televisão.”
V
V
V
V
F
F
F
F
V
V
V
F

11. Tabela-Verdade BI-CONDICIONAL
(Se e somente se)
p q p ↔ q
EXEMPLOS:
“José faz aniversário se e somente se estamos no mês de abril.”
“Hoje é domingo se e somente se tem jogo na televisão.”
V
V
V
V
F
F
F
F
F
V
V
F

12. Tabela-verdade P(p, q) = ~(p ^ ~q)
p q ~q p ^ ~q ~(p ^ ~q)
V
V
V
V
V V
V
V
V
F
F
F
F
V
F
F
F
F
F
F
P(VV) = V P(VF) = F P(FV) = V P(FF) = V
P(VV, VF, FV, FF) = VFVV

13. P(p, q) = ~(p ^ q) v ~(q↔p)
p q p ^ q
q ↔
p
~(p ^
q)
~(q↔p
)
~(p ^ q) v
~(q↔p)
V
V
V
V
F F
F
P(VV) = F P(VF) = V P(FV) = V P(FF) = V
P(VV, VF, FV, FF) = FVVV
F
V
V
V
F
V
FF
F
F
F
FV V
V
V
V
V
V
F F

14. Tabela-verdade P(p, q, r)
p q r
V
V
V
V
F
F
F
F
V
V
F
V
F
F F
F
F
V
V
V
V
V
FF

15. p q r ~q v r
Tabela-verdade P(p, q, r) = ~q v r
V
V
V
V
F
F
F
F
V
V
F
V
F
F F
F
F
V
V
V
V
V
FF
F
V
V
V
F
V
V
V

16. p q r ~q v r p ^ (~q v r)
Tabela-verdade P(p, q, r) = p ^ (~q v r)
V
V
V
V
F
F
F
F
V
V
F
V
F
F F
F
F
V
V
V
V
V
FF
F
V
V
V
F
F
F
F
F
V
V
V
F
V
V
V

17. p q r ~r p v ~r q ^ ~r p v ~r → q ^ ~r
P(p, q, r) = p v ~r → q ^ ~r
V
V
V
V
F
F
F
F
V
V
V
F
V
F
F F
F
F
F
V
V
V
V
V
V
FF
F
F
F
F
F
F
F
F
F
F
F
F
V
V
V
V
V
V
V
V
V V
V
V
V
V
F
F
F
P(VVV, VVF, VFV, VFF, FVV, FVF, FFV, FFF) = FVVFVVVF

18. p q r p → q q → r p → r (p → q) ^ (q → r) → (p → r)
P(p, q, r) = (p → q) ^ (q → r) → (p →
r)
V
V
V
V
F
F
F
F
V
V
F
F
V
F
F F
F
F
F
V
V
V
V
V
V
FF
V
V
V
V
V
V
V
F
V
V
V
V
V
V
V
F
V
V
V
V
F V
F
V
V
V
V
V
V
P(VVV, VVF, VFV, VFF, FVV, FVF, FFV, FFF) = VVVVVVVV

19. p q r ~q ~qvr p↔~r p→(~qvr) qv(p↔~r) ~(qv(p↔~r)) P
P(p, q, r) = (p → (~q v r)) ^ ~(q v (p ↔ ~r))
V
V
V
V
F
F
F
F
V
V
V
F
V
F
F F
F
V
F
V
F
V
V
V
V
FF
F
V
F
F
V
V
V
V
F
V
V
F
F
V
F
F
V
V
V
V
F F
V
V
V
V
V
V
V
P(VVV, VVF, VFV, VFF, FVV, FVF, FFV, FFF) = FFVFFFFV
V
F
V
V
V
V
F
V
F
V
F
F
F
F
V
F
F
V
F
F
F
F
V
F

20. Tabela-verdade
p q r ~q v r p ^ (~q v r) ~r ↔ q
V V V V V F
V V F F F V
V F V V V V
V F F V V F
F V V V F F
F V F F F V
F F V V F V
F F F V F F

21. Tabela-verdade
p q r ~q v r p ^ (~q v r) ~r ↔ q prop
V V V V V F
V V F F F V
V F V V V V
V F F V V F
F V V V F F
F V F F F V
F F V V F V
F F F V F F