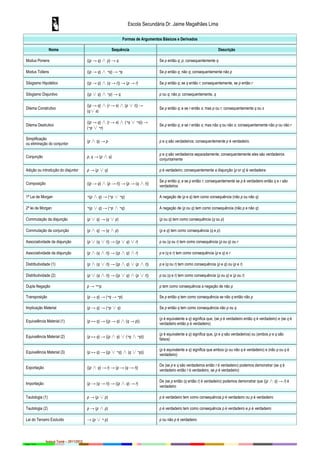
O documento lista vários argumentos lógicos básicos e derivados, incluindo modus ponens, modus tollens, silogismos hipotéticos e disjuntivos, dilemas construtivos e destrutivos, e as leis de Morgan, entre outros. Ele fornece os nomes latinos dos argumentos, suas fórmulas lógicas e breves descrições.

1. Escola Secundária Dr. Jaime Magalhães Lima
Formas de Argumentos Básicos e Derivados
Nome Sequência Descrição
Modus Ponens ((p → q) ∧ p) → q Se p então q; p; consequentemente q
Modus Tollens ((p → q) ∧ ¬q) → ¬p Se p então q; não q; consequentemente não p
Silogismo Hipotético ((p → q) ∧ (q → r)) → (p → r) Se p então q; se q então r; consequentemente, se p então r
Silogismo Disjuntivo ((p ∨ q) ∧ ¬p) → q p ou q; não p; consequentemente, q
((p → q) ∧ (r → s) ∧ (p ∨ r)) →
Dilema Construtivo Se p então q; e se r então s; mas p ou r; consequentemente q ou s
(q∨ s)
((p → q) ∧ (r → s) ∧ (¬q ∨ ¬s)) →
Dilema Destrutivo Se p então q; e se r então s; mas não q ou não s; consequentemente não p ou não r
(¬p ∨ ¬r)
Simplificação
(p ∧ q) → p p e q são verdadeiros; consequentemente p é verdadeiro.
ou eliminação do conjuntor
p e q são verdadeiros separadamente; consequentemente eles são verdadeiros
Conjunção p, q → (p ∧ q)
conjuntamente
Adição ou introdução do disjuntor p → (p ∨ q) p é verdadeiro; consequentemente a disjunção (p or q) é verdadeira
Se p então q; e se p então r; consequentemente se p é verdadeiro então q e r são
Composição ((p → q) ∧ (p → r)) → (p → (q ∧ r))
verdadeiros
1ª Lei de Morgan ¬(p ∧ q) → (¬p ∨ ¬q) A negação de (p e q) tem como consequência (não p ou não q)
2ª lei de Morgan ¬(p ∨ q) → (¬p ∧ ¬q) A negação de (p ou q) tem como consequência (não p e não q)
Commutação da disjunção (p ∨ q) → (q ∨ p) (p ou q) tem como consequência (q ou p)
Commutação da conjunção (p ∧ q) → (q ∧ p) (p e q) tem como consequência (q e p)
Associatividade da disjunção (p ∨ (q ∨ r)) → ((p ∨ q) ∨ r) p ou (q ou r) tem como consequência (p ou q) ou r
Associatividade da disjunção (p ∧ (q ∧ r)) → ((p ∧ q) ∧ r) p e (q e r) tem como consequência (p e q) e r
Distributividade (1) (p ∧ (q ∨ r)) → ((p ∧ q) ∨ (p ∧ r)) p e (q ou r) tem como consequência (p e q) ou (p e r)
Distributividade (2) (p ∨ (q ∧ r)) → ((p ∨ q) ∧ (p ∨ r)) p ou (q e r) tem como consequência (p ou q) e (p ou r)
Dupla Negação p → ¬¬p p tem como consequência a negação de não p
Transposição (p → q) → (¬q → ¬p) Se p então q tem como consequência se não q então não p
Implicação Material (p → q) → (¬p ∨ q) Se p então q tem como consequência não p ou q
(p é equivalente a q) significa que, (se p é verdadeiro então q é verdadeiro) e (se q é
Equivalência Material (1) (p ↔ q) → ((p → q) ∧ (q → p))
verdadeiro então p é verdadeiro)
(p é equivalente a q) significa que, (p e q são verdadeiros) ou (ambos p e q são
Equivalência Material (2) (p ↔ q) → ((p ∧ q) ∨ (¬q ∧ ¬p))
falsos)
(p é equivalente a q) significa que ambos (p ou não q é verdadeiro) e (não p ou q é
Equivalência Material (3) (p ↔ q) → ((p ∨ ¬q) ∧ (q ∨ ¬p))
verdadeiro)
De (se p e q são verdadeiros então r é verdadeiro) podemos demonstrar (se q é
Exportação ((p ∧ q) → r) → (p → (q → r))
verdadeiro então r é verdadeiro, se p é verdadeiro)
De (se p então (q então r) é verdadeiro) podemos demonstrar que ((p ∧ q) → r) é
Importação (p → (q → r)) → ((p ∧ q) → r)
verdadeiro
Tautologia (1) p → (p ∨ p) p é verdadeiro tem como consequência p é verdadeiro ou p é verdadeiro
Tautologia (2) p → (p ∧ p) p é verdadeiro tem como consequência p é verdadeiro e p é verdadeiro
Lei do Terceiro Excluído → (p ∨ ¬ p) p ou não p é verdadeiro
Isaque Tomé – 2011/2012
Isaque Tomé