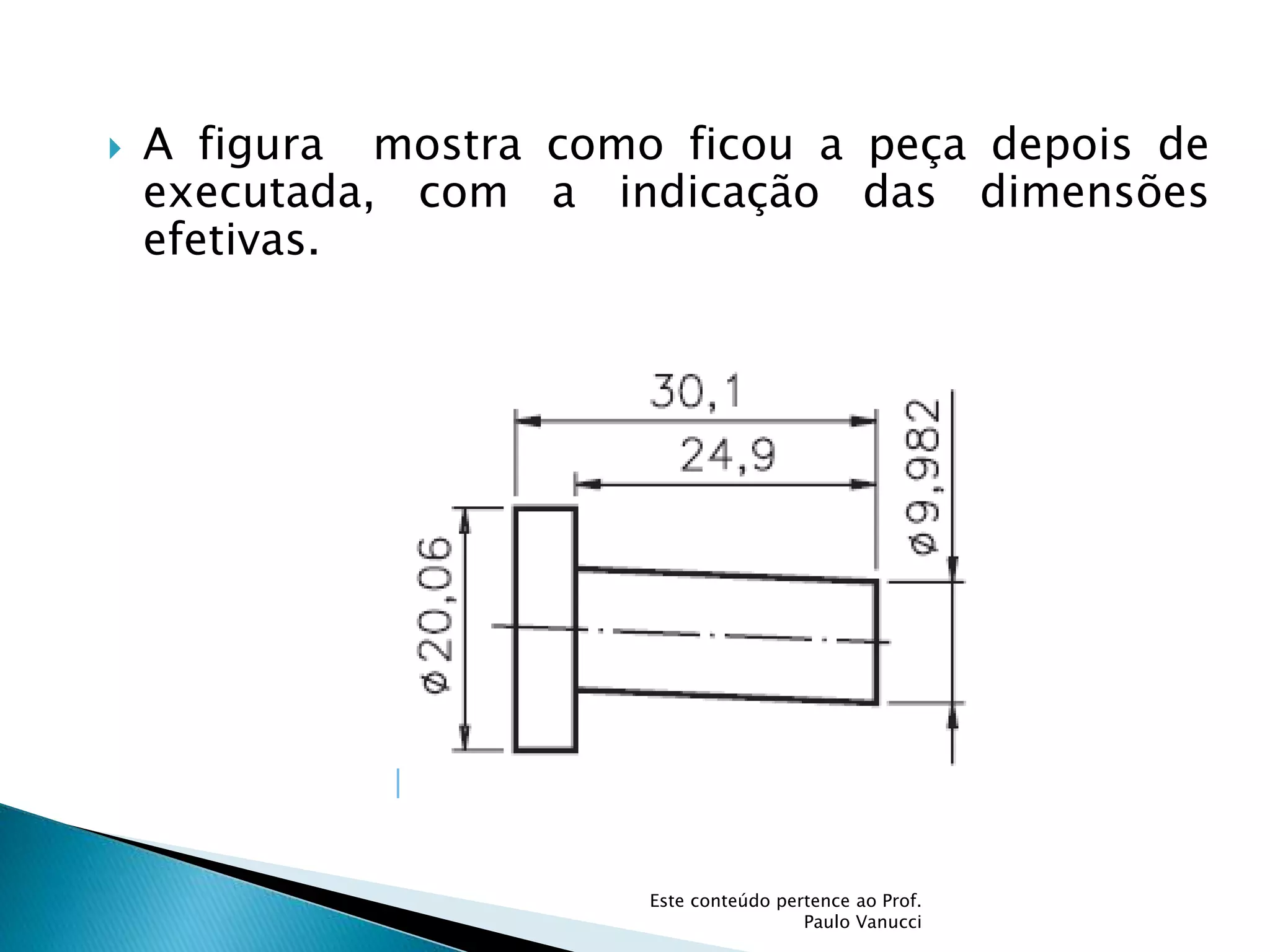
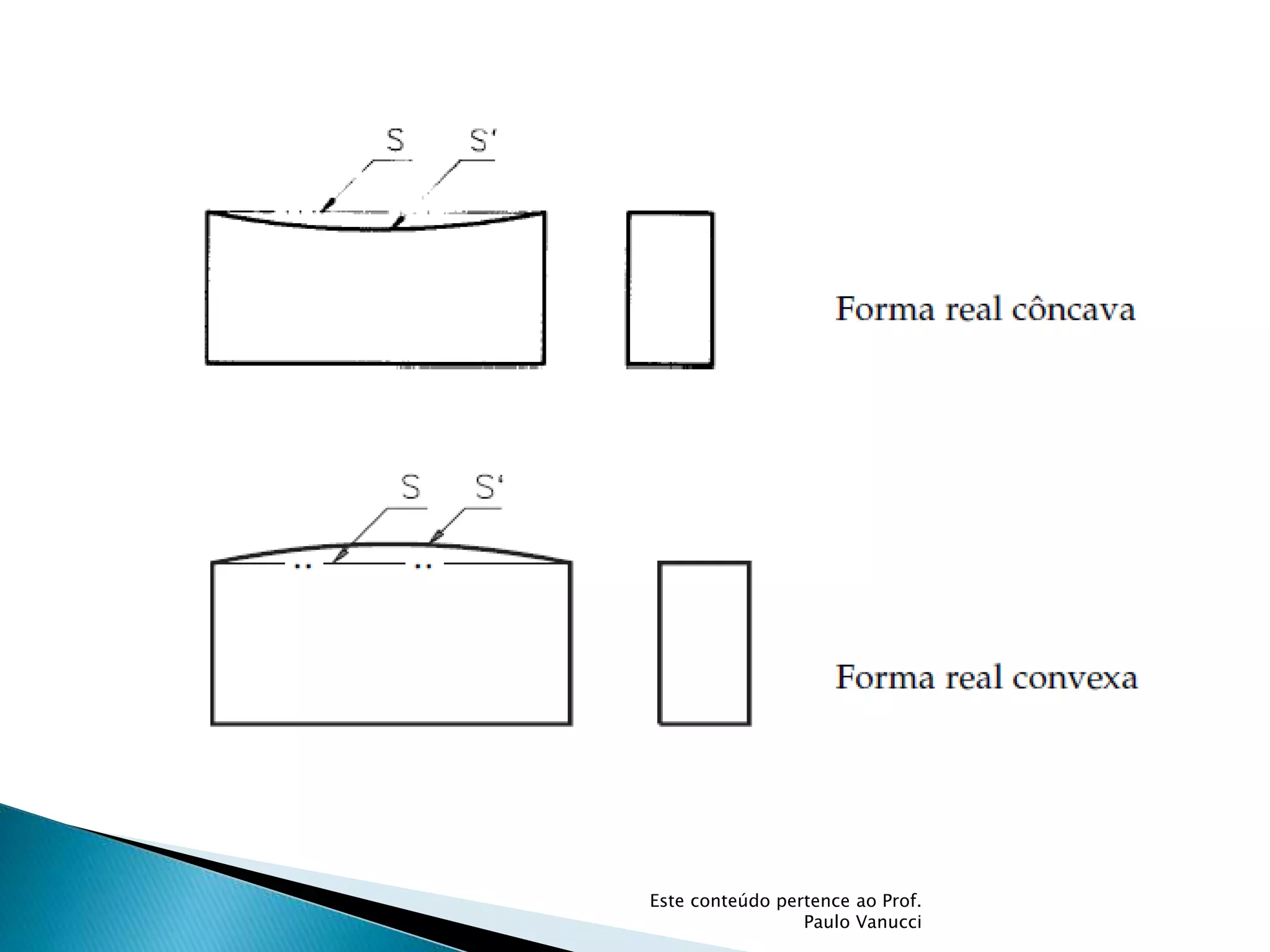
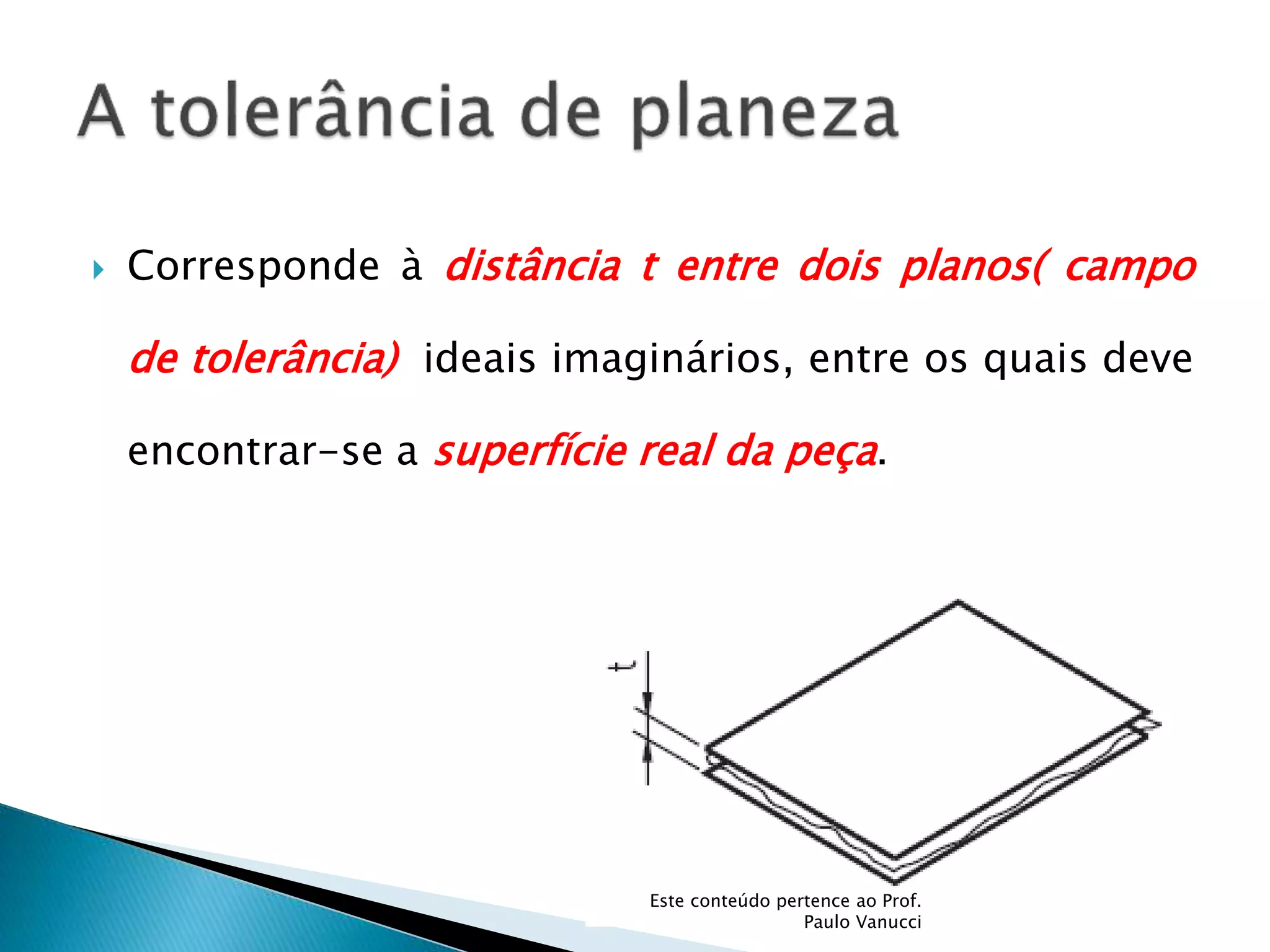
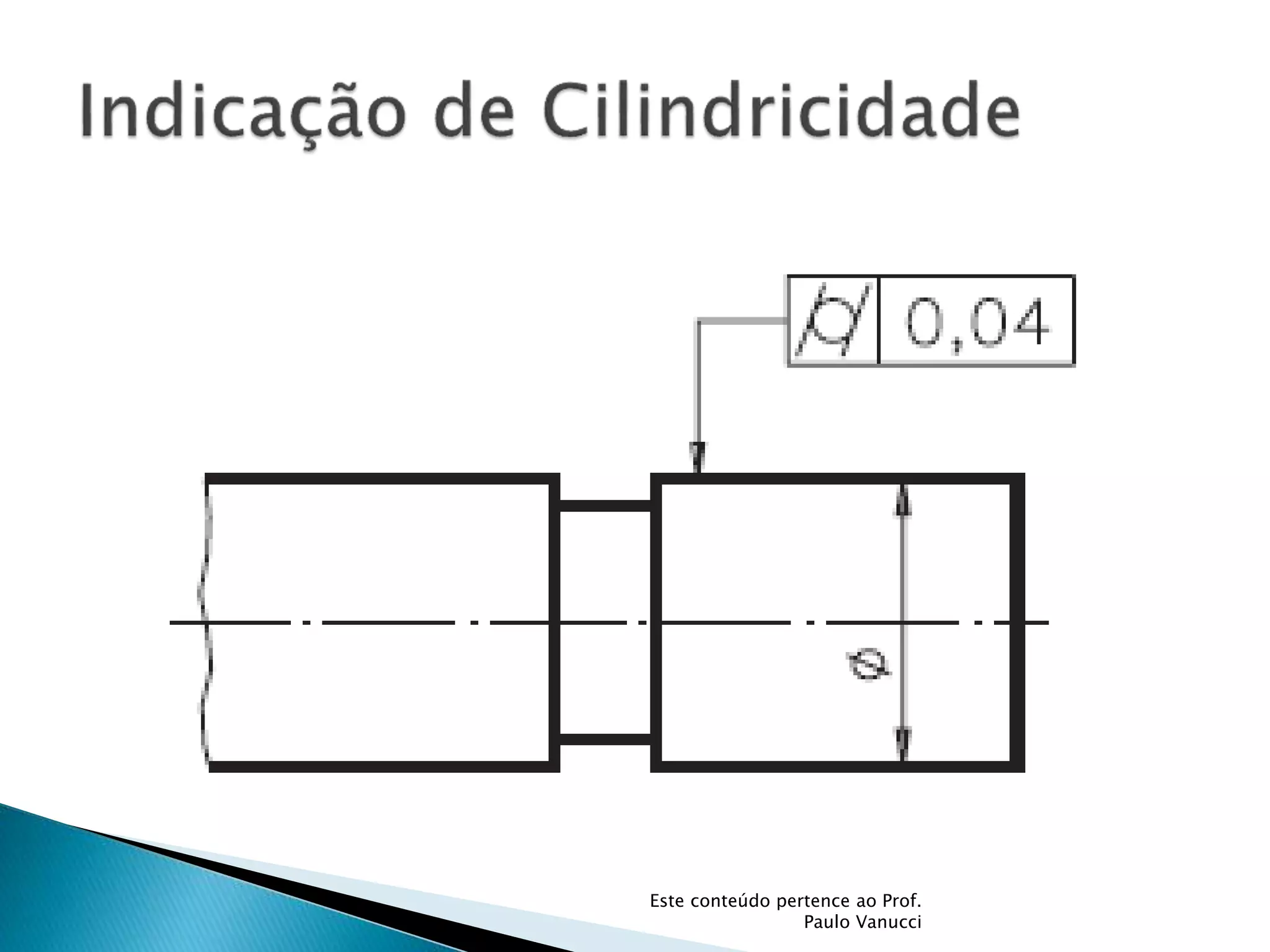
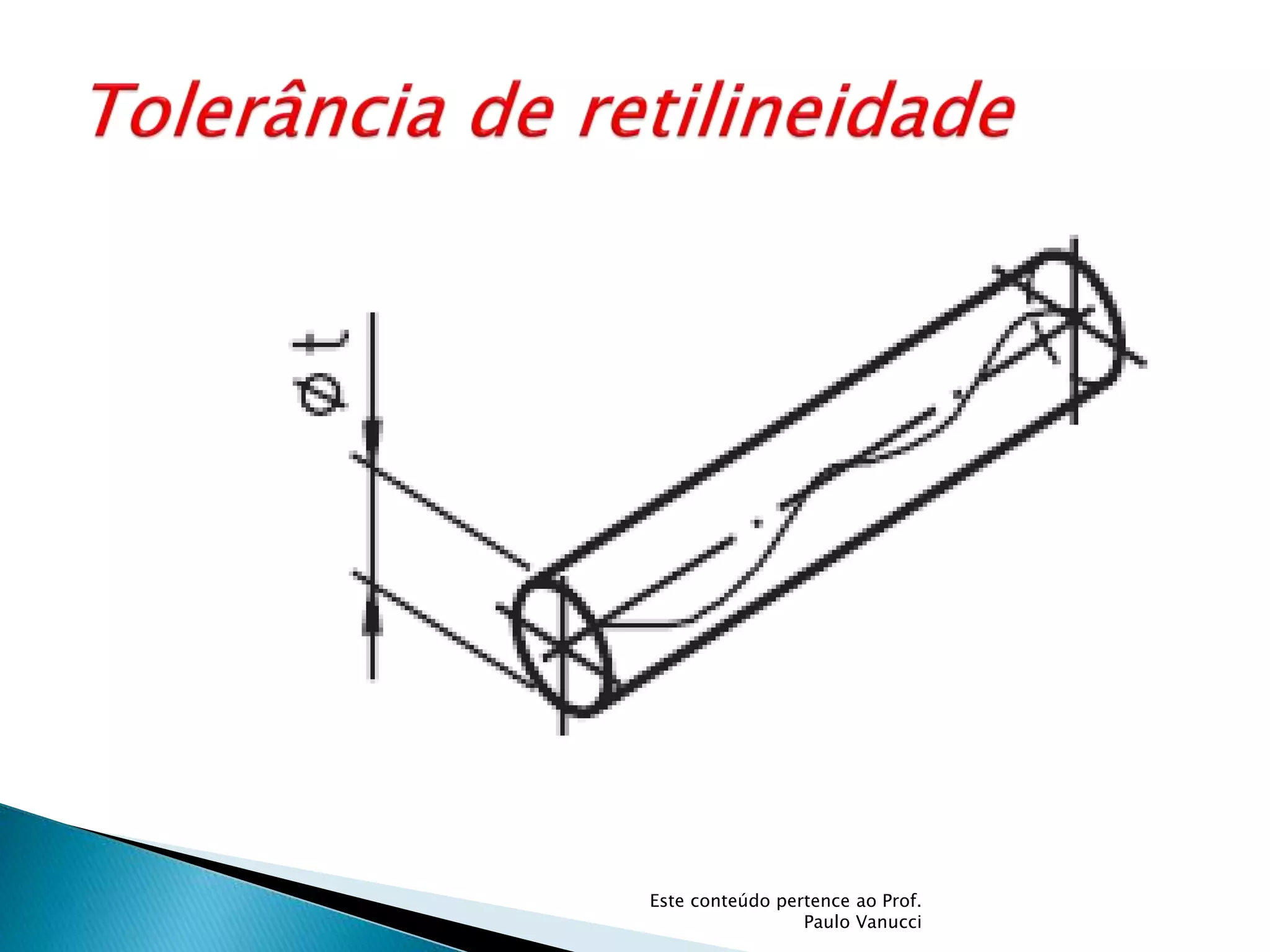
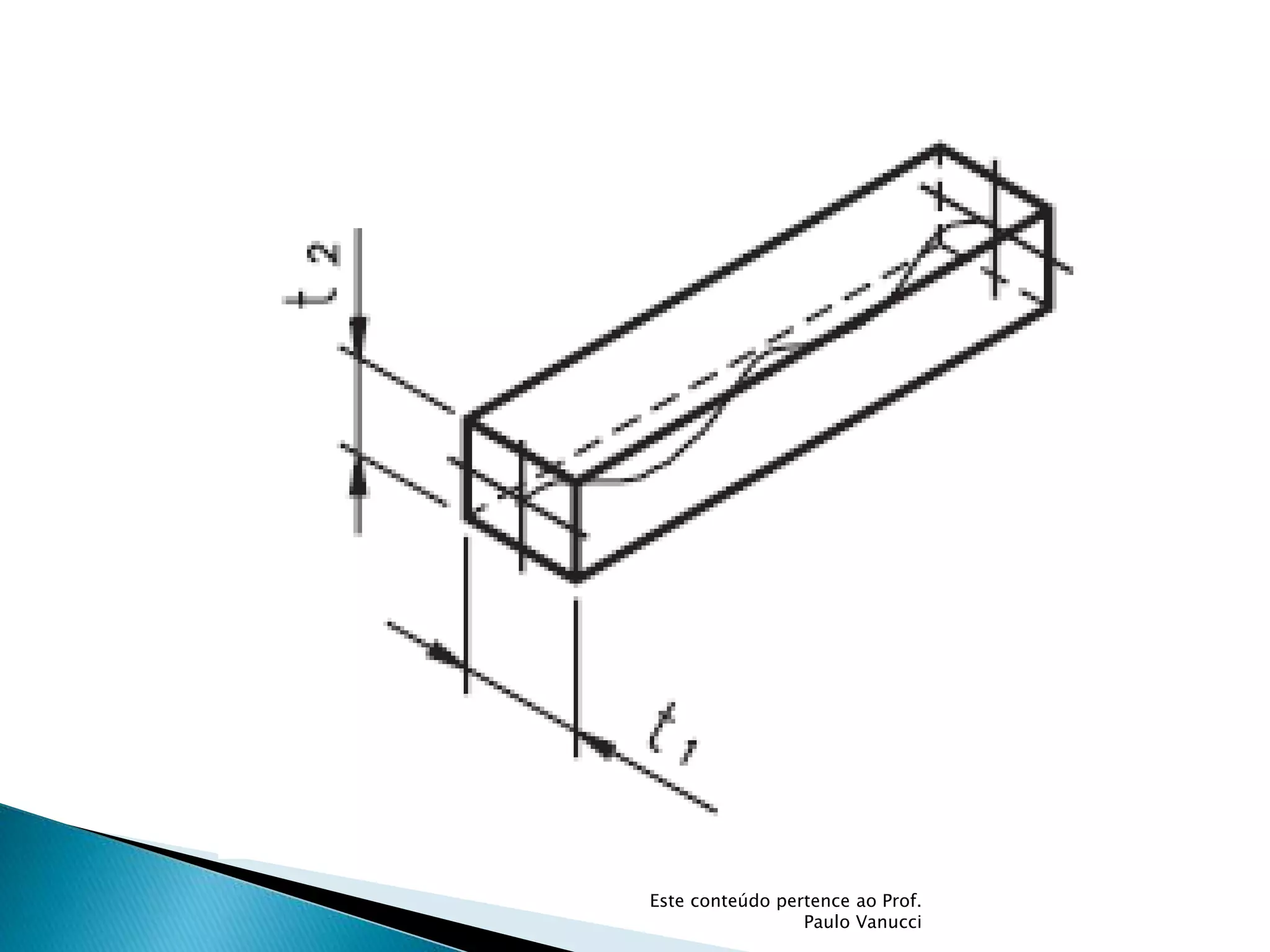
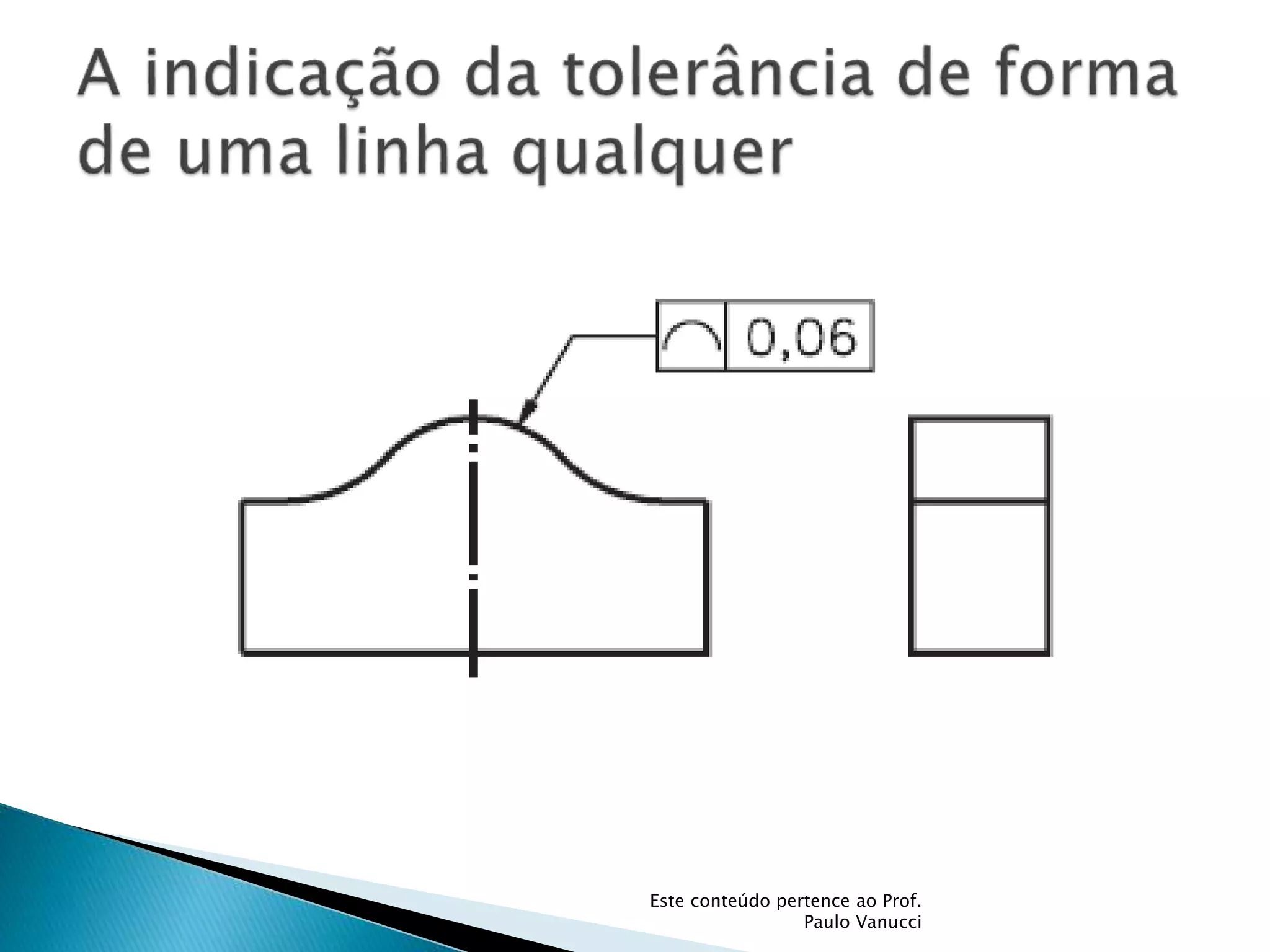
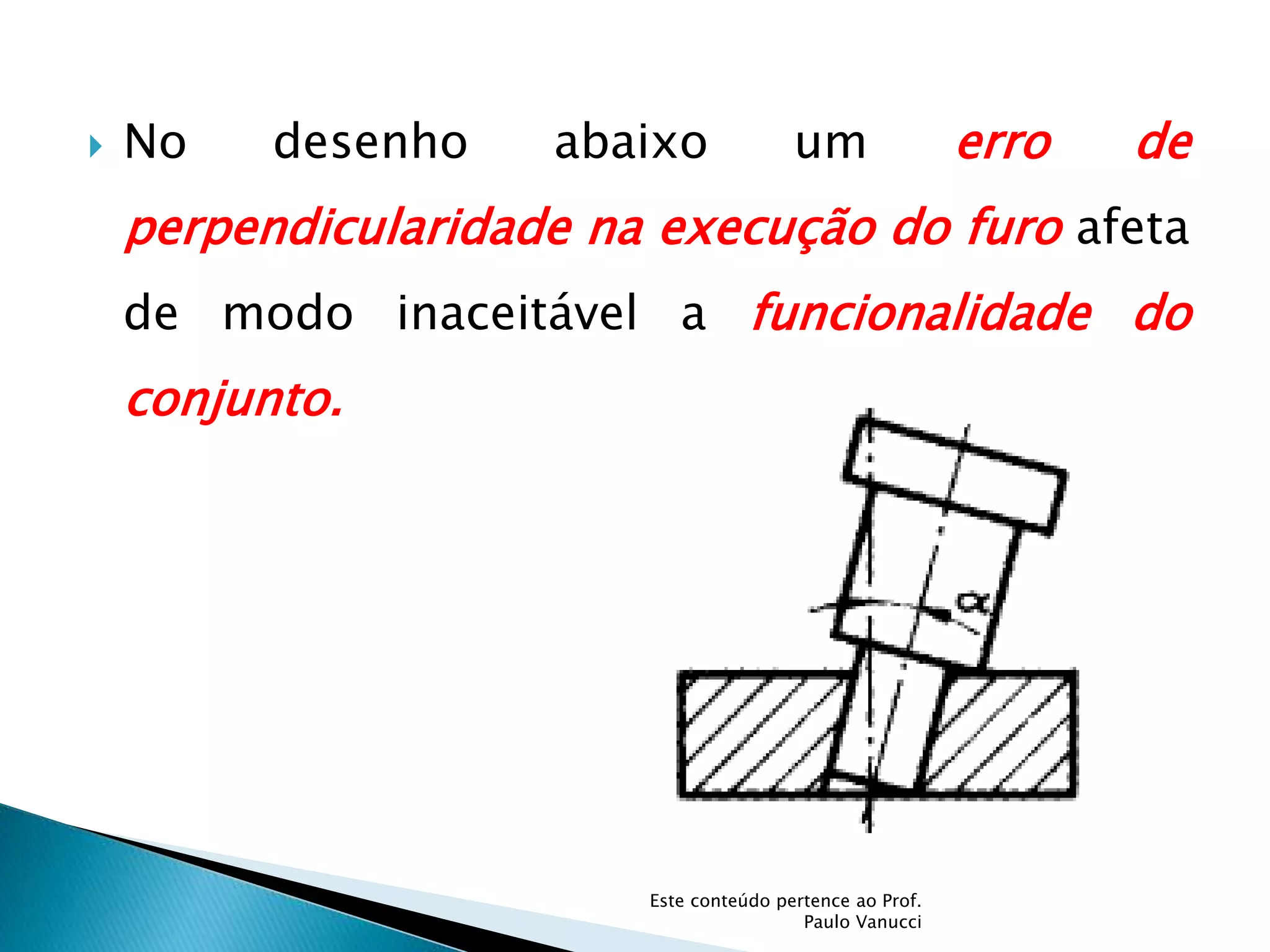
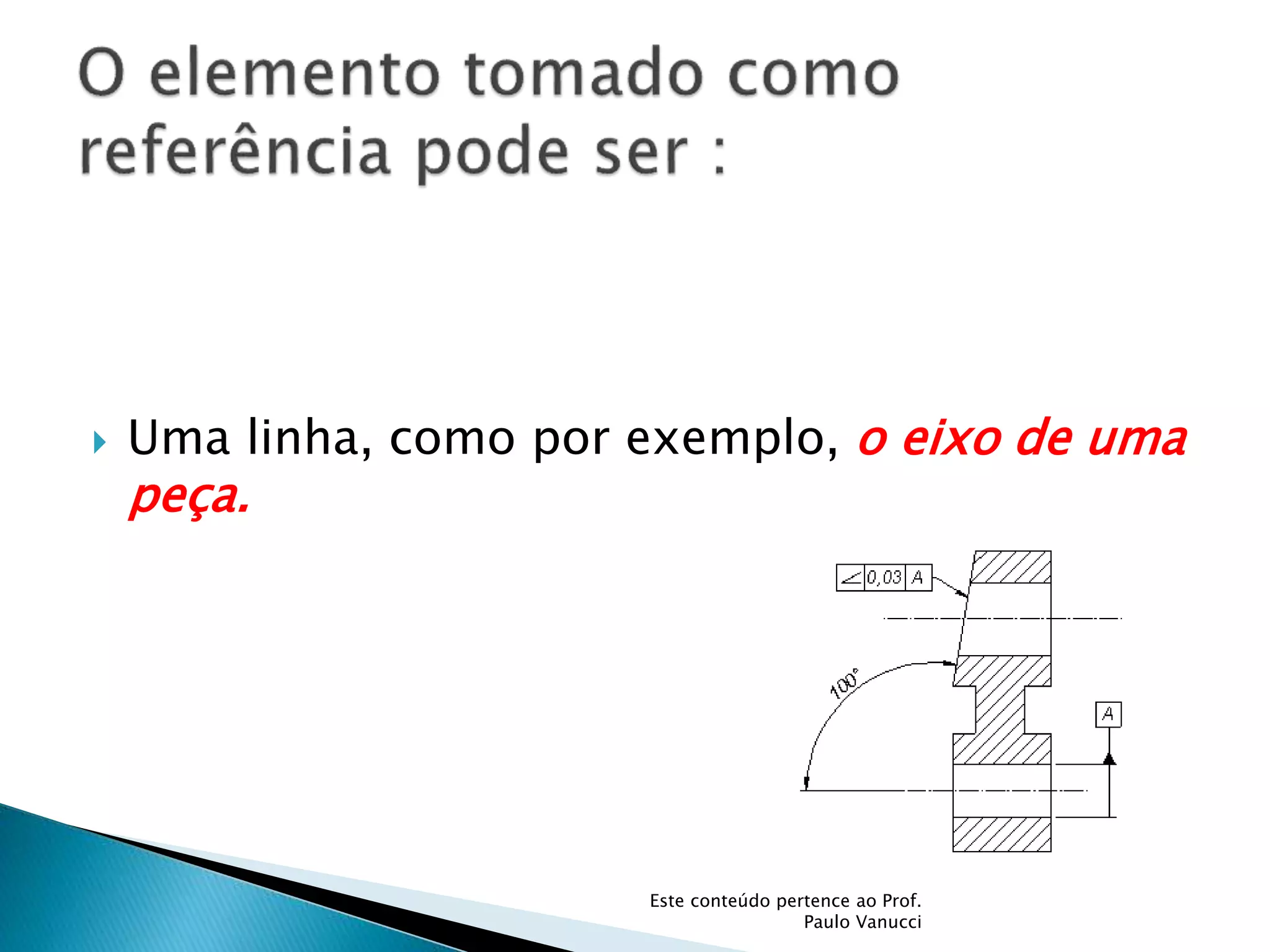
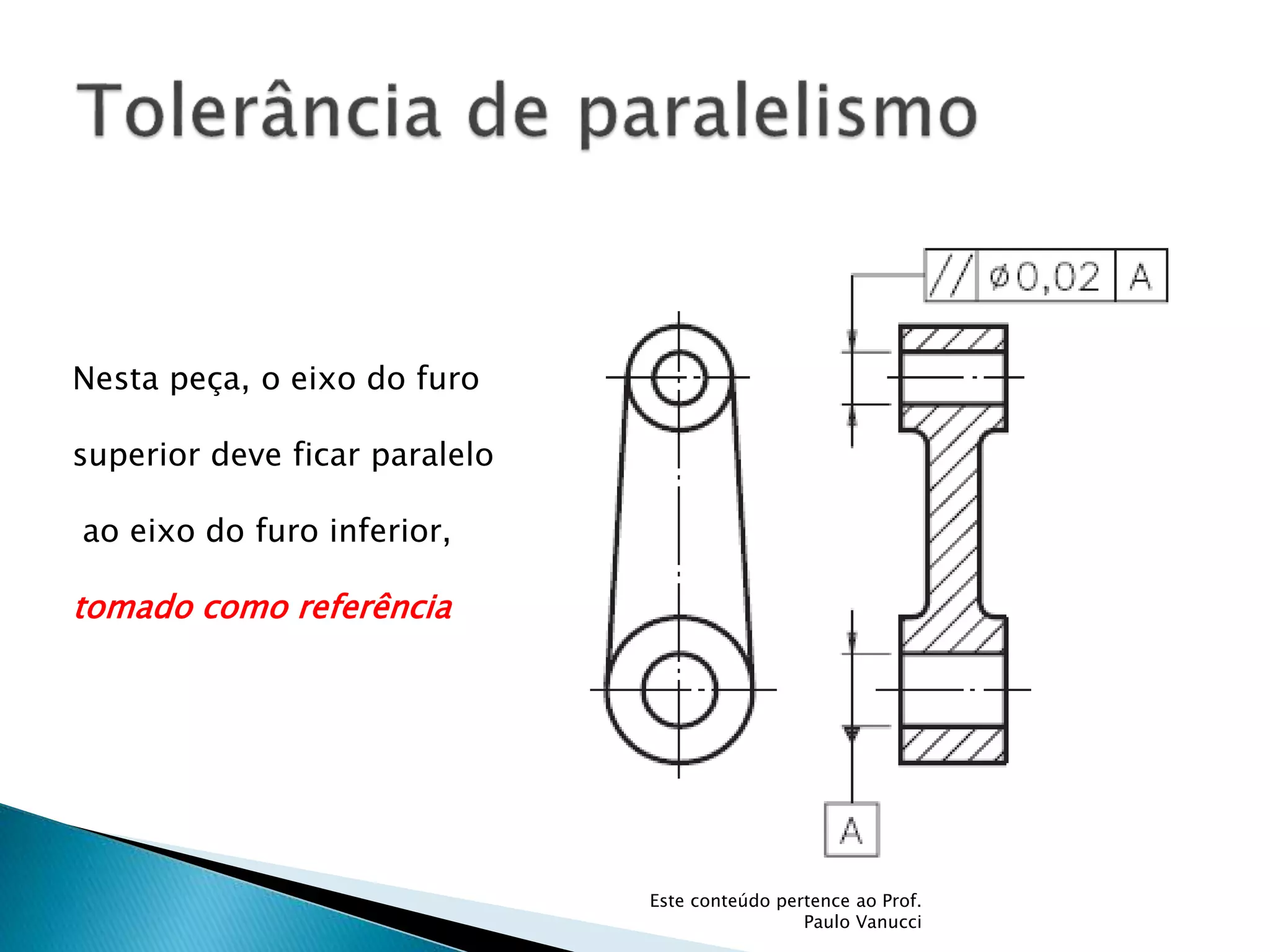
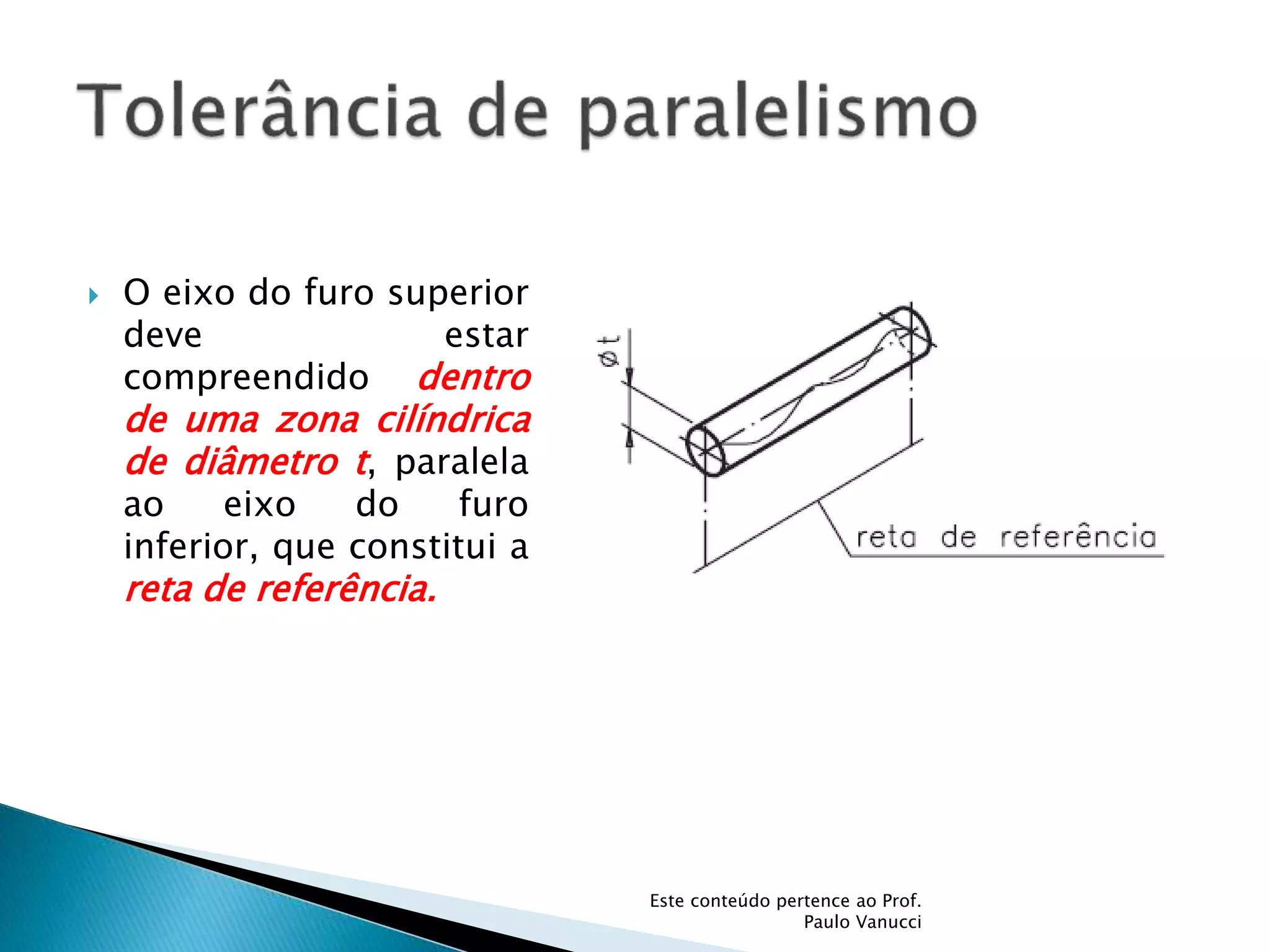
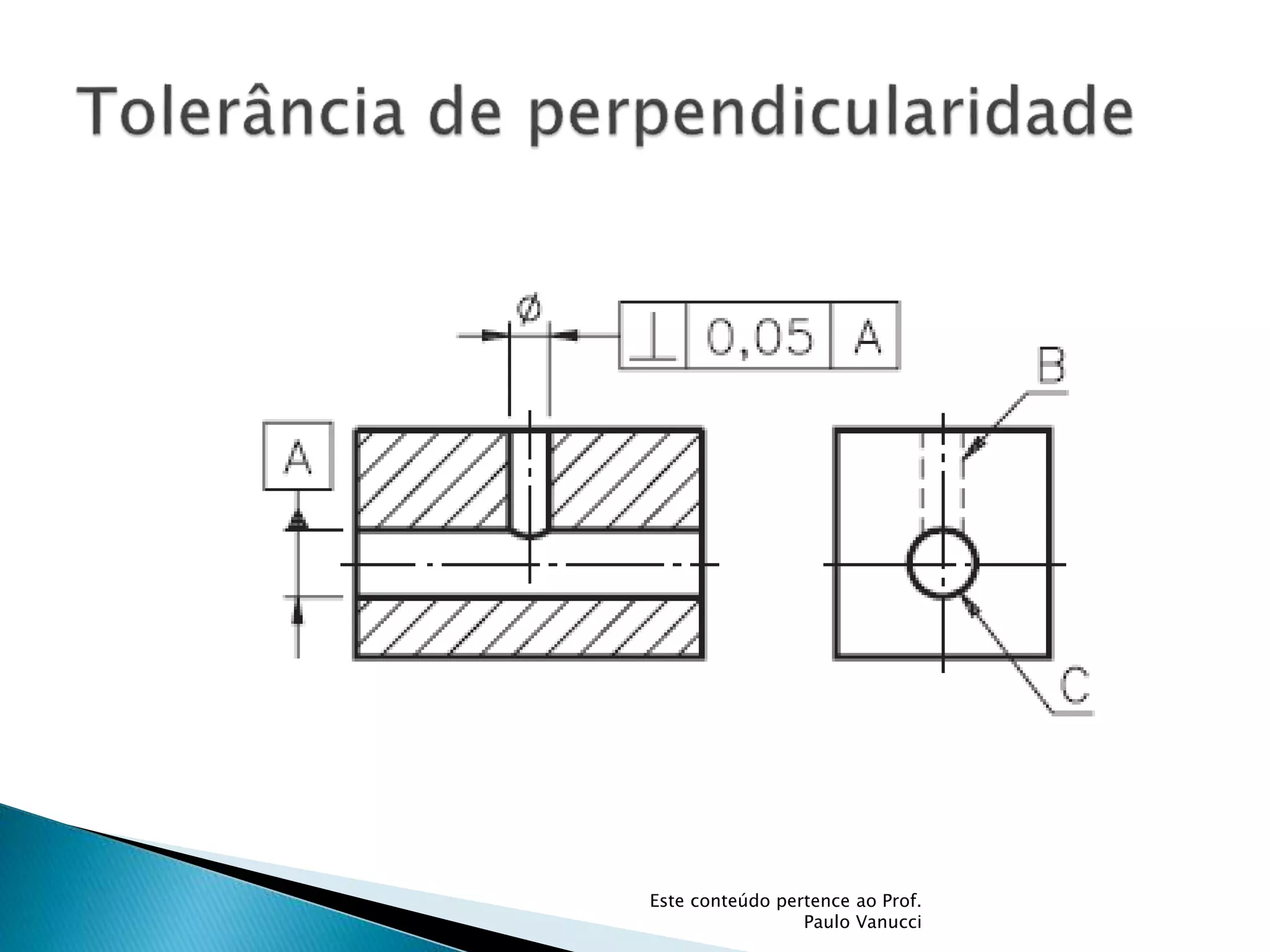
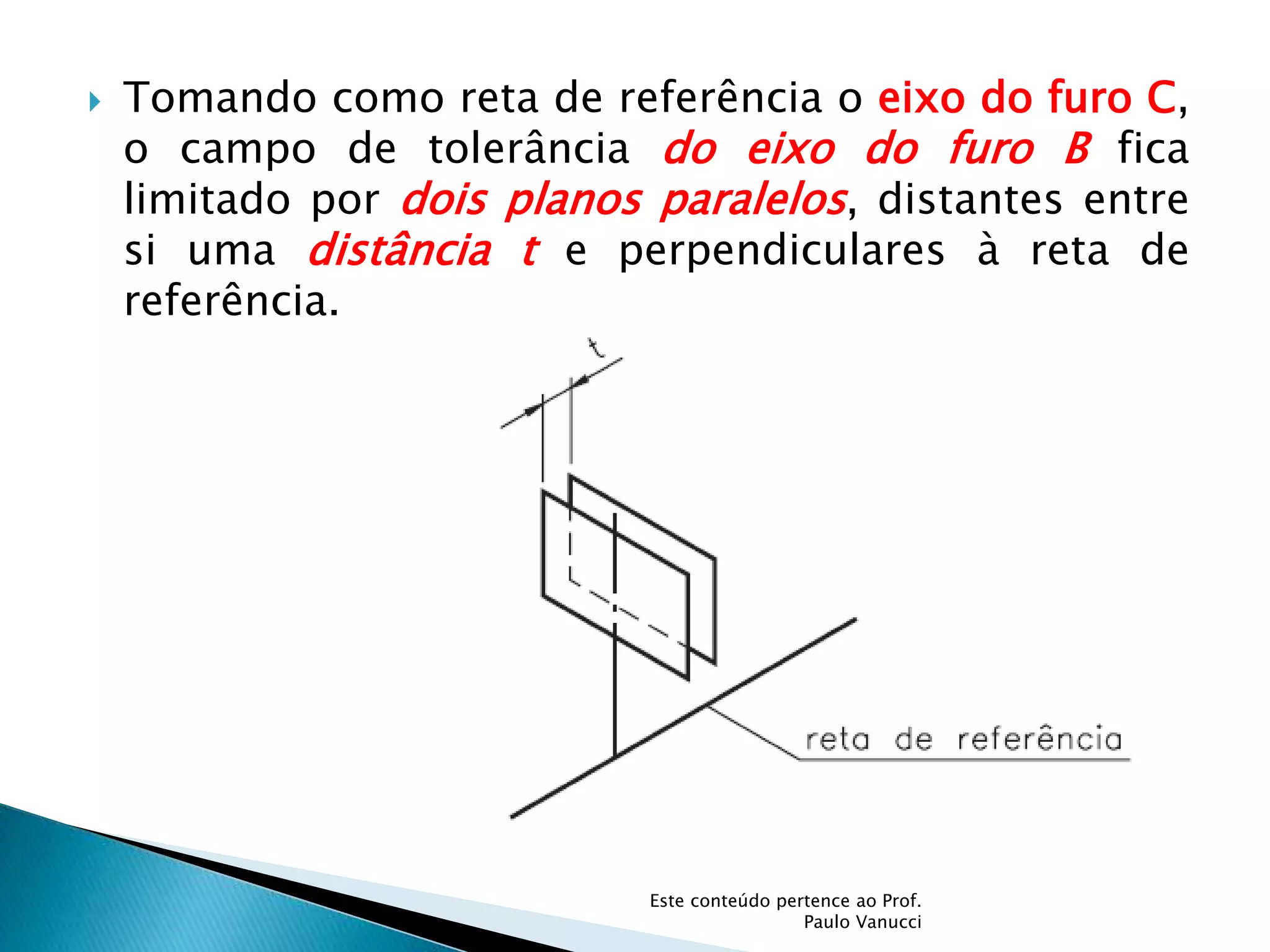
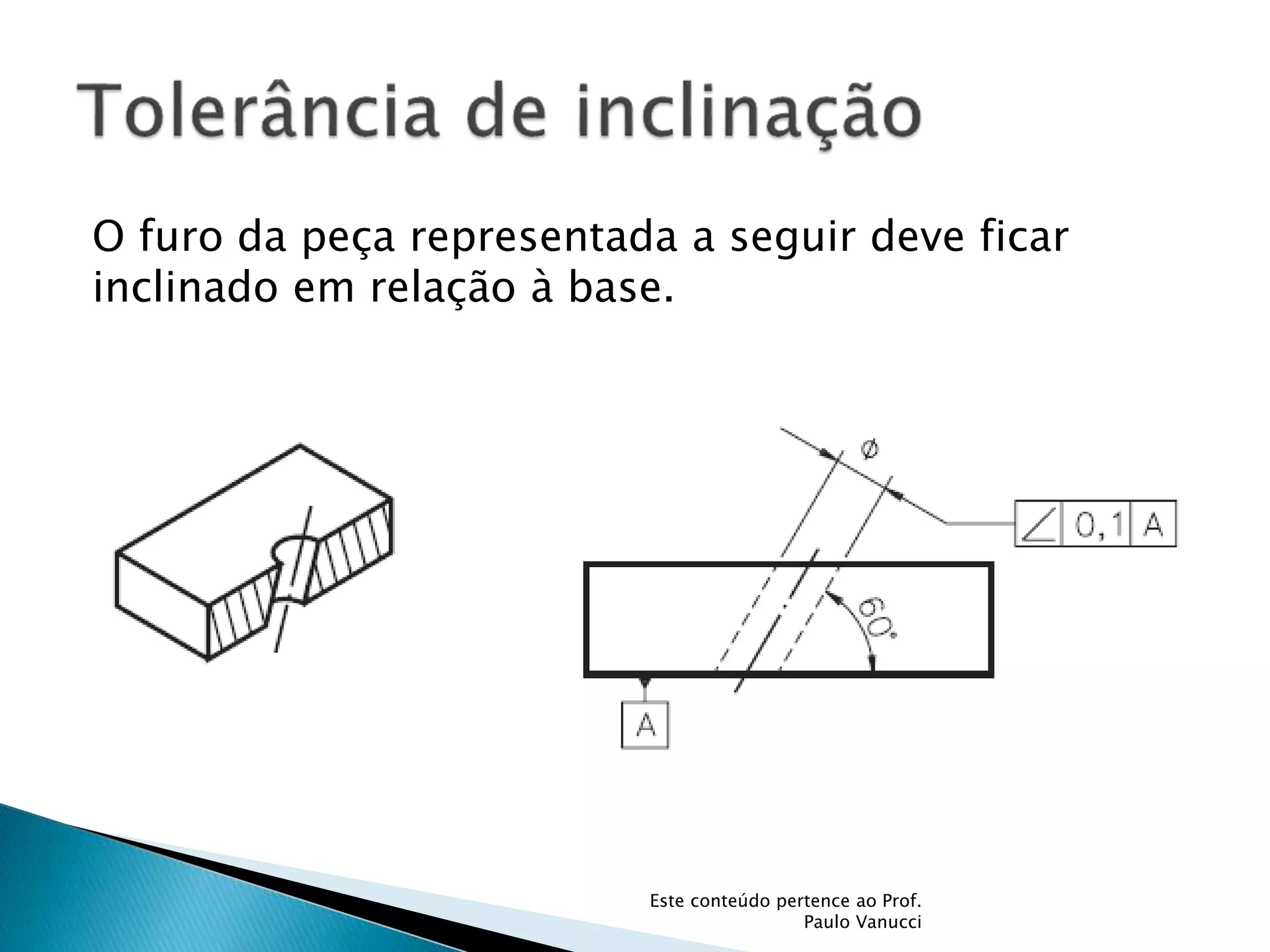
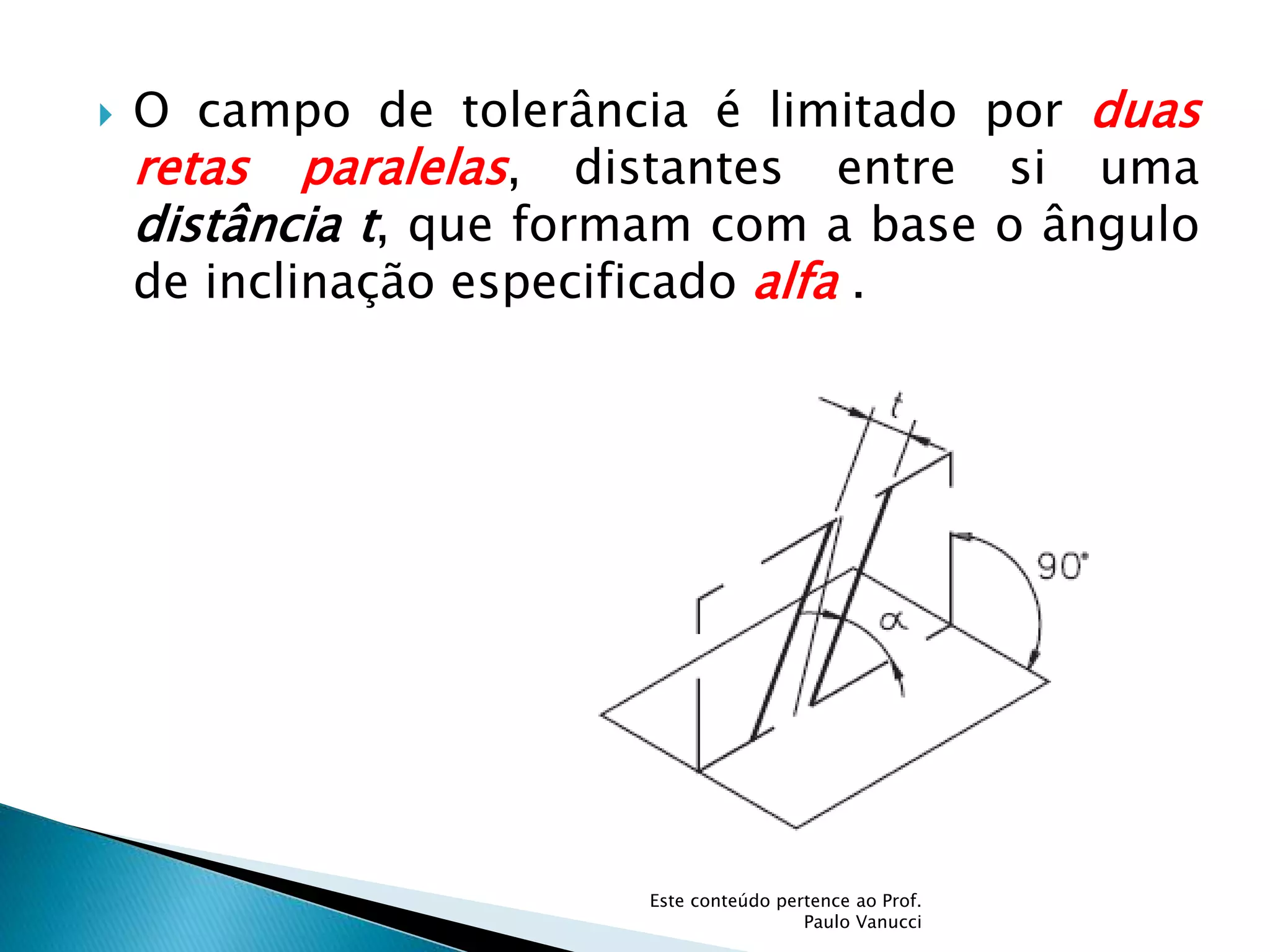
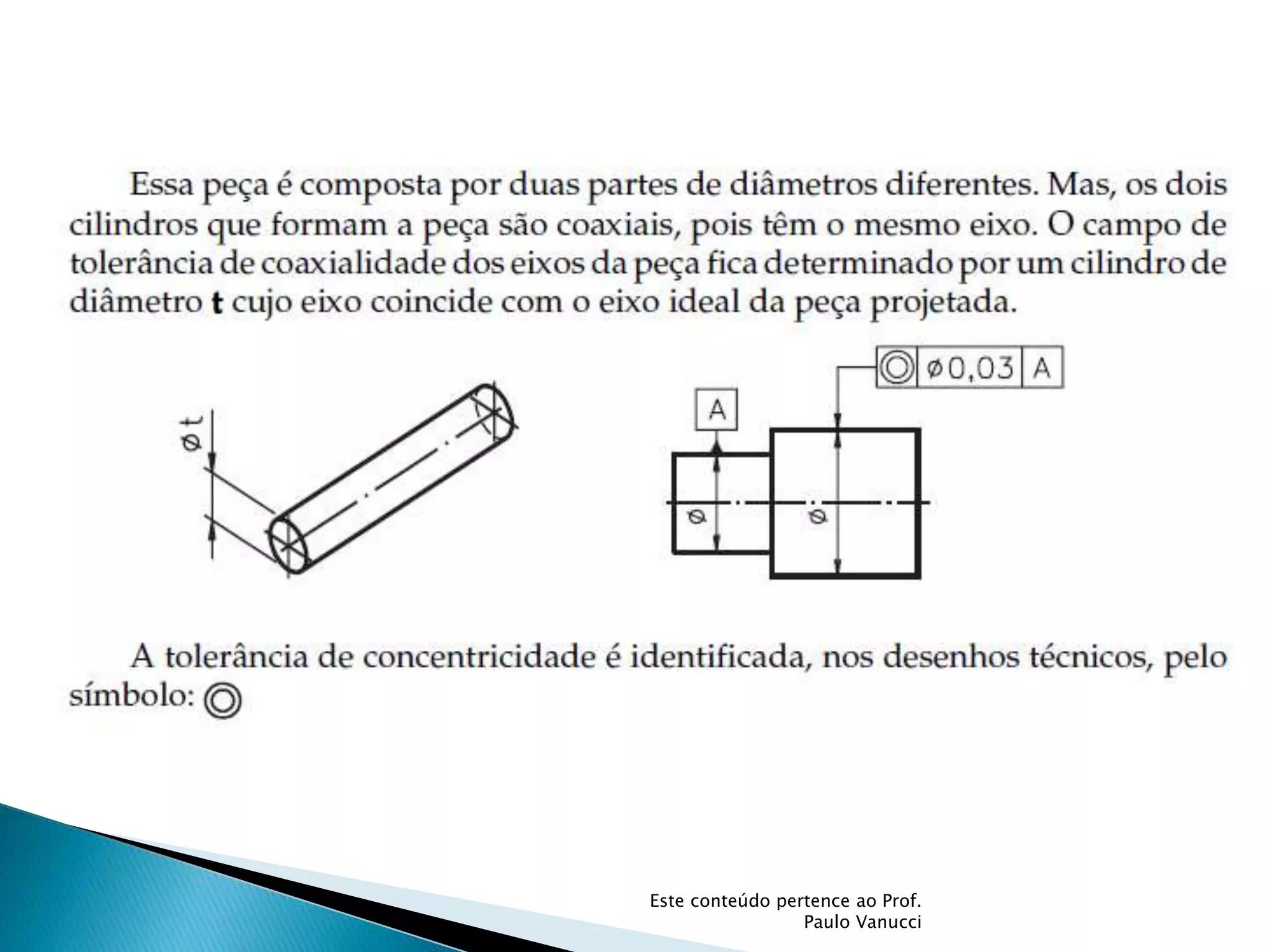
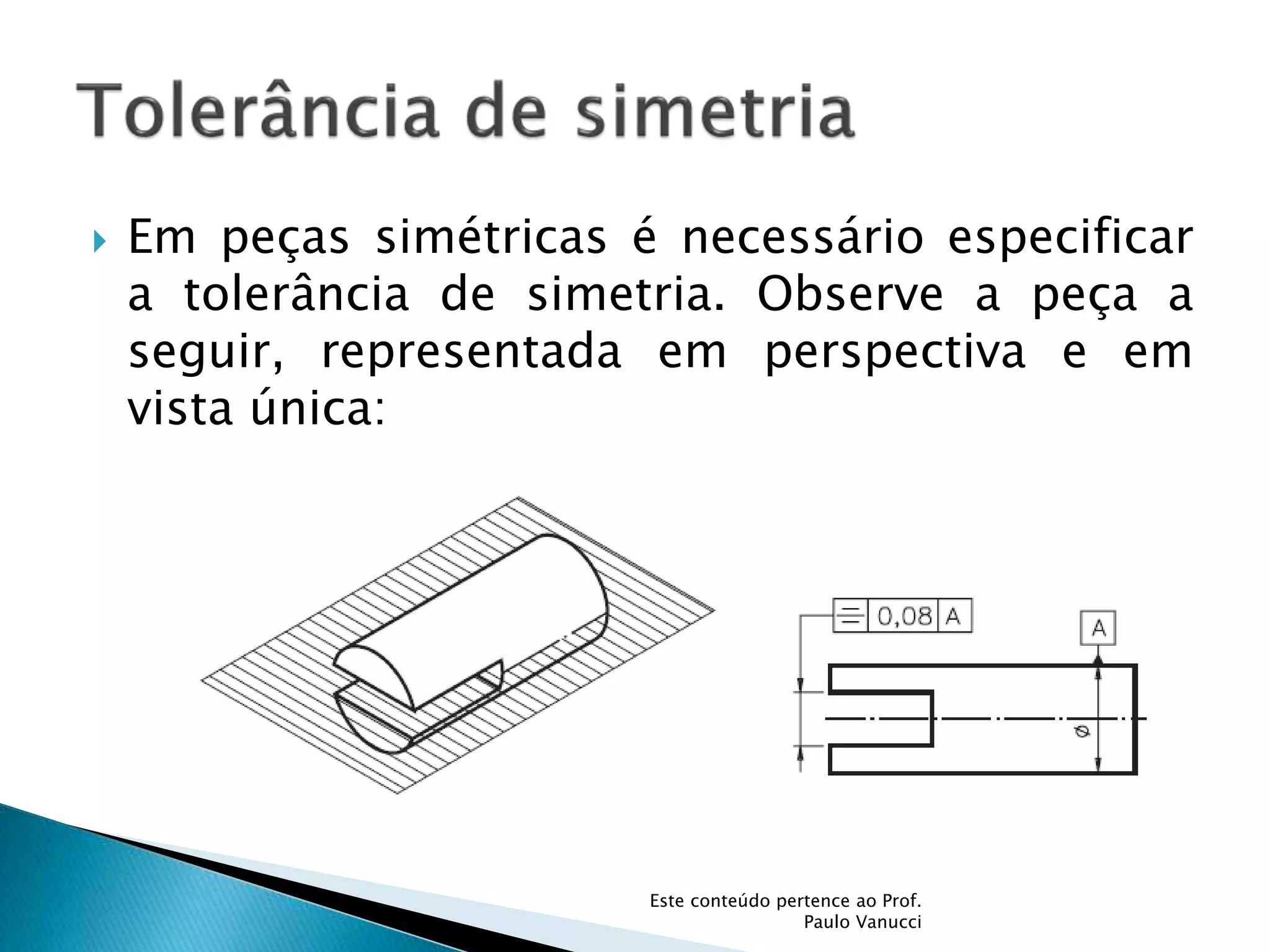
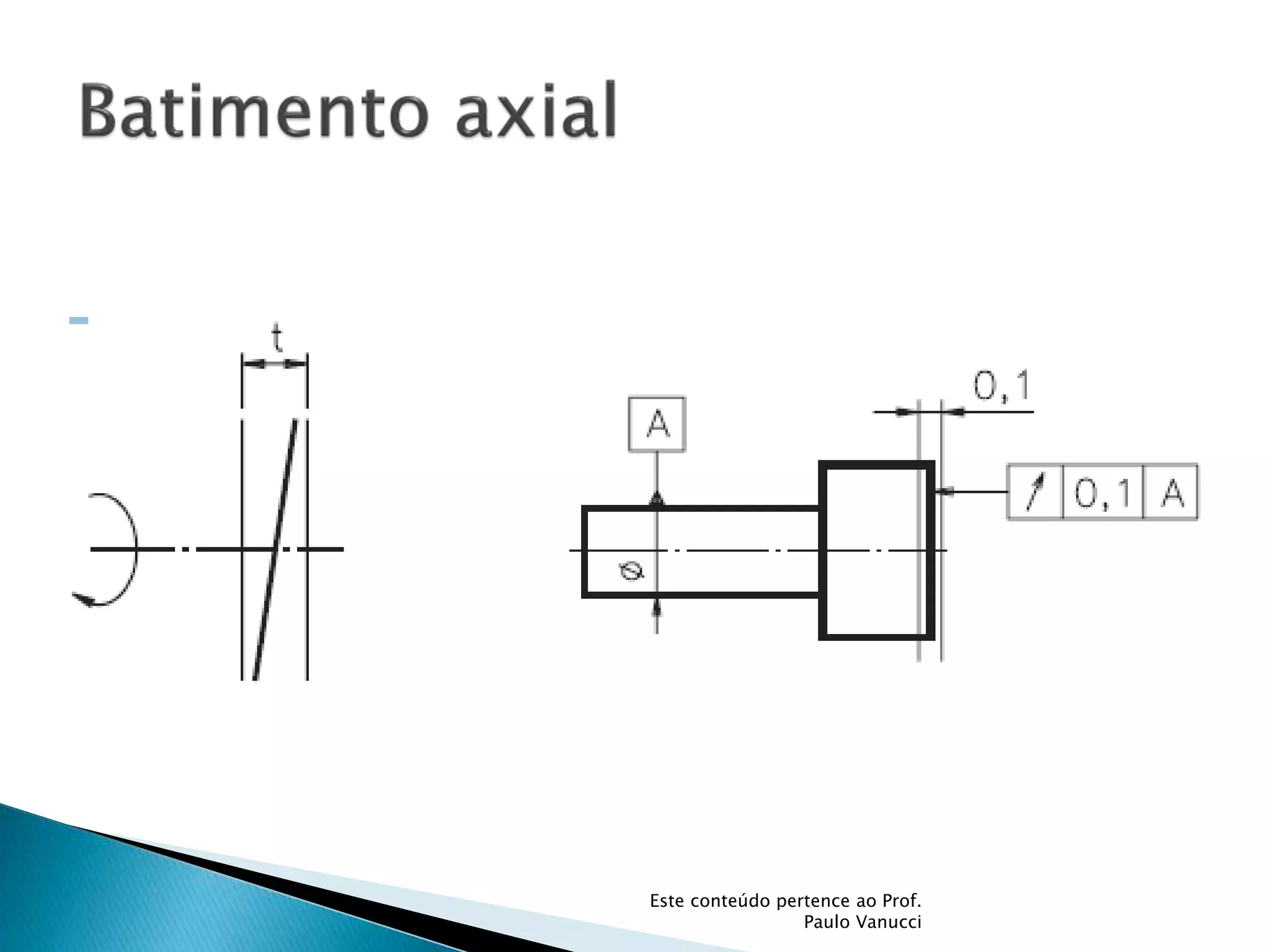
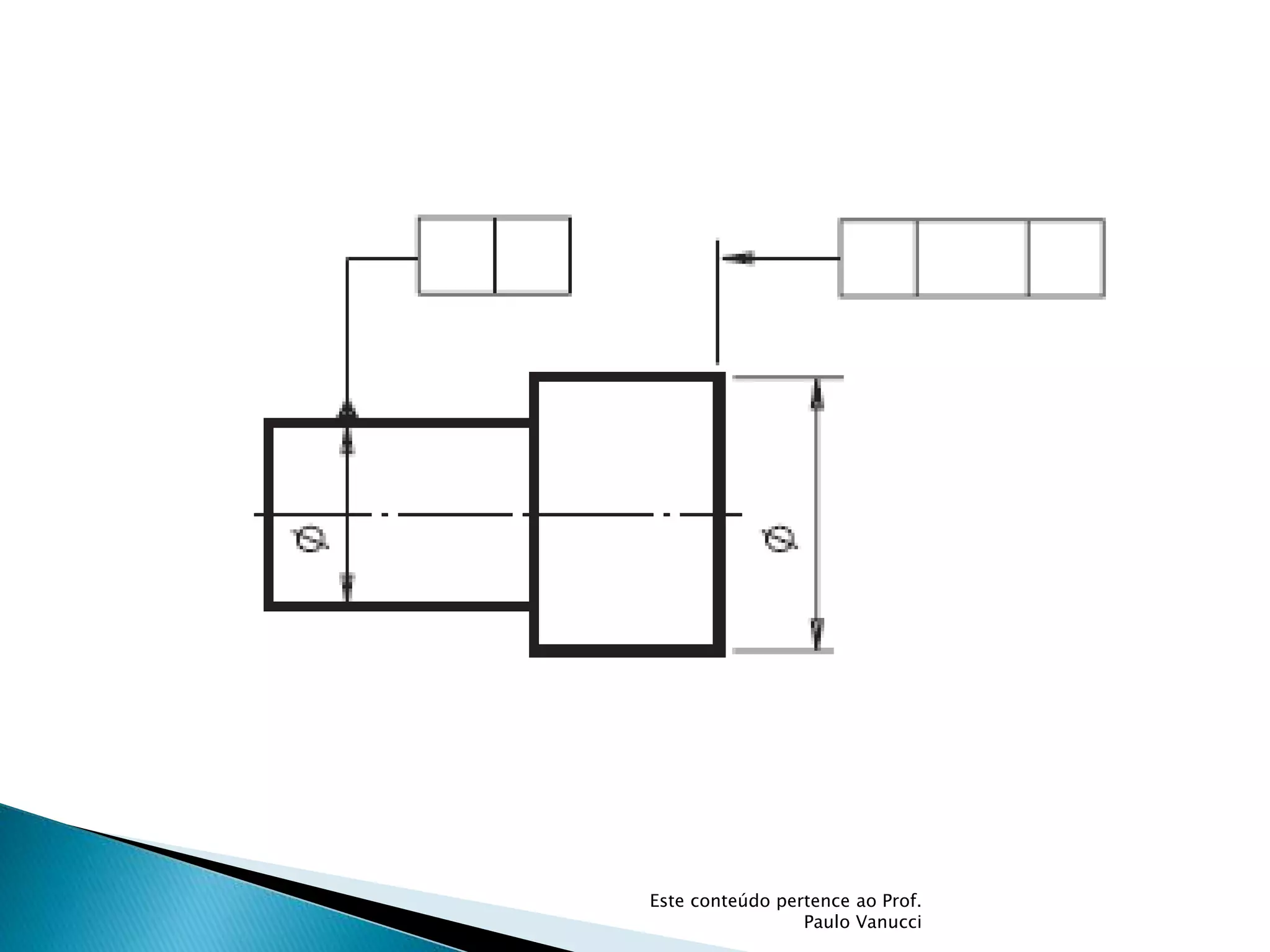
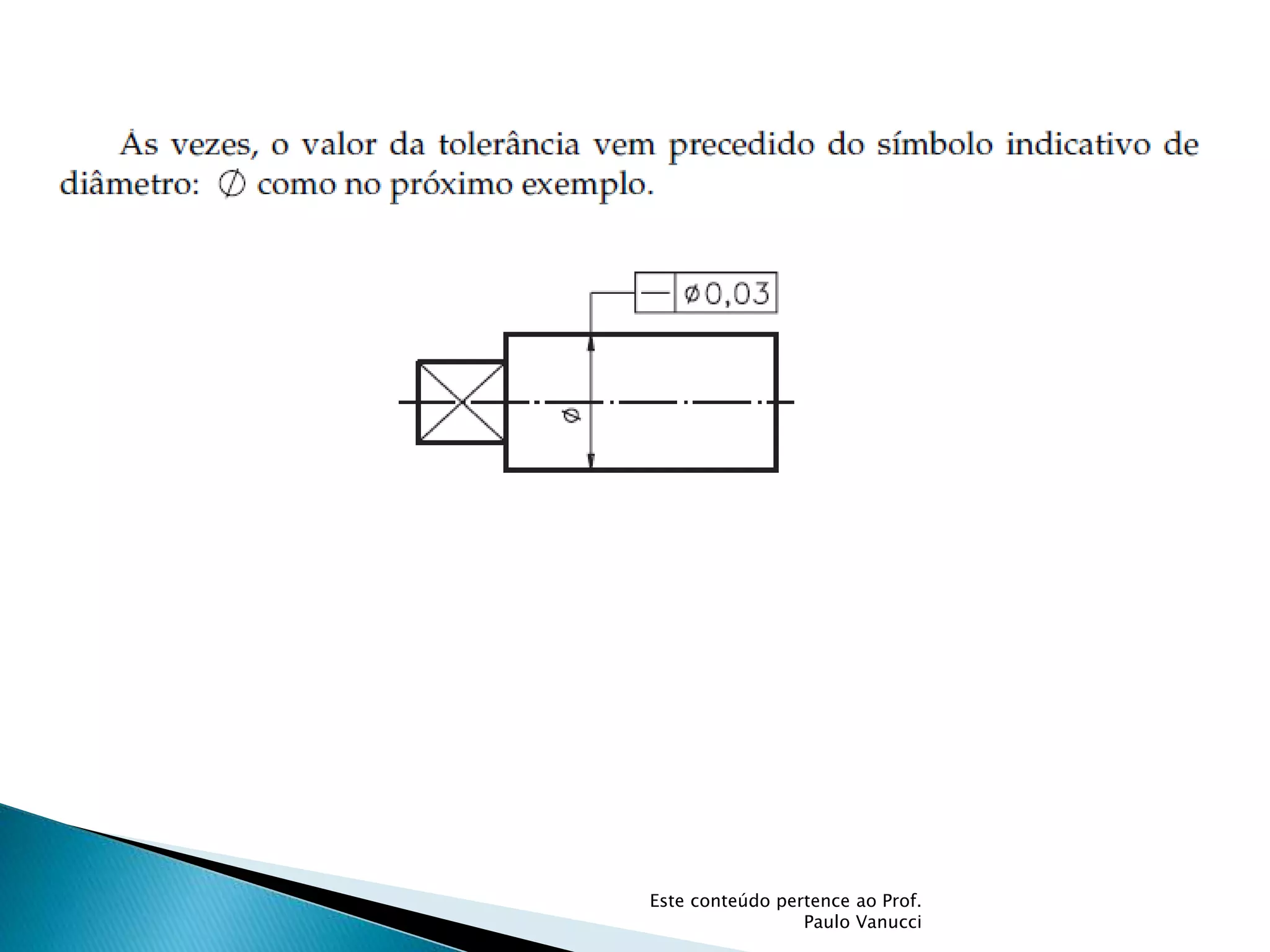
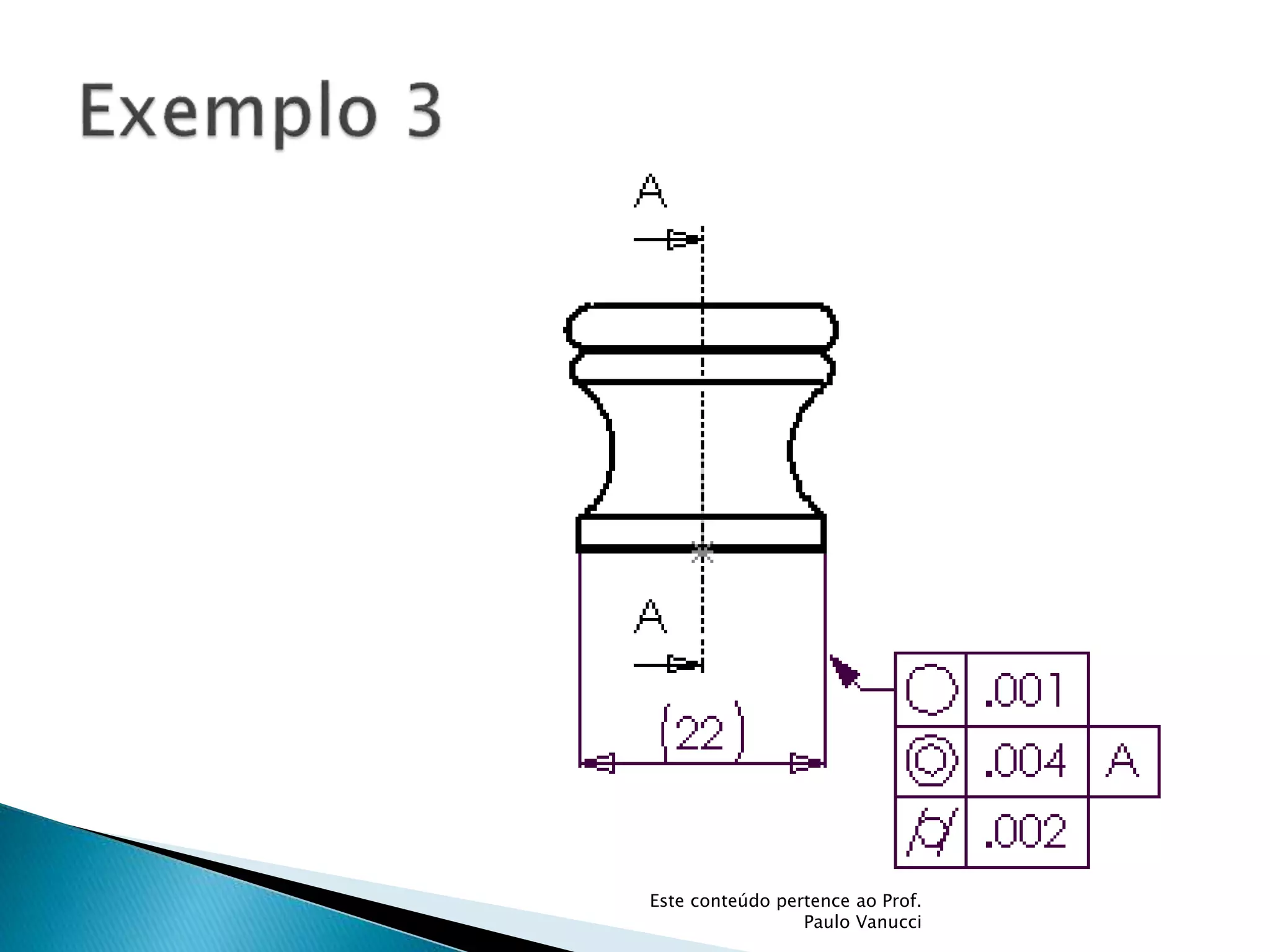
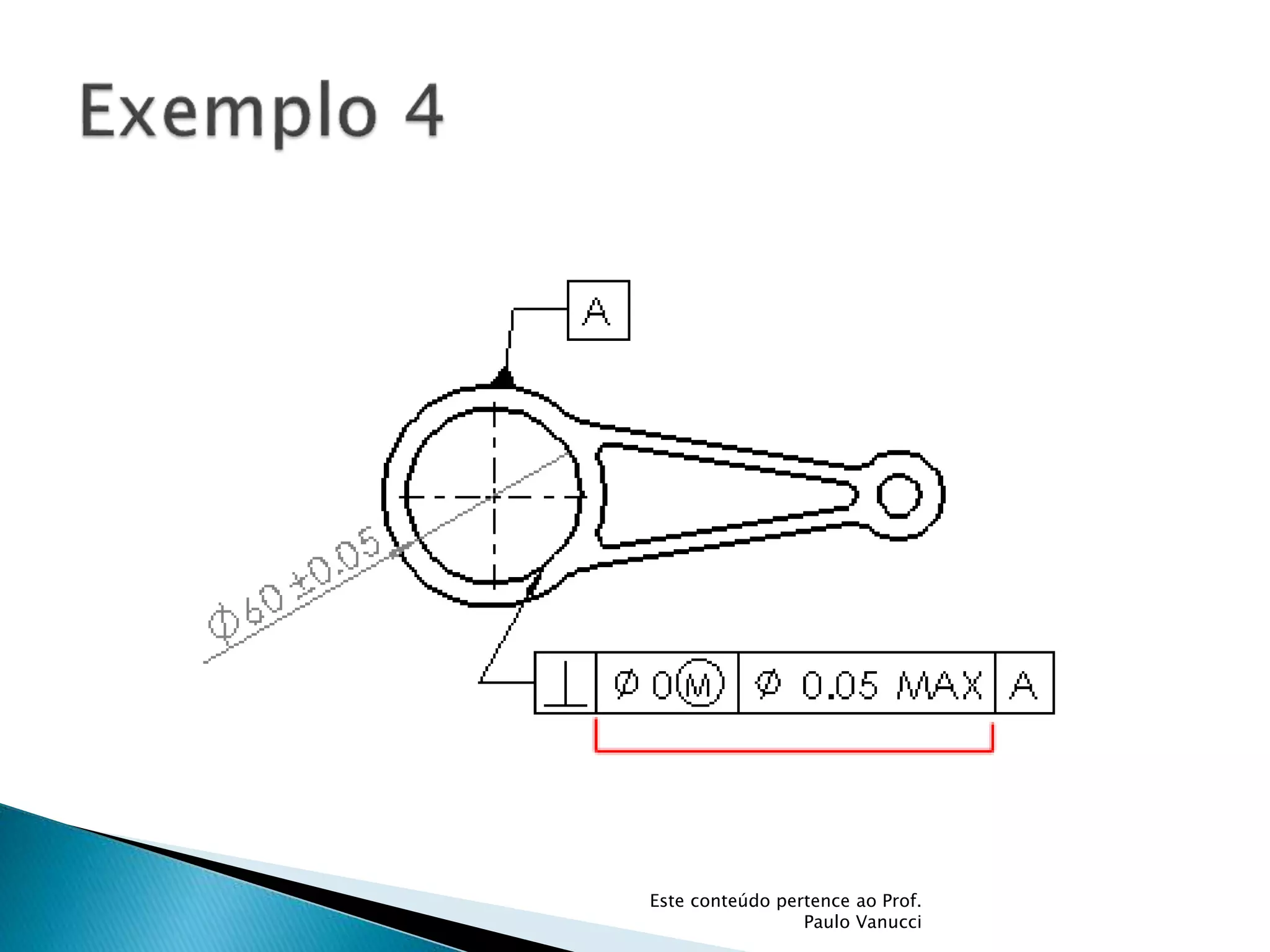
O documento discute os conceitos de tolerância dimensional e de forma em desenhos técnicos. Explica que as tolerâncias especificam os desvios permitidos nas dimensões e forma de peças em relação ao projeto ideal. Detalha os principais tipos de tolerâncias de forma, orientação e posição e como elas são indicadas graficamente nos desenhos.