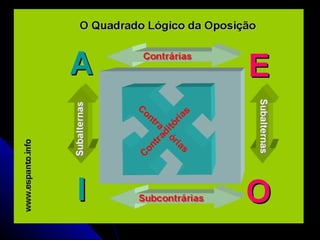
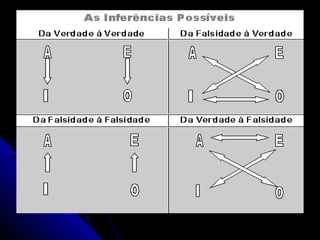
O documento discute o silogismo como uma forma de raciocínio lógico estruturado. Explica que Aristóteles estruturou o silogismo em termos de sujeito e predicado ligados pelo verbo "ser". Também descreve as partes do silogismo, regras de oposição e exemplos de silogismos.

1. Silogismo

3. Silogismo
 Cadapessoa tem uma forma especial de
pensar;
O senso comum e o pensamento informal
não dá segurança ao que é pensado;
O silogismo dá-nos a possibilidade de
garantir o argumento.

5. Padronização
O silogismo estrutura-se na padronização;
 Padronizar é estabelecer um modelo para
todos;
 Transformar toda frase em uma única
forma;
 Ex: a linguagem.
 Padronizar é traduzir uma proposição
comum na linguagem lógica.

6. Aristóteles
 Aristótelesresumiu os termos em dois:
sujeito e predicado;
 Numa proposição, o predicado está ligado
a um sujeito pelo verbo SER;
 Todos os verbos são dedutíveis do verbo
Ser;

7. Diamantes são pedras preciosas
Termo Termo Verbo Termo
Quantif. Sujeito Predicado
Todos Os São Pedras
diamantes preciosas
Nenhum Diamante é Pedra
preciosa
Alguns Diamantes São Pedras
preciosas
Alguns Diamantes Não são Pedras
preciosas

8. Exemplos
 Marcos constrói edifícios;
 Marcos é construtor de edifícios.
 Todos os homens trabalham nesse edifício;
 Todos os homens são trabalhadores deste
edifício.

9. Partes do silogismo
 Premissa maior: Todos os homens são
mortais;
 Premissa menor: Sócrates é homem.
 Conclusão: Sócrates é mortal

10. Letras = Termos
T – Termo maior = mortal;
M – Termo médio = homem;
t – Termo menor = Sócrates.

11. Termos
 Termo maior é o termo cuja extensão
envolve todos os outros termos;
 Termo menor é quando a extensão da
palavra é reduzida a um determinado
elemento;
 Termomédio faz a relação entre o maior
e o menor

13.  Regras da Oposição
 CONTRÁRIAS (A e E) Não
podem ser ambas verdadeiras, podendo ser
ambas falsas.
 CONTRADITÓRIAS(A e O; E e I) Não podem
ser ambas verdadeiras ou falsas ao mesmo
tempo, se uma é verdadeira, a outra é falsa, e
inversamente.
 SUBCONTRÁRIAS (I e O) Não podem ser
ambas falsas, podendo ser ambas verdadeiras.
 SUBALTERNAS (A e I; E e O) Se a universal for
verdadeira, a particular não pode ser falsa; Se a
particular for falsa, a universal não pode ser
verdadeira.

15.  Atividades:

 1. Dada a proposição A= “Todos os animais são seres vivos”:
 1.1 . Apresente as opostas de A.
 1.2. Sendo A verdadeira, indique o valor de verdade de cada
uma das suas opostas. Justifique.

 2. Se for falso que Nenhum homem é europeu, pode ser verdade
que Alguns homens são europeus? Justifique a sua resposta.

 3. Tendo as proposições: P= “Alguns australianos não gostam de
futebol” e Q= “Nenhum australiano gosta de futebol”:
 3.1. Se Q for falsa, P pode ser verdadeira? Justifique a sua
resposta.
 3.2. Apresente as contraditórias de P e de Q.
 3.3. Sendo P falsa, decida do valor de verdade das
contraditórias de P e de Q.

 4. Se demonstrar que Todos os corvos são negros, podemos
considerar que também fica demonstrado que Alguns corvos são
negros? Justifique a sua resposta.

16.  1. Dada a proposição A= “Todos os animais são seres vivos”:
 1.1 . Apresente as opostas de A.
 R: Contraditória: “Alguns animais não são seres vivos”.
 Subalterna: “Alguns animais são seres vivos”.
Subalterna: “Alguns animais são seres vivos”.
 Contrária: “Nenhum animal é ser vivo”.
Contrária: “Nenhum animal é ser vivo”.
 1.2. Sendo A verdadeira, indique o valor de verdade de cada uma das suas opostas. Justifique.
 R: Contraditória: Falsa. Porque de acordo com a regra das contraditórias, duas proposições
contraditórias não podem ser nem verdadeiras , nem falsas ao mesmo tempo, por isso se A é verdadeira,
a sua contraditória tem que ser falsa.
 2. Se for falso que Nenhum homem é europeu, pode ser verdade que Alguns homens são europeus? Justifique a
europeu, europeus?
sua resposta.
 R: Atendendo só à relação entre estas duas proposições, que são contraditórias, a falsidade duma
implica a verdade da outra (e inversamente), pelo que a falsidade da primeira, implica a verdade da
segunda.

 3. Tendo as proposições: P= “Alguns australianos não gostam de futebol” e Q= “Nenhum australiano gosta de
futebol”:
 3.1. Se Q for falsa, P pode ser verdadeira? Justifique a sua resposta.
 R: Sim. Porque se trata de duas proposições subalternas e, neste caso, a falsidade da universal não
implica a falsidade da particular, pelo que esta pode ser verdadeira.
 3.2. Apresente as contraditórias de P e de Q.
 R: Contraditória de P: “Todos os australianos gostam de futebol”.
 Contraditória de Q: “Alguns australianos gostam de futebol”.
 3.3. Sendo P falsa, decida do valor de verdade das contraditórias de P e de Q.
 R: Contraditória de P: Verdadeira. Porque, de acordo com a regra das contraditórias, se uma é
verdadeira, a outra é falsa e inversamente.
 Contraditória de Q: Verdadeira, porque a sua subalterna, que neste caso é universal, é verdadeira, pois,
Contraditória de Q: Verdadeira, porque a sua subalterna, que neste caso é universal, é verdadeira, pois,
de acordo com a regra das subalternas, a verdade da universal implica a verdade da particular.

 4. Se se demonstrar que Todos os corvos são negros, podemos considerar que também fica demonstrado que
negros,
Alguns corvos são negros? Justifique a sua resposta.
negros?
 R: Sim, pois se a universal for verdadeira, a particular não pode ser falsa, de a acordo com a regra das
subalternas.

