1. O documento resume conceitos de probabilidade e estatística, incluindo classificação de experiências, espaço amostral, classificação de acontecimentos e cálculo de probabilidades. 2. Também aborda sistemas de equações lineares, incluindo resolução gráfica e de problemas. 3. Outros tópicos incluem proporcionalidade, geometria, operações com potências e notação científica.

1. Resumos Intermédio Matemática Fevereiro
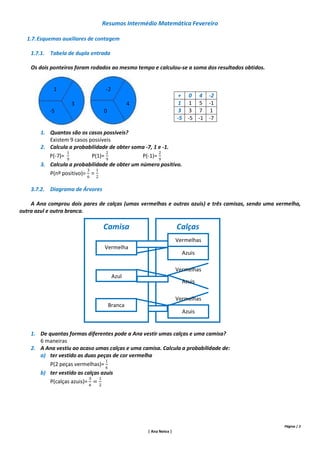
1. Probabilidades
1.1. Classificação de experiências
Experiência aleatória caracteriza-se pela impossibilidade de prever o resultado que se obtém, ainda que as
experiências sejam realizadas nas mesmas condições.
Ex. Tirar uma carta de um baralho; lançar um dado
Experiência determinista caracteriza-se por produzir o mesmo resultado desde que sejam repetidas nas mesmas
condições.
Ex. Empurrar uma caneta para fora do tampo da mesa; desligar a televisão da tomada
1.2. Conjunto de resultados
Ao conjunto de todos os resultados possíveis numa experiência aleatória chama-se espaço amostral ou espaço
de resultados. Representa-se por S.
Ex. Lançamento de um dado equilibrado
S= {1,2,3,4,5,6}
 sair número par S= {2,4,6]
 sair número menor que 7 S= {1,2,3,4,5,6}
 sair o 3 S= {3}
 sair o 8 S= { }
1.3. Classificação de acontecimentos
Acontecimento elementar só tem 1 elemento
Acontecimento composto tem 2 ou mais elementos
Acontecimento certo o seu conjunto de resultados é igual ao espaço amostral
Acontecimento impossível o seu conjunto de resultados é o conjunto vazio
Acontecimentos equiprováveis os seus conjuntos de resultados têm o mesmo número de elementos
1.4. Como varia a probabilidade?
0 1
Impossível Provável Certo
P (“sair número par”) =
1.5. Lei de Laplace
A probabilidade de um acontecimento A é o quociente entre o número de casos favoráveis e o número de casos
possíveis.
P(A) =
1.6. Propriedade de um acontecimento contrário
Probabilidade de um acontecimento contrário = 1 - Probabilidade de um acontecimento
Página | 1
| Ana Neiva |

2. Resumos Intermédio Matemática Fevereiro
1.7. Esquemas auxiliares de contagem
1.7.1. Tabela de dupla entrada
Os dois ponteiros foram rodados ao mesmo tempo e calculou-se a soma dos resultados obtidos.
1 -2
+ 0 4 -2
3 4 1 1 5 -1
-5 0 3 3 7 1
-5 -5 -1 -7
1. Quantos são os casos possíveis?
Existem 9 casos possíveis
2. Calcula a probabilidade de obter soma -7, 1 e -1.
P(-7)= P(1)= P(-1)=
3. Calcula a probabilidade de obter um número positivo.
P(nº positivo)=
3.7.2. Diagrama de Árvores
A Ana comprou dois pares de calças (umas vermelhas e outras azuis) e três camisas, sendo uma vermelha,
outra azul e outra branca.
Camisa Calças
Vermelhas
Vermelha
Azuis
Vermelhas
Azul
Azuis
Vermelhas
Branca
Azuis
1. De quantas formas diferentes pode a Ana vestir umas calças e uma camisa?
6 maneiras
2. A Ana vestiu ao acaso umas calças e uma camisa. Calcula a probabilidade de:
a) ter vestido as duas peças de cor vermelha
P(2 peças vermelhas)=
b) ter vestido as calças azuis
P(calças azuis)=
Página | 2
| Ana Neiva |

3. Resumos Intermédio Matemática Fevereiro
3.7.3. Diagrama
Numa escola de dança existem 50 alunos. Desses alunos, 25 praticam Ballet e 30 praticam jazz.
50
B BJ J
20 5J 25
20
Soma-se os alunos das duas modalidades. (é maior que o número de alunos)
30+25=55
Vê-se quantos sobram, ou seja, quantos praticam ambas as modalidades.
55-50=5 (número de alunos que praticam ambas as modalidades)
Tira-se esse número (neste caso 5) ao número de alunos de cada modalidade.
25-5=20 (número de alunos que praticam ballet)
30-5=25 (número de alunos que praticam jazz)
1. Qual a probabilidade de um aluno, escolhido ao acaso, praticar:
a) só ballet
P(só ballet)=
b) as duas modalidades
P(duas modalidades)=
c) pelo menos uma das modalidades
P(pelo menos uma modalidades)= 1
3.8. Lei dos Grandes Números
Em probabilidades, quando se repete uma experiencia aleatória um grande número de vezes, podemos dizer que
a frequência relativa de um acontecimento se aproxima da probabilidade desse acontecimento.
3.9. Frequência Relativa
2. Sistemas de Equações
2.1. Como fazer um sistema?
1. Resolve-se uma das equações em ordem a uma das incógnitas
2. Substitui-se a expressão obtida na outra equação
3. Resolve-se esta equação
4. Substitui-se o valor obtido da incógnita na outra equação e encontra-se o valor da outra incógnita
Sistemas equivalentes são aqueles que admitem as mesmas soluções.
Página | 3
| Ana Neiva |

4. Resumos Intermédio Matemática Fevereiro
2.2. Classificação de sistemas
Sistema Possível Determinado admite uma só solução (um único par ordenado verifica as duas equações
simultaneamente).
Sistema Possível Indeterminado admite uma infinidade de soluções (quando se obtém uma condição universal;
as duas equações transmitem a mesma informação – são equivalentes).
Sistema Impossível não admite nenhuma solução (quando se obtém uma condição impossível); não há soluções
simultâneas para as duas equações.
2.3. Resolução Gráfica de Sistemas
Cada uma das equações de um sistema pode ser representada graficamente por uma recta. Os pontos de
intersecção das duas rectas são as soluções do sistema. Assim:
 Se as rectas se intersectam apenas num ponto, há apenas uma solução; o sistema é possível determinado.
 Se as rectas coincidem, há uma infinidade de soluções; o sistema é possível indeterminado.
 Se as rectas não se intersectam, não há soluções; o sistema é impossível.
2.4. Resolução de Problemas
Tal como as equações, os sistemas são uma ferramenta fundamental para resolver alguns tipos de problemas.
Quando temos duas incógnitas, devemos procurar encontrar duas equações para resolver o problema
Guião para a resolução de problemas:
 Compreender o problema
 Identificar a incógnita
 Traduzir o problema por meio de um sistema
 Resolver o sistema
 Verificar se a solução do sistema serve como solução do problema
 Dar resposta ao problema
3. Proporcionalidade inversa vs Proporcionalidade directa
Proporcionalidade Directa Proporcionalidade Inversa
O quociente entre os valores correspondentes das duas O produto dos valores correspondentes das duas
variáveis é constante. variáveis é constante.
x1 x2 x3 x1 x2 x3
y1 y2 y3 y1 y2 y3
Expressão analítica Expressão analítica
Constante k Constante k
O gráfico é constituído por pontos que se situam sobre
O gráfico é uma hipérbole.
uma recta que passa na origem do sistema de eixos.
Página | 4
| Ana Neiva |

5. Resumos Intermédio Matemática Fevereiro
4. Geometria
4.1. Construção de triângulos
Para se poder construir um triângulo, a soma dos dois lados mais pequenos tem de ser maior que o terceiro lado.
Ex.: 5cm, 7cm e 9cm (5 + 7 = 12 > 9)
4.2. Semelhança de triângulos
 2 ângulos iguais
 3 lados directamente proporcionais
 2 lados proporcionais e o ângulo por eles formado igual
4.3. Razão de semelhança
 a razão entre perímetros é a razão de semelhança
 a razão entre áreas é a razão de semelhança ao quadrado
5. Regras operatórias das potências
5.1. Multiplicação
 Mesma base, somam-se os expoentes
am x an = am+n
 Mesmo expoente, multiplicam-se as bases
an x bn = (ab)n
5.2. Divisão
 Mesma base, subtraem-se os expoentes
am : an = am-n
 Mesmo expoente, dividem-se as bases
an : bn = (a:b)n
5.3. Potência de potência
 Numa potência de potência, multiplicam-se os expoentes
[(a)n]m = amxn
5.4. Expoente negativo
 Com expoente negativo, troca-se o numerador com o denominador
Página | 5
| Ana Neiva |

6. Resumos Intermédio Matemática Fevereiro
6. Notação científica
6.1. Colocar em notação científica
 Número = Número entre 0 e 9 x 10(elevado ao número de casas que andou)
3100 = 3,1 x 103 0,0003 = 3 x 10-4
6.2. Operações em notação científica
6.2.1. Adição e subtracção 6.2.2. Multiplicação e divisão
0,5 x 1011 + 22,4 x 108 = 5,06 x 10-17 x 4,5 x 1013 =
= 0,5 x 103 x 108 + 22,4 x 108 = = (5,06 x 4,5) x (10-17 x 1013) =
= (500 + 22,4) x 108 = = 22,77 x 10-4 =
= 522,4 x 108 = = 2,277 x 10-3
= 5,224 x 1010
Página | 6
| Ana Neiva |