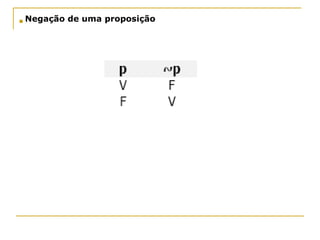
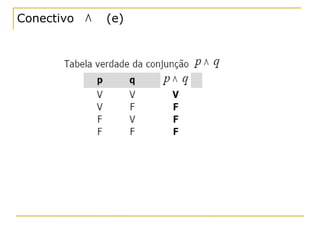
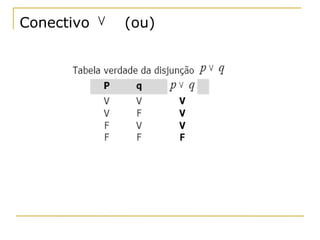
O documento apresenta os principais conceitos de lógica proposicional, incluindo proposições, negação, conectivos lógicos como conjunção, disjunção e condicional. Explica como determinar o valor lógico de frases compostas e como construir tabelas-verdade. Também aborda quantificadores universais e existenciais e como negar proposições quantificadas.

1. MATEMÁTICA_2
PROF. MIGUEL

2. Noções básicas de lógica
 Proposição
Proposição é toda oração declarativa, com sentido
completo, podendo ser classificada como
Verdadeira (V) ou Falsa (F).

3.  Princípio da não contradição.
 Princípio do terceiro excluído.
Proposição simples
Ex.: Matemática é uma disciplina legal.
 Proposição composta
Ex.: Matemática é uma disciplina legal e
o professor é exigente.

4.  Negação de uma proposição

5. Exemplos
a) p: Jorge é alto.
~p: Jorge não é alto.
b) q: ≥ 12.
25
~q: < 12.
25

6. Conectivo ∧ (e)
∧

7. Determinar o valor lógico das frases
a) A gaivota voa e o ornitorrinco é ave.
b) O avestruz não voa e não bota ovos.
c)A vaca é bípede e o cachorro late.

8. Conectivo ∨ (ou)

9. Determinar o valor lógico das frases
a) A gaivota voa ou o ornitorrinco é ave.
b) O avestruz não voa ou não bota ovos.
c)A vaca é bípede ou o cachorro late.

10. Condicional → (se...então)

11. Entendo melhor a tabela verdade do
condicional →
Considera situação: Joãozinho faz uma
“promessa” a Mariazinha:
_ Se você for corinthiana então você ganhará
um presente.
Quais são os eventos possíveis?
Admitamos que aquilo que obedece à
“promessa”, tenha valor lógico V e aquilo
que não obedece valor lógico F.

12. 1) Mariazinha é corinthiana e ganhou presente.
2) Mariazinha é corinthiana e não ganhou
presente.
3) Mariazinha não é corinthiana e ganhou
presente.
4) Mariazinha não é corinthiana e nãoganhou
presente.
Em qual(quais) opções a “promessa” foi
cumprida?

13. (Bi)Condicional ↔ (... se, e somente
se ...)

14. Entendo melhor a tabela verdade do
condicional ↔
Situação
Professor diz aos alunos:
_“Você receberá F.O.+ se, e somente se, fizer a
tarefa.”
1) Recebeu F.O.+ e fez a tarefa.
2) Recebeu F.O.+ e não fez a tarefa.
3) Não recebeu F.O.+ e fez a tarefa.
4) Não recebeu F.O.+ e não fez a tarefa.

15. Implicação lógica ⇒
Usamos implicação lógica quando o condicional
→ (se... então ...) tiver valor lógico
verdadeiro.

16. Equivalência lógica ⇔
Usamos equivalência lógica quando o
(bi)condicional ↔ (... Se, e somente
se, ...) tiver valor lógico verdadeiro.
Também usamos equivalência lógica quando as
tabelas-verdades são iguais.

17. Sentença aberta
Sentença em que o valor lógico (V ou F)
depende de alguma informação
(variável).
Ex.: x+2=13.

18. Existem duas formas de transformar
sentenças abertas em proposições:
 Atribuir valor às variáveis.
 Utilizar quantificadores.

19. Quantificador Universal ∀
É indicado pelo símbolo ∀ que se lê:
“qualquer que seja”, “para todo”.

20. Quantificador Existencial ∃
É indicado pelo símbolo ∃ que se lê: “existe”,
“existe pelo menos um”.
É também utilizado outro quantificador ∃ | que
se lê: “existe um único”.

21. Construindo tabela-verdade

24. Negando uma conjunção
Podemos verificar, em (A), que
~ ( p ∧ q ) ⇔ (~ p ) ∨ (~ q ) , assim
sendo a negação da proposição p ∧ q
é a proposição (~ p ) ∨ (~ q ) .

25. Negação de uma disjunção
Podemos verificar, em (B), que
~ ( p ∨ q ) ⇔ (~ p ) ∧ (~ q ) ,
assim sendo, a negação da proposição
p∨ q é a proposição ) ∧ (~ q )
(~ p
.

26. Negação de um condicional
simples
Podemos verificar, em (C), que
~ ( p → q) ⇔ ( p ∧ ~ q) , assim
sendo, a negação da proposição p → q
é a proposição ( p∧ ~ q ) .

27. Negação de proposições
quantificadas
Uma sentença quantificada com o
quantificador universal,
do tipo (∀ x )( p ( x )) , é negada assim:
substitui-se o quantificador universal pelo
existencial e nega-se p ( x ) obtendo:
(∃ x )(~ p ( x ))

28. Uma sentença quantificada com o
quantificador existencial,
do tipo (∃ x )( p ( x )) é negada assim:
substitui-se o quantificador existencial
pelo universal e nega-se p ( x ) obtendo:
(∀ x )(~ p ( x ))