Unidade 3 cap 1.2 (a)

Lógica proposicional clássica
= disciplina da Lógica iniciada pelos estóicos (Grécia, séc. III a.C.)
e desenvolvida no séc. XX.
Proposição
= pensamento expresso numa frase declarativa com sentido
Variável proposicional
= símbolo que representa uma proposição
(consoantes maiúsculas a partir do P)
Forma proposicional
= estrutura da proposição (sem qualquer conteúdo)
As variáveis proposicionais surgem nas formas proposicionais

Proposição
Simples = não tem qualquer operador
Composta = tem algum operador
Operador proposicional
= expressão que acrescentada a uma ou a duas proposições (simples ou compostas)
forma uma nova proposição
Ex. 1
Operador proposicional: “Toda a gente sabe que”. Frase: “Cinco é um número primo”
Nova frase: “Toda a gente sabe que cinco é um número primo”
Ex. 2
Operador proposicional: “e”. Frases: “Sábado vou sair”, “Sábado vou divertir-me”.
Nova frase: “Sábado vou sair e [sábado vou] divertir-me”

Operador [proposicional] verofuncional
= aquele que faz com que
[sabendo-se] o valor de verdade da(s) proposição(ões) sem ele
determine / [sabe-se]
o valor de verdade da proposição com ele
Ex. 1
operador não verofuncional:
“O Asdrúbal gostaria que”
Existe justiça social
F
O Asdrúbal gostaria que existisse justiça social
?
Operadores
Unários = aplicam-se a uma proposição
Binários = aplicam-se a duas proposições

Ex. 2
Operador verofuncional:
“É falso que” ou “não”
É falso que Matosinhos fique a sul do Douro
V
Matosinhos fica a sul do rio Douro
F
Matosinhos não fica a sul do Douro
V
No caso do operador verofuncional “É falso que” ou “não”
a sua colocação inverte o valor de verdade da proposição primitiva

Ex. 3
“e”
O Pedro é estudante da ESAG e mora em Lavra
F
O Pedro é estudante da ESAG
V
O Pedro mora em Lavra
F
No caso do operador verofuncional “e”
basta que uma das proposições intervenientes seja falsa
para que a formada por elas ligadas pelo operador seja falsa

Ex. 4
“ou”
A Luísa foi para a escola ou passear
V
A Luísa foi para a escola
V
A Luísa foi passear
F
No caso do operador verofuncional “ou”
basta que uma das proposições intervenientes seja verdadeira
para que a formada por elas ligadas pelo operador seja verdadeira

Tabelas de Verdade
Tabela de verdade
= dispositivo gráfico
que exibe os valores de verdade de uma forma proposicional
em cada uma das condições de verdade
Condições de verdade
= circunstâncias que tornam uma proposição verdadeira ou falsa
Ex. 1
“Três é um número par”
Circunstâncias possíveis: I – três ser um número par. II – três não ser um número par.
Na circunstância I a frase é verdadeira e na circunstância II a frase é falsa.

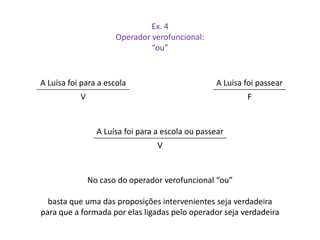
Ex. 2
“O Xico caminha gingão e [o Xico] mastiga chiclete.”
Existem quatro circunstâncias possíveis:
I – O Xico caminhar gingão (V) e mastigar chiclete (V).
II – O Xico caminhar gingão (V) e não mastigar chiclete (F).
III – O Xico não caminhar gingão (F) e mastigar chiclete (V).
IV – O Xico não caminhar gingão (F) e não mastigar chiclete (F).
Valor de verdade da frase citada em cada uma das circunstâncias:
• na circunstância I, a frase é V
• na circunstância II, a frase é F
• na circunstância III, a frase é F
• na circunstância IV, a frase é F
OBS:
Com outro operador verofuncional, por exemplo “ou” em lugar de “e”,
os resultados seriam diferentes (só na circunstância IV é que a frase citada seria F)

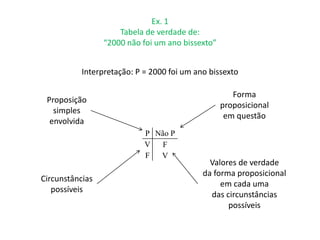
Ex. 1
Tabela de verdade de:
“2000 não foi um ano bissexto”
Interpretação: P = 2000 foi um ano bissexto
P Não P
V F
F V
Proposição
simples
envolvida
Circunstâncias
possíveis
Forma
proposicional
em questão
Valores de verdade
da forma proposicional
em cada uma
das circunstâncias
possíveis

Exs. 2 e 3
Tabelas de verdade de:
“No sábado fico em casa e leio um livro”
e de
“No sábado fico em casa ou leio um livro”
Interpretação: P = No sábado fico em casa. Q = No sábado leio um livro.
P Q P e Q
V V V
V F F
F V F
F F F
P Q P ou Q
V V V
V F V
F V V
F F F
OBS:
A tabela de verdade não diz se a proposição é V ou F,
diz em que circunstâncias a proposição é V ou F.

A
Quantas linhas tem uma tabela de verdade?
2n
Lógica bivalente:
2
valores de verdade
(V e F)
Número
de
variáveis
Exemplos:
Uma variável proposicional (P): 2 linhas. Duas variáveis proposicionais (P e Q): 4 linhas.
Três variáveis proposicionais (P, Q e R): 8 linhas...
B
Quantas colunas tem uma tabela de verdade?
À esquerda: uma coluna em baixo de cada variável proposicional
À direita: uma coluna em baixo de cada operador

C
Como se ordenam as linhas?
Na tabela de verdade têm de estar representadas todas as circunstâncias possíveis
A completude da tabela de verdade garante-se com uma convenção: à esquerda...
1.º
... colocam-se as variáveis proposicionais por ordem alfabética (P, Q, R, ...)
2.º
... e debaixo da:
última (por exemplo R) intercalam-se V e F um a um (VF),
penúltima (por exemplo Q) intercalam-se V e F dois a dois (VVFF),
antepenúltima (por exemplo P) intercalam-se V e F quatro a quatro (VVVVFFFF),
etc.

Disjunção [inclusiva] – operação lógica e designação da proposição composta
Proposições
intervenientes
Linguagem natural
(frases + operador)
Formalização
(variáveis proposicionais
+ constante lógica)
Disjuntas
No Homem existe livre-arbítrio
ou determinismo
P∨Q
P Q P ∨ Q
V V V
V F V
F V V
F F F
Regra:
A disjunção [inclusiva] é falsa quando ambas as disjuntas são falsas

Disjunção Exclusiva – operação lógica e designação da proposição composta
Proposições
intervenientes
Linguagem natural
(frases + operador)
Formalização
Disjuntas
Os dias do mês são
ou pares ou ímpares
P∨Q
P Q P ∨ Q
V V F
V F V
F V V
F F F
Regra:
A disjunção exclusiva é verdadeira (falsa)
se as disjuntas tiverem valores de verdade diferentes (iguais).

OBS:
“Inclusiva” se inclui a hipótese de ambas as disjuntas serem verdadeiras
“Exclusiva” se exclui essa hipótese
“Ou” / “ou... ou...”
não garante a distinção que tem de se fazer intuitivamente em função do contexto
Em Filosofia usa-se sobretudo a disjunção inclusiva.
Variantes:
O aluno é rapaz a menos que que seja rapariga
O dia do mês é par a não ser que seja ímpar

Conjunção – operação lógica e designação da proposição composta
Proposições
intervenientes
Linguagem natural
(frases + operador)
Formalização
Conjuntas
O Porto é uma cidade
nortenha e litoral
P∧Q
P Q P ∧ Q
V V V
V F F
F V F
F F F
Regra:
A conjunção é verdadeira quando ambas as conjuntas são verdadeiras

Variantes:
Tanto a conjunção quanto / como a disjunção são operações lógicas
Quer o vermelho quer o verde são cores nacionais
Portugal bem como / tal como a Espanha são países ibéricos
Agosto foi quente mas / apesar de / embora / no entanto ventoso
Nota:
A lógica é indiferente a qualquer expressividade...

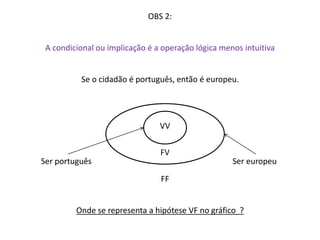
Condicional ou Implicação – operação lógica e designação da proposição composta
Proposições
intervenientes
Linguagem natural
(frases + operador)
Formalização
Antecedente e
Consequente
Se o individuo é
português, [então o
individuo] é europeu.
Um individuo ser
português implica que
seja europeu.
PQ
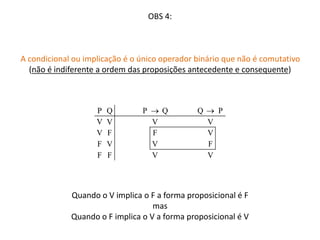
P Q P  Q
V V V
V F F
F V V
F F V
Regra:
A condicional é falsa quando a verdade implica a falsidade.

OBS 1:
A condicional ou implicação é a operação lógica menos intuitiva
Declaração X: Se chover, então levo guarda-chuva
1 – Chove (V) e levo guarda-chuva (V)
2 – Chove (V) e não levo guarda-chuva (F)
3 – Não chove (F) e levo guarda-chuva (V)
4 – Não chove (F) e não levo guarda-chuva (F)
Em que situações é a declaração X verdadeira ou falsa?
Nas situações 1 (VV) e 4 (FF) é obviamente verdadeira.
Na situação 2 (VF) é obviamente falsa.
Na situação 3 (FV), menos obviamente, também é verdadeira
(não foi dito o que se faria caso não chovesse,
não foi dito que se levaria guarda-chuva se, e só se, chovesse)

OBS 2:
Se o cidadão é português, então é europeu.
VV
FV
Ser português Ser europeu
FF
Onde se representa a hipótese VF no gráfico ?

OBS 3:
1 – não importa o valor de verdade
de cada uma das proposições envolvidas (antecedente e consequente)
2 – não importa se há realmente conexão entre as proposições
3 – importa unicamente a relação entre os valores de verdade das proposições
Exemplos de condicionais verdadeiras:
“Se a Espanha é uma república, então fica na américa do sul” (FF)
“Se a Espanha é uma república, então fica na europa” (FV)
“Se a Espanha é uma monarquia, então fica na europa” (VV)
Exemplo de condicional falsa
“Se a Espanha é uma monarquia, então fica na américa do sul” (VF)

OBS 4:
A condicional ou implicação é o único operador binário que não é comutativo
(não é indiferente a ordem das proposições antecedente e consequente)
P Q P  Q Q  P
V V V V
V F F V
F V V F
F F V V
Quando o V implica o F a forma proposicional é F
mas
Quando o F implica o V a forma proposicional é V

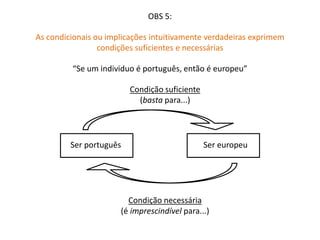
OBS 5:
As condicionais ou implicações intuitivamente verdadeiras exprimem
condições suficientes e necessárias
“Se um individuo é português, então é europeu”
Condição suficiente
(basta para...)
Ser português Ser europeu
Condição necessária
(é imprescindível para...)

OBS 6:
Variantes:
“Se um individuo é português, então é europeu”
A
Ideia sempre presente: o antecedente é condição suficiente do consequente
Se / caso / no caso de / sempre que o individuo é português, [então] é europeu
B
Ideia sempre presente: o consequente é condição necessária do antecedente
O cidadão [não] é português somente se / [...] a menos que / [...] a não ser que
for [seja] europeu

Bicondicional ou Equivalência – operação lógica e designação da proposição composta
Proposições
intervenientes
Linguagem natural
(frases + operador)
Formalização
Equivalentes
Um número é par se, e só
se, for divisível por dois.
Um número ser par
equivale a ser divisível
por dois.
PQ
P Q P  Q
V V V
V F F
F V F
F F V
Regra:
A bicondicional ou equivalência é verdadeira (falsa)
se as equivalentes tiverem valores de verdade iguais (diferentes).

OBS:
Cada uma das proposições equivalentes exprime
a condição suficiente e necessária do que é expresso pela outra
e,
por essa razão, as definições explícitas formulam-se através de equivalências
Variantes:
Um número é primo se, e só se / somente se / apenas se, é apenas divisível por si e
pela unidade
Dizer que uma figura geométrica é um triângulo equivale a dizer que tem três ângulos
Homem é animal racional
Se um número é par é divisível por dois e vice-versa

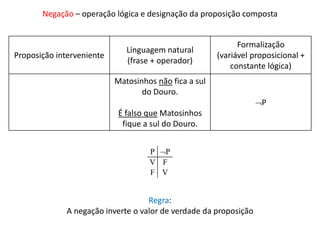
Negação – operação lógica e designação da proposição composta
Proposição interveniente
Linguagem natural
(frase + operador)
Formalização
(variável proposicional +
constante lógica)
Matosinhos não fica a sul
do Douro.
É falso que Matosinhos
fique a sul do Douro.
P
P P
V F
F V
Regra:
A negação inverte o valor de verdade da proposição

OBS:
A negação pode estar implícita: in(m)- / des- / a- / ...
nem (= e não)
Variantes
A situação é indesejável / desagradável /anormal / ...
Não é verdade que / não é o caso que / Matosinhos seja uma cidade do interior
O oceano que banha Matosinhos não é o Índico nem o Pacífico

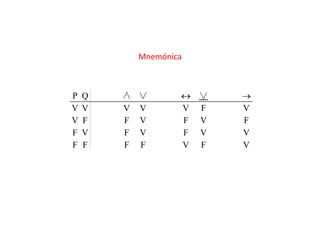
Mnemónica
P Q ∧ ∨  ∨ 
V V V V V F V
V F F V F V F
F V F V F V V
F F F F V F V

Formalização
1.º
Colocar a frase na forma canónica
2.º
Fazer a interpretação ou o dicionário
(sempre pela afirmativa)
3.º
Formalizar
(substituir cada frase por uma variável proposicional
e cada operador por uma constante lógica)

Âmbito dos operadores
Âmbito do operador = proposição(ões) afetada(s) pelo operador;
pode ser maior ou menor
Ao fazer as colunas da tabela de verdade segue-se por ordem crescente
de âmbito do operador
(começa-se pela do operador de menor âmbito
e acaba-se com a do operador de maior âmbito: operador principal)
1.º (das negações)  [ (P ∧ Q) ∨ R]  S
2.º (da conjunção)
3.º (da negação da conjunção)
4.º (da disjunção)
5.º (da negação da disjunção)
6.º (da condicional)

Erros na determinação do âmbito (frequentemente do âmbito da negação)
resultam em proposições não equivalentes
Dicionário: P = O aluno chega atrasado. Q = O aluno tem falta
 (P  Q)
1.ª
2.ª
P  Q)
1.ª
2.ª
É falso que se o aluno chega atrasado,
tem falta
Se o aluno não chega atrasado,
tem falta
P Q  (P  Q)
V V F V
V F V F
F V F V
F F F V
2.ª 1.ª
P Q P  Q
V V F V
V F F V
F V V V
F F V F
1.ª 2.ª
Nota: dizer “É falso que...” (no início da frase) em vez de “Não” reduz a ambiguidade.

Ambiguidade de âmbito
Ambiguidade de âmbito = situação em que há mais do que uma maneira
de entender o âmbito de um operador
Domingo vou à praia ou leio um livro e vou ao cinema
As vírgulas (na linguagem natural) tal como os parêntesis (na linguagem da lógica)
eliminam a ambiguidade
Domingo vou à praia,
ou leio um livro e vou ao cinema
Domingo vou à praia ou leio um livro,
e vou ao cinema

Domingo vou à praia,
ou leio um livro e vou ao cinema
Domingo vou à praia ou leio um livro,
e vou ao cinema
Interpretação: P = Domingo vou à praia. Q = Domingo leio um livro.
R = Domingo vou ao cinema
P Q R P ∨ (Q ∧ R)
V V V V V
V V F V F
V F V V F
V F F V F
F V V V V
F V F F F
F F V F F
F F F F F
2.ª 1.ª
P Q R (P ∨ Q) ∧ R
V V V V V
V V F V F
V F V V V
V F F V F
F V V V V
F V F V F
F F V F F
F F F F F
1.ª 2.ª
Conclusão: as duas proposições não são equivalentes

Unidade 3 cap 1.2 (a)

Mais conteúdo relacionado

Mais procurados

Semelhante a Unidade 3 cap 1.2 (a)

Unidade 3 cap 1.2 (a)