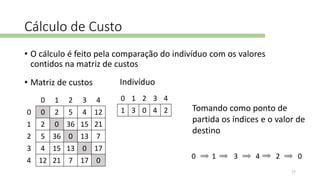
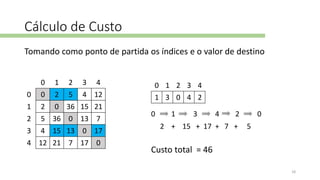
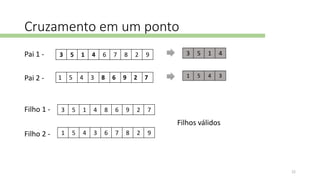
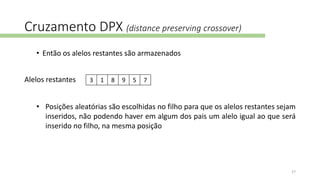
O documento descreve o problema do caixeiro-viajante, um problema NP-completo que envolve encontrar o caminho mais curto para visitar todos os nós de um grafo. Ele também discute abordagens para resolvê-lo, incluindo algoritmos genéticos e metaheurísticas, e apresenta a biblioteca TSPLIB, que fornece conjuntos de dados para teste.

1. Problema do caixeiro-viajante
(Traveling Salesman Problem)
1

2. O Problema do caixeiro-viajante
• O problema do caixeiro-viajante
• Dado um grafo G(N) e N o número de nós deste grafo, o problema
consiste em percorrer o menor ciclo do grafo (Ghoseiri e Sarhadi, 2007)
• Sendo Cij o valor a percorrer entre dois nós, o custo é o somatório dos
valores entre os nós percorridos (Ghoseiri e Sarhadi, 2007)
Resumindo
• Visitar todos os nós, passando por cada um uma única vez e retornando ao nó
de origem
2

3. O Problema do caixeiro-viajante
• A quantidade de possibilidades consiste na permutação da
quantidade de nós presentes no problema
• Para n nós há (n-1)! caminhos possíveis
• Um problema NP-Completo
• Problema de fácil compreensão e de difícil solução
3

4. O Problema do caixeiro-viajante
• Abordagem ótima
• Cálculo de custos de todos os trajetos possíveis e comparações entre eles
• Abordagens heurísticas e meta-heurísticas
• Abordagens que tentam encontrar uma boa solução para o problema
• Algoritmos genéticos
• Algoritmos meméticos
• Entre outras estratégias
4

5. Roteiro
• TSPLIB, formatos e leitura dos arquivos
• Gerar novos indivíduos
• Criar população inicial
• Escolha de indivíduo
• Operadores de cruzamento
• Cruzamento em um ponto
• Uniforme
• Distance Preserving Crossover
• Cycle Crossover
• Cálculo de custo total
5

6. Biblioteca TSPLIB
• Biblioteca criada em 1990 por Reinelt
• Contém mais de 100 exemplos, variando de 14 a 85.900 cidades
(Álvaro, 2006)
• Informações dos arquivos
• Nome: identificação do arquivo
• Tipo: PCV
• Comentário: nome do criador ou contribuinte do problema
• Dimensão: número de nós do problema
6

7. Biblioteca TSPLIB
• Tipo do peso da aresta: explicita o cálculo que deve ser feito para se ter a
distância entre dois nós
• explícito: não será necessário cálculo
• distância euclidiana, máxima ou manhatan (quarteirão)
• distância geográfica
• Formato das arestas: informa como estão dispostos os nós no arquivo, como
eles devem ser lidos para criação da matriz de custos
• Matriz completa
• Matriz triangular superior ou inferior
• Com diagonal ou sem diagonal
7

8. Biblioteca TSPLIB
• Exemplo de arquivos da biblioteca TSPLIB
Exemplo 2 – Coordenadas geográficasExemplo 1 – Coordenadas explicita
8

9. Biblioteca TSPLIB
• Com a leitura seguindo os critérios definidos pelo arquivo é montada
a matriz de custos
• Quando um cálculo é necessário para determinar o valor dos custos, o valor é
aproximado segundo notação científica
9

10. Biblioteca TSPLIB – Matriz de custos
• Com a devida leitura do arquivo, uma matriz de custos é gerada
• Exemplo da matriz de custos
Alguns arquivos – que trazem os pesos
diagonais da matriz – utilizam do valor 0
ou 9999 para simular a impossibilidade
de ir de uma localidade a outra
0 1 2 3
0 0 2 5 4
1 2 0 36 15
2 5 36 0 13
3 4 15 13 0
10

11. Gerar Novos Indivíduos
• Os novos indivíduos são representados por vetores, sendo que nestes
são inseridos os valores que vão de 0 à dimensão do problema menos
um
• Um valor não pode ser inserido no índice que lhe corresponde
• Ex.: O valor 0 não pode ser inserido na primeira posição do vetor
11

12. Gerar Novos Indivíduos
• Para um problema de dimensão 4
0 1 2 3 4 5 6 7
0 7 5 4 6 1 3 2
Índice
Isso implica ir do nó 0 para o nó 0, o que não condiz com o PCV
Também não são criadas conexões entre nós que pela matriz de custos não estão
conectados
12

13. Gerar Novos Indivíduos
• Um novo indivíduo é gerado aleatoriamente, seguindo os seguintes
passos:
• Valores são escolhidos aleatoriamente
• Os rótulos dos nós são inseridos nas posições correspondentes aos valores
gerados anteriormente, seguindo as restrições anteriores
13

14. Gerar Novos Indivíduos
• Escolhendo aleatoriamente as posições 4, 0 e 7, inserimos os valores
0, 1 e 2 nestas posições, respectivamente
0 1 2 3 4 5 6 7
1 0 2
• Escolhemos a posição 3 para a inserção do valor 3...
0 1 2 3 4 5 6 7
1 3 0 2
... o que não pode ocorre. Então devemos escolher outra posição para
alocar o valor 3 e continuar o processo
14

15. Gerar novos indivíduos
• Alguns arquivos da TSPLIB trazem arestas (conexões) entre nós pré-
estabelecidas
• Assim, sempre que um arquivo trouxer a seção
FIXED_EDGES_SECTION (seção de arestas fixas), alguns nós serão
inseridos no indivíduo de forma premeditada
15

16. Escolha de Indivíduos
• Um indivíduo é escolhido aleatoriamente na população
• O mesmo indivíduo não pode ser escolhido para o mesmo processo
16

17. Cálculo de Custo
• O cálculo é feito pela comparação do indivíduo com os valores
contidos na matriz de custos
• Matriz de custos
0 1 2 3 4
0 0 2 5 4 12
1 2 0 36 15 21
2 5 36 0 13 7
3 4 15 13 0 17
4 12 21 7 17 0
0 1 2 3 4
1 3 0 4 2
Indivíduo
Tomando como ponto de
partida os índices e o valor de
destino
0 1 3 4 2 0
17

18. Cálculo de Custo
Tomando como ponto de partida os índices e o valor de destino
0 1 3 4 2 0
0 1 2 3 4
1 3 0 4 2
0 1 2 3 4
0 0 2 5 4 12
1 2 0 36 15 21
2 5 36 0 13 7
3 4 15 13 0 17
4 12 21 7 17 0
2 + 15 + 17 + 7 + 5
Custo total = 46
18

19. • Neste operador cada pai é dividido em um ponto escolhido
aleatoriamente, e separado em duas partes, e então suas partes são
comutadas, gerando assim dois novos indivíduos
• Exemplo de cruzamento em um ponto para indivíduos binários
Pai 1 -
Pai 2 -
Cruzamento em um ponto
1 0 0 1 1 0 0 0
0 1 1 1 0 1 0 0 0 1 1 1 0 0 0 0
1 0 0 1 1 1 0 0
Filho 1 -
Filho 2 -
19

20. Cruzamento em um ponto
• Exemplo de cruzamento de um indivíduo decimal:
1 5 4 6 8 3 9 2 7
3 5 1 4 6 7 8 2 9 3 5 1 4 8 3 9 2 7
1 5 4 6 6 7 8 2 9
Filho 1 -
Filho 2 -
Pai 1 -
Pai 2 -
3 5 1 4 8 3 9 2 7
1 5 4 6 6 7 8 2 9
Os indivíduos não são válidos
Filho 1 -
Filho 2 -
20

21. Cruzamento em um ponto
• Verificar se os possíveis filhos serão validos após o cruzamento
• Escolhemos a parte que contém o menor lado a partir do ponto de divisão e é
feita a comparação entre as partes de ambos os pais
1 5 4 6 8 3 9 2 7
3 5 1 4 6 7 8 2 9Pai 1 -
Pai 2 - 1 5 4 6
3 5 1 4
Neste exemplo, os filhos não manterão a consistência
21

22. Cruzamento em um ponto
1 5 4 3 8 6 9 2 7
3 5 1 4 6 7 8 2 9
3 5 1 4 8 6 9 2 7
1 5 4 3 6 7 8 2 9
Filho 1 -
Filho 2 -
Pai 1 -
Pai 2 - 1 5 4 3
3 5 1 4
Filhos válidos
22

23. Cruzamento Uniforme
• Aleatoriamente um pai é escolhido para que um alelo seja herdado
• Se tal alelo já tiver sido herdado, parte-se para o outro pai
• Exemplo de cruzamento uniforme
1 5 4 6 8 3 9 2 7
3 5 1 4 6 7 8 2 9Pai 1 -
Pai 2 -
Escolhemos primeiro o Pai 2
1Filho -
23

24. Cruzamento uniforme
1 5 4 6 8 3 9 2 7
3 5 1 4 6 7 8 2 9Pai 1 -
Pai 2 -
Em seguida os pais 2 e 1, respectivamente
1 5 1Filho -
Houve uma perda na factibilidade do filho, e assim é escolhido o alelo que está
contido no outro pai, Pai 2
1 5 4Filho -
24

25. Cruzamento uniforme
Repete-se o procedimento até se completar o filho
1 5 4 6 8 3 9 2 7Filho -
1 5 4 6 8 3 9 2 7
3 5 1 4 6 7 8 2 9Pai 1 -
Pai 2 -
Se não for possível a escolha de um alelo de um dos pais, o cruzamento é abortado
25

26. Cruzamento DPX (distance preserving crossover)
• Baseia-se na distância entre os pais, ou seja, no número de alelos
diferentes entre os pais (D’Martin, 2002)
• Supondo dois pais tomados aleatoriamente, todos os alelos comuns aos dois
pais são copiados para o filho
5 7 6 3 2 4 8 9 1
3 1 6 8 2 4 9 5 7Pai 1 -
Pai 2 -
6 2 4Filho -
26

27. Cruzamento DPX (distance preserving crossover)
• Então os alelos restantes são armazenados
3 1 8 9 5 7Alelos restantes
• Posições aleatórias são escolhidas no filho para que os alelos restantes sejam
inseridos, não podendo haver em algum dos pais um alelo igual ao que será
inserido no filho, na mesma posição
27

28. Cruzamento DPX (distance preserving crossover)
3 1 8 9 5 7Alelos restantes
3 6 2 4Filho -
3 6 2 4 1Filho -
8 3 6 2 4 1Filho -
8 3 6 9 2 4 7 1 5Filho -
Filho resultante
28

29. Cruzamento CX (Cycle Crossover)
• Primeiramente todos os alelos comuns a ambos os pais são copiados
para o filho
6 7 5 3 2 4 8 9 1
3 1 5 8 2 4 9 6 7Pai 1 -
Pai 2 -
5 2 4Filho -
29

30. Cruzamento CX (Cycle Crossover)
• Um ponto – o qual no filho encontra-se vazio – e um pai são
escolhidos aleatoriamente no início
6 7 5 3 2 4 8 9 1Pai 2 -
O alelo selecionado é inserido no filho na posição que corresponde ao pai
sorteado
5 3 2 4Filho -
30

31. Cruzamento CX(Cycle Crossover)
• Então, o valor não selecionado (no outro pai) é inserido no filho, na
posição que se encontra no pai sorteado anteriormente
6 7 5 3 2 4 8 9 1
3 1 5 8 2 4 9 6 7Pai 1 -
Pai 2 -
5 3 2 4 8 9Filho -
31

32. Cruzamento CX (Cycle Crossover)
• O procedimento é repetido até que alguma posição já esteja ocupada
5 3 2 4 8Filho -
5 3 2 4 8 9Filho -
6 5 3 2 4 8 9Filho -
6 7 5 3 2 4 8 9 1
3 1 5 8 2 4 9 6 7Pai 1 -
Pai 2 -
32

33. Cruzamento CX (Cycle Crossover)
• Então se busca pela posição vazia mais à esquerda, e é feita a troca
dos pais, atribuindo a esta posição o valor encontrado no pai atual
6 5 3 2 4 8 9 7Filho -
6 7 5 3 2 4 8 9 1
3 1 5 8 2 4 9 6 7Pai 1 -
Pai 2 -
33

34. • Filho resultante
Cruzamento CX(Cycle Crossover)
6 1 5 3 2 4 8 9 7Filho -
6 7 5 3 2 4 8 9 1
3 1 5 8 2 4 9 6 7Pai 1 -
Pai 2 -
• O processo continua até que todo o filho tenha sido preenchido,
inclusive com outras trocas entre os pais, se necessário
34

35. Referências
• Thiago D’Martin Maia – 2002 – Uma Avaliação de Meta-heurísticas
para o Problema de Designação Quadrática
• Álvaro Nunes Prestes – 2006 – Uma Análise Experimental de
Abordagens Heurísticas ao Problema do caixeiro-viajante.
• Keivan Ghoseiri, Hassan Sarhadi – 2007 – A memetic algorithm for
symmetric traveling salesman problem
• http://www.me.utexas.edu/~jensen/ORMM/models/unit/combinator
ics/tsp.html
35