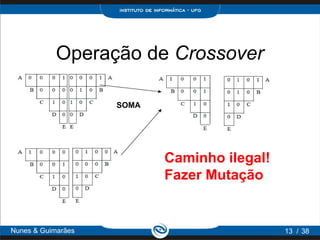
O documento apresenta uma introdução aos algoritmos genéticos e descreve dois problemas que serão resolvidos: o problema do caixeiro viajante e o tratamento quimioterápico, incluindo suas representações e soluções propostas utilizando técnicas de algoritmos genéticos como seleção, crossover e mutação.

1. Algoritmos Genéticos
Prática
Profª. Rosângela Nunes
Prof. Norton Guimarães
Nunes & Guimarães 1 / 38

2. Agenda
Introdução
Problema 01
Problema 02
Nunes & Guimarães 2 / 38

3. Introdução
Nunes & Guimarães 3 / 38

4. Introdução
●
O Algoritmo Genético foi desenvolvido por
John Holland, nos meados dos anos de
1960 e 1970, com base na teoria da
Evolução de Charles Darwin e
popularizado por David Goldberg, através
da resolução de um problema,
envolvendo o controle de transmissão de
gasoduto.
Nunes & Guimarães 4 / 38

5. O que são Algorítmos
Genéticos?
“Uma técnica de busca baseada numa
metáfora do processo biológico de evolução
natural” [LINDER, 2012].
Nunes & Guimarães 5 / 38

6. Os Problemas
●
Uma nova abordagem do problema
clássico caixeiro viajante
●
Tratamento Quimioterápico
Nunes & Guimarães 6 / 38

7. O problema do caixeiro viajante
O problema consistem em um caixeiro
viajante, partindo de sua cidade, deve visitar
exatamente uma única vez cada cidade de
uma dada lista e retornar para casa tal que a
distância total percorrida seja a menor
possível.
Nunes & Guimarães 7 / 38

8. A Representação Binária
O encontro de uma
cidade com outra
será representado
pelo bit 1 e a não
ligação pelo bit 0.
Nunes & Guimarães 8 / 38

9. A nova proposta
A leitura na matriz é
dada da esquerda
para direita e de
cima para baixo no
primeiro triângulo
e da esquerda
para direita e de
baixo para cima no
segundo triângulo.
Nunes & Guimarães 9 / 38

10. A validação
Para ser válida a matriz deve atender:
1 - O número de elementos (1) deve ser
igual ao número de cidades nos dois
lados;
2 – Só pode ter um elemento (1) por linha e
coluna;
3 – No mesmo vértice a soma de elementos
Nunes (1) deve ser igual a 2.
& Guimarães 10 / 38

11. A Seleção dos Pais
A seleção dos pais é de acordo com o seu
ranking e escolhe sempre os menores.
Nunes & Guimarães 11 / 38

12. A Seleção dos Pais
De acordo com a
seleção devemos
escolher os
valores
(17,22,23,24)
Nunes & Guimarães 12 / 38

13. Operação de Crossover
SOMA
Caminho ilegal!
Fazer Mutação
Nunes & Guimarães 13 / 38

14. Operação de Mutação
Conta o número de elemento
com (1) o valor em cada linha
e coluna para a cidade, se o
número for superior a 2, em
seguida, repetir excluindo a
extremidade mais comprida
do passeio resultante até que
o número de elementos no
caminho resultante é igual a 2.
No entanto, se o número de
elementos no caminho
resultante é inferior a 2
adicionaremos as arestas que
faltam no caminho pelo
algoritmo guloso.
Nunes & Guimarães 14 / 38

15. O resultado
Nunes & Guimarães 15 / 38

16. O problema de Tratamento
Quimioterápico
A escolha do melhor tratamento pelos
médicos é uma tarefa complexa e, muitas
vezes, pode determinar a vida de uma
pessoa.
O tratamento quimioterápico do câncer
pode ser paliativo ou curativo.
Nunes & Guimarães 16 / 38

17. A Representação
O vetor de decisão , onde (Ci j)
representa o nível de concentração das drogas, n os ciclos
do tratamento e das drogas que compõem o coquetel anti-
cancer.
O vetor de decisão acima foi codificado por uma string binária
em que cada concentração e Ci j é expressada por um
conjunto de 4(quatro) alelos binários. Desta forma o
cromossoma foi definido como
Nunes & Guimarães 17 / 38

18. A Representação
Uma segunda forma de representação denominada cycle-wis e
variable representation.
Nunes & Guimarães 18 / 38

19. Solução 1
Seleção dos pais: Método de roleta viciada.
CrossOver de dois pontos
Mutação bit-wise
Nunes & Guimarães 19 / 38

20. Solução 2
Adaptive Elitiist-Population based Genetic Algorithm – AEGA,
foi utilizado.
Ajuste do tamanho da população de forma adaptativa
com o objetivo de buscar pelo menos um indivíduo em
cada pico e realizar esta busca em paralelo para todos
os picos.
Operadores genéticos:
Operador de crossover elitista
Operador de mutação elitista.
Nunes & Guimarães 20 / 38

21. Direção relativa entre dois
cromossomos
Nunes & Guimarães 21 / 38

22. A Operação Crossover
Se pais e filhos estiver na
mesma base de
atração
Eliminar o menos apto
Escolher os dois mais
aptos
Nunes & Guimarães 22 / 38

23. A Operação Elistista de
Mutação
Escolha randômica
Indivíduo, Posição do cromossomo e Valor
Se filho estiver numa área do espaço de
solução não explorado
Mantém pai e filho na próxima geração
Caso contrário
Mantém o mais apto
Nunes & Guimarães 23 / 38

24. Referências
[1] DARWIN, C. A Origem das Espécies. LELLO & IRMÃO-
EDITORES, 1859.
[2] HAUPT, R.; HAUPT, S. E. Practical Genetic Algorithms. Wiley, 2th
edition, 2004.
[3] KHAN, H. F. e. a. Solving tsp problem by using generic algorithm.
International Journal of Basic & Applied Sciences, 9(10):79–88, 12
2009.
[4] Liang, Y.; Lueng, K.; Mok, T. S. K. Automating the drug scheduling
with differente toxicity clearance in cancer chemotherapy via
evolutionary computation. Genetic and Evolutionary Computation
Conference, 2006.
Nunes & Guimarães 24 / 38

25. Referências
[5] LINDER, R. Algoritmos Genéticos. Brasport, 2th edition, 2008.
[6] PACHECO, Marco Aurélio e FUKASAWA, R. resolução do
problema do entregador viajante. In: Revista de Inteligência
Computacional Aplicada - PUC Rio, 2010.
[7] Petrovski, A.; MacCall, J. Smart problema solving environmnt for
medical decision support. Genetic and Evolutionary Computation
Conference, 2005.
Nunes & Guimarães 25 / 38