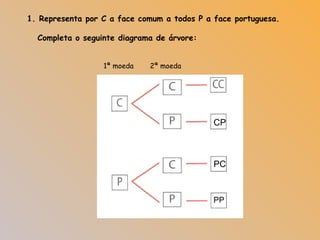
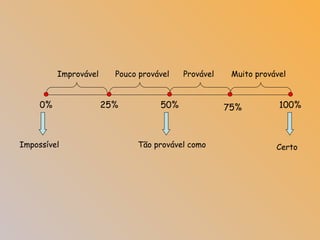
1) O documento discute a lei de Laplace e probabilidades de eventos em jogos de azar e experiências aleatórias. 2) É apresentado um jogo com moedas onde os jogadores lançam duas moedas e tentam fazer combinações para pontuar. 3) Explica-se como calcular probabilidades usando a fórmula de Laplace, com exemplos como lançar dados e tirar frutas de um cesto.

1. Sumário
Probabilidade de um acontecimento
Lei de Laplace.

2. PROBABILIDADE DE UM ACONTECIMENTO
Lei de LAPLACE
1749 - 1827

3. Actividade 1
Jogo das Moedas
Número de jogadores:
Dois jogadores ou duas equipas
Material:
2 moedas de um euro; papel e lápis
Regras do jogo:
Um dos jogadores será o A e o outro será o B.
Cada jogador, na sua vez, atira duas moedas ao ar. Se sair
as duas faces comuns a todos os países da União Europeia, o
B ganha um ponto; caso contrário, ganha o A um ponto.
O vencedor é aquele que obtiver maior pontuação ao fim
de dez lançamentos.

4. 1. Representa por C a face comum a todos P a face portuguesa.
Completa o seguinte diagrama de árvore:
1ª moeda 2ª moeda
CP
PC
PP

5. 2. Os dois jogadores têm as mesmas hipóteses de ganhar? Porquê?
Não, porque as duas faces C saem uma vez, as outras saem três vezes
3. Se fosses tu a jogar, quem escolherias ser? 0 A ou o B?
CP PC PPCC
Escolhia o A.

6. Lei de LAPLACE
EXPERIÊNCIA: Lançamento de uma moeda
E = { N, C }
A moeda tem duas faces: N – nacional; C - Comum
Qual é a probabilidade de sair N no lançamento de uma moeda?
( )P N =
Número de casos favoráveis
Número de casos possíveis
Nº casos favoráveis = 1
Nº casos possíveis = 2
( )
1
P F = = 0,5 =50%
2

7. EXPERIÊNCIA: Lançamento de um dado equilibrado
( )
nº de casos favoráveis 1
P A = =
nº de casos possíveis 6
Calcula a probabilidade de cada um dos acontecimentos:
A: “ Sair o número 5 “1) Só há uma
face “5”
Um dado
tem 6
faces
2) B: “ Sair um número maior que 2 “
Nº casos favoráveis = 4
Nº casos possíveis = 6
( )
3
2
6
4
==BP
B = { 3, 4, 5, 6 }

8. Num cesto de fruta há: 10 laranjas, 8 maçãs e 2 peras.
Tira-se ao acaso uma peça de fruta do cesto. Qual a
probabilidade de ser:
uma maçã
nº de casos favoráveis:
nº de casos possíveis:
P(sair maçã)
uma pêra
nº de casos favoráveis:
nº de casos possíveis:
P(sair pêra)
8
10+8+2=20
8
20
=
2
5
= 0,4= 40%=
2
10+8+2=20
2
20
=
1
10
= 0,1= 10%=

9. uma laranja
nº de casos favoráveis:
P(sair laranja)
uma maçã ou uma pêra
nº de casos favoráveis:
P(sair pêra)
10
10
20
=
1
2
= 0,5= 50%=
Um limão
nº de casos favoráveis:
P(sair limão)
uma maçã ou uma pêra ou uma
laranja
nº de casos possíveis:
P(sair ……)
0
0
20
= 0= 0%=
20
20
20
= 1= 100%=
10
10
20
=
1
2
= 0,5= 50%=
Acontecimento
impossível
A probabilidade de sair um
acontecimento impossível é 0
Acontecimento certo
A probabilidade de sair um
acontecimento certo é 1

10. De um modo geral
0 ( ) 1P A≤ ≤
0% ( ) 100%≤ ≤P A

11. 0% 25% 50% 75% 100%
Impossível
Improvável Pouco provável
Tão provável como
Provável Muito provável
Certo