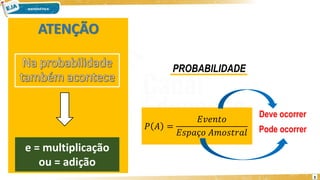
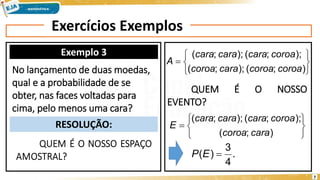
O documento apresenta exercícios e resoluções sobre probabilidade, abordando eventos e espaços amostrais em lançamentos de moedas e dados. Exemplos incluem determinar a probabilidade de obter eventos específicos, como a face cara de uma moeda ou a soma de pontos em dados. O conteúdo visa ilustrar conceitos fundamentais de probabilidade por meio de exercícios práticos.

2. 2

3. 𝑃 𝐴 =
𝐸𝑣𝑒𝑛𝑡𝑜
𝐸𝑠𝑝𝑎ç𝑜 𝐴𝑚𝑜𝑠𝑡𝑟𝑎𝑙
e = multiplicação
ou = adição
PROBABILIDADE
Deve ocorrer
Pode ocorrer
ATENÇÃO
3

4. 4

5. Exercícios Exemplos
Exemplo 1 RESOLUÇÃO:
No lançamento de uma moeda,
qual é a probabilidade de se
obter a face cara?
QUEM É O NOSSO ESPAÇO
AMOSTRAL?
 
coroa
cara
A ;

QUEM É O NOSSO
EVENTO?
 
cara
E  .
2
1
)
( 
E
P
5

6. Exercícios Exemplos
Exemplo 2 RESOLUÇÃO:
No lançamento de um dado, qual
é a probabilidade de se obter na
face voltada para cima, um
número de pontos menor que
três?
QUEM É O NOSSO ESPAÇO
AMOSTRAL?
QUEM É O NOSSO
EVENTO?
 
2
;
1

E .
3
1
6
2
)
( 

E
P
 
6
;
5
;
4
;
3
;
2
;
1

A
6

7. Exercícios Exemplos
Exemplo 3
RESOLUÇÃO:
No lançamento de duas moedas,
qual e a probabilidade de se
obter, nas faces voltadas para
cima, pelo menos uma cara?







)
;
(
);
;
(
);
;
(
);
;
(
coroa
coroa
cara
coroa
coroa
cara
cara
cara
A
QUEM É O NOSSO
EVENTO?







)
;
(
);
;
(
);
;
(
cara
coroa
coroa
cara
cara
cara
E
.
4
3
)
( 
E
P
7

8. Exercícios Exemplos
Exemplo 4
RESOLUÇÃO:
No lançamento de dois dados, qual
e a probabilidade de se obter, nas
faces voltadas para cima, a soma
dos pontos igual a 5?
QUEM É O NOSSO
EVENTO?
 
)
1
;
4
(
),
2
;
3
(
),
3
;
2
(
),
4
;
1
(

E
.
9
1
36
4
)
( 

E
P
36
)
( 
A
n
AMOSTRAL
ESPAÇO
NOSSO
O
TEM
ELEMENTOS
QUANTOS
8

9. Exercícios Exemplos
Exemplo 5
RESOLUÇÃO:
No lançamento de um dado, qual é
a probabilidade de se obter, na
face voltada para cima, um
número par de pontos?
QUEM É O NOSSO
EVENTO?
 
6
;
4
;
2

E
.
2
1
6
3
)
( 

E
P
 
6
;
5
;
4
;
3
;
2
;
1

A
9

10. Exercícios Exemplos
Exemplo 6
RESOLUÇÃO:
No lançamento de dois dados, qual
e a probabilidade de se obter, nas
faces voltadas para cima, a soma
dos pontos igual a 7?
QUEM É O NOSSO
EVENTO?







)
1
;
6
(
),
2
;
5
(
),
3
;
4
(
),
4
;
3
(
),
5
;
2
(
),
6
;
1
(
E
.
6
1
36
6
)
( 

E
P
36
)
( 
A
n
AMOSTRAL
ESPAÇO
NOSSO
O
TEM
ELEMENTOS
QUANTOS
10

11. Exercícios Exemplos
Exemplo 7
RESOLUÇÃO:
Uma urna contém exatamente
cem etiquetas numeradas de 1 a
100. Retirando uma etiqueta dessa
urna, qual é a probabilidade de
obtermos um número menor do
que 41?
.
5
2
100
40
)
( 

E
P
.
100
)
( 
A
n
AMOSTRAL
ESPAÇO
NOSSO
O
TEM
ELEMENTOS
QUANTOS
.
40
)
( 
E
n
EVENTO
NOSSO
O
TEM
ELEMENTOS
QUANTOS
11

12. Exercícios Exemplos
Exemplo 8
Em uma indústria com 4000
operários, 2100 têm mais de 20
anos, 1200 são especializados e 800
têm mais de 20 anos e são
especializados. Se um dos operários
é escolhido aleatoriamente, a
probabilidade de ele ter no máximo
20 anos e ser especializado é:
18
7
E)
85
27
D)
8
3
C)
5
2
B)
10
1
A)
12

13. Exercícios Exemplos
Exemplo 8
18
7
E)
85
27
D)
8
3
C)
5
2
B)
10
1
A)
Total de operários = 4000
2100 tem mais de 20 anos.
1200 são especializados.
800 tem mais de 20 anos e são
especializados.
1200 - 800 = 400.
400 são especializados e menor
ou igual a 20 anos
𝑃 𝐸 =
400
4000
𝑃 𝐸 =
4
40
𝑃 𝐸 =
1
10
13

14. Exercícios Exemplos
Exemplo 9
(Enem 2015) Em uma central de
atendimento, cem pessoas
receberam senhas numeradas de
1 até 100 Uma das senhas é
sorteada ao acaso.
Qual é a probabilidade de a senha
sorteada ser um número de 1 a
20?
100
80
E)
100
21
D)
100
20
C)
100
19
B)
100
1
A)
𝟏𝟎𝟎
𝑃 𝐸 =
20
100
𝑃 𝐸 =
2
10
𝑃 𝐸 =
1
5
14