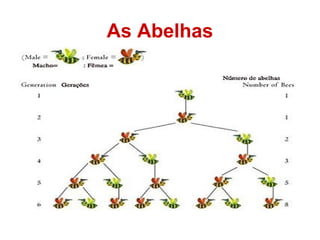
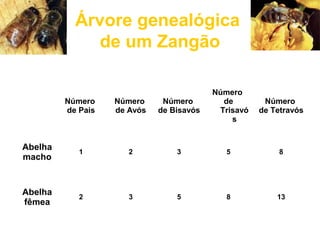
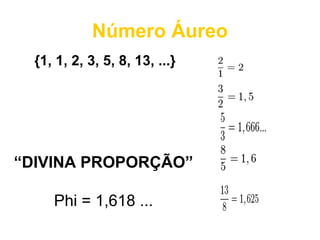
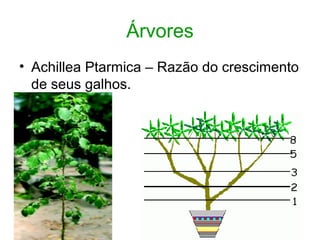
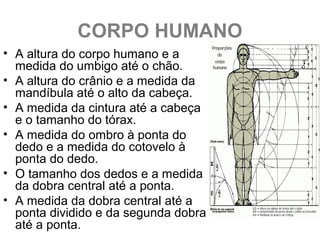
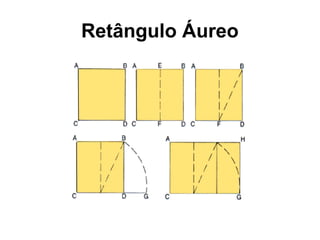
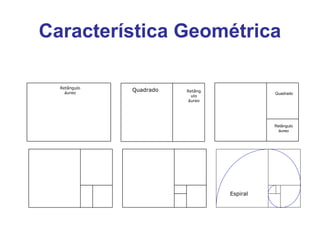
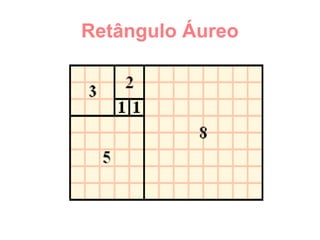
O documento discute a sequência de Fibonacci e como o número áureo, também conhecido como número de ouro, aparece na natureza, arte, arquitetura e outras áreas. A sequência de Fibonacci é exemplificada e como ela se relaciona com a proporção áurea é explicado. Exemplos de como a proporção áurea aparece em plantas, frutas, animais e no corpo humano são fornecidos.