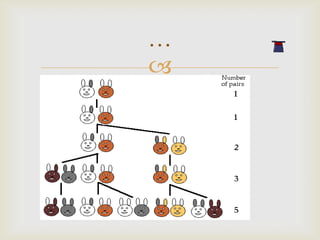
O documento discute a vida e obra de Fibonacci, introduzindo a sequência de Fibonacci e sua relação com o número de ouro. A sequência de Fibonacci aparece na natureza, incluindo o crescimento de plantas, a forma de moluscos e a reprodução de coelhos. O documento também explora como a proporção áurea influenciou a arte e música.

2. ÍNDICE

 Vida de Fibonacci…
 Origem da sequencia de Fibonacci…
 O número de ouro…
 Relação entre a sequencia de Fibonacci e o número de ouro…
 Fibonaccina: Arte, Música,Plantas, Moluscos,Coelhos…
 O que é realmente….
 Conclusão…
 Identificação…

3. A vida de Fibonacci

 Fibonacci nasceu por volta de 1180 em Pisa, uma das
primeiras cidades comerciais italianas e que manteve
um comércio florescente com o mundo árabe. O pai
de Fibonacci era um mercador que trabalhou no
norte de África, pelo que cedo Fibonacci foi iniciado
nos negócios e nos cálculos, o que despertou o seu
interesse pela matemática. Além disso, foi através da
profissão do pai que ele teve o primeiro contacto
com o sistema decimal hindu-árabe. Nesta altura, era
ainda utilizada a numeração romana em Itália.

4. A origem da sêquencia

 No livro a que nos referimos anteriormente, Líber
Abaci, Fibonacci introduziu um problema por ele
formulado que veio dar origem posteriormente a
uma sucessão. Essa sucesão ficou conhecida na
história como a Sucessão de Fibonacci e teve lugar no
ano de 1202, quando Fibonacci se interessou pela
reprodução dos coelhos. Ele criou então um cenário
imaginário com as condições ideais, sob as quais os
coelhos se poderiam então procriar.

5. O número de ouro

 O Número de Ouro é um número irracional
misterioso e enigmático que nos surge numa
infinidade de elementos da natureza na forma de
uma razão, sendo considerada por muitos como uma
oferta de Deus ao mundo.

6. Relação entre o númro de ouro e
a sequencia de FIBONACCI

 O número de ouro tem o valor j = ( 1 + Ö 5 )/2 (= 1,618
033 989...) Na secção da Sucessão de Fibonacci, temos a
seguinte sequência de números 1, 1, 2, 3, 5, 8, 13, 21, 34,
55, 89, 144, 233....
Se dividirmos cada um destes números pelo seu
antecedente, reparamos que essa razão vai ir para um
certo valor.
Isto é, se fizermos F2/F1=1; F3/F2=2; F4/F3=1,5;
F5/F4=1,6(6); F6/F5=1,6 e se continuarmos assim
sucessivamente, obtemos a seguinte sequência de
números:

7. …

 1,000 000; 2,000 000; 1,500 000; 1,666 666; 1,600 000;
1.625 000; 1,615 385; 1,619 048; 1,617 647; 1,618 182;
1,617 978; 1,618 056; 1,618 026; 1,618 037; 1,618 033; ...
Então Fn+1/Fn aproxima-se cada vez mais de j(Phi)
Esta expansão decimal prolongar-se-á sem nunca se
repetir (logo é um número irracional).
De facto, quando se prolongam estas "razões de
Fibonacci" indefinidamente, o valor gerado,
aproxima-se cada vez mais do número de ouro.

8. Fibonacci na arte

 Muitos artistas que viveram depois de Phidias
usaram a proporção Áurea em seus trabalhos. Da
Vinci a chamava: Divina Proporção e a usou em
muitos de seus trabalhos. Na Mona Lisa observa-se a
proporção Áurea em várias situações. Por exemplo,
ao construir um retângulo em torno de seu rosto,
veremos que este possui a proporção do retângulo
Áureo.

9. …

 . Podemos também subdividir este retângulo usando
a linha dos olhos para traçar uma reta horizontal e
ter de novo a proporção Áurea. Podemos continuar a
explorar tal proporção em várias outras partes do
corpo. Artistas têm usado a razão de ouro (medida
de Ouro) em trabalhos de pintura e arte. Os
trabalhos de Seurat e Mondrian mostram estas
relações matemáticas.

10. Fibonacci na música

 O número de ouro está presente nas famosas
sinfonias Sinfonia n.º 5 e a Sinfonia n.º 9, de Ludwig
van Beethoven, e em outras diversas obras. Outro
fato interessante registrado na Revista Batera, em um
artigo sobre o baterista de jazz Max Roach, é que, em
seus solos curtos, aparece tal número, se
considerarmos as relações que aparecem entre
tempos de bumbo e caixa. O compositor húngaro
Béla Bartók utiliza esta relação de proporcionalidade
constantemente em sua obra. Este fato pode ser visto
na análise da música de Bartók feita por Ernö
Lendvai (Béla Bartók: And Analysis of his Music).

11. Fibonacci nas palntas

 Certas plantas mostram os números de Fibonacci no crescimento de
seus galhos. Suponhamos que nasça um novo broto de um galho a
cada mês, sendo que um broto leva dois meses para produzir o seu
primeiro broto.
 Existem várias plantas cujo crescimento se parecem com o descrito
aqui. A planta Achillea ptarmica possui estas características.

12. Fibonacci nos moluscos

 Os moluscos estão relacionados com espirais tais
como a couve flor.

13. Fibonacci nos coelhos

 Condições:
 No primeiro mês temos um coelho macho e um
coelho fêmea. Estes dois coelhos acabaram de nascer.
Um coelho só atinge a maturidade sexual ao fim de
um mês. O período de gestação de um coelho dura
um mês. Ao atingirem a maturidade sexual, a fêmea
irá dar à luz todos os meses. A mãe irá dar todos os
meses um coelho macho e um coelho fêmea. Os
coelhos nunca morrem.

14. …


15. MAS AFINAL QUAL É A
SEQUENCIA DE FIBONACCI?

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,…

16. CONCLUSÃO

 Com este trabalho aprendi que a sequencia de
Fibonacci aplica-se em varias coisas no nosso dia-a-
dia.
 Fiquei a saber quem é realmente Fibonacci e o que
fez de importante na matemática.

17. Identificação

Trabalho Realizado por: Ana Rita Flores
Afonso
nº3 7ºA