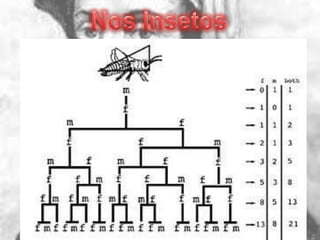
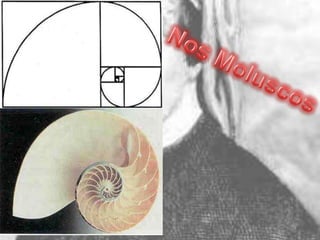
Este documento resume a vida e trabalho de Fibonacci, incluindo a origem da sequência de Fibonacci e sua relação com o número de ouro. Ele também fornece exemplos de como a sequência aparece na natureza e explica como os problemas de Fibonacci são resolvidos.

2.  Introdução;
 Um resumo da história da vida de Fibonacci;
 A origem da sequência de Fibonacci;
 O numero de ouro (ou a razão dourada);
 A relação entre a sequência de Fibonacci e
o numero de ouro;
 Exemplos da sequencia de Fibonacci na:
Arte, Musica, Plantas, Insetos, Moluscos,
Coelhos,…;
 A resolução dos desafios sobre Fibonacci.

3. Na disciplina de Matemática foi-nos proposto um
trabalho sobre Fibonacci .
Nele vamos falar sobre a vida de Fibonacci, a origem
da sequência de Fibonacci, o número de ouro, a
relação entre a sequência de Fibonacci e o
número de ouro, exemplos da sequência de
Fibonacci na: Arte, Musica, Plantas, Insetos,
Moluscos, Coelhos.
E vamos mostrar a resolução dos desafios sobre
Fibonacci.
Esperamos que o trabalho esteja explicito e claro
em toda e informação.

4. Leonardo de Pisa (1180-1250) mais
conhecido como Fibonacci foi um
Matemático Italiano. É considerado por
muitos como o mais talentoso matemático
ocidental da Idade Media.
Ficou conhecido pela descoberta da
Sequência de Fibonacci e pelo seu papel
na introdução dos algarismos arábicos na
Europa.

5. Na natureza, alguns fenômenos
parecem obedecer a um padrão
numérico - como é o caso da velocidade
com que os coelhos se reproduzem. O
mais intrigante é que esses números
guardam, entre si, uma proporção. Essa
sequência de números é chamada de
sequência de Fibonacci.

6. O número de ouro tem o valor Phi =
( 1 + √ 5 ):2 =( 1,618 033 989...)

7. Na sequencia de Fibonacci, temos a
seguinte sequência de números 1, 1, 2,
3, 5, 8, 13, 21, 34, 55, 89, 144, 233.... Se
dividirmos cada um destes números
pelo seu antecedente, reparamos que
essa razão vai ter um certo valor.

8. Isto é, se fizermos F2/F1=1;
F3/F2=2; F4/F3=1,5; F5/F4=1,6;
F6/F5=1,6
Então os resultados das divisões
aproximam-se cada vez mais
de Phi, o número de ouro.

19. Com este trabalho aprendemos a
relação que existe entre a matemática
e a natureza. Aprendemos como os
coelhos se reproduzem e como a
matemática está envolvida em tudo o
que nos rodeia.
Esperamos que tenhamos sido
explícitos em toda a informação.

20. Trabalho realizado por:
Cristina Souto Nº6, 7ºA
Mariana Meireles Nº15, 7ºA
Pedro Rocha Nº20, 7ºA
Disciplina: Matemática 2001/2012
Professora: Anabela Tomé