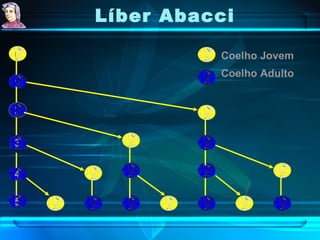
Leonardo Fibonacci foi um matemático italiano que publicou o livro Líber Abacci em 1202. O livro introduziu os algarismos hindus na Europa e continha o problema dos pares de coelhos, que demonstrava a sequência de Fibonacci. A sequência descreve o crescimento mensal de pares de coelhos e aparece em muitos outros fenômenos na natureza.

1. Universidade de Taubaté Departamento de Matemática e Física Eduardo d. Cursino Taubaté - SP 2010

2. Leonardo Pisano Fibonacci

3. Levando em consideração a pesquisa realizada, será demonstrado à biografia e um dos trabalhos deste grande matemático que foi Leonardo Fibonacci, considerando varias contextualizações de suas descobertas, com a pratica do que já existia, e também as que começaram com ele. Introdução

4. Fibonacci Leonardo de Pisa também conhecido como Fibonacci (filho de Bonaccio), nasceu em Pisa, centro comercial importante na Itália. Seu pai era comerciante e tinha negócios no norte da África. Assim Leonardo estudou com um professor muçulmano e viajou pelo Egito, Síria e Grécia, onde entrou em contato com os procedimentos matemáticos orientais, como os métodos algébricos árabes e os numerais indo-arábico. Ao retornar a sua terra natal, publicou sua obra mais famosa intitulada Líber Abacci (ou livro do Ábaco).

5. Líber Abacci Este livro foi publicado em 1202 e chegou até nós, graças à sua segunda edição de 1228. Este livro contém uma grande quantidade de assuntos relacionados com a Aritmética e Álgebra da época e realizou um papel importante no desenvolvimento matemático na Europa nos séculos seguintes, pois por este livro os europeus vieram a conhecer os algarismos hindus, também denominados arábicos. A teoria contida no livro Líber Abacci é ilustrada com muitos problemas que representam uma grande parte do livro.

6. Líber Abacci Um dos problemas que está nas páginas 123 e 124 deste livro é o Problema dos pares de coelhos (paria coniculorum): Quantos pares de coelhos podem ser gerados de um par de coelhos em um ano? Um homem tem um par de coelhos em um ambiente inteiramente fechado. Desejamos saber quantos pares de coelhos podem ser gerados deste par em um ano, se de um modo natural a cada mês ocorre à produção de um par e um par começa a produzir coelhos quando completa dois meses de vida.

7. Líber Abacci Como o par adulto produz um par novo a cada 30 dias, no início do segundo mês existirão dois pares de coelhos, sendo um par de adultos e outro de coelhos jovens, assim no início do 2º mês existirão 2 pares: 1 par adulto + 1 par recém nascido.

8. Líber Abacci No início do 3º mês o par adulto produzirá de novo mais um par enquanto que o par jovem terá completado 1 mês de vida e ainda não estará apto a produzir, assim no início do terceiro mês existirão três pares de coelhos, sendo: 1 par adulto + 1 par com 1 mês de idade + 1 par recém nascido.

9. Líber Abacci No início do 4º mês, existirão dois pares adultos sendo que cada um já produziu um novo par e um par novo que completou 1 mês, logo teremos 5 pares: 2 pares adultos + 1 par com 1 mês + 2 pares recém nascidos. No início do 5º mês, existirão três pares adultos sendo que cada um já produziu um novo par e dois pares novos que completaram 1 mês de vida, assim teremos 8 pares: 3 pares adultos + 2 pares (1 mês) + 3 pares recém nascidos.

10. Líber Abacci No início do 6º mês, existirão cinco pares adultos sendo que cada um já produziu um novo par e três pares novos que completaram 1 mês, assim existirão 13 pares: 5 pares adultos + 3 par com 1 mês + 5 pares recém nascidos. Tal processo continua através dos diversos meses até completar um ano.

11. Líber Abacci 0 2 3 4 5 1 Coelho Jovem Coelho Adulto

12. Líber Abacci Observa-se esta formação no gráfico com círculos, mas também se pode perceber que a sequência numérica, conhecida como a sequência de Fibonacci, indica o número de pares ao final de cada mês: {1, 1, 2, 3, 5, 8, 13, 21, 34,...} Esta sequência de números tem uma característica especial denominada recursividade:

13. Líber Abacci 1º.termo somado com o 2º.termo gera o 3º.termo 2º.termo somado com o 3º.termo gera o 4º.termo 3º.termo somado com o 4º.termo gera o 5º.termo Continua...

14. Líber Abacci Denotando a sequência por u=u(n) como o número de pares de coelhos ao final do mês n, poderemos escrever: u (1) + u (2) = u (3) u (2) + u (3) = u (4) u (3) + u (4) = u (5) u (4) + u (5) = u (6) que é uma propriedade recursiva, isto é, que cada termo pode ser obtido em função dos termos anteriores. No final do mês 12, o número de pares de coelhos deverá ser 144. Em geral, temos: u (n+1) = u (n-1) + u(n)

15. Aplicações Pergunta: Será que esta sequência numérica aparece em outras situações da vida? A resposta é positiva e pode-se apresentar uma grande quantidade de situações onde ela ocorre, abaixo veremos algumas.

16. Aplicações Estudo genealógico de coelhos (Visto na simulação) Estudo genealógico de abelhas Comportamento da luz Comportamento de átomos Crescimento de plantas Ascensão e queda em bolsas de valores Probabilidade e Estatística

17. Aplicações Curvas com a forma espiralada como: Nautilus (marinho), galáxias, chifres de cabras da montanha, marfins de elefantes, filotaxia, rabo do cavalo marinho, onda no oceano, furacão, etc.

18. Conclusão Fundamentando-se na seqüência apresentada e nas aplicações que são possíveis de se realizar com tal conceito, vê – se a praticidade e a evolução que foi possível após tal descoberta, tornado a vida mais pratica em muitos sentidos.

19. Referencias Bibliográfica http://pessoal.sercomtel.com.br/matematica/alegria/fibonacci/seqfib1.htm

20. Visitem http://eduardocursino.blogspot.com/