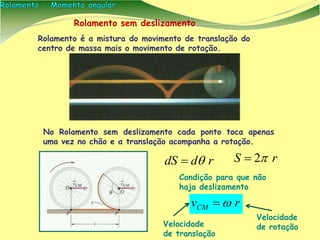
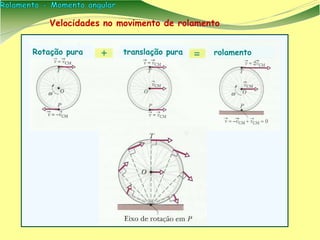
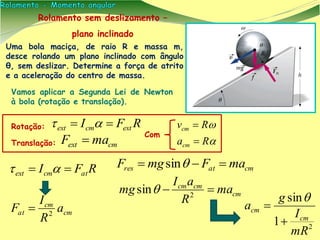
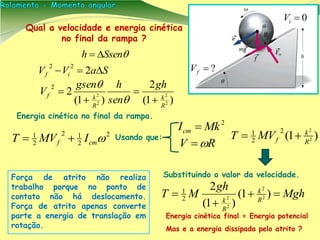
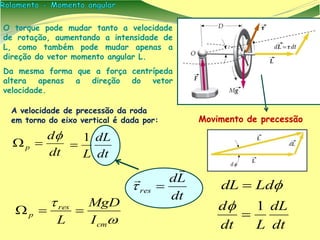
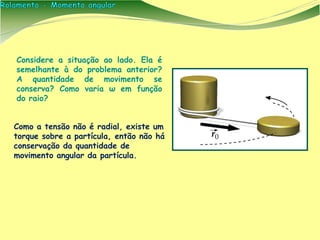
[1] O documento apresenta conceitos de física sobre rolamento e momento angular, que descrevem o movimento de objetos rolando sem deslizar. [2] É introduzido o conceito de momento angular como análogo à quantidade de movimento para rotações, e discutidas suas propriedades vetoriais. [3] São mostrados exemplos de cálculos envolvendo rolamento, incluindo de uma bola em uma rampa e de objetos rolando sem deslizar.

1. Física I para Oceanografia
FEP111 (4300111)
2º Semestre de 2011
Instituto de Física- Universidade de São Paulo
Aula – 10 Rolamento e momento angular
Professor: Valdir Guimarães
E-mail: valdir.guimaraes@usp.br
Fone: 3091.7104

2. Rolamento e momento angular
Rolamento descreve o movimento de carros, bicicletas e outros ...
Momento angular é um conceito útil para se entender a física das rotações.

3. Rolamento sem deslizamento
Rolamento é a mistura do movimento de translação do
centro de massa mais o movimento de rotação.
No Rolamento sem deslizamento cada ponto toca apenas
uma vez no chão e a translação acompanha a rotação.
Condição para que não
haja deslizamento
rvCM 
Velocidade
de translação
Velocidade
de rotação
rddS  rS 2

4. Velocidades no movimento de rolamento
Rotação pura translação pura rolamento

5. Dinâmica do rolamento
Sem atrito = deslizamento
Com atrito = rolamento
Portanto o atrito é a força
responsável pelo movimento de
rolamento.
rFI atritocmext  
cmext maF 
Com
racm 
Equação para rotação.
Equação para translação.
Quando temos atrito estático (sem deslizamento no ponto de contato)
se considera que não há perda de energia no sistema, ou seja, que o
sistema é conservativo. Isto é aproximadamente correto.

6.  Atrito estático
 Não há perda de energia
 Sistema conservativo.
ncmecext WEW 
cm
g
v
h icm
29
10
7 2

Não existem forças externas e nem forças internas dissipativas.
Energia Mecânica se conserva. 2
5
2
mRI 
Rolamento sem deslizamento
Exemplo: Uma bola de boliche, com 11 cm de raio e
7,2 kg, rola sem deslizar a 2,0 m/s . Ela continua a
rolar sem deslizar, ao subir uma rampa até a altura
h, quando atinge o repouso. Determine h.
00  mecE
iiff KUKU 
22
2
1
2
1
00 icmcm Imvmgh i


7. Uma bola maciça, de raio R e massa m,
desce rolando um plano inclinado com ângulo
θ, sem deslizar. Determine a força de atrito
e a aceleração do centro de massa.
RFI extcmext  
cmext maF  Com
Vamos aplicar a Segunda Lei de Newton
à bola (rotação e translação).


Ra
Rv
cm
cm


Rolamento sem deslizamento –
plano inclinado
cmatres maFmgF  sin
cm
cmcm
ma
R
aI
mg  2
sin
2
1
sin
mR
I
g
a
cm
cm



Translação:
Rotação:
RFI atcmext  
cm
cm
at a
R
I
F 2


8. anel
cilindro
esfera
Rolando de um plano inclinado, quem chegaria primeiro?
2
MkIntegenericame cm 
2
2
2 1
sin
1
sin
R
k
g
mR
I
g
a
cm
cm






 2
2
1
1
R
k
0.5 para anel
0.66 para cilindro
0.71 para esfera
Portanto esfera chega primeiro ! ! !
2
2
2
1
2
5
2
MRIanel
MRIcilindro
MRIesfera
cm
cm
cm




9. Qual seria o maior ângulo para que não houvesse deslizamento ?
RFI atcmext  
cm
cm
at a
R
I
F 2

2
MkIcm 
2
2
1
sin
R
k
g
acm



)(
)1(
22
2
2
22
2
2
kR
k
Mgsen
R
k
gsen
R
Mk
a
R
I
F cm
cm
at



 

Usando que:
Por outro lado:  cosMgNF eeat 
 cos
)( 22
2
Mg
kR
k
Mgsen e
 e
k
kR
tg  2
22
)( 

racm 

10. Qual a velocidade e energia cinética
no final da rampa ?
Ssenh 
SaVV if  2
22
0iV
?fV
)1(
2
)1(
2
2
2
2
2
2
R
k
R
kf
gh
sen
hgsen
V






2
2
12
2
1
cmf IMVT 
Energia cinética no final da rampa.
2
MkIcm 
RV 
Usando que: )1( 2
22
2
1
R
k
fMVT 
Mgh
gh
MT R
k
R
k


 )1(
)1(
2
2
2
2
22
1
Substituindo o valor da velocidade.
Energia cinética final = Energia potencial
Mas e a energia dissipada pelo atrito ?
Força de atrito não realiza
trabalho porque no ponto de
contato não há deslocamento.
Força de atrito apenas converte
parte a energia de translação em
rotação.

11. Bola de Sinuca
Um taco atinge uma bola de bilhar em um ponto a uma distância b acima do
centro da bola. Determine o valor de d para que a bola role, sem deslizar.
b
RFI extcmext  
cmext maF  Com


Ra
Rv
cm
cm


Translação:
Rotação:
inicialI _
Para rolamento sem deslizamento
Impulso inicial do taco:
t
P
F


 ifinicial MVMVPtFI 
cmMVtF  Taco dá uma velocidade inicial
de translação e rotação.
 cmIt 
b = parametro
de impacto

12. Rb 5
2

 cmIt 
2
5
2
MRIcm 
FbUsando que:
2
5
2
MRtFb 
2
5
2
MRtbF 
2
5
2
MRbMVcm 
cmMVtF 
22
5
R
bVcm

Sentido horário
torque negativo
RVcm Para que a bola
role sem deslizar 22
5
R
bR
 
Velocidade angular
no sentido horário
b
inicialI _
b = parametro
de impacto

13. Agora, vamos considerar os casos em que o eixo de rotação pode
alterar a sua direção. Isto explicita a natureza vetorial da rotação.
Definimos a direção do vetor velocidade angular como perpendicular
ao plano de rotação e o sentido dado pela regra da mão direita.
A natureza vetorial da rotação

14. A definição mais completa do torque é dada em termos do produto vetorial
Fr


A natureza vetorial do Torque
 Fsenr
Torque é um vetor perpendicular ao
plano formado pelos vetores r e F

15. Momento Angular
O momento angular desempenha o mesmo papel na rotação que o
momento linear desempenha na translação.
dt
prd
dt
pd
rFr
)(

 

vmp


Por analogia à quantidade
de movimento linear
podemos também escrever
Na translação temos:
am
dt
vd
m
dt
vmd
dt
pd
Fres



)(
definição de Newton para a sua segunda lei.
prL

Definimos a Quantidade de Movimento Angular (ou
Momento Angular) em relação à origem, como sendo




I
dt
Ld
segunda lei de Newton na rotação.

16. Momento Angular
A figura ao lado, mostra uma partícula
de massa m, na posição r, se movendo
com uma velocidade v. Ela possui uma
quantidade de movimento linear
prL


vmp


Definimos o Momento Angular em
relação à origem, como sendo

17. Momento Angular
prL


Por analogia à quantidade de movimento linear


IL 
Porém, se mudarmos a origem do sistema de
coordenadas, em relação ao plano da órbita,
obtemos um novo valor de L que não é paralelo a
ω.
Isto indica que a última definição não é universal.
prL


vmp


podemos também escrever

18. No entanto, se tivéssemos duas massas simétricas em relação ao
eixo z, L seria paralelo a ω.
Isto mostra que a última definição é válida apenas quando temos
simetria em relação ao eixo de rotação.
Momento Angular
prL




IL 

19. A segunda lei de Newton para a translação pode ser escrita como:
dt
pd
F sis
ext


Mais analogias
A segunda lei de Newton para a rotação pode ser escrita em
termos do torque e momento angular como:
dt
Ld sis
ext



Para corpos pequenos e partículas é mais prático usarmos:
Para corpos extensos girando usamos:
prL

 mvrL 


IL  IL 

20. momento de inércia (I)
de uma partícula
2
iirmI 
2
2
1
IK Energia Cinética Rotacional
Um corpo consiste de 4 partículas pontuais, com massas m, ligadas por
hastes sem massa, como na figura ao lado. O sistema gira com velocidade
angular ω em torno do centro do corpo. (a) Determine o momento de
inércia do corpo. (b) Determine a energia cinética do corpo.
 
i
iirmI 2
2
2
1
IK 
2
4maI 
22
2 maK 
Energia Cinética Rotacional

21. Vamos fixar o sistema de coordenadas no
eixo da polia, com o eixo z paralelo ao eixo
da polia.
Uma polia sem atrito nos mancais, tem dois
blocos, de massas m1 > m2, ligadas por um
fio de massa desprezível. A polia é disco de
massa M e raio R. Determine a aceleração dos
blocos.
Como os vetores torque, velocidade
angular e momento angular são paralelos
ao eixo z, podemos tratar este
problema, como unidimensional e
trabalhar escalarmente.
21 LLLL pz 
vRmvRmILz 21  
21 LLLL ptotal 
P2
P1
111 prL


vRmsenprL 1111  

22. vRmvRmILz 21  
aRmmI
dt
dL
ext )( 21  
Ra 
2
2
1 MRI 
g
Mmm
mm
a
2/21
21



dt
Ld
ext



aRmm
R
a
MRgRmgRm )( 21
2
2
1
21 
Usando que:
21 PPgnext  
gRmgRmext 21  P2
P1

23. O peso não gera torque
em relação ao eixo que
passa pelo centro de
massa.
Conservação do Momento Angular
Quando o torque externo resultante sobre um sistema é nulo, temos:
0
dt
Ld
ext


 cteLsis 

Assim para sistemas isolados e sem torque externo
temos a Conservação do Momento Angular do sistema.
fi LL 
ffii II  

24. Discos sobrepostos
O disco 1 gira livremente com velocidade
angular ωi. Seu momento de inércia é I1. Ele
cai sobre o disco 2, com momento de inércia
I2, que está em repouso. Devido ao atrito
cinético, os dois discos tendem a ter a
mesma velocidade. Determine ωf
0
dt
Ld
ext


 cteLL fi 
Temos a Conservação do Momento Angular do sistema.
fi III  )( 211 
if
II
I

21
1


ffii II  

25. Portanto, a Energia
Cinética não se conservou
e nem a energia mecânica.
Energia
Vamos verificar a conservação da energia
cinética
I
L
I
I
IK
22
)(
2
1 22
2



Podemos escrever a Energia Cinética de
Rotação como:
2
12
1
ii IK 
iif
II
I
II
I
IIK 2
21
2
1
2
122
21
1
212
1
)())(( 




21
1
II
I
K
K
i
f


if
II
I

21
1

ff IIK 2
212
1
)(  se

26. Como o torque externo em relação ao eixo do carrossel é nulo,
há conservação da quantidade de movimento angular
Um parque possui um pequeno carrossel de 3,0 m
de diâmetro e 130 kg.m2 de momento de inércia.
Cinco colegas se colocam próximo à borda, com o
carrossel girando a 20 rpm. Quatro dos colegas
se movam rapidamente para o centro do
carrossel (r= 30 cm). Se a aceleração centrípeta
necessária para atirar o quinto colega para fora
do carrossel é de 4g, determine se este foi
arremessado. (a massa de cada colega é 60 kg)
if LL  iiff II  
carri ImRI  2
5
2
.287 mkgI f 
2
.805 mkgIi 
carrf ImrmRI  22
4 sradrpmf /88,52,56 
gsmR
R
v
ac 5/9,51 22
2
 
Arremessado !
sradrpmi /09.20,20 

27. Como o torque externo em relação ao eixo do carrossel é nulo, há
conservação da quantidade de movimento angular
Uma criança de 25 kg, corre a 2,5 m/s,
tangente à borda de um carrossel de raio 2,0
m. O carrossel inicialmente em repouso, tem
momento de inércia de 500 kg.m2. A criança
pula sobre o carrossel. Determine a velocidade
angular final do conjunto.
if LL 
fff IL 
carrf ImRI  2 srad
ImR
Rmv
carr
i
f /21,02



iici RmvvmrL 

iff RmvI 

28. Como a tensão é radial, não realiza torque sobre a partícula, então há
conservação da quantidade de movimento angular da partícula.
Uma partícula de massa m se move sem atrito
com velocidade v0 em um círculo de raio r0. A
partícula está presa a um fio que passa por um
furo na mesa. O fio é puxado até que o raio do
movimento passe a ser rf.
(a) Determine a velocidade final.
(b) Determine a tensão no fio.
(c) Determine o trabalho realizado pela tensão
sobre a partícula.
if LL  00 vmrvmr ff


r
v
mT
2

f
f
r
vr
v 00

mrvL  3
2
mr
L
T 
a)
b)
00mvrmvr ff 

29. 3
2
mr
L
T 
 
ff r
r
r
r
dr
mr
L
TdrW
00
3
2








 2
0
2
2
11
2 rrm
L
W
f
c)
  TdrldFW


30. A mesma condição anterior, porém com o eixo da roda na horizontal.
Como fazer para colocar o eixo na vertical?
O que acontece com a cadeira?
Para pensar !
Uma pessoa está sobre uma cadeira giratória, com a roda de bicicleta com
seu eixo na vertical. Se ela gira a roda, o que acontece com a cadeira?

31. Roda de bicicleta
A “roda de bicicleta” vista na aula consiste em um
corpo em rotação chamado de giroscópio, com o
seu eixo livre para alterar a sua direção.
A quantidade de movimento angular da roda é:
dt
Ld





cmIL 
Aplicando-se a segunda lei de Newton para a rotação, temos:
gMrcmres


Giroscópio
Mas também
DMg
cmIL 
módulo

32. A velocidade de precessão da roda
em torno do eixo vertical é dada por:
O torque pode mudar tanto a velocidade
de rotação, aumentando a intensidade de
L, como também pode mudar apenas a
direção do vetor momento angular L.
Da mesma forma que a força centrípeda
altera apenas a direção do vetor
velocidade.
dt
Ld
res


 LddL 
dt
d
p




cm
res
p
I
MgD
L

Movimento de precessão
dt
dL
Ldt
d 1


dt
dL
L
1


33. A colisão é inelástica, não há conservação da energia mecânica do sistema.
Uma barra fina de massa M e comprimento d
está pendurada em um pivô. Um pedaço de massa
de modelar de massa m e velocidade v, atinge a
barra a uma distância x do pivô e se prende a
ela. Determine a razão entre as energias
cinéticas antes e depois da colisão.
mvxvmrLf 

2
2
1
mvKi 
22
3
1
MdmxI f 
f
f
fff
I
L
IK
22
1
2
2
 

34. if LL  mvxvmrLL if 

2
2
1
mvKi 
)3(
)(
2
3
22
2
Mdmx
mvx
K f


f
f
fff
I
L
IK
22
1
2
2
 
2
2
3
1
1
mx
MdK
K
i
f


Durante a colisão há uma grande força no pivô, portanto não há
conservação da quantidade de movimento linear.
A força no pivô é radial, não existe torque e temos conservação
da quantidade de movimento angular.
2
22
2
2
1
)3(
)(
2
3
mv
Mdmx
mvx
K
K
i
f 


35. Como a tensão não é radial, existe um
torque sobre a partícula, então não há
conservação da quantidade de
movimento angular da partícula.
Considere a situação ao lado. Ela é
semelhante à do problema anterior?
A quantidade de movimento se
conserva? Como varia ω em função
do raio?