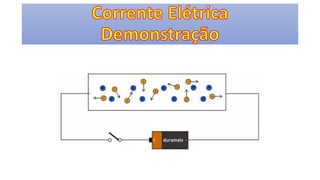
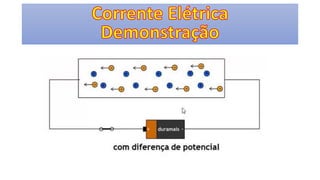
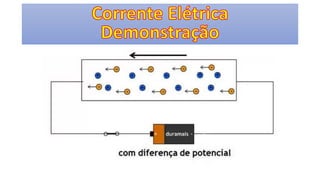
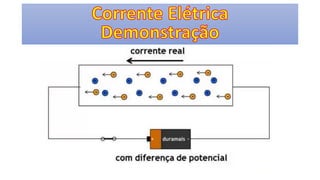
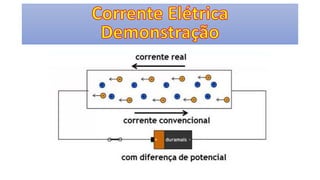
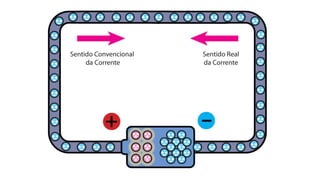
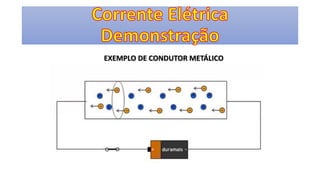
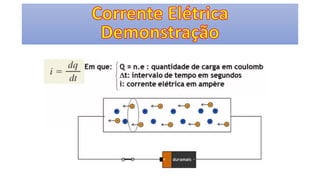
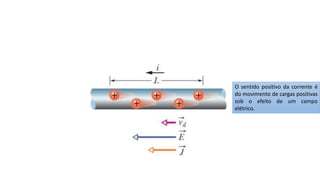
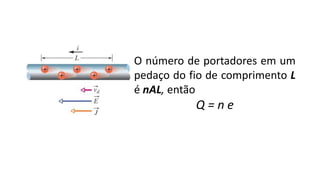
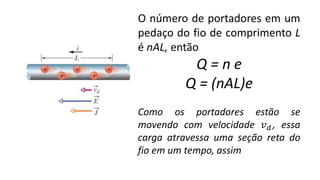
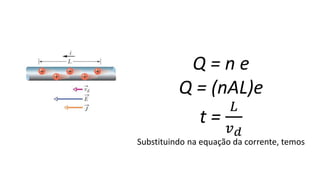
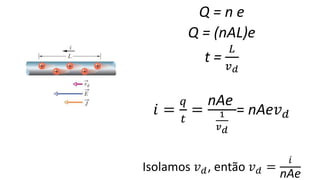
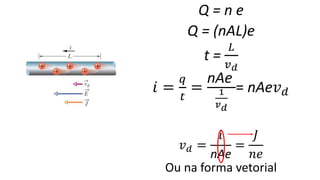
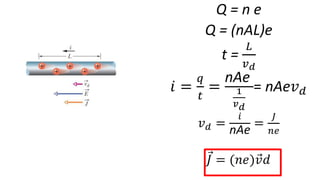
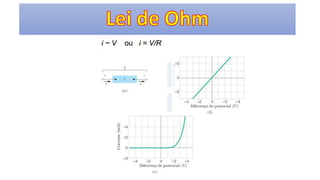
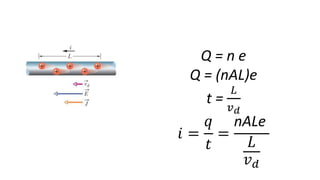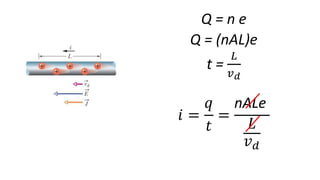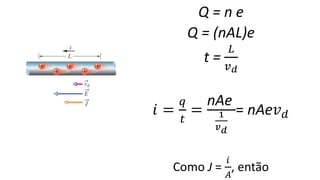O documento descreve os conceitos fundamentais de corrente elétrica, incluindo que é o movimento ordenado de elétrons em um condutor quando submetido a um campo elétrico, e que a intensidade de corrente é definida como o fluxo de cargas por unidade de tempo atravessando uma seção do condutor. Também apresenta a lei de Ohm, relacionando corrente, tensão e resistência.

3. • É o movimento ordenado de partículas portadoras de
cargas elétricas. Microscopicamente as cargas livres
estão em movimento aleatório em razão da agitação
térmica. No entanto, se aplicarmos um campo elétrico
na região das cargas é possível observar que elas
passam a ter movimento ordenado. Esse movimento
se chama movimento de deriva de cargas livres.

4. • Sabemos que os materiais condutores se caracterizam pelo fato de
possuírem elétrons que são fracamente ligados a seus átomos e por
essa razão são chamados de elétrons livres;
• Se esse condutor não estiver submetido a uma DDP, podemos
observar que esses elétrons estão em um movimento desordenado,
de tal maneira que não existe um fluxo continuo de elétrons em uma
determinada direção;
• Esses elétrons podem saltar de um átomo a outro sem seguir um
fluxo determinado;
• Se fecharmos o circuito iremos submeter o condutor a uma DDP;
• Os elétrons tendem a se deslocar do menor para o maior potencial;

12. • Chamamos de corrente elétrica ao movimento de
portadores de carga, que nos sólidos são os elétrons;
• Nos gases e líquidos, além dos elétrons, se
movimentam também íons negativos e positivos;
• Definimos a intensidade de corrente elétrica como
sendo o fluxo de portadores de cargas por unidade de
tempo que passa por uma sessão transversal do
condutor.

13. EXEMPLO DE CONDUTOR METÁLICO

14. EXEMPLO DE CONDUTOR METÁLICO

16. • Corrente Contínua:
É aquela em que o sentido dos portadores de cargas é invariável -
mesmo sentido, eles continuam o movimento com o mesmo sentido.
• Corrente Alternada:
É aquela em que o sentido dos portadores de cargas é variável, ou
seja, podem se movimentar para um lado ou para o outro.

18. • Para descrever o fluxo de cargas, usamos a densidade de
corrente 𝒋;
• Tem a mesma direção e sentido que a velocidade das cargas
da corrente;
• Se as cargas forem positivas e a mesma direção;
• E o sentido oposto se as cargas forem negativas.
• Para cada elemento da sessão reta, o modulo j é igual à
corrente divida pela área do elemento.

19. • Podemos escrever a corrente que atravessa o elemento de área como
𝑱 . 𝒅𝑨, onde 𝒅𝑨 é o vetor área do elemento, perpendicular ao
elemento.
i = 𝑱. 𝒅𝑨

20. • Podemos escrever a corrente que atravessa o elemento de área como
𝑱 . 𝒅𝑨, onde 𝒅𝑨 é o vetor área do elemento, perpendicular ao
elemento.
i = 𝐽. 𝑑 𝐴
Se a corrente é uniforme em toda superfície e paralela a 𝒅𝑨, 𝑱 também
é uniforme e paralela a 𝒅𝑨, assim

21. • Podemos escrever a corrente que atravessa o elemento de área como
𝑱 . 𝒅𝑨, onde 𝒅𝑨 é o vetor área do elemento, perpendicular ao
elemento.
i = 𝐽. 𝑑 𝐴
i = 𝐽 𝑑𝐴 = 𝐽 𝑑𝐴 = 𝐽𝐴
Então,

22. • Podemos escrever a corrente que atravessa o elemento de área como
𝑱 . 𝒅𝑨, onde 𝒅𝑨 é o vetor área do elemento, perpendicular ao
elemento.
i = 𝐽. 𝑑 𝐴
i = 𝐽 𝑑𝐴 = 𝐽 𝑑𝐴 = 𝐽𝐴
J =
𝑖
𝐴

23. • Quando um condutor não está sendo percorrido por corrente, os
elétrons se movem aleatoriamente, sem que haja uma direção
preferencial.
• Quando existe uma corrente, os elétrons continuam a se mover
aleatoriamente, mas tendem a derivar com uma velocidade de deriva
𝑣 𝑑 no sentido oposto ao do campo elétrico que produziu a corrente.
• A velocidade deriva é muito pequena em relação à velocidade em que
os elétrons se movem aleatoriamente.

24. O sentido positivo da corrente é
do movimento de cargas positivas
sob o efeito de um campo
elétrico.

25. O número de portadores em um
pedaço do fio de comprimento L
é nAL, então
Q = n e

26. O número de portadores em um
pedaço do fio de comprimento L
é nAL, então
Q = n e
Q = (nAL)e
Como os portadores estão se
movendo com velocidade 𝑣 𝑑 , essa
carga atravessa uma seção reta do
fio em um tempo, assim

27. Q = n e
Q = (nAL)e
t =
𝐿
𝑣 𝑑
Substituindo na equação da corrente, temos

28. Q = n e
Q = (nAL)e
t =
𝐿
𝑣 𝑑
𝑖 =
𝑞
𝑡
=
nALe
𝐿
𝑣 𝑑

29. Q = n e
Q = (nAL)e
t =
𝐿
𝑣 𝑑
𝑖 =
𝑞
𝑡
=
nALe
𝐿
𝑣 𝑑

30. Q = n e
Q = (nAL)e
t =
𝐿
𝑣 𝑑
𝑖 =
𝑞
𝑡
=
nAe
1
𝑣 𝑑
= nAe𝑣 𝑑

31. Q = n e
Q = (nAL)e
t =
𝐿
𝑣 𝑑
𝑖 =
𝑞
𝑡
=
nAe
1
𝑣 𝑑
= nAe𝑣 𝑑
Como J =
𝑖
𝐴
, então

32. Q = n e
Q = (nAL)e
t =
𝐿
𝑣 𝑑
𝑖 =
𝑞
𝑡
=
nAe
1
𝑣 𝑑
= nAe𝑣 𝑑
Isolamos 𝑣 𝑑, então 𝑣 𝑑 =
𝑖
nAe

33. Q = n e
Q = (nAL)e
t =
𝐿
𝑣 𝑑
𝑖 =
𝑞
𝑡
=
nAe
1
𝑣 𝑑
= nAe𝑣 𝑑
𝑣 𝑑 =
𝑖
nAe
=
𝐽
𝑛𝑒
Ou na forma vetorial

34. Q = n e
Q = (nAL)e
t =
𝐿
𝑣 𝑑
𝑖 =
𝑞
𝑡
=
nAe
1
𝑣 𝑑
= nAe𝑣 𝑑
𝑣 𝑑 =
𝑖
nAe
=
𝐽
𝑛𝑒
𝐽 = (𝑛𝑒) 𝑣𝑑

36. • Resistência: é uma medida do quanto um material resiste à passagem
de cargas nele.
• Medida em Ohms pela letra ômega (Ω);
• Quando em um circuito, um condutor tem função de introduzir uma
certa resistência ele é denominado resistor.
• Resistividade: é o modulo do campo elétrico num elemento de
circuito.
R Resistencia 𝜴
V Potencial V
i Corrente A
𝝆 Resistividade 𝜴m
E Campo elétrico V/m
J Densidade decorrente A/𝒎 𝟐

37. ATENÇÃO!!!!!!!
A RESISTENCIA É UMA PROPRIEDADE DE UM
DISPOSITIVO;
A RESISTIVIDADE É UMA PROPRIEDADE DE UM
MATERIAL.

38. • A condutividade é o inverso da Resistividade, assim
𝝈 =
𝟏
𝝆
𝝈 condutividade 𝜴𝒎−𝟏
𝝆 resistividade 𝜴𝒎

40. •É a afirmação de que a corrente que
atravessa um dispositivo é sempre
diretamente proporcional à diferença de
potencial aplicada ao dispositivo.

42. • Um dispositivo obedece à lei de Ohm se a resistência do dispositivo
não depende do valor absoluto nem da polaridade da diferença de
potencial aplicada.
• Um material obedece à lei de Ohm se a resistividade do material não
depende do módulo nem da direção do campo elétrico aplicado.

44. • Verificar a lei de Ohm nos processos de condução de eletricidade a
nível atômico;
• Analise no modelo de elétrons livres;
• Física Clássica: os elétrons possuem destruição de velocidades como
a de moléculas de um gás e essa velocidade depende da
temperatura;
• Os elétrons não são governados pelas lei da Física Clássica, mas pelas
leis da Física Quântica;
• Quando consideramos todos elétrons livres, a média dos movimentos
aleatórios é ZERO e não contribui para a velocidade de deriva.
• A velocidade de deriva se deve apenas ao efeito do campo elétrico
sobre os elétrons.

46. • Pela Segunda lei de newton temos:
𝑎 =
𝐹
𝑚

47. • Pela Segunda lei de newton temos:
𝑎 =
𝐹
𝑚
F = Ee, então...

48. • Pela Segunda lei de newton temos:
𝑎 =
𝐹
𝑚
=
𝑒𝐸
𝑚
Os elétrons passam a se mover em uma direção aleatória após cada
colisão. No intervalo de tempo médio 𝝉, assim um elétron adquire
velocidade de deriva 𝒗 𝒅 = 𝒂𝝉, então...

49. • Pela Segunda lei de newton temos:
𝑎 =
𝐹
𝑚
=
𝑒𝐸
𝑚
𝑣 𝑑 = 𝑎𝜏 =
𝑒𝐸𝜏
𝑚
Como 𝑱 = 𝒏𝒆𝒗 𝒅, então...

50. • Pela Segunda lei de newton temos:
𝑎 =
𝐹
𝑚
=
𝑒𝐸
𝑚
𝑣 𝑑 = 𝑎𝜏 =
𝑒𝐸𝜏
𝑚
𝑣 𝑑 =
𝐽
𝑛𝑒
=
𝑒𝐸𝜏
𝑚
Podendo ser escrita na forma...

51. • Pela Segunda lei de newton temos:
𝑎 =
𝐹
𝑚
=
𝑒𝐸
𝑚
𝑣 𝑑 = 𝑎𝜏 =
𝑒𝐸𝜏
𝑚
𝑣 𝑑 =
𝐽
𝑛𝑒
=
𝑒𝐸𝜏
𝑚
𝐸 =
𝑚
𝑒2 𝑛𝜏
J
Como 𝑬 = 𝝆 𝒋, obtemos...

52. • Pela Segunda lei de newton temos:
𝑎 =
𝐹
𝑚
=
𝑒𝐸
𝑚
𝑣 𝑑 = 𝑎𝜏 =
𝑒𝐸𝜏
𝑚
𝑣 𝑑 =
𝐽
𝑛𝑒
=
𝑒𝐸𝜏
𝑚
𝐸 =
𝑚
𝑒2 𝑛𝜏
J
𝜌 =
𝑚
𝑒2 𝑛𝜏