1) O documento discute métodos quantitativos aplicados à logística de distribuição, incluindo modelos analógicos e de programação linear.
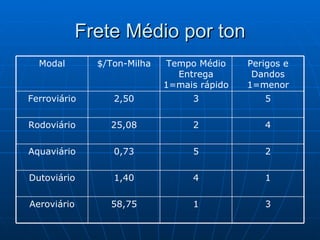
2) Os custos logísticos representam entre 15-25% do PIB de um país emergente, sendo transporte o principal fator.
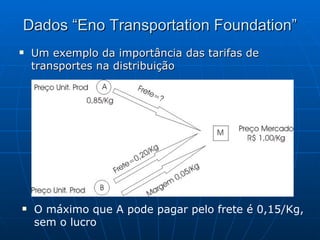
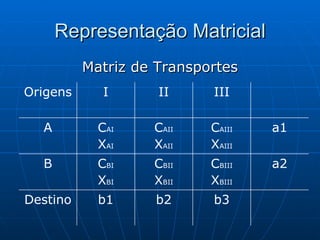
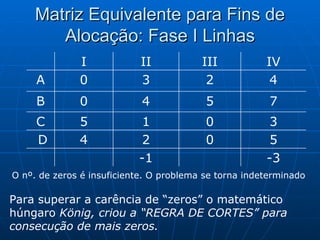
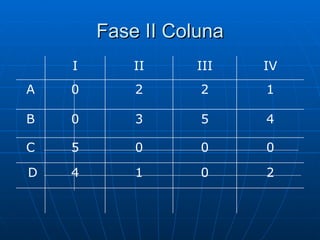
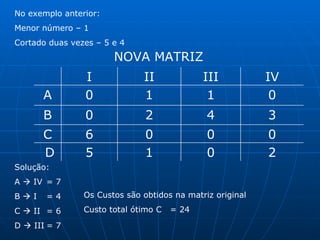
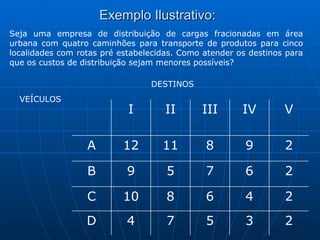
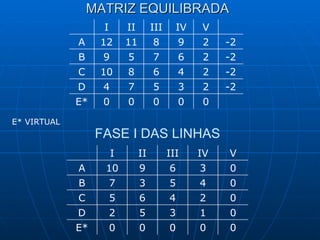
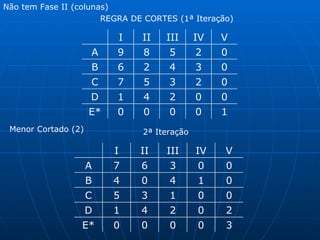
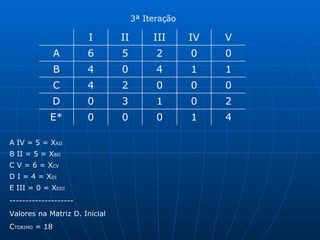
3) Métodos como regra do noroeste, custo mínimo e Vogel são abordados para alocar quantidades de forma a minimizar custos totais.













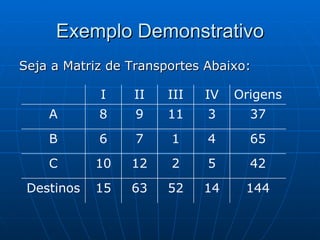



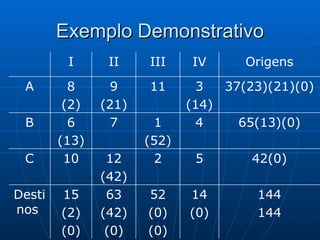





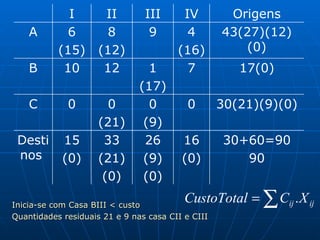

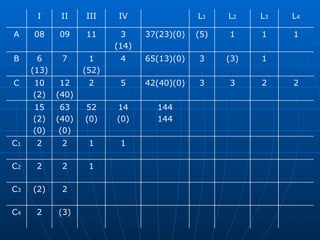



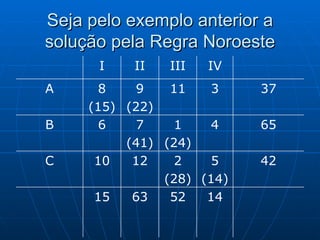





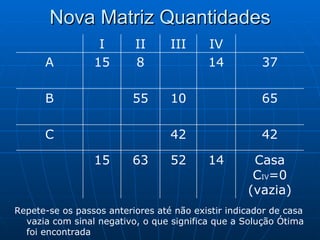








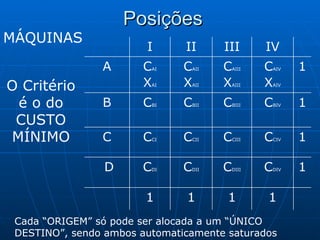
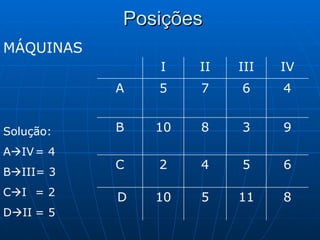

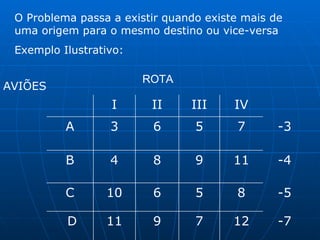





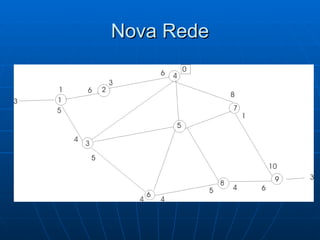
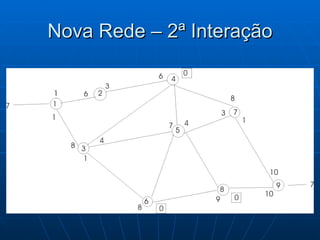
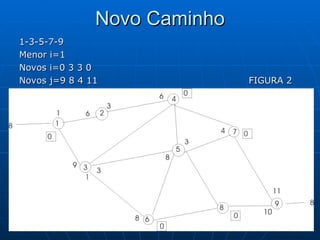
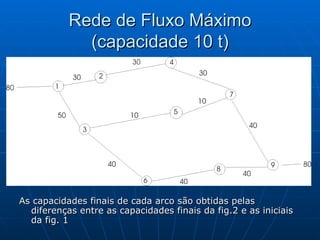
![Algoritmo de Dijkstra Seja a rede onde se deseja ir de 1 à 9 percorrendo o caminho mais curto Começamos com o Nó 1 rotulando de [0;0] porque não tem outros antes dele. A partir dele podemos ir para 2 ou 3 [1;3], saindo do Nó 1 e dura 4, idem para [1;4] e assim por diante. Caminho mais curso: 1 3 6 8 9 com distância de 12 und [8;12]](https://image.slidesharecdn.com/ibrahimfinal-100521172946-phpapp02/85/Metodos-Quantitativos-Aplicados-a-Logistica-68-320.jpg)

![OBRIGADO!!! Prof. Adm. Roberto Ibrahim Uehbe [email_address]](https://image.slidesharecdn.com/ibrahimfinal-100521172946-phpapp02/85/Metodos-Quantitativos-Aplicados-a-Logistica-70-320.jpg)