Este documento discute conceitos fundamentais de dinâmica de sistemas mecânicos. Aborda tópicos como geometria de massas, equações diferenciais, componentes energéticas, teoremas dinâmicos e análise de movimentos básicos. Também apresenta sistemas de um e dois graus de liberdade, sistemas contínuos como cordas, barras e vigas, além de métodos aproximados para resolução de problemas de vibração.

1. 1
Contents
Geometria de Massas ...............................................................................................................................................3
Conversões e Relações Trigonométricas ...................................................................................................................5
Equações Diferenciais – Nomenclatura .....................................................................................................................5
Componentes Energéticas .......................................................................................................................................6
Teoremas e Princípios Dinâmicos e Cinemáticos ......................................................................................................6
Sistemas Particulares................................................................................................................................................7
a) Análise de Movimentos Básicos.....................................................................................................................7
b) Análise de Roldanas (Pulley Systems) ............................................................................................................8
1- Sistemas c/ 1 Grau Liberdade .........................................................................................................................10
1.1- Introdução ..............................................................................................................................................10
1.2- Regime Livre (Equação Diferencial Ordinária Linear Homogênea)............................................................11
1.2.1- Sistema Subamortecido , 𝟎 ≤ 𝝃 < 𝟏...................................................................................................11
1.2.2- Resposta do Sistema Criticamente Amortecido , 𝝃 = 𝟏.....................................................................12
1.2.3- Resposta do Sistema Sobreamortecido , 𝝃 > 𝟏 .................................................................................12
1.3- Regime Forçado Periódico - Harmônico (E.D.L.O.N.) ................................................................................13
1.4.1- Solicitação Harmónica Ativa - Força Discreta.......................................................................................13
1.4.2 - Solicitação Harmónica Ativa – Rotação de Massas em Desiquilibrio ...................................................15
1.4.3- Solicitação Harmónica Passiva..............................................................................................................16
1.4.4- Isolamento de Vibrações ......................................................................................................................17
1.4.5- Transdutor de Vibrações .......................................................................................................................18
1.4- Regime Forçado Periódico - Não Harmônico............................................................................................19
1.5- Regime Forçado Não Periódico (Impulsiva e transiente) ..........................................................................20
1.7.1- Regime Forçado Impulsivo....................................................................................................................20
1.7.2- Regime Forçado Transiente ..................................................................................................................20
2 - Graus de Liberdade............................................................................................................................................22
2.1 – Introdução .................................................................................................................................................22
2.2 – Regime Livre ( Sistemas Não Amortecidos).................................................................................................23
2.3- Regime Forçado Harmônico.........................................................................................................................24
2.3.1 – Introdução...........................................................................................................................................24
2.4.2 – Absorsor de Vibrações.........................................................................................................................24
2.5 – Regime Forçado Transiente ........................................................................................................................27
3- Sistemas Contínuos.............................................................................................................................................28

2. 2
3.1- Vibração Lateral de Cordas...........................................................................................................................28
3.2- Vibração Longitudinal de Barras..................................................................................................................29
3.3- Vibração Torsional de Veios ........................................................................................................................30
3.4- Vibração lateral de Vigas..............................................................................................................................31
3.5- Metodo Aproximado da Energia de Rayleigh................................................................................................33
3.5.1 – Procedimento......................................................................................................................................33
3.6 – Considerações Práticas – Casos Particulares ...............................................................................................35
3.6.1- Resolução Analítica do Problema Característico..................................................................................35
3.6.2- Método de Rayleigh..............................................................................................................................39

3. 3
Geometria de Massas
Nomenclatura:
• Momento de 2ª ordem de área - 𝐼′ 𝑥𝑥 , 𝐼′ 𝑦𝑦 , 𝐼′ 𝑧𝑧 [𝑚4
]
• Momento Polar de Área - 𝐼 𝑝 = 𝐼𝑥𝑥 + 𝐼 𝑦𝑦
• Momento de Inércia de massas - 𝐼𝑥𝑥 , 𝐼 𝑦𝑦 , 𝐼𝑧𝑧 [𝑘𝑔 𝑚2
]
• Momento Polar de Inércia de massas - 𝐽 𝑜 = 𝐼 𝑝 𝜌𝑙 (válido para solidos sem desenvolvimento axial !! )
Solido Propriedade - Aplicação
Barra
Esbelta
(Secção
Qualquer)
Cinemática de Massas:
𝐼𝑧𝑧 =
𝑚𝐿2
12
Anel fino
Cinemática de Massas:
𝐼𝑧𝑧 = 𝐽 𝑜 =
𝑚𝑟2
2
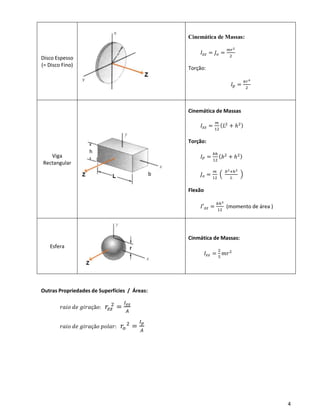
Varão Espesso
Cinemática de Massas:
𝐼 𝑦𝑦 = 𝐼𝑧𝑧 =
𝑚
12
(3𝑟2
+ 𝐿2)
Torção:
𝐼 𝑝 =
𝜋𝑟4
2
(momento polar de área)
𝐽 𝑜 = 𝐼𝑥𝑥 =
𝑚𝑟2
2
Flexão:
𝐼′ 𝑧𝑧 =
𝜋𝑟4
4
(momento de área )

4. 4
Disco Espesso
(= Disco Fino)
Cinemática de Massas:
𝐼𝑧𝑧 = 𝐽 𝑜 =
𝑚𝑟2
2
Torção:
𝐼 𝑝 =
𝜋𝑟4
2
Viga
Rectangular
Cinemática de Massas
𝐼𝑧𝑧 =
𝑚
12
( 𝐿2
+ ℎ2)
Torção:
𝐼 𝑃 =
𝑏ℎ
12
( 𝑏2
+ ℎ2)
𝐽 𝑜 =
𝑚
12
(
𝑏2+ℎ2
𝐿
)
Flexão
𝐼′ 𝑧𝑧 =
𝑏ℎ3
12
(momento de área )
Esfera
Cinmática de Massas:
𝐼𝑧𝑧 =
2
5
𝑚𝑟2
Outras Propriedades de Superfícies / Áreas:
𝑟𝑎𝑖𝑜 𝑑𝑒 𝑔𝑖𝑟𝑎çã𝑜: 𝑟𝑧𝑧
2
=
𝐼 𝑧𝑧
𝐴
𝑟𝑎𝑖𝑜 𝑑𝑒 𝑔𝑖𝑟𝑎çã𝑜 𝑝𝑜𝑙𝑎𝑟: 𝑟𝑜
2
=
𝐼 𝑝
𝐴
h
b

5. 5
Conversões e Relações Trigonométricas
• 𝜔 = 𝑟𝑝𝑚 ⋅ π
30
𝜔 = 2𝜋 ⋅ 𝑓𝐻𝑧 𝜔 =
2𝜋
𝑇
𝑓 =
1
𝑇
• 𝑟𝑎𝑑 = 𝛼° ⋅
π
180
𝛼° = 𝑟𝑎𝑑 ⋅
180
π
• sin( 𝜔𝑡) = cos (𝜔𝑡 −
𝜋
2
) − sin( 𝜔𝑡) = cos (𝜔𝑡 +
𝜋
2
) − cos( 𝜔𝑡) = cos( 𝜔𝑡 + 𝜋)
• Agrupamento de funções trignométricas de igual frequência (projeção no eixo dos xx):
Equações Diferenciais – Nomenclatura
𝛼
𝛼
Homogêneas
Não Homogêneas
Lineares
Não Lineares
𝑎 𝑛 𝑦 𝑛
𝑦 + 𝑎𝑦𝑦3
= 𝑘
Ordinárias
𝑎 𝑛 𝑦 𝑛
+ 𝑎 𝑛−1 𝑦 𝑛−1
+ ⋯ + 𝑎1 𝑦 + 𝑎0 = 0
de Derivadas Parciais
𝑎2
𝑑2
𝑑𝑥2 𝑢 + 𝑎1
𝑑
𝑑𝑥
𝑢 + 𝑏2
𝑑2
𝑑𝑡2 𝑢 + 𝑏1
𝑑2
𝑑𝑡
𝑢 + 𝑘 𝑜 = 𝐹
Equações Algébricas
Equações Diferenciais

6. 6
Componentes Energéticas
• Variação Energia Potencial: 𝑉 = ∑ 𝑚 𝑖 𝑔 (ℎ 𝐺 𝑖
|1 − ℎ 𝐺 𝑖
|0)𝑛
𝑖 + ∑
𝑘
2
[ ( 𝑥2 − 𝑥1)2
|1 − ( 𝑥2 − 𝑥1)2
|0 ]𝑁
𝑗
• Variação Energia Cinética 𝑇 = ∑
𝑚
2
(𝑥̇ 𝐺
2
|1 − 𝑥̇ 𝐺
2
|0) +
𝐽
2
(𝜃̇ 2
|1 − 𝜃̇ 2
|0)𝑛
𝑖
𝑇 = ∑
𝑚 𝑖
2
( 𝑥̇ 𝐺
2
) +
𝐽 𝑖
2
( 𝜃̇ 2
)𝑛
𝑖
• Teorema da Variação da 𝛥𝐸 𝑚𝑒𝑐 = 𝑊𝑓𝑛𝑐 = 𝑊𝑑𝑖𝑠𝑠𝑖𝑝 =
𝑘 𝑒𝑞
2
[ 𝑥𝑡̅
2
− 𝑥0
2
] +
𝑚 𝑒𝑞
2
[ 𝑥̇ 𝑡̅
2
− 𝑥̇0
2
]
Energia Mecânica (TVEM):
( 𝑊𝑓𝑛𝑐 = 𝑊𝑑𝑖𝑠𝑠𝑖𝑝 valido para regime livre ou natural)
• Definição de energia Dissipada: 𝑊𝑑𝑖𝑠𝑠𝑖𝑝 = ∫ 𝐹𝑐( 𝑡) ⋅ 𝑣( 𝑡)1 + 𝐹𝑐(𝑡) ⋅ 𝑣(𝑡)2 𝑑𝑡
𝑡2
𝑡1
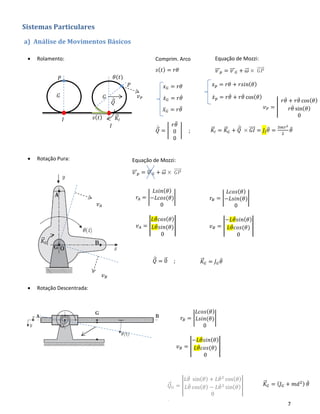
Teoremas e Princípios Dinâmicos e Cinemáticos
• Equação de Mozzi: 𝑣 𝑝⃗⃗⃗⃗ = 𝑣𝑜⃗⃗⃗⃗ + 𝜔⃗⃗ × 𝑂𝑃⃗⃗⃗⃗⃗
• Quantidade de Aceleração: 𝑄⃗̇
= 𝑚𝑣̇ = 𝑚𝑥̈
• Momento Dinâmico: 𝐾𝐺
⃗⃗⃗⃗⃗ = 𝐽 𝐺 ⋅ 𝜃̈
• 2º Teorema de König: 𝐾 𝑂
⃗⃗⃗⃗⃗ = 𝐾 𝐺
⃗⃗⃗⃗⃗ + 𝑂𝐺⃗⃗⃗⃗⃗ × 𝑄⃗̇
• Teorema de Steiner ou
Teorema dos Eixos Paralelos: 𝐽 ′
= 𝐽 + 𝑚𝑑2
Para momentos de Inércia
de 2ª ordem
• Teorema de Steiner 𝐾𝑜 = 𝐽 𝑜 𝜃̈ = ( 𝐽 𝐺 + 𝑚𝑑2 ) 𝜃̈
Momento Dinâmico:
• Força Impulsiva: 𝐹 = ∫ 𝑓(𝑡) 𝑑𝑡
0+𝛥𝑡
0
= 𝑚𝑥̇0 [N/s]
• Produto Interno Nulo: 𝑢 ⋅ 𝑣 = 0 ⇒ 𝑢 ⊥ 𝑣
• Produto Externo Nulo: 𝑢 × 𝑣 = 0 ⇒ 𝑢 ∥ 𝑣
Instante 0 de referência :
• Equilíbrio Estático
(T=0)
• As molas podem apresentar
pré-tensão
(V elástica=V gravítica) ou não
(V elástica = 0). Apenas serve
para anular a componente da
energia gravítica ou não, mas
nunca é calculada
• Sistemas tipo pêndulo (SEM
pré-tensão nas molas ) é que
apresentam variação da energia
potencial gravítica
válido apenas para pontos G
e O sem movimento relativo

7. 7
Sistemas Particulares
a) Análise de Movimentos Básicos
• Rolamento:
𝐾⃗⃗ 𝐼 = 𝐾⃗⃗ 𝐺 + 𝑄⃗̇
× 𝐺𝐼⃗⃗⃗⃗ = 𝐽𝐼 𝜃̈ =
3𝑚𝑟2
2
𝜃̈
• Rotação Pura:
• Rotação Descentrada:
𝜃(𝑡)
𝐼
𝐼 𝑠( 𝑡)
Comprim. Arco
𝑠( 𝑡) = 𝑟𝜃
𝑥 𝐺 = 𝑟𝜃
𝑥̇ 𝐺 = 𝑟𝜃̇
𝑥̈ 𝐺 = 𝑟𝜃̈
Equação de Mozzi:
𝑣⃗⃗⃗ 𝑝 = 𝑣⃗⃗⃗ 𝐺 + 𝜔⃗⃗ × 𝐺𝑃⃗⃗⃗⃗⃗
𝐺
𝑃
𝑥 𝑝 = 𝑟𝜃 + 𝑟𝑠𝑖𝑛( 𝜃)
𝑥̇ 𝑝 = 𝑟𝜃̇ + 𝑟𝜃̇ cos( 𝜃)
𝑣 𝑃 = |
𝑟𝜃̇ + 𝑟𝜃̇ cos( 𝜃)
𝑟𝜃̇ sin( 𝜃)
0
𝑃
𝐺
𝑄⃗̇
𝑣 𝑃
𝑄⃗̇ = |
𝑟𝜃̈
0
0
| ;
Equação de Mozzi:
𝑣⃗⃗⃗ 𝑝 = 𝑣⃗⃗⃗ 𝐺 + 𝜔⃗⃗ × 𝐺𝑃⃗⃗⃗⃗⃗
𝐾⃗⃗ 𝐼
𝑄⃗̇ = 0⃗ ;
𝐾⃗⃗ 𝐺
𝑟𝐴 = |
𝐿𝑠𝑖𝑛( 𝜃)
−𝐿𝑐𝑜𝑠(𝜃)
0
| 𝑟𝐵 = |
𝐿𝑐𝑜𝑠( 𝜃)
−𝐿𝑠𝑖𝑛(𝜃)
0
|
𝑣 𝐴 = |
𝐿𝜃̇ 𝑐 𝑜𝑠( 𝜃)
𝐿𝜃̇ 𝑠 𝑖𝑛(𝜃)
0
| 𝑣 𝐵 = |
−𝐿𝜃̇ 𝑠 𝑖𝑛( 𝜃)
𝐿𝜃̇ 𝑐 𝑜𝑠(𝜃)
0
|
𝐾⃗⃗ 𝐺 = 𝐽 𝐺 𝜃̈
𝑟𝐵 = |
𝐿𝑐𝑜𝑠( 𝜃)
𝐿𝑠𝑖𝑛(𝜃)
0
|
𝑣 𝐵 = |
−𝐿𝜃̇ 𝑠 𝑖𝑛( 𝜃)
𝐿𝜃̇ 𝑐 𝑜𝑠(𝜃)
0
|
𝑣 𝐴
𝑣 𝐵
𝑄⃗ 𝐺
̇ = |
𝐿𝜃̈ sin( 𝜃) + 𝐿𝜃̇2
cos( 𝜃)
𝐿𝜃̈ cos( 𝜃) − 𝐿𝜃̇2
sin( 𝜃)
0
|
;
𝐾⃗⃗ 𝐺 = ( 𝐽 𝐺 + 𝑚𝑑2) 𝜃̈

8. 8
b) Análise de Roldanas (Pulley Systems)
Princípio base: Pulley Length Equations Constrain - 𝐿 = 𝐶 𝑡𝑒
= ∑ 𝑠𝑖𝑗 + ∑ 𝑐𝑖𝑖 → ∆𝐿 = 0 = ∆𝑆𝑖
∆𝑆𝑙𝑎𝑑𝑜 𝑑𝑖𝑟𝑒𝑖𝑡𝑜 = ∆𝑆𝑙𝑎𝑑𝑜 𝑒𝑠𝑞𝑢𝑒𝑟𝑑𝑜
Análise Válida quando numa roldana móvel há diminuição do comprimento de corda em ambos os lados
• Capacidade
de manter
suspensa a
carga
• Desmultiplicação
de Forças
𝑠(𝑡)
𝑠(𝑡)
EDM:
𝑚 𝑥̈ = (2𝑇 − 𝑚𝑔)
𝑥( 𝑡) =
𝑠(𝑡)
2
𝑥̇( 𝑡) =
𝑠̇( 𝑡)
2
𝑥̈( 𝑡) =
𝑠̈( 𝑡)
2
EDM:
𝑚 𝑥̈ = (3𝑇 − 𝑚𝑔)
𝑥( 𝑡) =
𝑠(𝑡)
3
𝑥̇( 𝑡) =
𝑠̇( 𝑡)
3
𝑥̈( 𝑡) =
𝑠̈( 𝑡)
3
EDM:
𝑚 𝑥̈ = (4𝑇 − 𝑚𝑔)
𝑥( 𝑡) =
𝑠(𝑡)
4
𝑥̇( 𝑡) =
𝑠̇( 𝑡)
4
𝑥̈( 𝑡) =
𝑠̈( 𝑡)
4
EDM:
𝑚 𝑥̈ = (𝑇 − 𝑚𝑔)
𝑥( 𝑡) =
𝑠(𝑡)
4
𝑥̇( 𝑡) =
𝑠̇( 𝑡)
4
𝑥̈( 𝑡) =
𝑠̈( 𝑡)
4
• Desmultiplicação
de Forças
• Desmultiplicação
de Forças

9. 9
Princípio Base: 𝑥 𝑚𝑜𝑙𝑎( 𝑡) =
𝑠(𝑡) 𝑚𝑜𝑣𝑒𝑙
2
𝑇 = −𝐾𝑒𝑞 𝑥(𝑡)
Análise Válida quando numa roldana móvel há diminuição do comprimento de um lado (fixo) e aumento do
comprimento da corda no outro (móvel)

10. 10
1- Sistemas c/ 1 Grau Liberdade
1.1- Introdução
• Teoremas Vetoriais da Dinâmica (TVD): ∑ 𝐹 = ∑ 𝑄⃗̇
𝑖𝑗
∑ 𝑀 𝑂 = ∑ 𝐾 𝑂
⃗⃗⃗⃗⃗𝑖𝑗
• Teorema dos Trabalhos Virtuais (TTV): 𝑊𝑒𝑥𝑡 + 𝑊𝑣𝑖𝑟𝑡𝑢𝑎𝑙 + 𝑊𝑗 = 0
• Equação Diferencial do Movimento (EDM):
1 G.L Linear ( ∑ 𝑚𝑖𝑖 ) 𝑥̈ ( ∑ 𝑐𝑓𝑓 ) 𝑥̇ + (∑ 𝑘𝑗𝑗 + ∑
𝑚 𝑖 𝑔
𝑙𝑖 ) 𝑥 = 𝑘𝑠( 𝑡) + 𝑐𝑠̇( 𝑡)
1 G.L Angular ( ∑ 𝑚𝑖𝑖 𝑙2 ) 𝜃̈ + ( ∑ 𝑐𝑓𝑓 𝑙2 ) 𝜃̇ + ( ∑ 𝑘𝑗𝑗 𝑙2
+ ∑ 𝑚𝑖𝑖 𝑔𝑙 ) 𝜃 = 𝑙 ⋅ 𝑘𝑠( 𝑡) + 𝑙 ⋅ 𝑐𝑠̇( 𝑡) + 𝐹𝑙 ⋅
𝑐𝑜𝑠( 𝜔𝑡)
[𝑁𝑠2
/𝑚] [𝑁𝑠/𝑚] [𝑁/𝑚] + [𝑁]
𝑘𝑔 𝑐 𝑘 𝑚𝑔
[𝐾𝑔] =
[𝑁𝑠2
/𝑚]
[𝑔] =
[𝑚/𝑠2]
1 G.L Torsional ( ∑ 𝐽𝑖𝑖 ) 𝜃̈ + ( ∑ 𝑐𝑡 𝑓𝑓 ) 𝜃̇ + ( ∑ 𝑘𝑡 𝑗𝑗 ) 𝜃 = 𝑀 ⋅ 𝑐𝑜𝑠( 𝜔𝑡)
[𝑁𝑠2
𝑚] [𝑁𝑠 𝑚] [𝑁𝑚]
𝑘𝑔 𝑚2
𝑐𝑡 𝑘𝑡
Propriedades de Vibração do Sistema :
• Frequência Natural não amortecida: 𝜔 𝑛 = √
𝑘 𝑒𝑞
𝑚 𝑒𝑞
; 𝑇𝑛 =
2𝜋
𝜔 𝑛
• Frequencia Natural amortecida: 𝜔 𝑑 = 𝜔 𝑛√1 − 𝜉2 ; 𝑇𝑑 =
2𝜋
𝜔 𝑑
• Razão de Amortecimento: 𝜉 =
𝑐 𝑒𝑞
2 𝑚 𝑒𝑞 ⋅ 𝜔 𝑛
• Constante de Amortecimento Crítico: 𝑐 𝑐 = 2 𝑚 𝑒𝑞 ⋅ 𝜔 𝑛
• Obtenção Experimental da Rigidez Equivalente: 𝑘 𝑒𝑞 = 𝑓𝑒𝑠𝑡 ⋅
1
𝑑 𝑒𝑠𝑡
Excitação (velocidade)
Imposta ao Amortecedor
Deslocamento
Imposto à
Mola

11. 11
1.2- Regime Livre (Equação Diferencial Ordinária Linear Homogênea)
• Equação Diferencial do Movimento Base:
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [𝑐 𝑒𝑞] 𝑥̇ + [𝑘 𝑒𝑞] 𝑥 = 0
1.2.1- Sistema Subamortecido , 𝟎 ≤ 𝝃 < 𝟏
• Resposta do Sistema
𝑥( 𝑡) = 𝐴𝑒− 𝜉𝜔 𝑛 𝑡
cos( 𝜔 𝑑 𝑡 − 𝜑) 𝜔 𝑑 = 𝜔 𝑛√1 − 𝜉2
𝑥̇( 𝑡) = −𝐴 ⋅ 𝜔 𝑛 ⋅ 𝑒− 𝜉𝜔 𝑛 𝑡
cos( 𝜔 𝑑 𝑡 − 𝜑 − 𝜓) , 𝐴 = √(
𝑥̇ 𝑜+𝜉𝜔 𝑛 𝑥 𝑜
𝜔 𝑑
)
2
+ 𝑥 𝑜
2
𝜑 = tan−1
(
1
𝑥 𝑜
⋅
𝑥̇ 𝑜+𝜉𝜔 𝑛 𝑥 𝑜
𝜔 𝑑
)
𝜓 = tan−1
(
√1−𝜉2
𝜉
)
• Equações das Envelopes – dependem apenas do amortecimento
𝑦 = 𝐴𝑒−𝜉𝜔 𝑛 𝑡
• Determinação Experimental de ( 𝜉) – Metodo do Decremento Logarítmico (δ) para 0 < 𝜉 < 1
𝛿 =
1
𝑁
ln (
𝑥(𝑡1)
𝑥(𝑡1+𝑁⋅𝑇 𝑑)
) , N=1, 2, 3,.. (nº de ciclos entre as duas medições)
𝜉 =
𝛿
√ 4𝜋2+𝛿2
• Respostas Máxima 𝑥( 𝑡) | 𝑚𝑎𝑥 e Instante em que ocorre 𝑡| 𝑥 𝑚𝑎𝑥
ou Energia Poencial Maxima:
𝑡| 𝑥 𝑚𝑎𝑥
=
1
𝜔 𝑑
(tan−1( 𝐸) + 𝜑) 𝐸 = −
𝜉
√1−𝜉2
𝑥( 𝑡) | 𝑚𝑎𝑥 = 𝐴𝑒 𝐸 [tan−1(𝐸)+𝜑]
cos(tan−1
(𝐸)) (or just plug in the 𝑡| 𝑥 𝑚𝑎𝑥
in the response
expression )
• Overshoot
• Velocidade Máxima ou 1ª vez que o sistema passa pela Posição de Equilibrio Estático

12. 12
1.2.2- Resposta do Sistema Criticamente Amortecido , 𝝃 = 𝟏
𝑥( 𝑡) = [ 𝑥̇ 𝑜 + 𝑥0 𝜔 𝑛] 𝑒− 𝜔 𝑛 𝑡
[ 𝑡 +
𝑥 𝑜
𝑥̇ 𝑜+𝑥0 𝜔 𝑛
]
𝑥̇( 𝑡) = [ 𝑥̇ 𝑜 + 𝑥0 𝜔 𝑛] ⋅ 𝜔 𝑛 ⋅ 𝑒− 𝜔 𝑛 𝑡
[
1
𝜔 𝑛
− 𝑡 −
𝑥 𝑜
𝑥̇ 𝑜+𝑥0 𝜔 𝑛
]
1.2.3- Resposta do Sistema Sobreamortecido , 𝝃 > 𝟏
𝑥( 𝑡) = 𝑒− 𝜉𝜔 𝑛 𝑡
[ A1 cosh(𝜔 𝑛√𝜉2 − 1 𝑡) +A2 sinh(𝜔 𝑛√𝜉2 − 1 𝑡) ] A1 = 𝑥 𝑜
𝑥̇( 𝑡) =
𝑑
𝑑𝑡
[𝑥( 𝑡)] A2 =
𝑥̇ 𝑜+𝜉𝜔 𝑛 𝑥 𝑜
𝜔 𝑛√𝜉2−1

13. 13
1.3- Regime Forçado Periódico - Harmônico (E.D.L.O.N.)
1.4.1- Solicitação Harmónica Ativa - Força Discreta
• Equação Diferencial do Movimento Base:
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [𝑐 𝑒𝑞] 𝑥̇ + [𝑘 𝑒𝑞] 𝑥 = 𝐹𝑒𝑞cos(𝜔𝑡)
ou
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [𝑐 𝑒𝑞] 𝑥̇ + [𝑘 𝑒𝑞] 𝑥 = 𝐹𝑒𝑞sin(𝜔𝑡)
• Resposta Permanente do Sistema
𝑥 𝑝( 𝑡) = 𝑋( 𝜔) ⋅ cos(𝜔𝑡 − 𝜑)
𝑥 𝑝( 𝑡) = 𝑋( 𝜔) ⋅ sin(𝜔𝑡 − 𝜑)
𝑋(𝜔) = 𝑋𝑠 ⋅ 𝜇
𝜑 = tan−1
(
2𝜉𝛽
1−𝛽2
)
𝑋𝑠 =
𝐹𝑒𝑞
𝑘 𝑒𝑞
𝜇 =
1
√(1−𝛽2)2+(2𝜉𝛽)2
;
𝛽 =
𝜔
𝜔 𝑛
• Valores Críticos – Válidos para 𝜉 ≤
√2
2
𝛽| 𝜇 𝑚𝑎𝑥
= √1 − 2𝜉2
𝜇 𝑚𝑎𝑥 =
1
2𝜉√1−𝜉2
𝜔𝑟 = 𝜔 𝑛 √1 − 2𝜉2
𝑋 𝑚𝑎𝑥 = 𝑋𝑠 ⋅ 𝜇 𝑚𝑎𝑥
𝛽| 𝜇=1 = √2 − 4𝜉2
Objetivo (Sistema):
Diminuição da amplitude da resposta de
modo a diminuir:
- os problemas de desgaste e fadiga do
componente mecânico
- precisão dimensional
Solução (sem alterar resposta estática – μ ):
- 𝜔 ↑ (Ex: aumentar velocidade avião)
- 𝜉 ↑ ⇔ 𝑐 ↑
Origem Forças Harmônicas:
- Forças devido à ação das
ondas em plataformas
marítimas
- Forças em prensas
hidráulicas
- Forças de arrasto em asas
de aviões
Nota: 𝜇| 𝜉=0
=
1
|1−𝛽2|
Análise válida para Sistemas Não
Amortecidos ou Sub-amortecidos

14. 14
Objetivo (Apoios):
- Isolamento de fontes de vibração
(equipamentos rotativos)
- Durabilidade dos apoios de fontes de
vibração (fundações de plataformas
marítimas, uniões das asas dos aviões à
fuselagem)
-
• Transmissibilidade de Força
𝑇𝑅 =
𝐹𝑇
𝐹
razão entre a amplitude da força transmitida (𝐹 𝑇) e a
amplitude da força de solicitação ( ≠ 𝐹𝑒𝑞 )
𝑓𝑇(𝑡) = __𝑘𝑥( 𝑡) + __𝑐𝑥̇( 𝑡) = 𝐹 𝑇 cos( 𝜔𝑡 − 𝜑 + 𝛾)
𝐹 𝑇 = √(__𝑘)2 + (__𝑐𝜔)2 ⋅ 𝑋( 𝜔) =
= √(__𝑘)2 + (__𝑐𝜔)2 ⋅
𝐹 𝑒𝑞
𝐾 𝑒𝑞
⋅ 𝜇
Nota: Sempre que num apoio esteja inserido um amortecedor, a Transmissibilidade de força TR é
deteriorada pela força de amortecimento a partir de certos valores de 𝛽 ( 𝐹𝑐 = 𝑐𝑥̇( 𝑡) )
𝑇𝑅 =
√(__𝑘)2+(__𝑐𝜔)2 𝑋(𝜔)
𝐹
=
𝐹 𝑒𝑞
𝐹
⋅
√(__𝑘)2+(__𝑐𝜔)2
𝐾 𝑒𝑞
⋅ 𝜇
Diminuição da Transmissibilidade de Força:
- 𝜔 𝑛 ↓
- 𝜉 𝑚𝑖𝑛 para evitar picos elevados na transição pela frequência de ressonância
(contudo com efeito prejudicial para 𝛽 ≥ √2 )
Redução da Transmissibilidade/vibrações ou Eficiência do Isolamento ( R ):
𝑇𝑅 = 1 − 𝑅

15. 15
1.4.2 - Solicitação Harmónica Ativa – Rotação de Massas em Desiquilibrio
• Resposta Permanente do Sistema
𝑥 𝑝( 𝑡) = 𝑋(𝜔) ⋅ sin(𝜔𝑡 − 𝜑)
𝑋(𝜔) = 𝑋𝑠 ⋅ 𝜇 𝑟𝑜𝑡
𝜑 = tan−1
(
2𝜉𝛽
1−𝛽2
)
𝑋𝑠 =
𝑒 𝑚 𝑜
𝑚 𝑒𝑞
;
𝜇 𝑟𝑜𝑡 =
𝛽2
√(1−𝛽2)2+(2𝜉𝛽)2
𝛽 =
𝜔
𝜔 𝑛
• Valores Críticos – Válido para 𝜉 ≤
√2
2
𝛽| 𝜇 𝑚𝑎𝑥
=
1
√1−2𝜉2
𝜇 𝑚𝑎𝑥 =
1
2𝜉√1−𝜉2
(o valor do pico efetivo não se altera,
apenas muda a sua posição)
𝜔 𝑟 =
𝜔 𝑛
√1−2𝜉2
𝑋 𝑚𝑎𝑥 = 𝑋𝑠 ⋅ 𝜇 𝑚𝑎𝑥
Curiosidade: 𝜇 𝑟𝑜𝑡 = 𝜇 ⋅
𝑚 𝑒𝑞 𝜔2
𝑘 𝑒𝑞
𝑓𝑒( 𝑡) = 𝑒 𝑚 𝑜 𝜔2
sin(𝜔𝑡)
𝐹𝑒𝑞 = 𝑒 𝑚 𝑜 𝜔2
Nota: 𝜇 𝑟𝑜𝑡 | 𝜉=0
=
𝛽2
|1−𝛽2|

16. 16
1.4.3- Solicitação Harmónica Passiva
• Equação Diferencial do Movimento
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [𝑐 𝑒𝑞] 𝑥̇ + [𝑘 𝑒𝑞] 𝑥 = 𝑘𝑦 + 𝑐𝑦̇
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [𝑐 𝑒𝑞] 𝑥̇ + [𝑘 𝑒𝑞] 𝑥 = √𝑘2 + ( 𝑐𝜔)2 𝑦(𝑡 + 𝛾)
• Resposta Permanente do Sistema
𝑥 𝑝( 𝑡) = 𝑋( 𝜔) ⋅ cos( 𝜔𝑡 + 𝛾 − 𝜑 )
𝑥 𝑝( 𝑡) = 𝑋( 𝜔) ⋅ sin( 𝜔𝑡 + 𝛾 − 𝜑 )
𝑋(𝜔) = 𝑋𝑠 ⋅ 𝜇
𝜑 = tan−1
(
2𝜉𝛽
1−𝛽2
)
𝛾 = tan−1( 2𝜉𝛽 )
𝑋𝑠 =
𝐹𝑒𝑞
𝑘 𝑒𝑞
; 𝐹𝑒𝑞 = 𝑌√( __𝑘)2 + ( __ 𝑐𝜔)2
𝜇 =
1
√(1−𝛽2)2+(2𝜉𝛽)2
Nota: √( 𝑓( 𝑥) )2 = | 𝑓( 𝑥) |
𝛽 =
𝜔
𝜔 𝑛
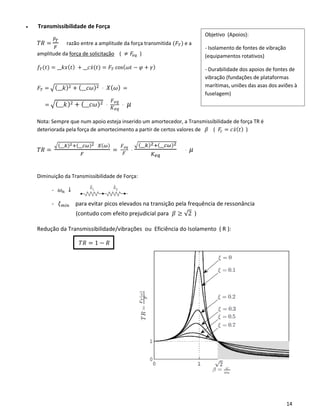
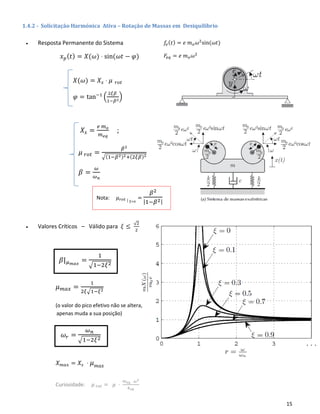
• Transmissibilidade de Deslocamento:
𝑇𝑅𝑓𝑜𝑟𝑐𝑎 =
𝐹 𝑇
𝑌
=
𝐹𝑒𝑞
𝑌 𝐾 𝑒𝑞
⋅ 𝜇 =
𝑇𝑅 𝑎𝑏𝑠 =
𝑋(𝜔)
𝑌
=
𝐹𝑒𝑞
𝑌 𝐾 𝑒𝑞
⋅ 𝜇 =
=
√( __𝑘)2+( __ 𝜔𝑐)2
𝑘 𝑒𝑞
⋅ 𝜇
Origem dos Deslocamentos
Harmónicos Impostos:
- Vibrações devido à atividade
sísmica
- Vibração de veiculos devido a
imperfeiçoes do terreno
- Vibrações das bases/apoios
devido a outros sistemas
𝑦( 𝑡) = 𝑌 cos(𝜔𝑡)
𝑦( 𝑡) = 𝑌 sin(𝜔𝑡)
Zona de
Isolamento

17. 17
Zona
de
1.4.4- Isolamento de Vibrações
Técnicas de Isolamento de Vibrações (Considerando ξ =0 para simplificação):
• Bloco de Isolamento
𝑚 𝑒𝑞 ↑↑
Apenas adequado para sistemas ligeiros - para que a massa dos apoios nao seja desprezável (Ex:
Aparelhagem de medição...)
Ex: Mesas de Aparelhagem laboratorial, Prensas e Máquinas Ferramenta
pesadas
𝑅 = 1 − 𝑇𝑅 ⇒ 𝜔 𝑛
2
= 𝜔 2 1−𝑅
2−𝑅
⇒ 𝑚 𝑒𝑞 =
𝑘
𝜔2
2−𝑅
1−𝑅
• Plataforma de Isolamento
𝑘 ↓↓
Adequado para sistemas de elevado atravancamento (Ex: pontes,
automóveis...)
Deflecção Estática do próprio sistema 𝑋𝑆 ↑↑ (arranque)
Ex: Placas Elastoméricas, bases de moals helicoidais, bases de ar
comprimido (apresenta algum amortecimento natural)
𝑅 = 1 − 𝑇𝑅 ⇒ 𝜔 𝑛
2
= 𝜔 2 1−𝑅
2−𝑅
⇒ 𝑘 𝑒𝑞 = 𝑚 𝜔2 1−𝑅
2−𝑅
Equivalência da Transmissibilidade de Força ( 𝑇𝑅 ) e Transmissibilidade de deslocamento absoluto ( 𝑇𝑅 𝑎𝑏𝑠 ) :
𝑇𝑅𝑓𝑜𝑟ç𝑎 =
𝐹 𝑇
𝐹
=
𝑘 𝑚𝑜𝑙𝑎 𝑋(𝜔)
𝐹
=
𝑘 𝑚𝑜𝑙𝑎 𝐹𝑒𝑞
𝐹 𝑘 𝑒𝑞
𝜇 = 𝜇 =
1
|1−𝛽2|
=
1
𝛽2−1
=
1
𝜔2
𝜔 𝑛
2−1
𝑇𝑅 𝑎𝑏𝑠 =
𝑋(𝜔)
𝑌
=
𝐹𝑒𝑞
𝑌 𝑘 𝑒𝑞
𝜇 =
𝑘 𝑌
𝑌 𝑘 𝑒𝑞
𝜇 = 𝜇 =
1
|1−𝛽2|
=
1
𝛽2−1
𝑅 = 1 − 𝑇𝑅 = 1 −
1
𝜔 2
𝜔 𝑛
2−1
⇔
𝜔 2
𝜔 𝑛
2 − 1 =
1
1−𝑅
⇔
𝜔 2
𝜔 𝑛
2 =
2−𝑅
1−𝑅
⇔ 𝜔 𝑛
2
= 𝜔 2 1−𝑅
2−𝑅

18. 18
Conceitos Derivados EXCLUSIVAMENTE para o
sistema representado
Aceleração Teórica do
Sistema
𝑦( 𝑡) = 𝑌 sin(𝜔𝑡)
𝑦̈( 𝑡) = −𝑌𝜔2
sin(𝜔𝑡)
1.4.5- Transdutor de Vibrações
Estudo do Transdutor Sísmico
• O transdutor Sísmico apenas regista o movimento
relativo 𝑧(𝑡) (entre a régua graduada da caixa, e o
apontador da massa)
• Equação Diferencial de Movimento
[ 𝑚 ] 𝑥̈ + [ 𝑐] 𝑥̇ + [ 𝑘] 𝑥 = 𝑘𝑦 + 𝑐𝑦̇
𝑚𝑥̈ + 𝑐𝑥̇ − 𝑐𝑦̇ + 𝑘𝑥 − 𝑘𝑦 = 0 ; 𝑧(𝑡) =
𝑥(𝑥) − 𝑦(𝑡)
𝑚 𝑧̈ + 𝑐 𝑧̇ + 𝑘𝑧 = −𝑚𝑦̈ = 𝑚𝜔2
𝑦 , 𝐹𝑒𝑞 = 𝑌𝑚𝜔2
𝑧( 𝑡) = 𝑍( 𝜔) sin( 𝜔𝑡 − 𝜑) ; 𝑍( 𝜔) =
𝐹𝑒𝑞
𝑘
𝜇 =
𝑌𝑚𝜔2
𝑘
𝜇 = 𝑌𝜇 𝑟𝑜𝑡
Dimensionamento de Vibrómetros - Transmissibilidade Relativa
𝑇𝑅 𝑟𝑒𝑙 =
𝑍(𝜔)
𝑌
=
𝑌 𝜇 𝑟𝑜𝑡
𝑌
= 𝜇 𝑟𝑜𝑡
Para que 𝑍( 𝜔) = 𝑌(𝜔)
é necessário que 𝑇𝑅 𝑟𝑒𝑙 = 𝜇 𝑟𝑜𝑡
= 1
Erro Medição (E): 𝐸 = |1 – 𝑇𝑅 𝑟𝑒𝑙|
Dimensionamento de Acelerámetro
Manipulação da Resposta Relativa 𝑧(𝑡)
𝑧( 𝑡) =
𝐹𝑒𝑞
𝑘
𝜇 sin( 𝜔𝑡) =
𝑌𝑚𝜔2
𝑘
𝜇 sin( 𝜔𝑡 − 𝜑)
−𝑧( 𝑡) = −
𝑌𝑚𝜔2
𝑘
𝜇 sin( 𝜔𝑡 − 𝜑)
−𝑧( 𝑡)
𝑘
𝑚
= − 𝜇 𝑌𝜔2
sin( 𝜔𝑡 − 𝜑) ⇔
−𝑧( 𝑡) 𝜔 𝑛
2
= − 𝜇 𝑌𝜔2
sin( 𝜔𝑡 − 𝜑)
◊ É necessário que 𝜇 = 1
◊ Basta medir o deslocamento 𝑧(𝑡) e afeta-lo da constante −𝜔 𝑛
2
e
obtem-se facilmente a aceleração do sistema
Erro Medição (E): 𝐸 = |1 – 𝜇|

19. 19
1.4- Regime Forçado Periódico - Não Harmônico
• Equação Diferencial do Movimento Base:
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [𝑐 𝑒𝑞] 𝑥̇ + [𝑘 𝑒𝑞] 𝑥 = 𝑓( 𝑡)
• Modelação da Excitação ( Expansão de 𝑓(𝑡) pela serie de Fourier: )
𝑓( 𝑡) =
𝐹0
2
+ ∑ 𝐹𝑝cos(𝑝𝜔𝑡 − 𝛾𝑝)∞
𝑝=1 expressão ja agrupada
𝐹0 = 𝑣𝑎𝑙𝑜𝑟 𝑚é𝑑𝑖𝑜 =
2
𝑇
∫ 𝑓( 𝑡) 𝑑𝑡
𝑇
0
𝐹𝑝 = √𝐴 𝑝
2
+ 𝐵𝑝
2
𝛾𝑝 = tan−1
(
𝐵 𝑝
𝐴 𝑝
)
𝐴 𝑝 =
2
𝑇
∫ 𝑓( 𝑡)∗
⋅ cos( 𝑝𝜔𝑡) 𝑑𝑡
𝑇
0
em que 𝜔 =
2𝜋
𝑇
𝐵𝑝 =
2
𝑇
∫ 𝑓( 𝑡)∗
⋅ sin( 𝑝𝜔𝑡) 𝑑𝑡
𝑇
0
T – periodo da solicitação periódica
• Resposta Permanente do Sistema
𝑥 𝑝( 𝑡) =
𝐹0
2𝐾𝑒𝑞
+ ∑ 𝑋 𝑝(𝜔) ⋅ cos(𝑝𝜔𝑡 − 𝜑 𝑝 − 𝛾𝑝)∞
𝑝=1
𝑋 𝑝(𝑝𝜔) = 𝑋𝑠𝑝 𝜇 𝑝 𝑋𝑠𝑝 =
𝐹𝑝
𝑘 𝑒𝑞
𝜇 𝑝 =
1
√(1−𝛽 𝑝)
2
−(2𝜉𝛽 𝑝)
2
𝛽 𝑝 = 𝑝𝜔/𝜔 𝑛
• Critério de Truncatura da Série:
Paridade de 𝑓( 𝑡)
/ par impar
𝐴 𝑝 - 0
𝐵𝑝 0 -
𝛾𝑝
0
𝑘
= 0
0
−𝑘
= 𝜋
𝑘
0
=
𝜋
2
−𝑘
0
= −
𝜋
2
Relação 𝝎 𝒓 ∞ 𝝎 Truncatura (p)
𝜔 ≪ 𝜔𝑟 ∈ [1, 𝑝 =
𝜔𝑟
𝜔
+ 𝜀]
𝜔 ≈ 𝜔𝑟 ou 𝜔 ≫ 𝜔𝑟 ∈ [1, 1 + 𝜀]
Resolução na máquina (não é CaseSensitie):
𝐴 𝑝 =
2
𝑎
∫ 𝑓( 𝑡) ⋅ cos (𝑝
2𝑟
𝑎
𝑡) 𝑑𝑡
𝑎
0
𝐵𝑝 =
2
𝑎
∫ 𝑓( 𝑡) ⋅ sin (𝑝
2𝑟
𝑎
𝑡) 𝑑𝑡
𝑎
0

20. 20
1.5- Regime Forçado Não Periódico (Impulsiva e transiente)
1.7.1- Regime Forçado Impulsivo
• Equação Diferencial do Movimento Base:
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [𝑐 𝑒𝑞] 𝑥̇ + [𝑘 𝑒𝑞] 𝑥 = 𝑓( 𝑡) = 𝐹̃ 𝛿( 𝑡 − 𝜏)
Teorema do Impulso e Q.M: 𝐹̌ = ∫ 𝑓( 𝑡) 𝑑𝑡
𝑡+𝛥𝑡
𝑡
= 𝛥𝑄 = 𝑚𝛥𝑥̇
Função Impulso Unitário: 1 = ∫ 𝛿(𝑡 − 𝜏)𝑑𝑡
+∞
−∞
Definição alternativa de força impulsiva: 𝑓( 𝑡) = 𝐹̌ 𝛿(𝑡 − 𝜏)
Função Resposta Impulsiva: ℎ( 𝑡 − 𝜏) =
1
𝑚𝜔 𝑑
𝑒−𝜉𝜔 𝑛 (𝑡−𝜏)
sin [𝜔 𝑑 ( 𝑡 − 𝜏)]
• Resposta total a uma força impulsiva - 𝑥(𝑡)
𝑥( 𝑡) = {
𝐴𝑒−𝜉𝜔 𝑛 𝑡
𝑐𝑜𝑠(𝜔 𝑑 𝑡 − 𝜑), 𝑡 > 0
𝐹̃
𝑚𝜔 𝑑
𝑒−𝜉𝜔 𝑛 (𝑡−𝜏)
sin [ 𝜔 𝑑 ( 𝑡 − 𝜏̅)] , 𝑡 ≥ 𝜏̅
𝜏̅ − 𝑖𝑛𝑠𝑡𝑎𝑛𝑡𝑒 𝑑𝑒 𝑎𝑡𝑢𝑎çã𝑜 𝑑𝑜 𝑖𝑚𝑝𝑢𝑙𝑠𝑜 (𝑣𝑎𝑙𝑜𝑟 𝑓𝑖𝑛𝑖𝑡𝑜, 𝑛ã𝑜 é 𝑣𝑎𝑟𝑖á𝑣𝑒𝑙!)
1.7.2- Regime Forçado Transiente
• Equação Diferencial do Movimento Base:
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [𝑐 𝑒𝑞] 𝑥̇ + [𝑘 𝑒𝑞] 𝑥 = 𝑓( 𝑡) = ∫ 𝑓( 𝜏) 𝑑𝜏
𝑡 𝑐
0
• Modelação da Excitação
Modelação do sinal
de excitação tendo o zero
como origem do referencial
(referência τ inicial). No final afetar f (τ
– τ) e introduzir a informação de
desfasamento na atuação de f nos
limites de integração
Análise válida para Sistemas:
• Não Amortecidos
• Sub-amortecidos

21. 21
• Resposta total do sistema
𝑥( 𝑡) =
{
𝐴𝑒−𝜉𝜔 𝑛 𝑡 𝑐𝑜𝑠( 𝜔 𝑑 𝑡 − 𝜑) , 𝑡 > 0
1
𝑚 𝑒𝑞 𝜔 𝑑
⋅ [ ∫ f(τ − 𝜏) ⋅ e−𝜉𝜔 𝑛 (𝑡−𝜏)
⋅ sin[ 𝜔 𝑑( 𝑡 − 𝜏)] 𝑑𝜏
𝑡
𝜏
] , 𝜏̅ < 𝑡 < 𝑡 𝑐
1
𝑚 𝑒𝑞 𝜔 𝑑
⋅ [ ∫ f(τ − 𝜏) ⋅ e−𝜉𝜔 𝑛 (𝑡−𝜏)
⋅ sin[ 𝜔 𝑑( 𝑡 − 𝜏)] 𝑑𝜏
𝑡 𝑐
𝜏
] , 𝑡 > 𝑡 𝑐
Em que: 𝜏 − instante de aplicação da força impulsiva transiente
𝜏 − variável tempo que descreve a atuação da força impulsiva,variável de integração
𝑡 − variável tempo que descreve de forma geral a resposta do sistema,associada precisamente
à resposta do sistema,nunca é integrada
𝑡 𝑐 − intanste em que finda a aplicação da força transiente

22. 22
2 - Graus de Liberdade
2.1 – Introdução
• Formalismo ou Procedimento de Lagrange – Baseado no principio Variacional de Hamilton
𝑑
𝑑𝑡
(
𝜕
𝜕𝑞̇ 𝑖
L) +
𝜕
𝜕𝑞̇ 𝑖
F −
𝜕
𝜕𝑞𝑖
L = Q i ou
𝑑
𝑑𝑡
(
𝜕
𝜕𝑞̇ 𝑖
T) +
𝜕
𝜕𝑞̇ 𝑖
F −
𝜕
𝜕𝑞𝑖
T +
𝜕
𝜕𝑞𝑖
V = Q i
em que: 𝐿 = 𝑇 – 𝑉 e Q i =
𝜕
𝜕𝑞 𝑖
(𝑊𝐹) representa as forças generalizadas nao conservativas
• Função Dissipativa de Rayleigh
𝐹 =
1
2
∑ [ 𝑐 ( 𝑣2 − 𝑣1)2 ]
𝑛
𝑗
• Medição Experimental da Rigidez:
𝑓𝑖 = 𝑘𝑖𝑗 𝑑𝑗 , 𝑑𝑖 = 𝛼𝑖𝑗 𝑓𝑗 [𝑘] = [𝑎]−1
(𝑚𝑎𝑡𝑟𝑖𝑧 𝑑𝑒 𝑓𝑙𝑒𝑥𝑖𝑏𝑖𝑙𝑖𝑑𝑎𝑑𝑒)
• Equação Diferencial do Movimento Básica
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [ 𝑐 𝑒𝑞 ] 𝑥̇ + [ 𝑘 𝑒𝑞 ] 𝑥 = 0
• Definir os Modos Naturais de Vibração (Assumindo sistema não amortecido)
| 𝑥|1 = | 𝑢|1 cos(𝜔1 𝑡 − 𝜑1)
| 𝑥|2 = | 𝑢|2 cos(𝜔2 𝑡 − 𝜑2)
• Frequencias Naturais ( Resolução Analítica )
𝑑𝑒𝑡( −𝜔2[𝑚] + [𝑘] ) = 0 ⇒
𝑠𝑜𝑙𝑣𝑒( 𝜔4[ 𝑚11 𝑚22 − 𝑚12
2 ] − 𝜔2[ 𝑚11 𝑘22 + 𝑚22 𝑘11 − 2𝑚12 𝑘12 ] + [ 𝑘11 𝑘22 − 𝑘12
2] = 0)
• Frequência Fundamental (Quociente de Rayleigh – Resuloção Aproximada)
𝑅(| 𝑣|) =
| 𝑣| 𝑇 [𝑘] | 𝑣|
| 𝑣| 𝑇 [𝑚] | 𝑣|
em que | 𝑣| = [𝐾]−1
⋅ 𝑑𝑖𝑎𝑔[𝑚]
𝑅(| 𝑣|) ≅ 𝜔1
2
⇒ 𝜔1 ≅ √𝑅(| 𝑣|)
• Vetor Modal
| 𝑢1| = |
1
𝑟1
| ; | 𝑢2| = |
1
𝑟2
| ;
𝑟1 = −
𝜔1
2 𝑚12−𝑘12
𝜔1
2 𝑚22−𝑘22
; 𝑟2 = −
𝜔2
2 𝑚12−𝑘12
𝜔2
2 𝑚22−𝑘22
𝑑
𝑑𝜃
𝑠𝑖𝑛𝜃 = cos(𝜃)
𝑑
𝑑𝜃
cos( 𝜃) = −sin(𝜃)
𝑑
𝑑𝑡
𝑠𝑖𝑛𝜃 = 𝜃̇cos(𝜃)
𝑑
𝑑𝜃
cos( 𝜃) = −𝜃̇sin(𝜃)

23. 23
• Vetor Modal Normalizado - Normalização dos vetores modais para massas modas unitárias
|𝜑 𝑖| =
1
√|𝑢𝑖| 𝑇[𝑚]|𝑢𝑖|
|𝑢1| ⇒ |𝜑 𝑖| =
1
√𝑚22 𝑟𝑖
2+2𝑚12 𝑟𝑖+𝑚11
|
1
𝑟𝑖
|
Na MAQ texas nspire: |𝜑 𝑖| =
1
√det( | 𝑢𝑖| 𝑇[𝑚]|𝑢𝑖| )
|𝑢1|
• Matriz Modal Normalizada
[𝛷] = [ | 𝜑1| | 𝜑2| ]
• Transformação para Coordendas Naturais ou Coordenadas Modais
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [ 𝑐 𝑒𝑞 ] 𝑥̇ + [ 𝑘 𝑒𝑞 ] 𝑥 = |𝐹|
[ 𝑚 𝑒𝑞 ] [𝜑] | 𝑛̈| + [ 𝑐 𝑒𝑞 ] [𝜑] | 𝑛̇| + [ 𝑘 𝑒𝑞 ] [𝜑] | 𝑛| = | 𝐹|
| 𝑛̈| + [ 𝛺 ] | 𝑛| = [𝛷] 𝑇 | 𝐹| em que [ 𝛺2 ] = [
𝜔1
2
0
0 𝜔2
2]
2.2 – Regime Livre ( Sistemas Não Amortecidos)
• Equação Diferencial do Movimento Básica
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [ 𝑘 𝑒𝑞 ] 𝑥 = 0
• Resposta Livre ou Transitória– Combinação Linear dos Modos Naturais de Vibração excitados
| 𝑥( 𝑡) | = [ 𝑈 ] |
𝑐1cos(𝜔1 𝑡 − 𝜑1)
𝑐2cos(𝜔2 𝑡 − 𝜑2)
| , em que [ 𝑈 ] = ⌈
1 1
𝑟1 𝑟2
⌉
𝑐1 =
1
𝑟2−𝑟1
√( 𝑟2 𝑥1
0
− 𝑥2
0)2 +
(𝑟2 𝑥̇1
0−𝑥̇2
0)
2
𝜔1
2
𝑐1 =
1
𝑟2−𝑟1
√( 𝑟1 𝑥1
0
− 𝑥2
0)2 +
(𝑟1 𝑥̇1
0−𝑥̇2
0)
2
𝜔2
2
tan( 𝜑1) =
𝑟2 𝑥̇1
0−𝑥̇2
0
𝜔1(𝑟2 𝑥1
0−𝑥2
0)
atenção ao caso de tan(𝜑1) = 0 ( 0+
ou 0-
?? )
tan( 𝜑2) =
𝑟1 𝑥̇1
0−𝑥̇2
0
𝜔2(𝑟1 𝑥1
0−𝑥2
0)

24. 24
Sistema Secundário
ou auxiliar
Sistema Primário
ou Principal
2.3- Regime Forçado Harmônico
2.3.1 – Introdução
• Equação Diferencial do Movimento Básica
[ 𝑚 𝑒𝑞 ] | 𝑥̈ | + [ 𝑘 𝑒𝑞 ] | 𝑥 | = | 𝐹| 𝑒 𝑗𝜔𝑡
( −𝜔2[ 𝑚 𝑒𝑞 ] + [ 𝑘 𝑒𝑞 ] ) | 𝑋( 𝜔)| = | 𝐹|
• Resposta Permanente
| 𝑥(𝑡)| = |
𝑋̅1(𝜔)
𝑋̅2(𝜔)
| cos( 𝜔𝑡)
|
𝑋̅1( 𝜔)
𝑋̅2( 𝜔)
| = [ 𝑍 ]−1 | 𝐹| seja [ 𝑧 ] = −𝜔2[ 𝑚 ] + [𝑘]
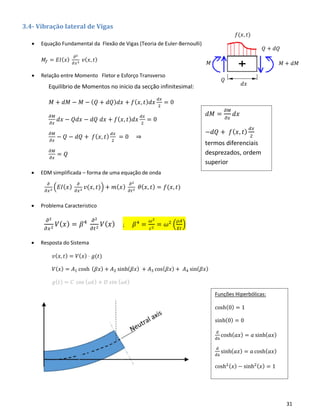
2.4.2 – Absorsor de Vibrações
• Aumento da Gama de funcionamento do
Absorsor
o 𝜺 ↑ ⇒ 𝑚2 ↑ , pouco conveniente
o Introdução de amortecimento
(contudo a resposta nunca será nula
!!!)
• Parâmetros dos Sistemas Isolados
o Parâmetros adicionais de dimensionamento:
𝛼 =
𝜔 𝑛 𝑠
𝜔 𝑛 𝑝
𝛽 =
𝜔
𝜔 𝑛 𝑝
𝜀 =
𝑚2
𝑚1
𝜔 𝑛 𝑝
= √
𝑘1
𝑚1
𝜔 𝑛 𝑠
= √
𝑘2
𝑚2
o Condição de Absorção de Vibrações:
𝜔 𝑛 𝑠 = 𝜔 = √
𝑘2
𝑚2
(1)
Nota de Dimensionamento:
- Dimensionamento com base em
parâmetros dos sitemas isolados
- Dualidade na nomencaltura dos
vários parâmetros (propriedades dos
sistemas isolados, propriedades dos
sitema Global)
Equivalência da modelação das solicitações:
𝑓( 𝑡) = 𝐹𝑐𝑜𝑠(𝜔𝑡) | 𝑥( 𝑡)| = | 𝑋̅(𝜔)|cos(𝜔𝑡)
Ou ⇒
𝑓( 𝑡) = 𝐹𝑠𝑖𝑛(𝜔𝑡) | 𝑥( 𝑡)| = | 𝑋̅(𝜔)|sin(𝜔𝑡)

25. 25
Equivalência da modelação das solicitações:
𝑓( 𝑡) = 𝐹𝑐𝑜𝑠(𝜔𝑡) | 𝑥( 𝑡)| = | 𝑋̅( 𝜔) |cos(𝜔𝑡)
Ou ⇒
𝑓( 𝑡) = 𝐹𝑠𝑖𝑛(𝜔𝑡) | 𝑥( 𝑡)| = | 𝑋̅( 𝜔) |sin(𝜔𝑡)
• Parâmetros do Sistema Global
o Resposta Forçada dos dois corpos (Absorsor Sintonizado)
𝑋̅1 ≈ 0
𝑋̅2 = −
𝐹𝑒𝑞
𝑘1
⋅
1
𝜀𝛽2
cos(𝜔𝑡)
𝑋̅2 = −
𝐹𝑒𝑞
𝑘2
o Frequências Naturais ( Situação Genérica de 𝜔 𝑛 𝑠 ≠ 𝜔 , absorsor não sintonizado )
(1 − 𝛽2)( 𝛼2
− 𝛽2) − 𝜀𝛼4
𝛽2
= 0 Eq. Característica baseada nos parâmetros isolados
𝜔1
2
=
(𝜔 𝑛 𝑝)
2
2
[ (1 + 𝛼2
+ 𝛼2
𝜀) − √(1 + 𝛼2 + 𝛼2 𝜀)2 − 4𝛼2 ] usar expressão no critério ii)
𝜔2
2
=
(𝜔 𝑛 𝑝)
2
2
[ (1 + 𝛼2
+ 𝛼2
𝜀) + √(1 + 𝛼2 + 𝛼2 𝜀)2 − 4𝛼2 ]
( 𝑘1 + 𝑘2 − 𝜔1
2
𝑚1)( 𝑘2 − 𝜔1
2
𝑚2) = 0 (usar sistema no critério iii)
( 𝑘1 + 𝑘2 − 𝜔2
2
𝑚1)( 𝑘2 − 𝜔2
2
𝑚2) = 0

26. 26
• Dimensionamento do Absorsor/Secundário
i) Critério – sintonização do absorsor + relação de massas fixa (projeto)
{
𝑘2 = 𝜔2
𝑚2
𝑚2 = 𝜀 ⋅ 𝑚1
ii) Critério – sintonização do absorsor + limite para a amplitude de funcionamento
{
𝑘2 = 𝜔2
𝑚2
𝜔1 ≤ 𝐶𝑡𝑒
ou {
𝑘2 = 𝜔2
𝑚2
𝜔2 ≥ 𝐶𝑡𝑒
iii) Critério – largura da amplitude de funcionamento (absorsor não
sintonizado !!!)
{
𝜔1 ≤ 𝐶 𝑡𝑒
𝜔2 ≥ 𝐶 𝑡𝑒
iv) Critério – sintonização do absorsor + amplitude de resposta do
secundário máxima
{
𝑘2 = 𝜔2
𝑚2
𝑋̅2 = −
𝐹 𝑒𝑞
𝑘2

27. 27
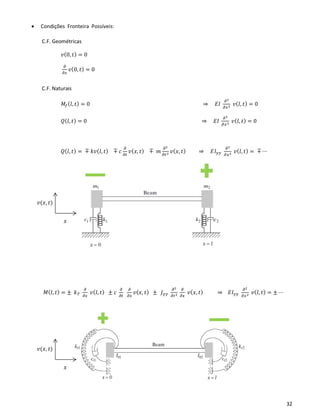
2.5 – Regime Forçado Transiente
• Procedimento da Análise Modal:
1º) Calcular o vetor solicitação nas Coordenadas Naturais
2º) Calcular a resposta nas coordenadas modais ou naturais (Pelas técnicas aplicadas a sistemas com 1 G.L.,
isto porque trata-se de um sistema de ED desacoplado)
3º) Determinar a resposta nas coordenadas generalizadas pelo conceito de matriz de transformação
• EDM nas Coordenadas Naturais
[𝐼]| 𝑛̈( 𝑡) | + [𝛺2] | 𝑛( 𝑡) | = [𝛷] 𝑇 | 𝑓(𝑡)| = | 𝑁| em que [𝛺2] = [
𝜔1
2
0
0 𝜔2
2] e [𝐼] = [
1 0
0 1
]
{
𝑛1̈ ( 𝑡) + 𝜔1
2
𝑛1( 𝑡) = 𝜑11 𝑓1( 𝑡) + 𝜑21 𝑓2( 𝑡) = 𝑁1
𝑛2̈ ( 𝑡) + 𝜔2
2
𝑛2( 𝑡) = 𝜑12 𝑓1( 𝑡) + 𝜑22 𝑓2( 𝑡) = 𝑁2
• Vetor Solicitação nas Cordenadas Naturais
|
𝑁1(𝑡)
𝑁2(𝑡)
| = [
𝜑11 𝜑12
𝜑21 𝜑22
]
𝑇
|
𝑓1(𝑡)
𝑓2(𝑡)
|
• Resposta nas Coordenadas Generalizadas :
|
𝑥1(𝑡)
𝑥2(𝑡)
| = [
𝜑11 𝜑12
𝜑21 𝜑22
] |
𝑛1(𝑡)
𝑛2(𝑡)
|
• Resposta Natural ao Transiente Degrau / Degrau unitário ( 𝝃 = 𝟎 ) :
𝜂𝑖( 𝑡) =
𝑁 𝑖
𝜔𝑖
2 [ 1 − cos( 𝜔𝑖 𝑡) ]
• Resposta Natural ao Transiente Rectangular ( 𝝃 = 𝟎 ) :
𝜂𝑖( 𝑡) =
• Resposta Natural a meia onda sin ( 𝝃 = 𝟎 ) :
𝜂𝑖( 𝑡) =
𝑁 𝑖
𝜔1
2
[ 1 − cos( 𝜔𝑖 𝑡) ] para 𝑡 ≤ 𝑡 𝑐
𝑁 𝑖
𝜔 𝑖
2
[ cos[ 𝜔𝑖( 𝑡 − 𝑡 𝑐) ] − cos( 𝜔𝑖 𝑡) ] para 𝑡 > 𝑡 𝑐
𝑁 𝑖
𝜔1
2
𝜔𝑖⋅𝑡 𝑐
[ (𝜔𝑖⋅𝑡 𝑐)2−𝜋2]
⋅ [ 𝜔𝑖 𝑡 𝑐 sin(
𝜋
𝑡 𝑐
⋅ 𝑡) − 𝜋sin( 𝜔𝑖 𝑡) ] para 𝑡 ≤ 𝑡 𝑐
𝑁 𝑖
𝜔𝑖
2
𝜔 𝑖 𝜋 tc
[ 𝜋2− (𝜔𝑖⋅𝑡 𝑐)2]
[ sin[ 𝜔𝑖( 𝑡 − 𝑡 𝑐)] + sin( 𝜔𝑖 𝑡) ] para 𝑡 > 𝑡 𝑐

28. 28
3- Sistemas Contínuos
3.1- Vibração Lateral de Cordas
• EDM simplificada – forma de uma equação de onda
𝜕
𝜕𝑥
(
𝜕
𝜕𝑥
𝑇( 𝑥) 𝑣(𝑥, 𝑡)) = 𝑚(𝑥)
𝜕2
𝜕𝑡2 𝑣( 𝑥, 𝑡)
𝜕2
𝜕𝑥2 𝑉( 𝑥) =
1
𝐶2
𝜕2
𝜕𝑡2 𝑉( 𝑥) , 𝐶2
=
𝑇
𝜇
• Problema Característico
𝜕
𝜕𝑥
(𝑇( 𝑥)
𝜕
𝜕𝑥
𝑉(𝑥)) + 𝜔2
𝑚( 𝑥) 𝑉(𝑥) = 0
• Resposta do Sistema
𝑣( 𝑥, 𝑡) = 𝑉( 𝑥) ⋅ 𝑔(𝑡)
𝑉( 𝑥) = 𝐴 cos (
𝜔
𝑐
𝑥) + 𝐵 𝑠𝑖𝑛 (
𝜔
𝑐
𝑥)
𝑔( 𝑡) = 𝐶 cos ( 𝜔𝑡) + 𝐷 𝑠𝑖𝑛 ( 𝜔𝑡)
• Confições Fronteira Possíveis
Exemplos de String vibration Behaviour:
- Vibração induzido por escoamento (flow induced
vibration) devido às forças de arrasto e elevação (Drag
and Lift Forces ) provocada pelos vortices de distruição
da camada limite,
- Em: cabos de aço e veios cilíndricos longos em
Plataformas petrolíferas, boias sinalizadoras, tubos
subaquáticos, tirantes ,etc
- Elementos Mecânicos sem capacidade de absorção
de momentos
C.F. Geométricas
𝑣(0, 𝑡) = 0 apoio duplo/encastramento
C.F. Naturais
𝑇
𝜕
𝜕𝑥
𝑣( 𝑙, 𝑡) = 0
𝑇
𝜕
𝜕𝑥
𝑣( 𝑙, 𝑡) = ± 𝑘𝑣( 𝑙, 𝑡) ± 𝑐
𝜕
𝜕𝑡
𝑣( 𝑙, 𝑡) ± 𝑚
𝜕2
𝜕𝑡2 𝑣(𝑙, 𝑡)
𝑥
𝑣(𝑥, 𝑡)

29. 29
3.2- Vibração Longitudinal de Barras
• Equação da Elasticidade de Barras
𝑃( 𝑥, 𝑡) = 𝐴𝐸( 𝑥)
𝜕
𝜕𝑥
𝑢(𝑥, 𝑡)
• EDM simplificada – forma de uma equação de onda
𝜕
𝜕𝑥
(𝐸𝐴( 𝑥)
𝜕
𝜕𝑥
𝑢( 𝑥, 𝑡)) + 𝑓( 𝑥, 𝑡) = 𝑚(𝑥)
𝜕2
𝜕𝑡2 𝑈( 𝑥)
𝜕2
𝜕𝑥2 𝑢( 𝑥, 𝑡) =
1
𝐶2
𝜕2
𝜕𝑡2 𝑢( 𝑥, 𝑡) , 𝐶2
=
𝐸
𝜌
• Problema Característico
𝜕
𝜕𝑥
(𝐸𝐴( 𝑥)
𝜕
𝜕𝑥
𝑈(𝑥)) + 𝜔2
𝑚( 𝑥) 𝑈(𝑥) = 0
• Resposta do Sistema
𝑢( 𝑥, 𝑡) = 𝑈( 𝑥) ⋅ 𝑔(𝑡)
𝑈( 𝑥) = 𝐴 cos (
𝜔
𝑐
𝑥) + 𝐵 𝑠𝑖𝑛 (
𝜔
𝑐
𝑥)
𝑔( 𝑡) = 𝐶 cos ( 𝜔𝑡) + 𝐷 𝑠𝑖𝑛 ( 𝜔𝑡)
• Condições Fronteira Possíveis:
Exemplos de Vibração Longitudinal:
- Vibração nas ferramentas de percursão de
martelos pneumáticos
- Vibração em serrotes industriais (introduzida
pelos dentes)
- Toda a acústica e seus problemas (som é uma
onda mecânica de propagação longitudinal.
Notar apenas que nenhuma onda
eletromagnética propaga-se longitudinalmente,
apenas transversalmente)
C.F. Geométricas
𝑢(0, 𝑡) = 0
C.F. Naturais
𝑃( 𝑙, 𝑡) = 0 ⇒ 𝐸𝐴
𝜕
𝜕𝑥
𝑢( 𝑙, 𝑡) = 0
𝑃( 𝑙, 𝑡) = ±𝑘𝑢( 𝑙, 𝑡) ± 𝑐
𝜕
𝜕𝑡
𝑢( 𝑙, 𝑡) ± 𝑚
𝜕2
𝜕𝑡2 𝑢( 𝑙, 𝑡) ⇒ 𝐸𝐴
𝜕
𝜕𝑥
𝑢( 𝑙, 𝑡) = ±⋯
𝑥
𝑢(𝑥, 𝑡)

30. 30
3.3- Vibração Torsional de Veios
• Equação Fundamental da Torção de Veios (Relação da Elasticidade)
𝑀 𝑇 = 𝐺 𝐼 𝑝( 𝑥)
𝜕
𝜕𝑥
𝜃(𝑥, 𝑡)
• Equação Diferencial do Movimento
𝜕
𝜕𝑥
(𝐺𝐼 𝑝( 𝑥)
𝜕
𝜕𝑥
𝜃(𝑥, 𝑡)) + 𝑓(𝑥, 𝑡) = 𝑚( 𝑥)
𝜕2
𝜕𝑡2 𝜃(𝑥, 𝑡)
• Problema Característico
𝜕
𝜕𝑥
(𝐺𝐼 𝑝( 𝑥)
𝜕
𝜕𝑥
𝛩(𝑥)) + 𝜔2
𝐽( 𝑥) 𝛩(𝑥) = 0
• Resposta do Sistema
𝑢( 𝑥, 𝑡) = 𝛩( 𝑥) ⋅ 𝑔(𝑡)
𝑈( 𝑥) = 𝐴 cos (
𝜔
𝑐
𝑥) + 𝐵 𝑠𝑖𝑛 (
𝜔
𝑐
𝑥)
𝑔( 𝑡) = 𝐶 cos ( 𝜔𝑡) + 𝐷 𝑠𝑖𝑛 ( 𝜔𝑡)
• Condições Fronteira Possíveis:
Nomenclatura
Geometria de Massas:
𝐽𝑣𝑒𝑖𝑜 = 𝐽( 𝑥) 𝑙
𝐽( 𝑥) = 𝜌 𝐼 𝑝
𝐽𝑣𝑒𝑖𝑜 = 𝜌 𝐼 𝑝 𝑙
C.F. Geométricas
𝜃(0, 𝑡) = 0
C.F. Naturais
𝑀𝑡( 𝑙, 𝑡) = 0 ⇒ 𝐺𝐼 𝑝
𝜕
𝜕𝑥
𝜃( 𝑙, 𝑡) = 0
𝑀𝑡( 𝑙, 𝑡) = ±𝑘𝜃( 𝑙, 𝑡) ± 𝑐
𝜕
𝜕𝑡
𝜃( 𝑙, 𝑡) ± 𝐽𝑣𝑜𝑙𝑎𝑛𝑡𝑒
𝜕2
𝜕𝑡2 𝑐 ⇒ 𝐺𝐼 𝑝
𝜕
𝜕𝑥
𝜃( 𝑙, 𝑡) = ± …
𝜃(𝑥, 𝑡)
𝑀𝑡(𝑥, 𝑡)

31. 31
𝑀 + 𝑑𝑀
𝑄 + 𝑑𝑄
𝑄
𝑀
𝑑𝑥
𝑓(𝑥, 𝑡)
3.4- Vibração lateral de Vigas
• Equação Fundamental da Flexão de Vigas (Teoria de Euler-Bernoulli)
𝑀𝑓 = 𝐸𝐼( 𝑥)
𝜕2
𝜕𝑥2 𝑣( 𝑥, 𝑡)
• Relação entre Momento Fletor e Esforço Transverso
• EDM simplificada – forma de uma equação de onda
𝜕
𝜕𝑥2 (𝐸𝐼( 𝑥)
𝜕
𝜕𝑥2 𝑣(𝑥, 𝑡)) + 𝑚( 𝑥)
𝜕2
𝜕𝑡2 𝜃( 𝑥, 𝑡) = 𝑓(𝑥, 𝑡)
• Problema Caracteristico
𝜕2
𝜕𝑥2
𝑉( 𝑥) = 𝛽4 𝜕2
𝜕𝑡2
𝑉( 𝑥) ; 𝛽4
=
𝜔2
𝑐2
= 𝜔2
(
𝜌𝐴
𝐸𝐼
)
• Resposta do Sistema
𝑣( 𝑥, 𝑡) = 𝑉( 𝑥) ⋅ 𝑔(𝑡)
𝑉( 𝑥) = 𝐴1 cosh ( 𝛽𝑥) + 𝐴2 sinh( 𝛽𝑥) + 𝐴3 cos( 𝛽𝑥) + 𝐴4 sin( 𝛽𝑥)
𝑔( 𝑡) = 𝐶 cos ( 𝜔𝑡) + 𝐷 𝑠𝑖𝑛 ( 𝜔𝑡)
Equilibrio de Momentos no inicio da secção infinitesimal:
𝑀 + 𝑑𝑀 − 𝑀 − ( 𝑄 + 𝑑𝑄) 𝑑𝑥 + 𝑓( 𝑥, 𝑡) 𝑑𝑥
𝑑𝑥
2
= 0
𝜕𝑀
𝜕𝑥
𝑑𝑥 − 𝑄𝑑𝑥 − 𝑑𝑄 𝑑𝑥 + 𝑓( 𝑥, 𝑡) 𝑑𝑥
𝑑𝑥
2
= 0
𝜕𝑀
𝜕𝑥
− 𝑄 − 𝑑𝑄 + 𝑓( 𝑥, 𝑡)
𝑑𝑥
2
= 0 ⇒
𝜕𝑀
𝜕𝑥
= 𝑄
𝑑𝑀 =
𝜕𝑀
𝜕𝑥
𝑑𝑥
−𝑑𝑄 + 𝑓( 𝑥, 𝑡)
𝑑𝑥
2
termos diferenciais
desprezados, ordem
superior
Funções Hiperbólicas:
cosh(0) = 1
sinh(0) = 0
d
dx
cosh( 𝑎𝑥) = 𝑎 sinh( 𝑎𝑥)
d
dx
sinh( 𝑎𝑥) = 𝑎 cosh( 𝑎𝑥)
cosh2( 𝑥) − sinh2( 𝑥) = 1

32. 32
• Condições Fronteira Possíveis:
C.F. Geométricas
𝑣(0, 𝑡) = 0
𝜕
𝜕𝑥
𝑣(0, 𝑡) = 0
C.F. Naturais
𝑀𝑓( 𝑙, 𝑡) = 0 ⇒ 𝐸𝐼
𝜕2
𝜕𝑥2 𝑣( 𝑙, 𝑡) = 0
𝑄( 𝑙, 𝑡) = 0 ⇒ 𝐸𝐼
𝜕3
𝜕𝑥3 𝑣( 𝑙, 𝑡) = 0
𝑄( 𝑙, 𝑡) = ∓ 𝑘𝑣( 𝑙, 𝑡) ∓ 𝑐
𝜕
𝜕𝑡
𝑣( 𝑥, 𝑡) ∓ 𝑚
𝜕2
𝜕𝑡2 𝑣( 𝑥, 𝑡) ⇒ 𝐸𝐼 𝑦𝑦
𝜕3
𝜕𝑥3 𝑣( 𝑙, 𝑡) = ∓ ⋯
𝑀( 𝑙, 𝑡) = ± 𝑘 𝑇
𝜕
𝜕𝑥
𝑣( 𝑙, 𝑡) ± 𝑐
𝜕
𝜕𝑡
𝜕
𝜕𝑥
𝑣( 𝑥, 𝑡) ± 𝐽 𝑦𝑦
𝜕2
𝜕𝑡2
𝜕
𝜕𝑥
𝑣( 𝑥, 𝑡) ⇒ 𝐸𝐼 𝑦𝑦
𝜕2
𝜕𝑥2 𝑣( 𝑙, 𝑡) = ± ⋯
𝑥
𝑣(𝑥, 𝑡)
𝑥
𝑣(𝑥, 𝑡)

33. 33
3.5- Metodo Aproximado da Energia de Rayleigh
3.5.1 – Procedimento
• Arbitar uma Função Admissível:
o Função admissível para problemas de 2ª ordem (deformação axial de barras, torção de veios)
𝛷( 𝑥) = 𝑎𝑥 + 𝑏
o Função admissível para problemas de 4ª ordem (flexão de vigas)
𝛹( 𝑥) = 𝑎𝑥2
+ 𝑏𝑥 + 𝑐
• Respeito pelas Condições Fronteira Geométricas
o Problemas de 2ª ordem (deformação axial de barras, torção de veios)
𝛷( 𝑙) = 0 ⇒ 𝑎(𝑙) + 𝑏 = 0
o Problemas de 4ª ordem (flexão de vigas)
𝛹( 𝑙) = 0 ⇒ 𝑎(𝑙)2
+ 𝑏(𝑙) + 𝑐
𝜕
𝜕𝑥
𝛹( 𝑙) = 0 ⇒ 2𝑎(𝑙) + 𝑏 = 0
• ( Adequabilidade da Função de aproximação do ponto de vista Físico )
– Traçar o gráfico da função aproximação e visualisar se esse movimento é
compatível com as condições fronteira, e se não é movimento de corpo rígido
(nenhum ponto com deslocamento nulo)
• Calcular o quociente de Rayleigh
o 𝜔 𝑅
2
=
𝑉 𝑚𝑎𝑥
𝑇∗
• Optimizar os parâmetros da função de aproximação
o
𝜕
𝜕𝛿
( 𝜔 𝑅
2) = 0 , procurar a função que introduz menor rigidez possível
Energia cinética de Referência
(sem a dependência do tempo)

34. 34
Elemento Linear
Energia Barra Veio Viga
𝑉𝑚𝑎𝑥
1
2
∫ 𝐴𝐸 [
𝜕
𝜕𝑥
𝛷( 𝑥)]
2
𝑑𝑥
𝑙
0
+ 𝑉𝑐𝑓𝑛
1
2
∫ 𝐺𝐼 𝑝 [
𝜕
𝜕𝑥
𝛷( 𝑥)]
2
𝑑𝑥
𝑙
0
+ 𝑉𝑐𝑓𝑛
1
2
∫ 𝐸𝐼 [
𝜕2
𝜕𝑥2
𝛷( 𝑥)]
2
𝑑𝑥
𝑙
0
+ 𝑉𝑐𝑓𝑛
𝑉𝑐𝑓𝑛 𝑉𝑐𝑓𝑛 =
𝑘
2
[ 𝛷( 𝑥)|𝑥= ]
2
𝑉𝑐𝑓𝑛 =
𝑘 𝑇
2
[ 𝛷( 𝑥)|𝑥= ]
2
𝑉𝑐𝑓𝑛 =
𝑘
2
[ 𝛷( 𝑥)|𝑥=]
2
+
𝑘 𝑇
2
[
𝜕
𝜕𝑥
𝛷( 𝑥)|𝑥=]
2
𝑇∗
1
2
∫ 𝜌𝐴 [ 𝛷( 𝑥)]2
𝑑𝑥
𝑙
0
+ 𝑇𝑐𝑓𝑛
1
2
∫ 𝜌𝐼 𝑝 [ 𝛷( 𝑥)]2
𝑑𝑥
𝑙
0
+ 𝑇𝑐𝑓𝑛
1
2
∫ 𝜌𝐴 [ 𝛷( 𝑥)]2
𝑑𝑥
𝑙
0
+ 𝑇𝑐𝑓𝑛
𝑇𝑐𝑓𝑛 𝑚 𝑝𝑒𝑠𝑜[ 𝛷( 𝑥)|𝑥= ]
2
𝐽 𝑣𝑜𝑙𝑎𝑛𝑡𝑒 [ 𝛷( 𝑥)|𝑥= ]
2
𝑚 𝑝𝑒𝑠𝑜[ 𝛷( 𝑥)|𝑥= ]
2
+
𝐼 𝑦𝑦 𝑖𝑛é𝑟𝑐𝑖𝑎
2
[
𝜕
𝜕𝑥
𝛷( 𝑥)|𝑥= ]
2

35. 35
3.6 – Considerações Práticas – Casos Particulares
3.6.1- Resolução Analítica do Problema Característico
• Variação de Secção
- Criação de n funções de deslocamento: 𝑢1( 𝑥1, 𝑡) 𝑒 𝑢2( 𝑥2, 𝑡) com referenciais distintos
- EDM:
𝜕
𝜕𝑥
(𝑘(𝑥)
𝜕
𝜕𝑥
𝑢1(𝑥1, 𝑡)) =
𝜕2
𝜕𝑡2 𝑢1(𝑥1, 𝑡)
𝜕
𝜕𝑥
(𝑘(𝑥)
𝜕
𝜕𝑥
𝑢2(𝑥2, 𝑡)) =
𝜕2
𝜕𝑡2 𝑢2(𝑥2, 𝑡)
- Funcoes caracteristicas: 𝑢 𝑛( 𝑥, 𝑡) {
𝐴1 cos (
𝜔 𝑛
𝑐
𝑥) + 𝐵1 sin(
𝜔 𝑛
𝑐
𝑥) 𝑝𝑎𝑟𝑎 𝑥 <
𝑙
2
𝐴2 cos (
𝜔 𝑛
𝑐
𝑥2) + 𝐵2 sin(
𝜔 𝑛
𝑐
𝑥2) 𝑝𝑎𝑟𝑎 𝑥2 <
𝑙
2
- Condições Fronteira
Veios, barras:
𝑢1(0, 𝑡) =. .. (condição fronteira 𝑥 = 0 , 1x)
𝑢1 (
𝑙
2
, 𝑡) = 𝑢2(0, 𝑡) (igualdade de deslocamento)
𝜕
𝜕𝑥
(𝑘(𝑥)
𝜕
𝜕𝑥
𝑢1( 𝑥, 𝑡)|
𝑥=
𝑙
2
) =
𝜕
𝜕𝑥
(𝑘(𝑥)
𝜕
𝜕𝑥
𝑢2( 𝑥, 𝑡)| 𝑥2=0
) (igualdade de esforço interno)
𝑢2 (
𝑙
2
, 𝑡) = ⋯ (condição fronteira 𝑥 = 𝑙 , 1x)
Vigas:
𝑣1(0, 𝑡) =. .. 𝑣1(0, 𝑡) =. .. (condições fronteira 𝑥 = 0 , 2x)
𝑣1 (
𝑙
2
, 𝑡) = 𝑣2(0, 𝑡) (igualdade de deslocamento)
𝜕
𝜕𝑥
𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
=
𝜕
𝜕𝑥
𝑣2( 𝑥, 𝑡)| 𝑥2=0
(igualdade de rotações)
𝜕
𝜕𝑥
(𝐸𝐼
𝜕
𝜕𝑥2 𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
) =
𝜕
𝜕𝑥
(𝐸𝐼
𝜕
𝜕𝑥2 𝑣2( 𝑥, 𝑡)| 𝑥2=0
) (igualdade de esforço transverso)
𝐸𝐼
𝜕2
𝜕𝑥2 𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
= 𝐸𝐼
𝜕2
𝜕𝑥2 𝑣2( 𝑥, 𝑡)| 𝑥2=0
(igualdade de momento fletor)
𝑣2 (
𝑙
2
, 𝑡) = ⋯ 𝑣2 (
𝑙
2
, 𝑡) =. .. (condições fronteira 𝑥 = 𝑙 , 2x)

36. 36
• Condições Fronteira Naturais a meio vão
- Criação de 2 funções de deslocamento: 𝑢1( 𝑥, 𝑡) 𝑒 𝑢2( 𝑥, 𝑡) ambas com o mesmo referencial x
- EDM
𝜕
𝜕𝑥
(𝑘(𝑥)
𝜕
𝜕𝑥
𝑢1(𝑥, 𝑡)) =
𝜕2
𝜕𝑡2 𝑢1( 𝑥, 𝑡) ;
𝜕
𝜕𝑥
(𝑘(𝑥)
𝜕
𝜕𝑥
𝑢2(𝑥, 𝑡)) =
𝜕2
𝜕𝑡2 𝑢2(𝑥, 𝑡)
- Funcoes caracteristicas: 𝑢 𝑛( 𝑥, 𝑡) {
𝐴1 cos (
𝜔 𝑛
𝑐
𝑥) + 𝐵1 sin (
𝜔 𝑛
𝑐
𝑥) 𝑝𝑎𝑟𝑎 𝑥 <
𝑙
2
𝐴2 cos (
𝜔 𝑛
𝑐
𝑥) + 𝐵2 sin (
𝜔 𝑛
𝑐
𝑥) 𝑝𝑎𝑟𝑎 𝑥2 <
𝑙
2
- Condições Fronteira
Veios, barras:
𝑢1(0, 𝑡) =. .. (condição fronteira 𝑥 = 0 , 1x)
𝑢1 (
𝑙
2
, 𝑡) = 𝑢2(0, 𝑡) (igualdade de deslocamento)
𝜕
𝜕𝑥
(𝑘( 𝑥)
𝜕
𝜕𝑥
𝑢1( 𝑥, 𝑡) |
𝑥=
𝑙
2
) = +
𝜕
𝜕𝑥
(𝑘(𝑥)
𝜕
𝜕𝑥
𝑢2( 𝑥2, 𝑡) | 𝑥=0
) − 𝑘𝑢2(0, 𝑡) − . ..
𝑢2 (
𝑙
2
, 𝑡) = ⋯ (condição fronteira 𝑥 = 𝑙 , 1x)
Vigas:
𝑣1(0, 𝑡) =. .. 𝑣1(0, 𝑡) =. .. (condições fronteira 𝑥 = 0 , 2x)
𝑣1 (
𝑙
2
, 𝑡) = 𝑣2(0, 𝑡) (igualdade de deslocamento)
𝜕
𝜕𝑥
𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
=
𝜕
𝜕𝑥
𝑣2( 𝑥, 𝑡)| 𝑥2=0
(igualdade de rotações)
𝜕
𝜕𝑥
(𝐸𝐼
𝜕
𝜕𝑥2 𝑣1( 𝑥, 𝑡) |
𝑥=
𝑙
2
) = +
𝜕
𝜕𝑥
(𝐸𝐼
𝜕
𝜕𝑥2 𝑣2( 𝑥, 𝑡) | 𝑥2=0
) + 𝑘𝑣2(0, 𝑡)+. ..
𝐸𝐼
𝜕2
𝜕𝑥2 𝑣1( 𝑥, 𝑡) |
𝑥=
𝑙
2
= 𝐸𝐼
𝜕2
𝜕𝑥2 𝑣2( 𝑥, 𝑡) | 𝑥2=0
(igualdade de Momento Fletor)
𝑣2 (
𝑙
2
, 𝑡) =. .. 𝑣2 (
𝑙
2
, 𝑡) =. .. (condições fronteira 𝑥 = 𝑙 , 2x)

37. 37
Vigas:
𝑣1(0, 𝑡) =. .. 𝑣1(0, 𝑡) =. .. (condições fronteira 𝑥 = 0 , 2x)
𝑣1 (
𝑙
2
, 𝑡) = 𝑣2 (
𝑙
2
, 𝑡) (igualdade de deslocamento)
𝜕
𝜕𝑥
𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
=
𝜕
𝜕𝑥
𝑣2( 𝑥, 𝑡)| 𝑥2=0
(igualdade de rotações)
𝜕
𝜕𝑥
(𝐸𝐼
𝜕
𝜕𝑥2 𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
) =
𝜕
𝜕𝑥
(𝐸𝐼
𝜕
𝜕𝑥2 𝑣2( 𝑥, 𝑡)| 𝑥2=0
) (igualdade de esforço Transv.)
𝐸𝐼
𝜕2
𝜕𝑥2 𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
= +𝐸𝐼
𝜕2
𝜕𝑥2 𝑣2( 𝑥, 𝑡)| 𝑥2=0
− 𝑘𝑣2(0, 𝑡)−. …
𝑣2 (
𝑙
2
, 𝑡) =. .. 𝑣2 (
𝑙
2
, 𝑡) =. .. (condições fronteira 𝑥 = 𝑙 , 2x)

38. 38
• Condições Fronteira Geométricas a meio vão ( Vigas )
Vigas:
𝑣1(0, 𝑡) =. .. 𝑣1(0, 𝑡) =. .. (condições fronteira 𝑥 = 0 , 2x)
𝑣1 (
𝑙
2
, 𝑡) = 0
𝑣2(0, 𝑡) = 0
𝜕
𝜕𝑥
𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
=
𝜕
𝜕𝑥
𝑣2( 𝑥, 𝑡)| 𝑥2=0
(igualdade de rotações)
𝐸𝐼
𝜕2
𝜕𝑥2 𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
= 𝐸𝐼
𝜕2
𝜕𝑥2 𝑣2( 𝑥, 𝑡)| 𝑥2=0
(igualdade de Momento Fletor)
𝑣2 (
𝑙
2
, 𝑡) = ⋯ 𝑣2 (
𝑙
2
, 𝑡) =. .. (condições fronteira 𝑥 = 𝑙 , 2x)
Vigas:
𝑣1(0, 𝑡) =. .. 𝑣1(0, 𝑡) =. .. (condições fronteira 𝑥 = 0 , 2x)
𝑣1 (
𝑙
2
, 𝑡) = 𝑣2 (
𝑙
2
, 𝑡) (igualdade de deslocamento)
𝜕
𝜕𝑥
𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
= 0
𝜕
𝜕𝑥
𝑣2( 𝑥, 𝑡)| 𝑥2=0
= 0
𝜕
𝜕𝑥
(𝐸𝐼
𝜕
𝜕𝑥2 𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
) =
𝜕
𝜕𝑥
(𝐸𝐼
𝜕
𝜕𝑥2 𝑣2( 𝑥, 𝑡)| 𝑥2=0
) (igualdade de esforço Transv.)
𝑣2 (
𝑙
2
, 𝑡) = ⋯ 𝑣2 (
𝑙
2
, 𝑡) =. .. (condições fronteira 𝑥 = 𝑙 , 2x)

39. 39
3.6.2- Método de Rayleigh
• Variação de Secção
𝑉𝑚𝑎𝑥 =
1
2
∫ 𝐴1 𝐸1 [
𝜕
𝜕𝑥
𝛷( 𝑥)]
2
𝑑𝑥
𝑙1
0
+
1
2
∫ 𝐴2 𝐸2 [
𝜕
𝜕𝑥
𝛷( 𝑥)]
2
𝑑𝑥
𝑙2
𝑙1
+. . . +𝑉𝑐𝑓𝑛
𝑇∗
=
1
2
∫ 𝜌1 𝐴1 [ 𝛷( 𝑥)]2
𝑑𝑥
𝑙1
0
+
1
2
∫ 𝜌2 𝐴2 [ 𝛷( 𝑥)]2
𝑑𝑥
𝑙2
𝑙1
+. . . +𝑇𝑐𝑓𝑛
• Condições Fronteira a meio vão
- Função aproximação com significado físico na posição da C.F a meio vão
(deslocamento máximo para C.F. fixo-fixo; nodo de vibração para livre-
livre
- Calcular 𝑉𝑐𝑓𝑛 𝑒 𝑇𝑐𝑓𝑛 para a C.F a meio vão