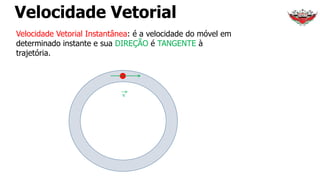
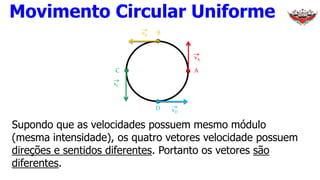
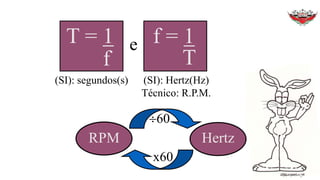
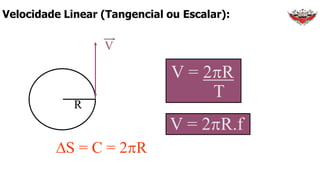
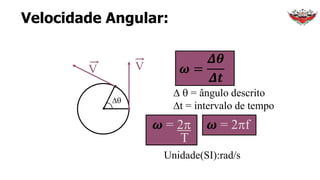
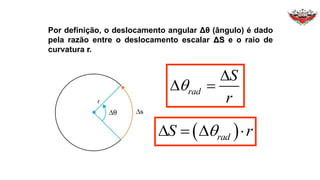
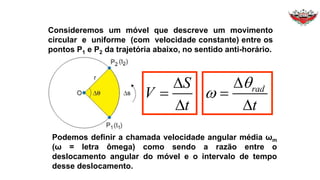
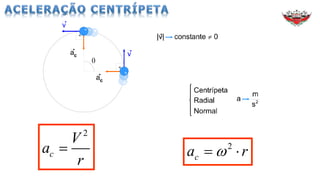
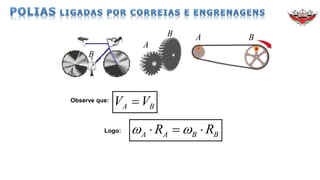
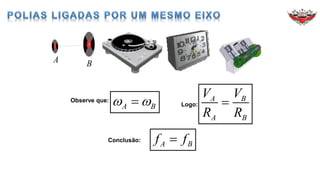
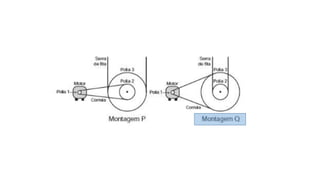
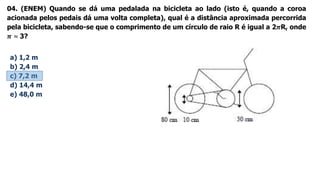
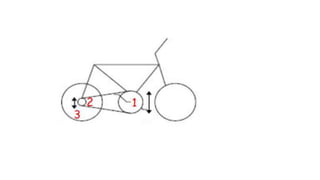
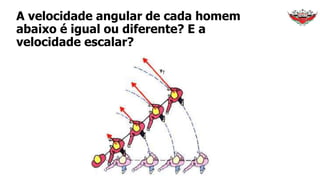
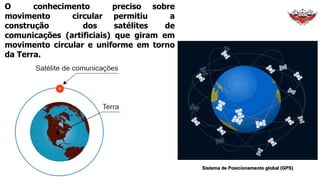
1) O documento discute conceitos sobre movimento circular uniforme, incluindo velocidade linear, angular e relações entre elas. 2) É apresentado que a velocidade angular é constante no movimento circular uniforme. 3) Exemplos como satélites e ponteiros de relógio ilustram o movimento circular uniforme.

1. e

2. O movimento circular está sempre presente em nossa vida, como no
movimento dos pneus de um automóvel que se desloca, no funcionamento
dos brinquedos giratórios de um parque de diversões, no movimento de
satélites ao redor da Terra, entre outros.
Movimento Circular Uniforme

3. Características: 1) Trajetória: curvilínea ou
circular.
2) Aceleração centrípeta:
constante em módulo e
diferente de zero.
3) Velocidade tangencial:
constante em módulo e
diferente de zero.
4) Aceleração tangencial: nula.
5) Vetor velocidade: variável,
pois muda constantemente a
direção e o sentido.

4. Velocidade Vetorial
Velocidade Vetorial Instantânea: é a velocidade do móvel em
determinado instante e sua DIREÇÃO é TANGENTE à
trajetória.
v

5. A
B
C
D
vA
vB
vC
vD
Supondo que as velocidades possuem mesmo módulo
(mesma intensidade), os quatro vetores velocidade possuem
direções e sentidos diferentes. Portanto os vetores são
diferentes.
Movimento Circular Uniforme

6. O conhecimento preciso sobre
movimento circular permitiu a
construção dos satélites de
comunicações (artificiais) que giram em
movimento circular e uniforme em torno
da Terra.
Sistema de Posicionamento global (GPS)

7. T = 1
f
f = 1
T
e
(SI): segundos(s) (SI): Hertz(Hz)
Técnico: R.P.M.
RPM Hertz
60
x60

8. Os ponteiros dos relógios
analógicos descrevem um
movimento circular e uniforme.
Nosso objetivo é estudar o movimento circular e
uniforme que, por definição, é um movimento em
que a velocidade escalar instantânea apresenta
intensidade constante.

9. Velocidade Linear (Tangencial ou Escalar):
.
R
V
V = 2R
T
V = 2R.f
DS = C = 2R

10. Velocidade Angular:
D  = ângulo descrito
Dt = intervalo de tempo
𝝎 = 2
T
𝝎 = 2f
Unidade(SI):rad/s
.
V
. D
.
V 𝝎 =
𝜟𝜽
𝜟𝒕

11. Por definição, o deslocamento angular Δθ (ângulo) é dado
pela razão entre o deslocamento escalar ΔS e o raio de
curvatura r.
rad
S
r

D
D 
 radS rD  D 

12. Consideremos um móvel que descreve um movimento
circular e uniforme (com velocidade constante) entre os
pontos P1 e P2 da trajetória abaixo, no sentido anti-horário.
S
V
t
D

D
D

D
rad
t


Podemos definir a chamada velocidade angular média ωm
(ω = letra ômega) como sendo a razão entre o
deslocamento angular do móvel e o intervalo de tempo
desse deslocamento.

13. No SI, a velocidade angular (ou pulsação) é dada em rad/s.
Em outros sistemas, pode ser uma unidade qualquer de
ângulo dividido por uma unidade de tempo.
Vamos relacionar as velocidades linear e angular:
S
V
t
D

D
rad
t


D

D
 radS rD  D 
 rad rS
V V
t t
D D
   
D D
V r 

14. 2
c
V
a
r
 2
ca r 

15. Observe que:
A
A
A
B
B B
A BV V
Logo:
A A B BR R   

16. Observe que:
A B
A B  Logo:
A B
A B
V V
R R

Conclusão:
A Bf f

17. A velocidade angular de cada homem
abaixo é igual ou diferente? E a
velocidade escalar?

18. 01. (ENEM) Um professor utiliza essa história em
quadrinhos para discutir com os estudantes o
movimento de satélites. Nesse sentido, pede a
eles que analisem o movimento do coelhinho,
considerando o módulo da velocidade constante.
Desprezando a existência de forças dissipativas, o
vetor aceleração tangencial do coelhinho, no
terceiro quadrinho, é
a) nulo.
b) paralelo à sua velocidade linear e no mesmo
sentido.
c) paralelo à sua velocidade linear e no sentido
oposto.
d) perpendicular à sua velocidade linear e dirigido
para o centro da Terra.
e) perpendicular à sua velocidade linear e dirigido
para fora da superfície da Terra.

19. 02. (ENEM) A invenção e o acoplamento entre engrenagens revolucionaram a
ciência na época e propiciaram a invenção de várias tecnologias, como os
relógios. Ao construir um pequeno cronômetro, um relojoeiro usa o sistema de
engrenagens mostrado. De acordo com a figura, um motor é ligado ao eixo e
movimenta as engrenagens fazendo o ponteiro girar. A frequência do motor é
de 18 RPM, e o número de dentes das engrenagens está apresentado no
quadro.
A frequência de giro do ponteiro, em RPM, é
a) 1. b) 2. c) 4. d) 81. e) 162.

20. 03. (ENEM) Para serrar os ossos e carnes congeladas, um açougueiro
utiliza uma serra de fita que possui três polias e um motor. O
equipamento pode ser montado de duas formas diferentes, P e Q. Por
questão de segurança, é necessário que a serra possua menor velocidade
linear.Por qual montagem o açougueiro deve optar e qual a justificativa
desta opção?
a) Q, pois as polias 1 e 3 giram com velocidades lineares iguais em
pontos periféricos e a que tiver maior raio terá menor frequência.
b) Q, pois as polias 1 e 3 giram com frequência iguais e a que tiver
maior raio terá menor velocidade linear em um ponto periférico.
c) P, pois as polias 2 e 3 giram com frequências diferentes e a que
tiver maior raio terá menor velocidade linear em um ponto
periférico.
d) P, pois as polias 1 e 2 giram com diferentes velocidades lineares
em pontos periféricos e a que tiver menor raio terá maior
frequência.
e) Q, pois as polias 2 e 3 giram com diferentes velocidades lineares
em pontos periféricos e a que tiver maior raio terá menor
frequência.

22. 04. (ENEM) Quando se dá uma pedalada na bicicleta ao lado (isto é, quando a coroa
acionada pelos pedais dá uma volta completa), qual é a distância aproximada percorrida
pela bicicleta, sabendo-se que o comprimento de um círculo de raio R é igual a 2𝝅R, onde
𝝅 ≈ 3?
a) 1,2 m
b) 2,4 m
c) 7,2 m
d) 14,4 m
e) 48,0 m