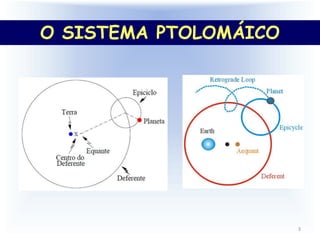
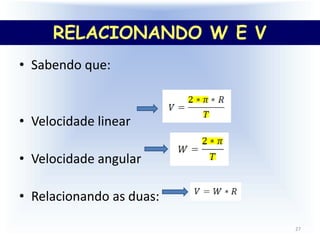
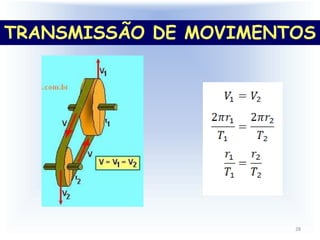
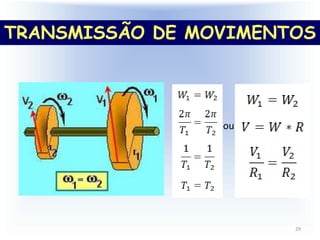
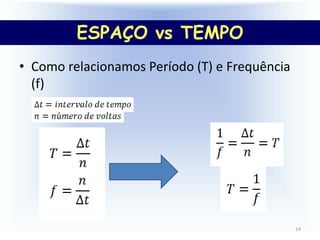
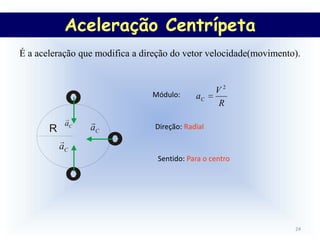
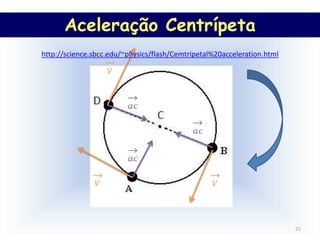
1) O documento discute o sistema Ptolemaico, que explicava o movimento dos planetas através de círculos concêntricos chamados de epiciclos e deferentes. 2) O sistema Ptolemaico descrevia a trajetória dos planetas como uma combinação de movimentos circulares em epiciclos e deferentes para explicar suas órbitas irregulares aparentes em torno da Terra. 3) O documento também aborda conceitos como período, frequência, velocidade angular, velocidade linear e aceleração centrípeta para explic

1. PONTIFÍCIA UNIVERSIDADE CATÓLICA DE SÃO PAULO
PROGRAMA SUPLEMENTAR FOCO VESTIBULAR
FÍSICA AULA 2
1

2. PTOLOMEU
2
• Geocentrismo: Explicou o movimento dos
planetas através de uma combinação de círculos.
• Epiciclo: pequeno ciclo ao redor do qual o planeta
se move.
• Deferente: o centro do epiciclo se move ao redor
desse círculo maior. O deferente é um círculo
excêntrico em relação a Terra.
• Equante: é um ponto ao lado do centro do
deferente oposto à posição da Terra, em relação
ao qual o centro do epiciclo se move.
PTOLOMEU

3. O Sistema Ptolomáico
3
O SISTEMA PTOLOMÁICO

4. O movimento dos planetas
• Qual é o formato da trajetória descrita?
• Qual é a distância que o planeta percorre?
• Em graus, é possível dizer quantas voltas um
planeta deu?
4
O MOVIMENTO DOS PLANETAS

5. • Pegue uma fita métrica e tire as medidas do
contorno (comprimento da circunferência) de
um objeto circular e de seu diâmetro.
• Divida o valor de seu comprimento pelo seu
diâmetro.
• Faça isso para mais de um objeto.
5
CIRCUNFERÊNCIA

6. • Exemplo:
• Comprimento: 27cm
• Diâmetro:8,5cm
• Resultados:
Esse número é
próximo a qual
número utilizado
na matemática?
6
CINCUNFERÊNCIA

7. • Chegamos a conclusão que:
Mas sabemos que:
Portanto:
7
CINCUNFERÊNCIA

8. 8
• Chegamos a conclusão que:
• Sabendo apenas o raio de uma circunferência
podemos descobrir o seu comprimento.
• No caso dos movimentos dos planetas o
comprimento da circunferência é a distância
percorrida durante uma volta.
• Uma volta também pode ser caracterizada
como 360 ou 2π radianos.
CINCUNFERÊNCIA

9. Espaço x Tempo
9
• 1 ano é o tempo que a Terra demora para dar
uma volta ao redor do Sol. (Translação)
• 24h é o tempo que a Terra demora para dar
uma volta ao redor dela mesma. (Rotação)
• Quanto tempo demora para o ponteiro dos
minutos dar uma volta completa no relógio?
• E o ponteiro das horas?
• E o ponteiro dos segundos?
ESPAÇO vs TEMPO

10. Espaço x Tempo
• Definimos PERíODO sendo o tempo para que
um corpo complete 1 volta.
• Através do simulador Solar System podemos
observar o período de alguns planetas.
• E se ao invés de nos perguntarmos:
• Em quanto tempo efetuamos 1 volta?
• Perguntarmos:
• Quantas voltas efetuamos em 1s ou em 1min?
10
ESPAÇO vs TEMPO

11. Espaço x Tempo
• Exemplo:
• Um corpo efetua 100 voltas em 20s.
a) Quanto tempo ele demora para dar uma
volta?
100 voltas 20s
1 volta X
100*X = 20
X=20/100
X=0,2s para efetuar 1 volta
11
ESPAÇO vs TEMPO

12. Espaço x Tempo
• Exemplo:
• Um corpo efetua 100 voltas em 20s.
b) Em 1s quantas voltas ele efetua?
100 voltas 20s
X 1s
20*X = 100
X=100/20
X=5 voltas efetuadas em 1s
12
ESPAÇO vs TEMPO

13. Espaço x Tempo
• Quando respondemos à questão (a) estamos
trabalhando com o período do movimento,
quando respondemos à questão (b) estamos
trabalhando com a frequência do movimento.
• Frequência é o número de repetições (no caso
do movimento circular as repetições são as
voltas) efetuadas por unidade de tempo.
13
ESPAÇO vs TEMPO

14. Espaço x Tempo
• Como relacionamos Período (T) e Frequência
(f)
14
ESPAÇO vs TEMPO

15. Espaço x Tempo: Velocidade
• O que é velocidade?
• Pode-se dizer que é a variação do espaço (∆S)
por unidade de tempo (∆t)?
• Seria:
15
ESPAÇO vs TEMPO
VELOCIDADE

16. Espaço x Tempo: Velocidade
• Velocidade linear (V) x Velocidade angular (W)
• O espaço no movimento circular
pode ser descrito pelo comprimento
da circunferência (2πR) ou pelo
ângulo varrido durante uma volta (2π).
16
ESPAÇO vs TEMPO
VELOCIDADE

17. Espaço x Tempo: Velocidade
• Considerando o comprimento da
circunferência, qual é o ∆S de uma volta?
• ∆S=2*π*R (velocidade linear)
• Qual o ∆t de uma volta?
• T=1/f
• Como podemos calcular a velocidade linear?
17
ESPAÇO vs TEMPO
VELOCIDADE

18. • Considerando o ângulo percorrido da
circunferência, qual é o ∆Φ de uma volta?
• ∆Φ =2*π (velocidade angular)
• Qual o ∆t de uma volta?
• T=1/f
• Como podemos calcular a velocidade angular?
18
ESPAÇO vs TEMPO
VELOCIDADE

19. Movimento Circular Uniforme
T
f
1
t
x
v
t
f
T
1
T
R
v
2 Rfv 2
T
2 f2
Rv
R
R
v
an
2
2
v
R
v
x
T: Período (Hz)
f: Freqüência (Hz)
v: Velocidade linear (m/s)
ω: Velocidade Angular (rad/s)
x: Comprimento do Arco (m)
ϴ: Ângulo (º)
t: Tempo (s)
R: Raio (m)
19

20. Freqüência (f): é o número de voltas na unidade de tempo
Unidades de f:
· rpm. (Rotações por Minuto)
· rps (Rotações por Segundo)
· rps = Ciclos/Segundo (1/s)= s -1 = Hz (hertz)
No SI: Hz
Exemplo:
Transforme : 120 rpm em Hz
Movimento Circular Uniforme
20

21. Movimento Circular Uniforme
t t
0
0t t0
t0
equação horária do movimento circular
uniforme
vtss 0 t
R
v
R
s
R
s 0
t0
R
v
21

22. Transmissão de Movimentos
Todos os pontos de um corpo rígido em rotação têm a mesma
velocidade angular.
Se ambos encontram-se na mesma engrenagem ou em uma mesma
correia não havendo escorregamento da correia ou do contato das
engrenagens.
Transmissão de Movimentos
22

23. Transmissão de Movimentos
Coroa maior que a catraca: maior velocidade à roda traseira resultando uma
maior velocidade da bicicleta.
Coroa menor que a catraca: maior força a roda traseira sendo usada para subir
uma ladeira.
Transmissão de Movimentos
23

24. É a aceleração que modifica a direção do vetor velocidade(movimento).
Módulo:
R
V
aC
2
Direção: Radial
Sentido: Para o centro
Ca
Ca
CaR
ACELERAÇÃO CENTRÍPETAAceleração Centrípeta
24

25. Aceleração Centrípeta
25
http://science.sbcc.edu/~physics/flash/Cemtripetal%20acceleration.html

26. Aceleração centrípeta
[m/s²]
Velocidade angular
[Rad/s]
Raio
[m]
Aceleração Centrípeta
26

27. 27
• Sabendo que:
• Velocidade linear
• Velocidade angular
• Relacionando as duas:
RELACIONANDO W E V

28. 28
TRANSMISSÃO DE MOVIMENTOS

29. 29
ou
TRANSMISSÃO DE MOVIMENTOS

30. 1) Duas polias, 1 e 2, são ligadas por uma correia. A polia 1 possui raio R1 , gira
com velocidade angular ω1, frequência f1 e período T1. A polia 2 possui raio R2,
gira com velocidade angular ω2, frequência f2 e período T2. Não há
escorregamento da correia sobre as polias. Sejam v1 e v2 as velocidades lineares
dos pontos P1 e P2.
Assinale a proposição correta:
I) v1 = v2
II) v1R1 = v2R2
III) ω1 = ω2
IV) ω1R1 = ω2R2
V) f1R1 = f2R2
VI) T1R1 = T2R2
Como não há escorregamento da correia
sobre as polias, concluímos que v1 = v2.
Sendo:
v1 = ω1.R1 e v2 = ω2.R2
ω1.R1 = ω2.R2
Sendo:
ω1 = 2π.f1 e ω2 = 2π.f2
Vem:
f1.R1 = f2.R2
Corretas: I); IV) e V)
Exercícios
30

31. As polias giram com a mesma velocidade angular e portanto com a mesma
frequência. Logo, apenas III é correta.
Assinale a proposição correta:
I) v1 = v2
II) v1R1=v2R2
III) ω1 = ω2
IV) ω1R1 = ω2R2
V) f1R1 = f2R2
VI) T1R1 = T2R2
2) Duas polias, 1 e 2, giram ligadas ao eixo de um motor. A polia 1 possui raio
R1, gira com velocidade angular ω1, frequência f1 e período T1. A polia 2 possui
raio R2, gira com velocidade angular ω2, frequência f2 e período T2. Sejam v1 e
v2 as velocidades lineares dos pontos P1 e P2.
Exercícios
31

32. 3) Determine a intensidade da aceleração centrípeta de um corpo que percorre
uma circunferência de raio 0,50 m com freqüência de 600rpm.
÷ 60
Ou
Ou
Exercícios
32

33. 33
EXERCÍCIO

34. 34
SIMULADOS
http://science.sbcc.edu/~physics/flash/LengthofDay.html