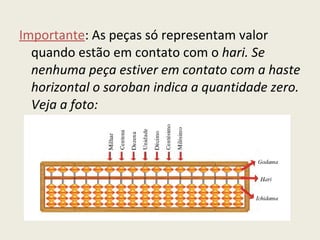
O documento fornece orientações gerais sobre os cadernos de matemática para professores, incluindo uma nova abordagem contextualizada dos conteúdos e ênfase nas competências pessoais como leitura e escrita matemática. As unidades estão organizadas em situações de aprendizagem e o documento fornece exemplos e recursos para professores.