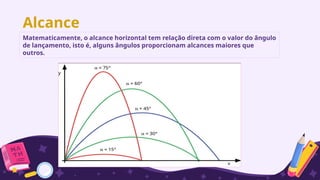
O documento aborda os conceitos de lançamento horizontal e oblíquo de um corpo, explicando as fórmulas relevantes para calcular o alcance, tempo de queda e componentes de velocidade. Inclui exemplos e problemas práticos que ilustram a aplicação das equações de movimento uniformemente variado (MUV) e o efeito do ângulo de lançamento no alcance horizontal. O texto busca esclarecer os princípios físicos por trás desses movimentos, enfatizando a importância das condições iniciais e das forças atuantes.

1. Lançament
o
Horizontal
Profº: Gean Costa

2. Introdução
Quando um corpo é lançado horizontalmente, ele descreve um movimento parabólico em
relação à Terra. De acordo com o princípio da simultaneidade, o lançamento horizontal é
o resultado da composição de dois movimentos simultâneos e independentes.

3. Alcance
𝐴=𝑣0𝒙 ⋅𝑡
Nesse tipo de movimento, é comum que se calcule o alcance (A)
que o corpo atinge na horizontal. Para isso, pode-se usar a
função horária da posição do MU.

4. Tempo de Queda
ou
Para calcular o alcance do corpo, é preciso saber o tempo de
queda, informação que pode ser obtida com o uso das equações
do MUV para a queda livre.

5. Velocidade das componetes
𝑣𝑟=√𝑣𝑥
2
+𝑣𝑦
2
O módulo da velocidade resultante no solo é dado pelo teorema
de Pitágoras:

6. Exemplo:
No instante t = 0, uma partícula é lançada horizontalmente, com velocidade inicial, cujo módulo é 40 m/s, de
um ponto situado a 180 m acima do solo (suposto horizontal), numa região onde a aceleração da gravidade
tem intensidade g = 10 m/s². Despreze os efeitos do ar e adote um sistema de coordenadas de origem O, como
mostra a figura.
Determine:
a) a equação horária da componente vertical da velocidade da partícula;
b) o módulo da velocidade da partícula no instante t = 3,0 s;
c) o instante em que a partícula toca o solo;
d) o alcance horizontal A;

7. Lançament
o Oblíquo
Profº: Gean Costa

8. O que é?
O lançamento oblíquo é o movimento em que o corpo é lançado com o vetor
velocidade formando um ângulo em relação ao eixo horizontal.

9. Velocidade
De acordo com a regra de decomposição de vetores, as componentes da
velocidade na horizontal (x) e na vertical (y) são:
𝒗𝒙=𝒗𝟎⋅𝐜𝐨𝐬𝜽

10. Tempo de subida
𝑡𝑠=
𝒗𝟎 ⋅ 𝐬𝒆𝒏𝜽
𝑔
Tempo total
𝑡𝒕𝒐𝒕𝒂𝒍=
𝟐 𝒗𝟎⋅𝐬𝒆𝒏𝜽
𝑔

11. Alcance
Entre os movimentos anteriores, foi visto que a equação utilizada para obter o
valor do alcance horizontal é:
A = vₒx t
∙
Substituindo o tempo pelo tempo total do movimento para o lançamento
oblíquo e a velocidade pela velocidade na direção horizontal, tem-se:
𝑨=
𝑣0
2
⋅𝐬𝒆𝒏(𝟐 𝜽)
𝑔

12. Alcance
Matematicamente, o alcance horizontal tem relação direta com o valor do ângulo
de lançamento, isto é, alguns ângulos proporcionam alcances maiores que
outros.

13. Altura máxima
Considerando que na altura máxima a velocidade do corpo será nula
verticalmente, a equação da altura máxima para o lançamento oblíquo é:
𝑯=
𝑣0
2
⋅𝐬𝒆𝒏²(𝜽 )
𝟐𝑔

14. Exemplo:
1 - Uma partícula foi lançada com velocidade Vo formando um ângulo de 30° com a direção horizontal, numa
região onde g = 10 m/s². Calcule |Vo|, sabendo que a partícula atinge o vértice de sua trajetória 8,0 segundos
após o lançamento. (Despreze os efeitos do ar.)
2 - Um projétil é lançado obliquamente no ar, com velocidade inicial Vo = 20 m/s, a partir do solo. No ponto
mais alto de sua trajetória, verifica-se que ele tem velocidade igual a metade de sua velocidade inicial. Qual a
altura máxima, em metros, atingida pelo projétil? (Despreze a resistência do ar.)

15. Atividades
1 - Um garoto sentado no chão lança uma bolinha de gude na direção de um buraco situado a 2 m de
distância, em um terreno horizontal. A bolinha parte do solo em uma direção que faz um ângulo de 45° acima
da horizontal. Despreze a resistência do ar. Para que a bolinha caia dentro do buraco, o módulo da velocidade
inicial de lançamento, em m/s, deve ser: (Dado: g = 10 m/s².)
2 - Considere uma pedra sendo lançada horizontalmente do alto de um edifício de 125,0 m de altura, em um
local onde o módulo da aceleração da gravidade é igual a 10 m/s2 e tendo um alcance horizontal igual a 10,0
m. Nessas condições, conclui-se que a velocidade com que a pedra foi lançada, em m/s, é igual a

16. Bons
estudos!
Prof°: Gean Costa