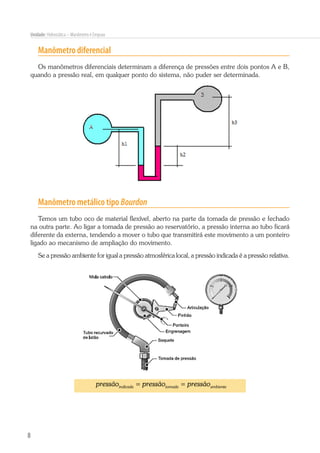
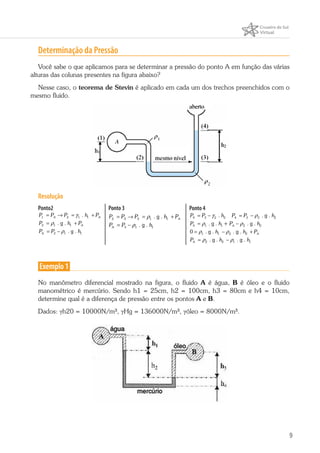
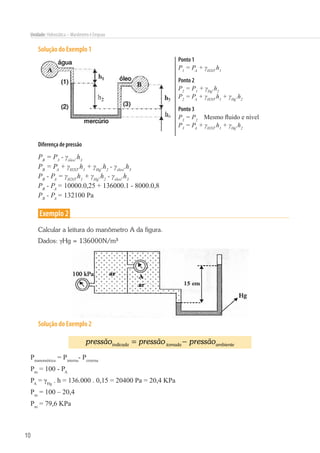
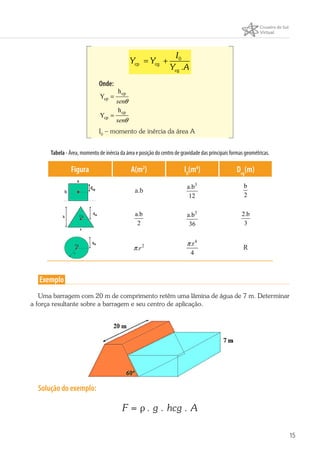
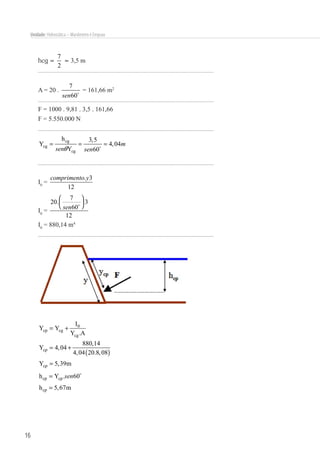
Este documento discute conceitos de hidrostática como manômetros, empuxo e pressão. Explica como manômetros como piezômetros, tubos em U e manômetros diferenciais medem pressão e como o princípio de Arquimedes define empuxo como igual ao peso do fluido deslocado. Também mostra como calcular força resultante em superfícies planas.

1. Hidráulica Geral

3. Material Teórico
Responsável pelo Conteúdo:
Profa. Esp. Viviane Milani Manarini
Revisão Textual:
Profa. Esp. Márcia Ota
Hidrostática – Manômetro e Empuxo

5. 5
• Medidores de Pressão (Manômetros)
• Empuxo
Nesta Unidade, abordaremos sobre manômetros e empuxo, tendo como principal
objetivo calcular as Pressões positivas e negativas e a Ação de fluidos sobre
superfícies submersas. Ex.: barragens.
Leia, atentamente, o conteúdo desta Unidade, que lhe possibilitará conhecer os conceitos
de fluido e o comportamento de um fluido em uma condição de equilíbrio estático como os
medidores de pressão (manômetros) e o empuxo.
Você também encontrará nesta Unidade uma atividade composta por exercícios, relacionada
com o conteúdo estudado. Além disso, terá a oportunidade de refletir sobre seus conhecimentos
e expor na atividade reflexiva que tem a proposta de introduzir o aluno num repertório criativo,
cultural e educativo.
É extremante importante que você consulte os materiais complementares, pois são ricos
em informações, possibilitando-lhe o aprofundamento de seus estudos sobre este assunto.
Hidrostática – Manômetro e Empuxo

6. 6
Unidade: Hidrostática – Manômetro e Empuxo
Contextualização
Para iniciar os estudos desta Unidade, a partir da ilustração abaixo, reflita sobre a questão
do conceito do empuxo:
O Mar Morto (que é, na verdade, um lago famoso por sua lama) recebe esse nome devido à
inexistência de vida naquele ambiente. Isso ocorre pelo alto grau de salinidade de sua água. A
água salgada é mais densa que a água doce; no caso do Mar Morto, a densidade é maior ainda.
Como o empuxo é diretamente proporcional à densidade do líquido, no Mar Morto, corpos
mergulhados ficam submetidos a um grande empuxo e boiam facilmente (figura 1).
Figura1: Um corpo boiando facilmente no Mar Morto .
Fonte:Wikimedia Commons
Conforme a demonstração, analise:
»» O nível é alterado conforme o tipo de corpo mergulhado?
»» O empuxo no corpo varia com a profundidade?

7. 7
Medidores de Pressão (Manômetros)
Na hidráulica, no que se refere a medidores de pressão, ou seja, os manômetros, os mais
usados são:
»» piezômetro;
»» tubo em U;
»» manômetro diferencial; e
»» manômetros analógicos e digitais.
A seguir, vamos conhecer cada um dos medidores de pressão mencionados anteriormente!
Piezômetro
É um tubo de vidro ligado numa extremidade ao ponto do qual se quer medir a pressão e
na outra aberto à atmosfera.
Na realidade, o piezômetro permite a leitura da carga de pressão, mas já sabemos que esta
multiplicada pelo γ do fluido determina a pressão.
Lei de Stevin: .AP hγ=
Tubo em U
Neste manômetro, corrigimos o problema das pressões negativas, pois é possível a formação
de cargas de pressão negativas, isto é, o fluido no ramo direto localizar-se abaixo do nível de
referência A.
Lei de Stevin:
.AP hγ= −
PC
= PA
+ γ.h
mas Pc
= Patm
= 0 (escala relativa)
0 = PA
+ γ.h

8. 8
Unidade: Hidrostática – Manômetro e Empuxo
Manômetro diferencial
Os manômetros diferenciais determinam a diferença de pressões entre dois pontos A e B,
quando a pressão real, em qualquer ponto do sistema, não puder ser determinada.
Manômetro metálico tipo Bourdon
Temos um tubo oco de material flexível, aberto na parte da tomada de pressão e fechado
na outra parte. Ao ligar a tomada de pressão ao reservatório, a pressão interna ao tubo ficará
diferente da externa, tendendo a mover o tubo que transmitirá este movimento a um ponteiro
ligado ao mecanismo de ampliação do movimento.
Se a pressão ambiente for igual a pressão atmosférica local, a pressão indicada é a pressão relativa.
indicada tomada ambientepressão pressão pressão= =

9. 9
Determinação da Pressão
Você sabe o que aplicamos para se determinar a pressão do ponto A em função das várias
alturas das colunas presentes na figura abaixo?
Nesse caso, o teorema de Stevin é aplicado em cada um dos trechos preenchidos com o
mesmo fluido.
Resolução
Ponto2
1 2 1 1
2 1 1
A 2 1 1
Ponto 2
.
. g .
. g .
A A
A
P P P h P
P h P
P P h
γ
ρ
ρ
= → = +
= +
= −
Ponto 3
2 3 2 1 1
A 3 1 1
Ponto 3
. g .
. g .
AP P P h P
P P h
ρ
ρ
= → = +
= −
Ponto 4
4 3 2 2 4 3 2 2
4 1 1 2 2
1 1 2 2
A 2 2 1 1
. . g .
. g . + . g .
0 . g . . g .
. g . . g .
A
A
P P h P P h
P h P h
h h P
P h h
γ ρ
ρ ρ
ρ ρ
ρ ρ
= − = −
= −
= − +
= −
Exemplo 1
No manômetro diferencial mostrado na figura, o fluido A é água, B é óleo e o fluido
manométrico é mercúrio. Sendo h1 = 25cm, h2 = 100cm, h3 = 80cm e h4 = 10cm,
determine qual é a diferença de pressão entre os pontos A e B.
Dados: γh20 = 10000N/m³, γHg = 136000N/m³, γóleo = 8000N/m³.

10. 10
Unidade: Hidrostática – Manômetro e Empuxo
Solução do Exemplo 1
Ponto 1
P1
= PA
+ γH2O
.h1
Ponto 2
P2
= P1
+ γHg
.h2
P2
= PA
+ γH2O
.h1
+ γHg
.h2
Ponto 3
P3
= P2
Mesmo fluido e nível
P3
= PA
+ γH2O
.h1
+ γHg
.h2
Diferença de pressão
PB
= P3
- γóleo
.h3
PB
= PA
+ γH2O
.h1
+ γHg
.h2
- γóleo
.h3
PB
- PA
= γH2O
.h1
+ γHg
.h2
- γóleo
.h3
PB
- PA
= 10000.0,25 + 136000.1 - 8000.0,8
PB
- PA
= 132100 Pa
Exemplo 2
Calcular a leitura do manômetro A da figura.
Dados: γHg = 136000N/m³
Solução do Exemplo 2
indicada tomada ambientepressão pressão pressão= −
Pmanométrica
= Pinterna
- Pexterna
Pm
= 100 - PA
PA
= γHg
. h = 136.000 . 0,15 = 20400 Pa = 20,4 KPa
Pm
= 100 – 20,4
Pm
= 79,6 KPa

11. 11
Empuxo
São forças que agem sobre corpos total ou parcialmente submersos. Seja um corpo
totalmente submerso num fluido de peso específico y.
Além disso, podemos fazer a descrição que, na posição vertical, as pressões na parte inferior
do corpo são maiores que as pressões na parte superior.
Agora, para ampliarmos nossos conhecimentos vamos conhecer o Princípio de Arquimedes:
“A resultante das forças de pressão que
agem num corpo imerso num fluido é
uma força vertical ascendente chamada
empuxo, cujo módulo é igual ao peso do
volume do fluido deslocado.”
Após, vamos estudar sobre a Demonstração do Princípio de Arquimedes:
O Princípio de Arquimedes permite calcular a força que um fluido (líquido ou gás) exerce
sobre um sólido nele mergulhado.
Você gostaria de entender melhor o Princípio de Arquimedes? Então, imagine um copo
totalmente cheio d’água e uma esfera de chumbo.
Importante notar que se a esfera for colocada na superfície da água, ela afundará e ainda
irá provocar o extravasamento de uma certa quantidade de água. Além disso, a força exercida
pela água sobre a esfera terá direção vertical, sentido para cima e módulo igual ao do peso da
água que foi deslocada como mostra a figura a seguir:
Tendo em vista o que já estudamos, segundo o Princípio de Arquimedes, o empuxo é igual
ao peso do líquido deslocado. Dessa forma, é possível escrever que:

12. 12
Unidade: Hidrostática – Manômetro e Empuxo
.L LE W E m g= → =
Onde:
E = empuxo
mL
= a massa do líquido deslocado
Considerando a massa específica, temos:
. .L LE V gρ=
Onde:
ρL
= massa específica do líquido
VL
= volume de líquido deslocado
Exemplo
Um objeto com massa de 20kg e volume de 0,002m³ está totalmente imerso
dentro de um reservatório de água (rH2O = 1000kg/m³), determine:
a) Qual é o valor do peso do objeto? (utilize g = 10m/s²)
b) Qual é a intensidade da força de empuxo que a água exerce sobre o
objeto?
c) Qual o valor do peso aparente do objeto quando imerso na água?
Solução do Exemplo
a) Peso do Corpo:
PC
= m . g
PC
= 20 . 10
PC
= 200 N
b) Empuxo:
E = ρ . g . Vc
E = 1000 . 10 . 0,002
E = 20 N
c) Peso Aparente
PA
= PC
– E
PA
= 200 – 20
PA
= 180 N
Agora que você já conheceu um pouco sobre a demonstração do Princípio de Arquimedes, vamos
estudar sobre a Força resultante e centro de pressão em superfícies planas horizontais.
Você sabia que uma substância, quando em repouso, não resiste às tensões de cisalhamento?
Além disso, conclui-se que a hipótese de repouso nos leva à conclusão da inexistência de
forças tangenciais.
Dessa maneira, temos que as forças estão presentes nas superfícies.
Assim, a força agirá sobre a superfície da área por estar distribuída uniformemente pela
pressão recebida.

13. 13
Força resultante = Pressão x Área
A pressão sobre a superfície plana será a mesma em todos os seus pontos e agirá
perpendicularmente a ela.
Sendo assim, a força resultante atuará verticalmente no centro de pressão da superfície, que
no caso, coincide com o seu centro de gravidade.
Exemplo
Qual é força sobre um comporta quadrada (1 x 1m) instalada no fundo de um reservatório
de água de 2 m de profundidade (ρágua
=1.000 kg/m3
).
P = ρ . g . h = 1000. 9,81 . 2
P = 19.620 Pa
F = P.A
F = 19620 . 1
F = 19.620 N
Já ampliamos bastante nosso conhecimento. Mas ainda não terminamos! Por isso, vamos
estudar sobre: Força resultante e centro de pressão em superfícies planas inclinadas.
Que tal começarmos pela afirmação abaixo?
A força devida à pressão de um líquido que age numa das faces de uma superfície plana
submersa é igual ao produto da pressão agente no centro de gravidade da superfície pela área
da mesma.
O centro de aplicação é considerado como centro de pressão e não coincide com o centro
de gravidade.
Para a determinação da força resultante em uma superfície inclinada, utiliza-se a equação abaixo:
Força resultante = Pressão x Área

14. 14
Unidade: Hidrostática – Manômetro e Empuxo
Para a determinação da posição do centro de pressão e do momento de inércia da área,
utiliza-se a equação Ycp e a Tabela apresentada.
F = ρ . g . hcg . A
Onde:
hcg – profundidade do centro de gravidade da
superfície imersa
Chegou a hora de estudarmos sobre o Ponto de atuação da força
Reflita
O que é o ponto de atuação da força resultante e onde ele age?
Refletiu? Que bom! Podemos, então, verificar se sua reflexão está correta! Confira:
Ponto de atuação da força resultante é o ponto de aplicação da força resultante das
pressões que agem numa superfície submersa.
Pelo conceito de resultante, verifica-se fisicamente que o ponto de aplicação da força deverá
estar deslocado para baixo em relação ao centro de gravidade.

15. 15
0
cp cg
cg .
I
Y Y
Y A
= +
Onde:
cp
cp
h
Y
senθ
=
cp
cp
h
Y
senθ
=
I0
– momento de inércia da área A
Tabela - Área, momento de inércia da área e posição do centro de gravidade das principais formas geométricas.
Figura A(m2
) I0
(m4
) Dcg
(m)
a.b
3
a.b
12
b
2
a.b
2
3
a.b
36
2.b
3
2
.rπ
4
.r
4
π
R
Exemplo
Uma barragem com 20 m de comprimento retém uma lâmina de água de 7 m. Determinar
a força resultante sobre a barragem e seu centro de aplicação.
Solução do exemplo:
F = ρ . g . hcg . A

16. 16
Unidade: Hidrostática – Manômetro e Empuxo
hcg =
7
2
= 3,5 m
A = 20 .
7
60sen 
= 161,66 m2
F = 1000 . 9,81 . 3,5 . 161,66
F = 5.550.000 N
cg
cg
cg
h 3,5
Y 4,04
Y 60
m
sen senθ
= = =
I0
=
. 3
12
comprimento y
I0
=
7
20. 3
60
12
sen
 
  
I0
= 880,14 m4
0
cp cg
cg
I
Y Y
Y .A
= +
( )cp
880,14
Y 4,04
4,04 20.8,08
= +
cpY 5,39m=
cp cph Y . 60sen= 
cph 5,67m=

17. 17
Material Complementar
Para complementar os conhecimentos adquiridos nesta Unidade, leia as seguintes obras:
Livros:
VALADARES, E.C., MATEUS, A.L., SILVA, J.D. Aerodescobertas: explorando novas
possibilidades
Sites:
Caderno Brasileiro de Ensino de Física, disponível em:
http://www.fsc.ufsc.br/ccef
Sociedade Brasileira de Física, responsável pelas publicações Revista Brasileira de Ensino
de Física e Física na escola, disponível em:
http://www.sbfisica.org.br
Feira de Ciências, site com muitas atividades experimentais simples de serem reproduzidas,
disponível em:
http://www.feiradeciencias.com.br
Todas essas sugestões enriquecerão sua compreensão acerca da temática proposta na
unidade. Por isso, não deixe de consultá-las!

18. 18
Unidade: Hidrostática – Manômetro e Empuxo
Referências
AZEVEDO NETTO, J. M. Manual de hidráulica. 8. ed. São Paulo: Edgard Blucher, 1998.
FOX, R. W. Introdução à mecânica dos fluidos. 5. ed. Rio de Janeiro: LTC. 2001.
MUNSON, B. R. Fundamentos da mecânica dos fluidos. 2. ed. São Paulo: Edgard
Blucher, 1997.
BRUNETTI, F. Mecânica dos Fluidos. 2 ed. São Paulo. Pearson.

19. 19
Anotações