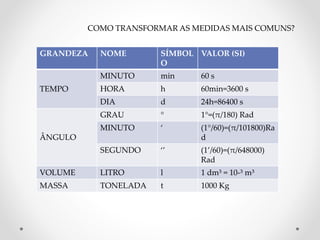
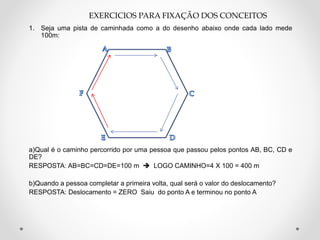
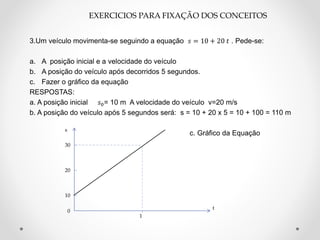
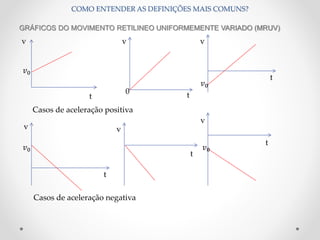
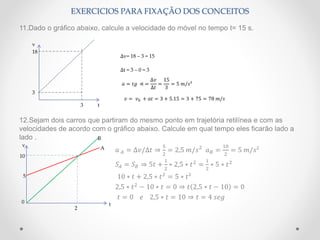
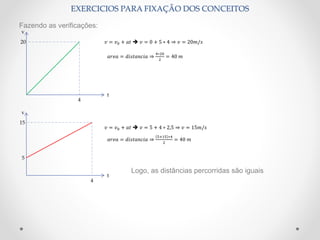
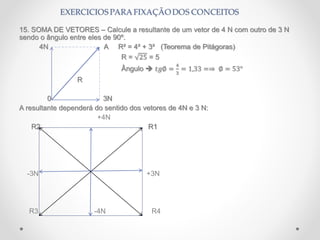
Este documento fornece uma introdução básica aos conceitos fundamentais da física, incluindo o sistema internacional de unidades, pontos e corpos materiais, repouso e movimento, velocidade média e instantânea, aceleração e equações do movimento retilíneo uniforme e uniformemente variado. Exemplos numéricos são fornecidos para reforçar a compreensão dos conceitos.