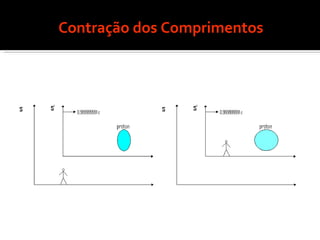
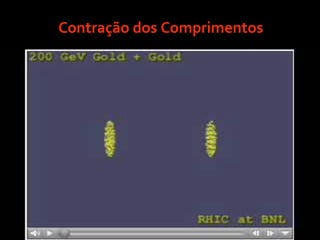
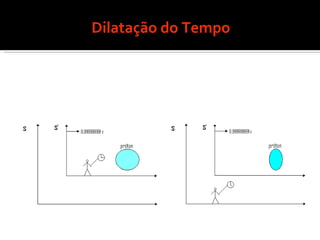
Este documento discute os principais conceitos da relatividade restrita de Einstein, como: 1) A história do desenvolvimento da teoria e a rejeição do conceito de éter; 2) As transformações de Lorentz que relacionam diferentes referenciais inerciais; 3) Os efeitos da contração dos comprimentos e da dilatação do tempo previstos pela teoria.

1. Universidade Federal do Rio Grande Acadêmicos: Cesar Eduardo Krumreich Kauê Bandeira Rodrigues A Relatividade no LHC

2. Tópicos Abordados  Um Pouco de História...  Transformadas de Lorentz  Contração dos Comprimentos  Dilatação do Tempo  Simultaneidade  Paradoxo dos Gêmeos  Relação Entre a Massa e Energia

3. Um Pouco de História... A Relatividade Restrita publicada por Einstein em 1905, descreve a física do movimento na ausência de campos gravitacionais. Ele tenta neste artigo, publicado em 1905, a todo custo, preservar as idéias clássicas pré-existentes e compatibilizar a Teoria Eletromagnética e a Mecânica Clássica de Newton para situações de velocidades muito altas, próximas à da luz.

4. Um Pouco de História... Newton acreditava em um tempo absoluto, que seria como uma espécie de tempo universal, onipotente, quase divino - o mesmo para todos, em todos os lugares . Ele acreditava também em um espaço absoluto, que por sua própria natureza e em relação a qualquer coisa externa, sempre permanecia similar e imóvel.

5. Um Pouco de História... Mas para que houvesse um tempo e espaço absoluto deveria existir um meio em que a luz se propagasse. Essa meio era denominado éter. Para os Gregos o Éter(aethér) significava, primitivamente, uma espécie de fluido sutil e rarefeito que preenchia todo o espaço e envolvia toda a terra.

6. Um Pouco de História... Assim, durante séculos, negar a existência do éter seria a maior asneira possível. No entanto, em fins do século XIX, o físico norte-americano Albert Abraham Michelson , começou a questionar a existência real do éter.

7. Um Pouco de História... Ele inventou um instrumento capaz de medir a velocidade da luz - o interferômetro de Michelson - e de comparar o intervalo de tempo gasto por dois feixes emitidos de uma mesma fonte em duas direções perpendiculares. Com o experimento chegou-se a conclusão de que o éter mostrou não ter qualquer efeito sobre a velocidade da luz .

8. Um Pouco de História... A visão de Newton sobre o tempo o mantinha separado do espaço. Porém, quando Albert Einstein introduziu sua Teoria da Relatividade no começo do século 20, ele sugeriu que tempo e espaço não eram separados, mas sim que estavam interligados. Tempo e espaço se combinavam para formar o espaço-tempo , e todos mediriam suas experiências nele de maneira diferente porque a velocidade da luz é a mesma para todos os observadores.

9. Um Pouco de História... Então, Einstein postulou que:  As leis da física são as mesmas em todos os referenciais inerciais, ou seja, não existe um referencial absoluto.  A velocidade de propagação da luz no espaço livre tem o mesmo valor para todos os observadores, não importando o movimento da fonte ou do observador, ou seja, a rapidez de propagação da luz é uma constante.

10. Um Pouco de História... De acordo com a teoria do eletromagnetismo, de Maxwell , a velocidade da luz e de outras ondas eletromagnéticas é: onde são ,respectivamente, a permissividade e a permeabilidade do vácuo.

11. Transformadas de Lorentz Hendrik Antoon Lorentz em 1904 deixou seu nome às transformações de Lorentz, que formam a base da teoria da relatividade restrita de Einstein.

12. Transformadas de Lorentz Usando os postulados de Einstein para achar a relação geral entre as coordenadas x,y e z a coordenada tempo t de um evento num referencial S, e as seguintes coordenadas x’,y’ e z’ e a coordenada tempo t’ de um evento no referencial S’, que esta com velocidade uniforme em S. Consideramos um caso simples em que as origens coincidem t=t’=0.

13. Transformadas de Lorentz Visto que, devemos utilizar as transformadas de Galileu e que elas deveriam ser corrigidas para suprir as exigências do postulado de Einstein e além disso, considerar que uma onda se propaga no vácuo esfericamente e tomar outras considerações chegamos a conclusão que:

14. Transformadas de Lorentz O LHC (Large Hadron Collider), acelera prótons com um velocidade de 0,999999991c, devido a essa grande velocidade devemos fazer correções Relativisticas. Portanto, a Relatividade tem um papel importante no LHC, pois sem a consideração dela os erros nos cálculos seriam muito grandes. Calculando o fator gama obtemos:

15. Contração dos Comprimentos O que ocorre é que o comprimento medido num referencial em que o objeto está em repouso é o comprimento próprio, dado por . E em um referencial em que o corpo está em movimento, o comprimento que se mede é menor que o comprimento próprio.

16. Contração dos Comprimentos

17. Contração dos Comprimentos

18. Contração dos Comprimentos No LHC o Próton viaja com uma velocidade de cerca 0,999999991c, sendo que o diâmetro do Próton é igual a , ficamos com um comprimento de:

19. Contração dos Comprimentos

20. Dilatação do Tempo A dilatação dos tempos nos diz que sempre quando medimos o intervalo de tempo em um referencial em que os eventos ocorrem em um mesmo local é sempre menor do que o intervalo de tempo entre os mesmos eventos medidos em um outro referencial onde eventos ocorrem em diferentes locais.

21. Dilatação do Tempo

22. Dilatação do Tempo Um exemplo prático da dilatação dos tempos é o caso do múon. O múon é uma partícula que se forma na atmosfera a partir de raios cósmicos e tem um tempo de decaimento de 2x10-6s. Essa partícula viaja com uma velocidade próxima a da luz, vamos supor que ela viaja a 0,998c.

23. Dilatação do Tempo

24. Simultaneidade Dizemos que dois eventos são simultâneos quando eles ocorrem no mesmo instante de tempo. Por exemplo considerando uma nave 1- um observador vendo o evento (a luz se acendendo) dentro da nave; 2 – um observador que se encontra em outro referencial, observando assim o evento de fora.

25. Simultaneidade  Dois eventos que são simultâneos em um sistema de referência não necessariamente devem ser simultâneos em um sistema que se move em relação ao primeiro.

26. Vídeo

27. Paradoxo dos Gêmeos Imagine dois irmãos gêmeos, um é astronauta e faz uma viajem pela galáxia, enquanto o outro permanece na terra. Agora imagine também que esse astronauta se desloca a uma velocidade igual a velocidade máxima atingida pelo próton no acelerador LHC que é de v=0,999999991c. Quanto tempo você acha que se passou para o astronauta que estava na nave em relação ao seu irmão gêmeo que se encontra na terra, sendo que na terra se passou 10 anos?

28. Paradoxo dos Gêmeos

29. Relação Entre a Massa e Energia Podemos calcular também a energia cinética relativística que cada próton carrega. Esta energia pode ser calculada a partir da relação entre massa-energia. Sabemos que cada próton parado tem uma energia de repouso E 0 dada por:

30. Relação Entre a Massa e Energia A energia total E envolvida corresponde a energia de repouso E 0 mais a energia cinética E C do próton, por estar em movimento. Em termos Práticos podemos escrever que: a massa inercial relativística do próton é diferente da massa de repouso pelo fator gama, ela pode ser escrita como:

31. Relação Entre a Massa e Energia logo, simplificando,obtemos: dado que a massa de repouso do próton é , chegamos a conclusão que a energia cinética disponível no próton é:

32. Relação Entre a Massa e Energia Portanto, a energia total envolvida em uma colisão entre dois prótons pode ser de aproximadamente 14TeV.

33. Referências  Física Conceitual/PaulG.Hewitt;Triste Freire Ricci;Maria Helena Gravina. – 9.ed-Porto Alegre:Bookman,2002.  http://www.youtube.com/watch?v=njToAZrphko  http://ciencia.hsw.uol.com.br/dilatacao-do-tempo1.htm  http://pt.shvoong.com/books/1756214-newton-deus-tempo-s%C3%A3o-absolutos/  http://www.scribd.com/doc/7207736/o-Conceito-de-Espaco-e-Tempo-de-Isaac-Newton