O documento aborda conceitos fundamentais de dinâmica e vibrações em sistemas mecânicos, incluindo geometria de massas, equações diferenciais, sistemas com graus de liberdade e análise de movimentos. São discutidos regimes de vibração livres e forçados, além de métodos para controle de vibrações e análise de roldanas. O conteúdo é substancial e técnico, refletindo o conhecimento necessário para entendimento de sistemas vibratórios e suas aplicações práticas.

1. 1
Contents
Geometria de Massas ...............................................................................................................................................3
Conversões e Relações Trigonométricas ...................................................................................................................5
Equações Diferenciais – Nomenclatura .....................................................................................................................5
Componentes Energéticas .......................................................................................................................................6
Teoremas e Princípios Dinâmicos e Cinemáticos ......................................................................................................6
Sistemas Particulares................................................................................................................................................7
a) Análise de Movimentos Básicos.....................................................................................................................7
b) Análise de Roldanas (Pulley Systems) ............................................................................................................8
1- Sistemas c/ 1 Grau Liberdade .........................................................................................................................10
1.1- Glossário .................................................................................................................................................10
1.2- Introdução ..............................................................................................................................................13
1.3- Regime Livre (Equação Diferencial Ordinária Linear Homogênea)............................................................14
1.2.1- Sistema Subamortecido , 𝟎 ≤ 𝝃 < 𝟏...................................................................................................14
1.2.2- Resposta do Sistema Criticamente Amortecido , 𝝃 = 𝟏.....................................................................15
1.2.3- Resposta do Sistema Sobreamortecido , 𝝃 > 𝟏 .................................................................................15
1.4- Regime Forçado Periódico - Harmônico (E.D.L.O.N.) ................................................................................16
1.4.1- Solicitação Harmónica Ativa - Força Discreta.......................................................................................16
1.4.2 - Solicitação Harmónica Ativa – Rotação de Massas em Desiquilibrio ...................................................18
1.4.3- Solicitação Harmónica Passiva..............................................................................................................19
1.4.4- Isolamento de Vibrações ......................................................................................................................20
1.4.5- Transdutor de Vibrações .......................................................................................................................22
1.5- Regime Forçado Periódico - Não Harmônico............................................................................................24
1.6- Regime Forçado Não Periódico (Impulsiva e transiente) ..........................................................................26
1.7.1- Regime Forçado Impulsivo....................................................................................................................26
1.7.2- Regime Forçado Transiente ..................................................................................................................26
2 - Graus de Liberdade............................................................................................................................................28
2.1- Glossário......................................................................................................................................................28
2.2 – Introdução .................................................................................................................................................38
2.3 – Regime Livre ( Sistemas Não Amortecidos).................................................................................................39
2.4- Regime Forçado Harmônico.........................................................................................................................40
2.4.1 – Introdução...........................................................................................................................................40
2.4.2 – Absorsor de Vibrações.........................................................................................................................41

2. 2
2.5 – Regime Forçado Transiente ........................................................................................................................44
3- Sistemas Contínuos (Equação Diferencial Linear Parcial Homogênea) ................................................................45
3.1- Glossário......................................................................................................................................................45
3.2- Vibração Lateral de Cordas...........................................................................................................................52
3.3- Vibração Longitudinal de Barras..................................................................................................................55
3.4- Vibração Torsional de Veios ........................................................................................................................57
3.5- Vibração lateral de Vigas..............................................................................................................................58
3.6- Metodo Aproximado da Energia de Rayleigh................................................................................................60
3.6.1 – Glossário .............................................................................................................................................60
3.6.2 – Procedimento......................................................................................................................................61
3.7 – Considerações Práticas – Casos Particulares ...............................................................................................63
3.7.1- Resolução Analítica do Problema Característico..................................................................................63
3.7.2- Método de Rayleigh..............................................................................................................................67
4 - Controlo de Vibrações........................................................................................................................................68

3. 3
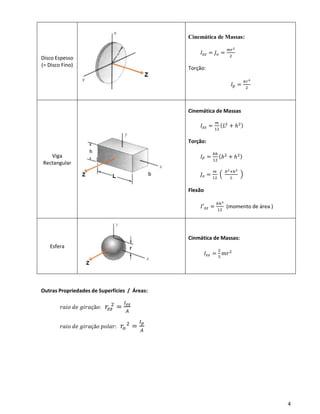
Geometria de Massas
Nomenclatura:
• Momento de 2ª ordem de área - 𝐼′ 𝑥𝑥 , 𝐼′ 𝑦𝑦 , 𝐼′ 𝑧𝑧 [𝑚4
]
• Momento Polar de Área - 𝐼 𝑝 = 𝐼𝑥𝑥 + 𝐼 𝑦𝑦
• Momento de Inércia de massas - 𝐼𝑥𝑥 , 𝐼 𝑦𝑦 , 𝐼𝑧𝑧 [𝑘𝑔 𝑚2
]
• Momento Polar de Inércia de massas - 𝐽 𝑜 = 𝐼 𝑝 𝜌𝑙 (válido para solidos sem desenvolvimento axial !! )
Solido Propriedade - Aplicação
Barra
Esbelta
(Secção
Qualquer)
Cinemática de Massas:
𝐼𝑧𝑧 =
𝑚𝐿2
12
Anel fino
Cinemática de Massas:
𝐼𝑧𝑧 = 𝐽 𝑜 =
𝑚𝑟2
2
Varão Espesso
Cinemática de Massas:
𝐼𝑧𝑧 = 𝐼 𝑦𝑦 =
𝑚
12
(3𝑟2
+ 𝐿2)
Torção:
𝐼 𝑝 =
𝜋𝑟4
2
(momento polar de área)
𝐽 𝑜 = 𝐼𝑥𝑥 =
𝑚𝑟2
2
Flexão:
𝐼′ 𝑧𝑧 =
𝜋𝑟4
4
(momento de área )

4. 4
Disco Espesso
(= Disco Fino)
Cinemática de Massas:
𝐼𝑧𝑧 = 𝐽 𝑜 =
𝑚𝑟2
2
Torção:
𝐼 𝑝 =
𝜋𝑟4
2
Viga
Rectangular
Cinemática de Massas
𝐼𝑧𝑧 =
𝑚
12
( 𝐿2
+ ℎ2)
Torção:
𝐼 𝑃 =
𝑏ℎ
12
( 𝑏2
+ ℎ2)
𝐽 𝑜 =
𝑚
12
(
𝑏2+ℎ2
𝐿
)
Flexão
𝐼′ 𝑧𝑧 =
𝑏ℎ3
12
(momento de área )
Esfera
Cinmática de Massas:
𝐼𝑧𝑧 =
2
5
𝑚𝑟2
Outras Propriedades de Superfícies / Áreas:
𝑟𝑎𝑖𝑜 𝑑𝑒 𝑔𝑖𝑟𝑎çã𝑜: 𝑟𝑧𝑧
2
=
𝐼 𝑧𝑧
𝐴
𝑟𝑎𝑖𝑜 𝑑𝑒 𝑔𝑖𝑟𝑎çã𝑜 𝑝𝑜𝑙𝑎𝑟: 𝑟𝑜
2
=
𝐼 𝑝
𝐴
h
b

5. 5
Conversões e Relações Trigonométricas
• 𝜔 = 𝑟𝑝𝑚 ⋅ π
30
𝜔 = 2𝜋 ⋅ 𝑓𝐻𝑧 𝜔 =
2𝜋
𝑇
𝑓 =
1
𝑇
• 𝑟𝑎𝑑 = 𝛼° ⋅
π
180
𝛼° = 𝑟𝑎𝑑 ⋅
180
π
• sin( 𝜔𝑡) = cos (𝜔𝑡 −
𝜋
2
) − sin( 𝜔𝑡) = cos (𝜔𝑡 +
𝜋
2
) − cos( 𝜔𝑡) = cos( 𝜔𝑡 + 𝜋)
• Agrupamento de funções trignométricas de igual frequência:
Equações Diferenciais – Nomenclatura
𝛼
𝛼
Homogêneas
Não Homogêneas
Lineares
Não Lineares
𝑎 𝑛 𝑦 𝑛
𝑦 + 𝑎𝑦𝑦3
= 𝑘
Ordinárias
𝑎 𝑛 𝑦 𝑛
+ 𝑎 𝑛−1 𝑦 𝑛−1
+ ⋯ + 𝑎1 𝑦 + 𝑎0 = 0
de Derivadas Parciais
𝑎2
𝑑2
𝑑𝑥2 𝑢 + 𝑎1
𝑑
𝑑𝑥
𝑢 + 𝑏2
𝑑2
𝑑𝑡2 𝑢 + 𝑏1
𝑑2
𝑑𝑡
𝑢 + 𝑘 𝑜 = 𝐹
Equações Algébricas
Equações Diferenciais

6. 6
Componentes Energéticas
• Variação Energia Potencial: 𝑉 = ∑ 𝑚 𝑖 𝑔 (ℎ 𝐺 𝑖
|1 − ℎ 𝐺 𝑖
|0)𝑛
𝑖 + ∑
𝑘
2
[ ( 𝑥2 − 𝑥1)2
|1 − ( 𝑥2 − 𝑥1)2
|0 ]𝑁
𝑗
• Variação Energia Cinética 𝑇 = ∑
𝑚
2
(𝑥̇ 𝐺
2
|1 − 𝑥̇ 𝐺
2
|0) +
𝐽
2
(𝜃̇ 2
|1 − 𝜃̇ 2
|0)𝑛
𝑖
𝑇 = ∑
𝑚 𝑖
2
( 𝑥̇ 𝐺
2
) +
𝐽 𝑖
2
( 𝜃̇ 2
)𝑛
𝑖
• Teorema da Variação da 𝛥𝐸 𝑚𝑒𝑐 = 𝑊𝑓𝑛𝑐 = 𝑊𝑑𝑖𝑠𝑠𝑖𝑝 =
𝑘 𝑒𝑞
2
[ 𝑥𝑡̅
2
− 𝑥0
2
] +
𝑚 𝑒𝑞
2
[ 𝑥̇ 𝑡̅
2
− 𝑥̇0
2
]
Energia Mecânica (TVEM):
( 𝑊𝑓𝑛𝑐 = 𝑊𝑑𝑖𝑠𝑠𝑖𝑝 valido para regime livre ou natural)
• Definição de energia Dissipada: 𝑊𝑑𝑖𝑠𝑠𝑖𝑝 = ∫ 𝐹𝑐( 𝑡) ⋅ 𝑣( 𝑡)1 + 𝐹𝑐(𝑡) ⋅ 𝑣(𝑡)2 𝑑𝑡
𝑡2
𝑡1
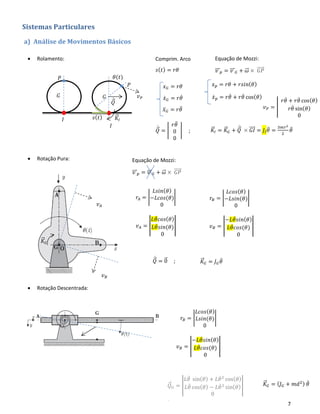
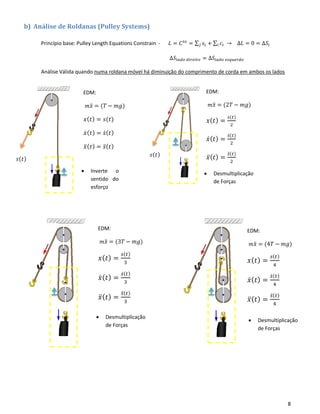
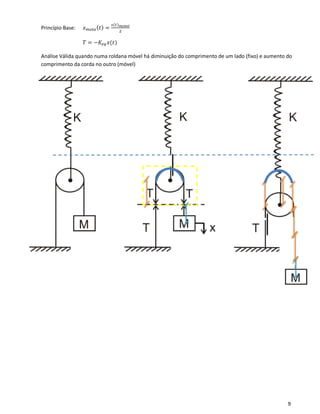
Teoremas e Princípios Dinâmicos e Cinemáticos
• Equação de Mozzi: 𝑣 𝑝⃗⃗⃗⃗ = 𝑣𝑜⃗⃗⃗⃗ + 𝜔⃗⃗ × 𝑂𝑃⃗⃗⃗⃗⃗
• Quantidade de Aceleração: 𝑄⃗̇
= 𝑚𝑣̇ = 𝑚𝑥̈
• Momento Dinâmico: 𝐾𝐺
⃗⃗⃗⃗⃗ = 𝐽 𝐺 ⋅ 𝜃̈
• 2º Teorema de König: 𝐾 𝑂
⃗⃗⃗⃗⃗ = 𝐾 𝐺
⃗⃗⃗⃗⃗ + 𝑂𝐺⃗⃗⃗⃗⃗ × 𝑄⃗̇
• Teorema de Steiner ou
Teorema dos Eixos Paralelos: 𝐽 ′
= 𝐽 𝐺 + 𝑚𝑑2
Para momentos de Inércia
de 2ª ordem
• Teorema de “Steiner” 𝐾𝑜 = 𝐽 𝑜 𝜃̈ = ( 𝐽 𝐺 + 𝑚𝑑2 ) 𝜃̈
Momento Dinâmico:
• Força Impulsiva: 𝐹 = ∫ 𝑓(𝑡) 𝑑𝑡
0+𝛥𝑡
0
= 𝑚𝑥̇0 [N/s]
• Produto Interno Nulo: 𝑢 ⋅ 𝑣 = 0 ⇒ 𝑢 ⊥ 𝑣
• Produto Externo Nulo: 𝑢 × 𝑣 = 0 ⇒ 𝑢 ∥ 𝑣
Instante 0 de referência :
• Equilíbrio Estático
(T=0)
• As molas podem apresentar
pré-tensão
(V elástica=V gravítica) ou não
(V elástica = 0). Apenas serve
para anular a componente da
energia gravítica ou não, mas
nunca é calculada
• Sistemas tipo pêndulo (SEM
pré-tensão nas molas ) é que
apresentam variação da energia
potencial gravítica
válido apenas para pontos G
e O sem movimento relativo

7. 7
Sistemas Particulares
a) Análise de Movimentos Básicos
• Rolamento:
𝐾⃗⃗ 𝐼 = 𝐾⃗⃗ 𝐺 + 𝑄⃗̇
× 𝐺𝐼⃗⃗⃗⃗ = 𝐽𝐼 𝜃̈ =
3𝑚𝑟2
2
𝜃̈
• Rotação Pura:
• Rotação Descentrada:
𝜃(𝑡)
𝐼
𝐼 𝑠( 𝑡)
Comprim. Arco
𝑠( 𝑡) = 𝑟𝜃
𝑥 𝐺 = 𝑟𝜃
𝑥̇ 𝐺 = 𝑟𝜃̇
𝑥̈ 𝐺 = 𝑟𝜃̈
Equação de Mozzi:
𝑣⃗⃗⃗ 𝑝 = 𝑣⃗⃗⃗ 𝐺 + 𝜔⃗⃗ × 𝐺𝑃⃗⃗⃗⃗⃗
𝐺
𝑃
𝑥 𝑝 = 𝑟𝜃 + 𝑟𝑠𝑖𝑛( 𝜃)
𝑥̇ 𝑝 = 𝑟𝜃̇ + 𝑟𝜃̇ cos( 𝜃)
𝑣 𝑃 = |
𝑟𝜃̇ + 𝑟𝜃̇ cos( 𝜃)
𝑟𝜃̇ sin( 𝜃)
0
𝑃
𝐺
𝑄⃗̇
𝑣 𝑃
𝑄⃗̇ = |
𝑟𝜃̈
0
0
| ;
Equação de Mozzi:
𝑣⃗⃗⃗ 𝑝 = 𝑣⃗⃗⃗ 𝐺 + 𝜔⃗⃗ × 𝐺𝑃⃗⃗⃗⃗⃗
𝐾⃗⃗ 𝐼
𝑄⃗̇ = 0⃗ ;
𝐾⃗⃗ 𝐺
𝑟𝐴 = |
𝐿𝑠𝑖𝑛( 𝜃)
−𝐿𝑐𝑜𝑠(𝜃)
0
| 𝑟𝐵 = |
𝐿𝑐𝑜𝑠( 𝜃)
−𝐿𝑠𝑖𝑛(𝜃)
0
|
𝑣 𝐴 = |
𝐿𝜃̇ 𝑐 𝑜𝑠( 𝜃)
𝐿𝜃̇ 𝑠 𝑖𝑛(𝜃)
0
| 𝑣 𝐵 = |
−𝐿𝜃̇ 𝑠 𝑖𝑛( 𝜃)
𝐿𝜃̇ 𝑐 𝑜𝑠(𝜃)
0
|
𝐾⃗⃗ 𝐺 = 𝐽 𝐺 𝜃̈
𝑟𝐵 = |
𝐿𝑐𝑜𝑠( 𝜃)
𝐿𝑠𝑖𝑛(𝜃)
0
|
𝑣 𝐵 = |
−𝐿𝜃̇ 𝑠 𝑖𝑛( 𝜃)
𝐿𝜃̇ 𝑐 𝑜𝑠(𝜃)
0
|
𝑣 𝐴
𝑣 𝐵
𝑄⃗ 𝐺
̇ = |
𝐿𝜃̈ sin( 𝜃) + 𝐿𝜃̇2
cos( 𝜃)
𝐿𝜃̈ cos( 𝜃) − 𝐿𝜃̇2
sin( 𝜃)
0
|
;
𝐾⃗⃗ 𝐺 = ( 𝐽 𝐺 + 𝑚𝑑2) 𝜃̈

8. 8
b) Análise de Roldanas (Pulley Systems)
Princípio base: Pulley Length Equations Constrain - 𝐿 = 𝐶 𝑡𝑒
= ∑ 𝑠𝑖𝑗 + ∑ 𝑐𝑖𝑖 → ∆𝐿 = 0 = ∆𝑆𝑖
∆𝑆𝑙𝑎𝑑𝑜 𝑑𝑖𝑟𝑒𝑖𝑡𝑜 = ∆𝑆𝑙𝑎𝑑𝑜 𝑒𝑠𝑞𝑢𝑒𝑟𝑑𝑜
Análise Válida quando numa roldana móvel há diminuição do comprimento de corda em ambos os lados
• Inverte o
sentido do
esforço
• Desmultiplicação
de Forças
𝑠(𝑡)
𝑠(𝑡)
EDM:
𝑚 𝑥̈ = (2𝑇 − 𝑚𝑔)
𝑥( 𝑡) =
𝑠(𝑡)
2
𝑥̇( 𝑡) =
𝑠̇( 𝑡)
2
𝑥̈( 𝑡) =
𝑠̈( 𝑡)
2
EDM:
𝑚 𝑥̈ = (3𝑇 − 𝑚𝑔)
𝑥( 𝑡) =
𝑠(𝑡)
3
𝑥̇( 𝑡) =
𝑠̇( 𝑡)
3
𝑥̈( 𝑡) =
𝑠̈( 𝑡)
3
EDM:
𝑚 𝑥̈ = (4𝑇 − 𝑚𝑔)
𝑥( 𝑡) =
𝑠(𝑡)
4
𝑥̇( 𝑡) =
𝑠̇( 𝑡)
4
𝑥̈( 𝑡) =
𝑠̈( 𝑡)
4
EDM:
𝑚 𝑥̈ = (𝑇 − 𝑚𝑔)
𝑥( 𝑡) = 𝑠(𝑡)
𝑥̇( 𝑡) = 𝑠̇( 𝑡)
𝑥̈( 𝑡) = 𝑠̈( 𝑡)
• Desmultiplicação
de Forças
• Desmultiplicação
de Forças

9. 9
Princípio Base: 𝑥 𝑚𝑜𝑙𝑎( 𝑡) =
𝑠(𝑡) 𝑚𝑜𝑣𝑒𝑙
2
𝑇 = −𝐾𝑒𝑞 𝑥(𝑡)
Análise Válida quando numa roldana móvel há diminuição do comprimento de um lado (fixo) e aumento do
comprimento da corda no outro (móvel)

10. 10
1- Sistemas c/ 1 Grau Liberdade
1.1- Glossário
• Vibração (mecânica) – Movimento alternado ou oscilatório relativamente a uma posição de referênica
(equilibrio estático), envolvendo a continua conversão de energia potencial em energia cinética, com ou
sem dissipação de energia. A vibração pode ser :
Livre (Natural) Não Amortecida
Forçada Amortecida
• Sistema Vibratório – Sistema mecânico, que oscila em torno de uma posição de referência (equilibrio
estático), convertendo continuamente energia cinética em energia potencial (e vice-versa), com ou sem
dissipação de energia. Para tal é geralmente constituido por:
elemento elástico – componente com capacidade de armazenar energia potencial
massa ou inércia – componenete com capacidade de armazenar energia cinética
amortecedor – componente dissipador de energia
O sistema mecânico vibratório pode ser classificado em:
Contínuo – Sistema com um número infinito de graus de liberdade
Discrreto – Sistema com um número finito de graus de liberdade
• Grau de Liberdade – Coordenada independente necessária para determinar a posição de um
componente do sistema vibratório em qualquer instante (descrever a cinemática do sistema).
• Excitação – Solicitação dinâmica externa, perturbação cuja fonte de energia pode apresentar-se sob a
forma de uma força dinâmica aplicada directamente (transmissao ativa) e/ou deslocamento imposto
(transmissao passiva). A excitação pode ser classificada em:
Periódica Harmônica *
Determinística Não Harmônica *
Não Periódica Impulsiva *
Transiente *
Não determinística
• Frequência Natural – Frequência à qual o sistema vibra em regime Livre / Natural. Existe a frequência
natural não amortecida ( 𝜔 𝑛 sistema não amortecido) e frequência natural amortecida ( 𝜔 𝑑 sistema sub-
amortecido ). A frequência natural é uma propriedade intrínseca do sistema.
• Frequência de Ressonância – Frequência de excitação, para a solicitação harmônica, para a qual o
sistema apresenta uma maior amplitude da resposta.
• Regime Livre / Natural – Vibração de um sistema mecânico devido exclusivamente a uma perturbação
inicial de deslocamento e/ou velocidade. Não havendo qualquer solicitação dinâmica exterior.
• Regime Forçado – Vibração de um sistema mecânico sujeito a uma solicitação dinâmica exterior.

11. 11
• Estabilidade do movimento – Capacidade de o sistema tender para a resposta forçada pela entrada, isto
é, os termos associados à dinâmica do próprio sistema tendem para zero ou estão limitados.
• Equação Característica – Obtida a partir do plug-in da solução não trivial na EDM
𝑚𝑠2
+ 𝑐𝑠 + 𝑘 = 0 , 𝑥( 𝑡) = 𝐶𝑒 𝑠𝑡
• Caracterização das Soluções da Eq. Característica ( 𝑚𝑠2
+ 𝑐𝑠 + 𝑘 = 0 )
Natureza das
Soluções
Razao de
Amortecimento
Classificação do
Sistema Vibratório
Caracterização do
movimento de
resposta
Estabilidade
Raizes Distintas,
Complexas
imaginárias puras
𝜉 = 0
Sistema não
Amortecido
Movimento
harmônico
Marginalmente
Estável
Ou estável
Raizes Distintas,
Complexas
conjugadas
0 < 𝜉 < 1
Sistema
Sub-amortecido
Movimento oscilatório
com atenuação
exponencial da
amplitude
Estável ou
assimptoticamente
estávelRaiz Dupla,
real e negativa
𝜉 = 1
Sistema
criticamente
Amortecido
Movimento Não
Oscilatório com
atenuação
exponencialRaizes Distintas,
reais e negativas
𝜉 > 1
Sistema
Sobre-amortecido
Localização Geométrica das
Soluções (em função de 𝜉 ) no
Plano de Argand-Gauss

12. 12
• Método do Decremento logorítmico – Método experimental de determinação da razão de
amortecimento de um sistema vibratório com 1 G.L. O procedimento consiste em:
Medição da resposta do sistema (resposta real)
Registo da resposta entre instantes separados por um número inteiro de ciclos 𝑥(𝑡) e 𝑥(𝑡 + 𝑁𝑇 )
Calculo do decremento logarítmico, 𝛿 = ln (
𝑥(𝑡)
𝑥(𝑡+𝑁𝑇)
)
Calculo da razão de amortecimento, 𝜉 = 𝑓(𝛿)
• Método da Energia de Rayleigh – Método aproximado de determinar a frequência natural fundamental
de vibração de um sistema mecânico. Pressupostos:
- Sistema não Amortecido (Sistema Conservativo)
- Resposta de um Sistema nao Amortecido: 𝑥( 𝑡) = 𝐴𝑐𝑜𝑠(𝜔𝑡 − 𝜑)
- Princípio da Conservação da Energia Mecânica: 𝑇 𝑚𝑎𝑥 = 𝑉𝑚 𝑎𝑥
• Isolamento de Vibrações – Consiste em reduzir a :
o Transmissão ativa – forças dinâmicas transmitidas de equipamentos moveis (massa sujeita a uma
solicitação dinamica externa ou rotor com Cg excentrico) para os seus apoios
o Transmissão passiva – movimento transmitido para os equipamentos pelas suas bases móveis
(ex: aparelho de medição em mesa laboratorial)
• Harmônico – Função Harmônica resultante da expansão de uma função periódica, em serie de Fourier
• Harmônico principal – Função harmônica resultante da expansão de uma função periódica, em serie de
Fourier, com frequência igual à frequênica da função expandida
• Força Impulsiva –
• Choque – Excitação ou solucitação dinâmica externa, transiente, caracterizada por:
o Grandeza elevada
o Tempo de actuação 𝑡 𝑐 muito inferior ao periodo de resposta do sistema em regime livre
• Frequência Natural nula
– Movimento de corpo rígido (disco rolante, )
– Situação de Instabilidade (barra sujeita a compressão num modelo barra massa concentrada)

13. 13
1.2- Introdução
• Teoremas Vetoriais da Dinâmica (TVD): ∑ 𝐹 = ∑ 𝑄⃗̇
𝑖𝑗
∑ 𝑀 𝑂 = ∑ 𝐾 𝑂
⃗⃗⃗⃗⃗𝑖𝑗
• Equação Diferencial do Movimento (EDM):
1 G.L Linear ( ∑ 𝑚𝑖𝑖 ) 𝑥̈ ( ∑ 𝑐𝑓𝑓 ) 𝑥̇ + (∑ 𝑘𝑗𝑗 + ∑
𝑚 𝑖 𝑔
𝑙𝑖 ) 𝑥 = 𝑘𝑠( 𝑡) + 𝑐𝑠̇( 𝑡)
1 G.L Angular ( ∑ 𝑚𝑖𝑖 𝑙2 ) 𝜃̈ + ( ∑ 𝑐𝑓𝑓 𝑙2 ) 𝜃̇ + ( ∑ 𝑘𝑗𝑗 𝑙2
+ ∑ 𝑚𝑖𝑖 𝑔𝑙 ) 𝜃 = 𝑙 ⋅ 𝑘𝑠( 𝑡) + 𝑙 ⋅ 𝑐𝑠̇( 𝑡) + 𝐹𝑙 ⋅
𝑐𝑜𝑠( 𝜔𝑡)
[𝑁𝑠2
/𝑚] [𝑁𝑠/𝑚] [𝑁/𝑚] + [𝑁]
𝑘𝑔 𝑐 𝑘 𝑚𝑔
[𝐾𝑔] =
[𝑁𝑠2
/𝑚]
[𝑔] =
[𝑚/𝑠2]
1 G.L Torsional ( ∑ 𝐽𝑖𝑖 ) 𝜃̈ + ( ∑ 𝑐𝑡 𝑓𝑓 ) 𝜃̇ + ( ∑ 𝑘𝑡 𝑗𝑗 ) 𝜃 = 𝑀 ⋅ 𝑐𝑜𝑠( 𝜔𝑡)
[𝑁𝑠2
𝑚] [𝑁𝑠 𝑚] [𝑁𝑚]
𝑘𝑔 𝑚2
𝑐𝑡 𝑘𝑡
Propriedades de Vibração do Sistema :
• Frequência Natural não amortecida: 𝜔 𝑛 = √
𝑘 𝑒𝑞
𝑚 𝑒𝑞
; 𝑇𝑛 =
2𝜋
𝜔 𝑛
• Frequencia Natural amortecida: 𝜔 𝑑 = 𝜔 𝑛√1 − 𝜉2 ; 𝑇𝑑 =
2𝜋
𝜔 𝑑
• Razão de Amortecimento: 𝜉 =
𝑐 𝑒𝑞
2 𝑚 𝑒𝑞 ⋅ 𝜔 𝑛
• Constante de Amortecimento Crítico: 𝑐 𝑐 = 2 𝑚 𝑒𝑞 ⋅ 𝜔 𝑛
• Obtenção Experimental da Rigidez Equivalente: 𝑘 𝑒𝑞 = 𝑓𝑒𝑠𝑡 ⋅
1
𝑑 𝑒𝑠𝑡
Excitação (velocidade)
Imposta ao Amortecedor
Deslocamento
Imposto à
Mola

14. 14
1.3- Regime Livre (Equação Diferencial Ordinária Linear Homogênea)
• Equação Diferencial do Movimento Base:
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [𝑐 𝑒𝑞] 𝑥̇ + [𝑘 𝑒𝑞] 𝑥 = 0
1.2.1- Sistema Subamortecido , 𝟎 ≤ 𝝃 < 𝟏
• Resposta do Sistema
𝑥( 𝑡) = 𝐴𝑒− 𝜉𝜔 𝑛 𝑡
cos( 𝜔 𝑑 𝑡 − 𝜑) 𝜔 𝑑 = 𝜔 𝑛√1 − 𝜉2
𝑥̇( 𝑡) = −𝐴 ⋅ 𝜔 𝑛 ⋅ 𝑒− 𝜉𝜔 𝑛 𝑡
cos( 𝜔 𝑑 𝑡 − 𝜑 − 𝜓) , 𝐴 = √(
𝑥̇ 𝑜+𝜉𝜔 𝑛 𝑥 𝑜
𝜔 𝑑
)
2
+ 𝑥 𝑜
2
𝜑 = tan−1
(
1
𝑥 𝑜
⋅
𝑥̇ 𝑜+𝜉𝜔 𝑛 𝑥 𝑜
𝜔 𝑑
)
𝜓 = tan−1
(
√1−𝜉2
𝜉
)
• Equações das Envelopes – dependem apenas do amortecimento
𝑦 = 𝐴𝑒−𝜉𝜔 𝑛 𝑡
• Determinação Experimental de ( 𝜉) – Metodo do Decremento Logarítmico (δ) para 0 < 𝜉 < 1
𝛿 =
1
𝑁
ln (
𝑥(𝑡1)
𝑥(𝑡1+𝑁⋅𝑇 𝑑)
) , N=1, 2, 3,.. (nº de ciclos entre as duas medições)
𝜉 =
𝛿
√ 4𝜋2+𝛿2
• Respostas Máxima 𝑥( 𝑡) | 𝑚𝑎𝑥 e Instante em que ocorre 𝑡| 𝑥 𝑚𝑎𝑥
ou Energia Poencial Maxima:
𝑡| 𝑥 𝑚𝑎𝑥
=
1
𝜔 𝑑
(tan−1( 𝐸) + 𝜑) 𝐸 = −
𝜉
√1−𝜉2
𝑥( 𝑡) | 𝑚𝑎𝑥 = 𝐴𝑒 𝐸 [tan−1(𝐸)+𝜑]
cos(tan−1
(𝐸)) (or just plug in the 𝑡| 𝑥 𝑚𝑎𝑥
in the response
expression )
• Velocidade Máxima ou 1ª vez que o sistema passa pela Posição de Equilibrio Estático

15. 15
1.2.2- Resposta do Sistema Criticamente Amortecido , 𝝃 = 𝟏
𝑥( 𝑡) = [ 𝑥̇ 𝑜 + 𝑥0 𝜔 𝑛] 𝑒− 𝜔 𝑛 𝑡
[ 𝑡 +
𝑥 𝑜
𝑥̇ 𝑜+𝑥0 𝜔 𝑛
]
𝑥̇( 𝑡) = [ 𝑥̇ 𝑜 + 𝑥0 𝜔 𝑛] ⋅ 𝜔 𝑛 ⋅ 𝑒− 𝜔 𝑛 𝑡
[
1
𝜔 𝑛
− 𝑡 −
𝑥 𝑜
𝑥̇ 𝑜+𝑥0 𝜔 𝑛
]
1.2.3- Resposta do Sistema Sobreamortecido , 𝝃 > 𝟏
𝑥( 𝑡) = 𝑒− 𝜉𝜔 𝑛 𝑡
[ A1 cosh(𝜔 𝑛√𝜉2 − 1 𝑡) +A2 sinh(𝜔 𝑛√𝜉2 − 1 𝑡) ] A1 = 𝑥 𝑜
𝑥̇( 𝑡) =
𝑑
𝑑𝑡
[𝑥( 𝑡)] A2 =
𝑥̇ 𝑜+𝜉𝜔 𝑛 𝑥 𝑜
𝜔 𝑛√𝜉2−1

16. 16
1.4- Regime Forçado Periódico - Harmônico (E.D.L.O.N.)
1.4.1- Solicitação Harmónica Ativa - Força Discreta
• Equação Diferencial do Movimento Base:
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [𝑐 𝑒𝑞] 𝑥̇ + [𝑘 𝑒𝑞] 𝑥 = 𝜒𝐹cos(𝜔𝑡)
ou
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [𝑐 𝑒𝑞] 𝑥̇ + [𝑘 𝑒𝑞] 𝑥 = 𝜒𝐹sin(𝜔𝑡)
• Resposta Permanente do Sistema
𝑥 𝑝( 𝑡) = 𝑋( 𝜔) ⋅ cos(𝜔𝑡 − 𝜑)
𝑥 𝑝( 𝑡) = 𝑋( 𝜔) ⋅ sin(𝜔𝑡 − 𝜑)
𝑋(𝜔) = 𝑋𝑠 ⋅ 𝜇
𝜑 = tan−1
(
2𝜉𝛽
1−𝛽2
)
𝑋𝑠 =
𝐹𝑒𝑞
𝑘 𝑒𝑞
; 𝐹𝑒𝑞 = 𝜒𝐹
𝜇 =
1
√(1−𝛽2)2+(2𝜉𝛽)2
;
𝛽 =
𝜔
𝜔 𝑛
• Valores Críticos – Válidos para 𝜉 ≤
√2
2
𝛽| 𝜇 𝑚𝑎𝑥
= √1 − 2𝜉2
𝜇 𝑚𝑎𝑥 =
1
2𝜉√1−𝜉2
𝜔𝑟 = 𝜔 𝑛 √1 − 2𝜉2
𝑋 𝑚𝑎𝑥 = 𝑋𝑠 ⋅ 𝜇 𝑚𝑎𝑥
𝛽| 𝜇=1 = √2 − 4𝜉2
Objetivo (Sistema):
Diminuição da amplitude da resposta de
modo a diminuir:
- os problemas de desgaste e fadiga do
componente mecânico
- precisão dimensional
Solução (sem alterar resposta estática – μ ):
- 𝜔 ↑ (Ex: aumentar velocidade avião)
- 𝜉 ↑ ⇔ 𝑐 ↑
Origem Forças Harmônicas:
- Forças devido à ação das
ondas em plataformas
marítimas
- Forças em prensas
hidráulicas
- Forças de arrasto em asas
de aviões
Nota: 𝜇| 𝜉=0
=
1
|1−𝛽2|
Análise válida para Sistemas Não
Amortecidos ou Sub-amortecidos

17. 17
Objetivo (Apoios):
- Isolamento de fontes de vibração
(equipamentos rotativos)
- Durabilidade dos apoios de fontes de
vibração (fundações de plataformas
marítimas, uniões das asas dos aviões à
fuselagem)
-
• Força Transmitida por uma ligação mola-amortecedor:
𝑓𝑇 = 𝑘𝑥 𝐴 + 𝑐𝑥̇ 𝐴 = 𝐹 𝑇 𝐴
cos( 𝜔𝑡 − 𝜑 + 𝛾)
𝐹 𝑇 𝐴
= √𝑘2 + ( 𝑐𝜔)2 ⋅ 𝑋𝐴( 𝜔) = √𝑘2 + ( 𝑐𝜔)2 ⋅ 𝜆 𝑋( 𝜔)
= 𝜆√ 𝑘
2
+ ( 𝑐𝜔)2 ⋅
𝐹 𝑒𝑞
𝐾 𝑒𝑞
⋅ 𝜇
𝛾 = tan−1 (
𝑐𝜔
𝑘
)
• Transmissibilidade de Força
𝑇𝑅 =
𝐹𝑇 𝐴
𝐹
razão entre a amplitude da força transmitida pela
igação A (𝐹 𝑇) e a amplitude da força de solicitação ( ≠ 𝐹𝑒𝑞 )
Nota: Sempre que num apoio esteja inserido um amortecedor, a
Transmissibilidade de força TR é deteriorada pela força de
amortecimento a partir de certos valores de 𝛽 ( 𝐹𝑐 = 𝑐𝑥̇( 𝑡) )
𝑇𝑅 =
𝜆√𝑘2+(𝑐𝜔)2 𝑋(𝜔)
𝐹
=
𝐹 𝑒𝑞
𝐹
⋅
𝜆√𝑘2+(𝑐𝜔)2
𝐾𝑒𝑞
⋅ 𝜇
Diminuição da Transmissibilidade de Força:
- 𝜔 𝑛 ↓
- 𝜉 𝑚𝑖𝑛 para evitar picos elevados
na transição pela frequência de
ressonância (contudo com efeito
prejudicial para 𝛽 ≥ √2 )
Redução da Transmissibilidade/vibrações
ou Eficiência do Isolamento ( R ):
𝑇𝑅 = 1 − 𝑅

18. 18
1.4.2 - Solicitação Harmónica Ativa – Rotação de Massas em Desiquilibrio
• Resposta Permanente do Sistema
𝑥 𝑝( 𝑡) = 𝑋(𝜔) ⋅ sin(𝜔𝑡 − 𝜑)
𝑋(𝜔) = 𝑋𝑠 ⋅ 𝜇 𝑟𝑜𝑡
𝜑 = tan−1
(
2𝜉𝛽
1−𝛽2
)
𝑋𝑠 = 𝜒
𝑒 𝑚 𝑜
𝑚 𝑒𝑞
;
𝜇 𝑟𝑜𝑡 =
𝛽2
√(1−𝛽2)2+(2𝜉𝛽)2
𝛽 =
𝜔
𝜔 𝑛
• Valores Críticos – Válido para 𝜉 ≤
√2
2
𝛽| 𝜇 𝑚𝑎𝑥
=
1
√1−2𝜉2
𝜇 𝑚𝑎𝑥 =
1
2𝜉√1−𝜉2
(o valor do pico efetivo não se altera,
apenas muda a sua posição)
𝜔 𝑟 =
𝜔 𝑛
√1−2𝜉2
𝑋 𝑚𝑎𝑥 = 𝑋𝑠 ⋅ 𝜇 𝑚𝑎𝑥
Curiosidade: 𝜇 𝑟𝑜𝑡 = 𝜇 ⋅
𝑚 𝑒𝑞 𝜔2
𝑘 𝑒𝑞
𝑓𝑒( 𝑡) = 𝑒 𝑚 𝑜 𝜔2
sin(𝜔𝑡)
𝐹𝑒 = 𝑒 𝑚 𝑜 𝜔2
Nota: 𝜇 𝑟𝑜𝑡 | 𝜉=0
=
𝛽2
|1−𝛽2|

19. 19
1.4.3- Solicitação Harmónica Passiva
• Equação Diferencial do Movimento
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [𝑐 𝑒𝑞] 𝑥̇ + [𝑘 𝑒𝑞] 𝑥 = 𝜒( 𝑘𝑦 + 𝑐𝑦̇)
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [𝑐 𝑒𝑞] 𝑥̇ + [𝑘 𝑒𝑞] 𝑥 = 𝜒√𝑘2 + ( 𝑐𝜔)2 𝑦(𝑡 + 𝛾)
• Resposta Permanente do Sistema
𝑥 𝑝( 𝑡) = 𝑋( 𝜔) ⋅ cos( 𝜔𝑡 − 𝜑 + 𝛾)
𝑥 𝑝( 𝑡) = 𝑋( 𝜔) ⋅ sin( 𝜔𝑡 − 𝜑 + 𝛾 )
𝑋(𝜔) = 𝑋𝑠 ⋅ 𝜇
𝜑 = tan−1
(
2𝜉𝛽
1−𝛽2
)
𝛾 = tan−1
(
𝜔𝑐
𝑘
)
𝑋𝑠 =
𝐹𝑒𝑞
𝑘 𝑒𝑞
; 𝐹𝑒𝑞 = 𝜒 ( 𝑌√𝑘2 + ( 𝜔𝑐)2 )
𝜇 =
1
√(1−𝛽2)2+(2𝜉𝛽)2
Nota: √( 𝑓( 𝑥) )2 = | 𝑓( 𝑥) |
𝛽 =
𝜔
𝜔 𝑛
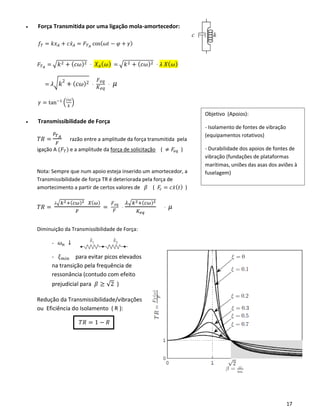
• Força Transmitida por uma ligação mola-amortecedor:
𝑓𝑇 𝐴
= 𝑘𝑥 𝐴 + 𝑐𝑥̇ 𝐴 = 𝐹 𝑇 cos( 𝜔𝑡 − 𝜑 + 𝛾)
𝐹 𝑇 = √𝑘2 + ( 𝜔𝑐)2 𝑋𝐴( 𝜔) = 𝜆√𝑘2 + ( 𝜔𝑐)2 𝑋( 𝜔) =
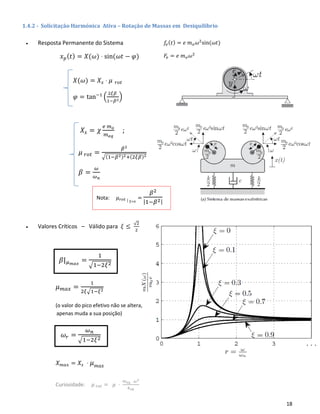
• Transmissibilidade de Deslocamentos:
𝑇𝑅 𝑎𝑏𝑠 =
𝑋 𝐴(𝜔)
𝑌
=
𝜆𝑋(𝜔)
𝑌
= =
𝜆
𝑌
⋅
Feq
𝑘 𝑒𝑞
𝜇 =
𝜆
𝑌
𝜒 ( 𝑌√𝑘2+(𝜔𝑐)2 )
𝑘 𝑒𝑞
𝜇 =
𝜆 𝜒 ( 𝑌√𝑘2+(𝜔𝑐)2 )
𝑘 𝑒𝑞
𝜇
Origem dos Deslocamentos
Harmónicos Impostos:
- Vibrações devido à atividade
sísmica
- Vibração de veiculos devido a
imperfeiçoes do terreno
- Vibrações das bases/apoios
devido a outros sistemas
𝑦( 𝑡) = 𝑌 cos(𝜔𝑡)
𝑦( 𝑡) = 𝑌 sin(𝜔𝑡)
Zona de
Isolamento

20. 20
Zona de
Isolamento
1.4.4- Isolamento de Vibrações
Objetivo do isolamento :
• Atendendo ao conceito de Transmissibilidade (de
força ou deslocamento) com o isolamento
pretende-se 𝛽 ↑ (Zona de Isolamento)
• Admita-se que as condições de funcionamento (
ω ) estão definidas. A única maneira de 𝛽 ↑ é
𝜔 𝑛 ↓
Princípio base do Isolamento de Vibrações – A Transmissibilidade de força é formalmente idêntica à
Transmissibilidade de Deslocamento (Absoluta). Conclui-se assim que é igual o :
• Isolamento da Fonte (source isolation) – Isolamento de Vibração de um sistema
dinâmico sujeito a Transmissão Ativa
Ex: Equipamento vibratório transmite vibrações aos seus apoios
Pensa mecânica, Máquina Ferramenta, Moinho rotativo, Veios de
turbinas e ventiladores
• Isolamento do Receptor (receiver isolation) – Isolamento de um sistema sujeito a vibrações por
Transmissão Passiva
Ex: Meio envolvente (caminhões na estrada próxima, pessoas a andar no
edifício, sismos, obras na estrada, etc..) introduz pequenas vibrações nos
equipamentos geralmente delicados/sensíveis ao ruído
Roda automóvel, mesas de ensaios de laboratórios, pontes, edifícios
(pouco usado), etc..
Técnicas de Isolamento de Vibrações (Considerando ξ =0 para simplificação):
• Bloco de Isolamento
𝑚 𝑒𝑞 ↑↑
Apenas adequado para sistemas ligeiros - para que a massa dos apoios
nao seja desprezável (Ex: Aparelhagem de medição...)
Ex: Mesas de Aparelhagem laboratorial, Prensas e Máquinas Ferramenta
pesadas
𝑅 = 1 − 𝑇𝑅 ⇒ 𝜔 𝑛
2
= 𝜔 2 1−𝑅
2−𝑅
⇒ 𝑚 𝑒𝑞 =
𝑘
𝜔2
2−𝑅
1−𝑅

21. 21
• Plataforma de Isolamento
𝑘 ↓↓
Adequado para sistemas de elevado atravancamento (Ex: pontes,
automóveis...)
Deflecção Estática do próprio sistema 𝑋𝑆 ↑↑ (arranque)
Ex: Placas Elastoméricas, bases de moals helicoidais, bases de ar
comprimido (apresenta algum amortecimento natural)
𝑅 = 1 − 𝑇𝑅 ⇒ 𝜔 𝑛
2
= 𝜔 2 1−𝑅
2−𝑅
⇒ 𝑘 𝑒𝑞 = 𝑚 𝜔2 1−𝑅
2−𝑅
Equivalência da Transmissibilidade de Força ( 𝑇𝑅 ) e Transmissibilidade de deslocamento absoluto ( 𝑇𝑅 𝑎𝑏𝑠 ) :
𝑇𝑅𝑓𝑜𝑟ç𝑎 =
𝐹 𝑇
𝐹
=
𝑘 𝑚𝑜𝑙𝑎 𝑋(𝜔)
𝐹
=
𝑘 𝑚𝑜𝑙𝑎 𝐹𝑒𝑞
𝐹 𝑘 𝑒𝑞
𝜇 = 𝜇 =
1
|1−𝛽2|
=
1
𝛽2−1
=
1
𝜔2
𝜔 𝑛
2−1
𝑇𝑅 𝑎𝑏𝑠 =
𝑋(𝜔)
𝑌
=
𝐹𝑒𝑞
𝑌 𝑘 𝑒𝑞
𝜇 =
𝑘 𝑌
𝑌 𝑘 𝑒𝑞
𝜇 = 𝜇 =
1
|1−𝛽2|
=
1
𝛽2−1
𝑅 = 1 − 𝑇𝑅 = 1 −
1
𝜔 2
𝜔 𝑛
2−1
⇔
𝜔 2
𝜔 𝑛
2 − 1 =
1
1−𝑅
⇔
𝜔 2
𝜔 𝑛
2 =
2−𝑅
1−𝑅
⇔ 𝜔 𝑛
2
= 𝜔 2 1−𝑅
2−𝑅

22. 22
Conceitos Derivados EXCLUSIVAMENTE para o
sistema representado
1.4.5- Transdutor de Vibrações
Definição: Instrumento que converte variações de
grandezas físicas em variações de sinal elétrico. Por
outras palavras, converte energia mecânica em energia
elétrica.
Tipos de Transdutores (modelo de funcionamento):
• Transdutor Sísmico – Modelo mecânico
massa-mola-amortecedor;
• Transdutor piezoelétrico – Trandutores que
recorrem a cristais piezoelétricos que produzem
carga elétrica quando sujeitados a tensões de
corte, comrpessão e tração;
Banda / Faixa útil de frequência – Gama de frequências para a qual a resposta/saída do transdutor é
relativamente independente das compenentes de frequência presentes no fenómeno dinâmico a ser
medido.
Tipos de Transdutores (banda útil):
• Vibrómetros:
o Transdutores de posição/deslocamento
o com 𝜔 𝑛 ↓ (massa ↑ e rigidez ↓)
o Adequados para medição de 𝜔 ↑ ( 𝜔 > 3 𝜔 𝑛 ) e sistemas pouco sensíveis à introdução do
vibrómetro
( Ex: Vibração nos solos )
o Velocidade e Aceleração obtidos por derivação
• Acelerómetros :
o Transdutores de aceleração
o com 𝜔 𝑛 ↑ (massa ↓ e rigidez ↑)
o Adequados para a medição de 𝜔 ↓ e
sistemas ligeiros
( Ex: Maioria dos Sistemas Mecânicos )
o Velocidade e Posição obtidos por integração
𝑇𝑅𝑟𝑒𝑙=
𝑍(𝜔)
𝑌
=𝜇𝑟𝑜𝑡

23. 23
Aceleração Teórica do
Sistema
𝑦( 𝑡) = 𝑌 sin(𝜔𝑡)
𝑦̈( 𝑡) = −𝑌𝜔2
sin(𝜔𝑡)
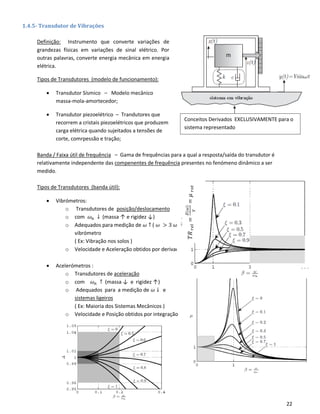
Estudo do Transdutor Sísmico
• O transdutor Sísmico apenas regista o movimento relativo 𝑧(𝑡) (entre a régua graduada da caixa, e o
apontador da massa)
• Equação Diferencial de Movimento
[ 𝑚 ] 𝑥̈ + [ 𝑐] 𝑥̇ + [ 𝑘] 𝑥 = 𝑘𝑦 + 𝑐𝑦̇
𝑚𝑥̈ + 𝑐𝑥̇ − 𝑐𝑦̇ + 𝑘𝑥 − 𝑘𝑦 = 0 ; 𝑧(𝑡) = 𝑥(𝑥) − 𝑦(𝑡)
𝑚 𝑧̈ + 𝑐 𝑧̇ + 𝑘𝑧 = −𝑚𝑦̈ = 𝑚𝜔2
𝑦 , 𝐹𝑒𝑞 = 𝑌𝑚𝜔2
𝑧( 𝑡) = 𝑍( 𝜔) sin( 𝜔𝑡 − 𝜑) ; 𝑍( 𝜔) =
𝐹𝑒𝑞
𝑘
𝜇 =
𝑌𝑚𝜔2
𝑘
𝜇 = 𝑌𝜇 𝑟𝑜𝑡
Dimensionamento de Vibrómetros - Transmissibilidade Relativa
𝑇𝑅 𝑟𝑒𝑙 =
𝑍(𝜔)
𝑌
=
𝑌 𝜇 𝑟𝑜𝑡
𝑌
= 𝜇 𝑟𝑜𝑡
Para que 𝑍( 𝜔) = 𝑌(𝜔)
é necessário que 𝑇𝑅 𝑟𝑒𝑙 = 𝜇 𝑟𝑜𝑡
= 1
Erro Medição (E): 𝐸 = |1 – 𝑇𝑅 𝑟𝑒𝑙|
Dimensionamento de Acelerámetro
Manipulação da Resposta Relativa 𝑧(𝑡)
𝑧( 𝑡) =
𝐹𝑒𝑞
𝑘
𝜇 sin( 𝜔𝑡) =
𝑌𝑚𝜔2
𝑘
𝜇 sin( 𝜔𝑡 − 𝜑)
−𝑧( 𝑡) = −
𝑌𝑚𝜔2
𝑘
𝜇 sin( 𝜔𝑡 − 𝜑)
−𝑧( 𝑡)
𝑘
𝑚
= − 𝜇 𝑌𝜔2
sin( 𝜔𝑡 − 𝜑) ⇔
−𝑧( 𝑡) 𝜔 𝑛
2
= − 𝜇 𝑌𝜔2
sin( 𝜔𝑡 − 𝜑)
◊ É necessário que 𝜇 = 1
◊ Basta medir o deslocamento 𝑧(𝑡) e afeta-lo da constante −𝜔 𝑛
2
e
obtem-se facilmente a aceleração do sistema
Erro Medição (E): 𝐸 = |1 – 𝜇|

24. 24
1.5- Regime Forçado Periódico - Não Harmônico
• Equação Diferencial do Movimento Base:
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [𝑐 𝑒𝑞] 𝑥̇ + [𝑘 𝑒𝑞] 𝑥 = 𝜒 𝑓( 𝑡)
• Modelação da Excitação ( Expansão de 𝑓(𝑡) pela serie de Fourier: )
𝑓( 𝑡) =
𝐹0
2
+ ∑ 𝐹𝑝cos(𝑝𝜔𝑡 − 𝛾𝑝)∞
𝑝=1 expressão ja agrupada
𝐹0 = 𝑣𝑎𝑙𝑜𝑟 𝑚é𝑑𝑖𝑜 =
2
𝑇
∫ 𝑓( 𝑡) 𝑑𝑡
𝑇
0
𝐹𝑝 = √𝐴 𝑝
2
+ 𝐵𝑝
2
𝛾𝑝 = tan−1
(
𝐵 𝑝
𝐴 𝑝
)
𝐴 𝑝 =
2
𝑇
∫ 𝑓( 𝑡)∗
⋅ cos( 𝑝𝜔𝑡) 𝑑𝑡
𝑇
0
em que 𝜔 =
2𝜋
𝑇
𝐵𝑝 =
2
𝑇
∫ 𝑓( 𝑡)∗
⋅ sin( 𝑝𝜔𝑡) 𝑑𝑡
𝑇
0
T – periodo da solicitação periódica
• Resposta Permanente do Sistema
𝑥 𝑝( 𝑡) =
𝐹0
2𝐾𝑒𝑞
+ ∑ 𝑋 𝑝(𝜔) ⋅ cos(𝑝𝜔𝑡 − 𝜑 𝑝 − 𝛾𝑝)∞
𝑝=1
𝑋 𝑝(𝑝𝜔) = 𝑋𝑠𝑝 𝜇 𝑝 𝑋𝑠𝑝 =
𝐹𝑝
𝑘 𝑒𝑞
𝜇 𝑝 =
1
√(1−𝛽 𝑝)
2
−(2𝜉𝛽 𝑝)
2
𝛽 𝑝 = 𝑝𝜔/𝜔 𝑛
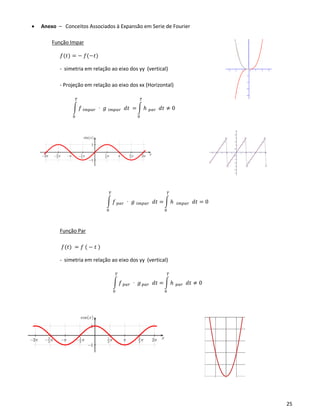
• Critério de Truncatura da Série:
Paridade de 𝑓( 𝑡)
/ par impar
𝐴 𝑝 - 0
𝐵𝑝 0 -
𝛾𝑝
0
𝑘
= 0
0
−𝑘
= 𝜋
𝑘
0
=
𝜋
2
−𝑘
0
= −
𝜋
2
Relação 𝝎 𝒓 ∞ 𝝎 Truncatura (p)
𝜔 ≪ 𝜔𝑟 ∈ [1, 𝑝 =
𝜔𝑟
𝜔
+ 𝜀]
𝜔 ≈ 𝜔𝑟 ou 𝜔 ≫ 𝜔𝑟 ∈ [1, 1 + 𝜀]
Resolução na máquina (não é CaseSensitie):
𝐴 𝑝 =
2
𝑎
∫ 𝑓( 𝑡) ⋅ cos (𝑝
2𝑟
𝑎
𝑡) 𝑑𝑡
𝑎
0
𝐵𝑝 =
2
𝑎
∫ 𝑓( 𝑡) ⋅ sin (𝑝
2𝑟
𝑎
𝑡) 𝑑𝑡
𝑎
0

25. 25
• Anexo – Conceitos Associados à Expansão em Serie de Fourier
Função Impar
𝑓(𝑡) = − 𝑓(−𝑡)
- simetria em relação ao eixo dos yy (vertical)
- Projeção em relação ao eixo dos xx (Horizontal)
∫ 𝑓 𝑖𝑚𝑝𝑎𝑟 ⋅ 𝑔 𝑖𝑚𝑝𝑎𝑟 𝑑𝑡 =
𝑇
0
∫ ℎ 𝑝𝑎𝑟 𝑑𝑡 ≠ 0
𝑇
0
∫ 𝑓 𝑝𝑎𝑟 ⋅ 𝑔 𝑖𝑚𝑝𝑎𝑟 𝑑𝑡 =
𝑇
0
∫ ℎ 𝑖𝑚𝑝𝑎𝑟 𝑑𝑡 = 0
𝑇
0
Função Par
𝑓(𝑡) = 𝑓 ( − 𝑡 )
- simetria em relação ao eixo dos yy (vertical)
∫ 𝑓 𝑝𝑎𝑟 ⋅ 𝑔 𝑝𝑎𝑟 𝑑𝑡 =
𝑇
0
∫ ℎ 𝑝𝑎𝑟 𝑑𝑡 ≠ 0
𝑇
0

26. 26
1.6- Regime Forçado Não Periódico (Impulsiva e transiente)
1.7.1- Regime Forçado Impulsivo
• Equação Diferencial do Movimento Base:
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [𝑐 𝑒𝑞] 𝑥̇ + [𝑘 𝑒𝑞] 𝑥 = 𝑓( 𝑡) = 𝐹̃ 𝛿( 𝑡 − 𝜏)
Teorema do Impulso e Q.M: 𝐹̌ = ∫ 𝑓( 𝑡) 𝑑𝑡
𝑡+𝛥𝑡
𝑡
= 𝛥𝑄 = 𝑚𝛥𝑥̇
Função Impulso Unitário: 1 = ∫ 𝛿(𝑡 − 𝜏)𝑑𝑡
+∞
−∞
Definição alternativa de força impulsiva: 𝑓( 𝑡) = 𝐹̌ 𝛿(𝑡 − 𝜏)
Função Resposta Impulsiva: ℎ( 𝑡 − 𝜏) =
1
𝑚𝜔 𝑑
𝑒−𝜉𝜔 𝑛 (𝑡−𝜏)
sin [𝜔 𝑑 ( 𝑡 − 𝜏)]
• Resposta total a uma força impulsiva - 𝑥(𝑡)
𝑥( 𝑡) = {
𝐴𝑒−𝜉𝜔 𝑛 𝑡
𝑐𝑜𝑠(𝜔 𝑑 𝑡 − 𝜑), 𝑡 > 0
𝐹̃
𝑚𝜔 𝑑
𝑒−𝜉𝜔 𝑛 (𝑡−𝜏)
sin [ 𝜔 𝑑 ( 𝑡 − 𝜏̅)] , 𝑡 ≥ 𝜏̅
𝜏̅ − 𝑖𝑛𝑠𝑡𝑎𝑛𝑡𝑒 𝑑𝑒 𝑎𝑡𝑢𝑎çã𝑜 𝑑𝑜 𝑖𝑚𝑝𝑢𝑙𝑠𝑜 (𝑣𝑎𝑙𝑜𝑟 𝑓𝑖𝑛𝑖𝑡𝑜, 𝑛ã𝑜 é 𝑣𝑎𝑟𝑖á𝑣𝑒𝑙!)
1.7.2- Regime Forçado Transiente
• Equação Diferencial do Movimento Base:
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [𝑐 𝑒𝑞] 𝑥̇ + [𝑘 𝑒𝑞] 𝑥 = 𝑓( 𝑡) = ∫ 𝑓( 𝜏) 𝑑𝜏
𝑡 𝑐
0
• Modelação da Excitação
Modelação do sinal
de excitação tendo o zero
como origem do referencial
(referência τ inicial). No final afetar f (τ
– τ) e introduzir a informação de
desfasamento na atuação de f nos
limites de integração
Análise válida para Sistemas:
• Não Amortecidos
• Sub-amortecidos

27. 27
• Resposta total do sistema
𝑥( 𝑡) =
{
𝐴𝑒−𝜉𝜔 𝑛 𝑡 𝑐𝑜𝑠( 𝜔 𝑑 𝑡 − 𝜑) , 𝑡 > 0
1
𝑚 𝑒𝑞 𝜔 𝑑
⋅ [ ∫ f(τ − 𝜏) ⋅ e−𝜉𝜔 𝑛 (𝑡−𝜏)
⋅ sin[ 𝜔 𝑑( 𝑡 − 𝜏)] 𝑑𝜏
𝑡
𝜏
] , 𝜏̅ < 𝑡 < 𝑡 𝑐
1
𝑚 𝑒𝑞 𝜔 𝑑
⋅ [ ∫ f(τ − 𝜏) ⋅ e−𝜉𝜔 𝑛 (𝑡−𝜏)
⋅ sin[ 𝜔 𝑑( 𝑡 − 𝜏)] 𝑑𝜏
𝑡 𝑐
𝜏
] , 𝑡 > 𝑡 𝑐
Em que: 𝜏 − instante de aplicação da força impulsiva transiente
𝜏 − variável tempo que descreve a atuação da força impulsiva,variável de integração
𝑡 − variável tempo que descreve de forma geral a resposta do sistema,associada precisamente
à resposta do sistema,nunca é integrada
𝑡 𝑐 − intanste em que finda a aplicação da força transiente

28. 28
2 - Graus de Liberdade
2.1- Glossário
• Coordenadas Generalizadas – coordenadas independentes necessárias para descrever integralmente a
cinemática do sistema (𝑞𝑖) ( descrever a posição de cada componente do sistema em qualquer instante).
As unidades das coordenadas não são necessariamente comprimentos ou angulos, e são independentes
das ligações às massas concentradas.
• Coordenadas Naturais, Modais ou Principais – Coordenadadas generalizadas para as quais não há
acoplamenteo de inércia, rigidez ( este acoplamento é função apenas das coordenadas generalziadas
selecionadas). As coordenadas naturais designam-se também por coeficientes de participação das formas
naturais e resultam da projecção das C.G na base modal.
• Equação Diferencial do Movimento – Para um sistema com n G.L. e EDM consiste num Sistema de
Equações Diferenciais lineares ordinárias não homogêneas, dependentes entre si.
• Hipótese de Resolução – O primeiro passo para resolver uma equação diferencial homogenia (EDM em
regime livre) é determinar uma solução particular, para por combinação linear das soluções particulares,
obter uma solução geral da eqação. Para obter o conjunto de soluções particulares admite-se: “movimento
harmônico síncrono sem desfazamento entre as masssas, à frequência natural”. As soluções que
verifiquem esta condição correspondem a soluções particulares da equação.
• Problema Característico - Resulta de admitir um movimento harmônico síncrono e sem desfazamento
para as massas concentradas (hipótese de resolução). Problema de valores característicos e vetores
característicos (vetores modais). O problema característico compreende o determinante característico e a
Equação característica.
EDM
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [ 𝑘 𝑒𝑞 ] 𝑥 = 0
A solução é da forma | 𝑥( 𝑡)| 𝑖 = | 𝑢|𝑖 cos( 𝜔𝑖 𝑡 − 𝜑) (Resulta da Hipótese de resolução)
[ 𝑚 𝑒𝑞 ] − 𝜔2| 𝑢𝑖| cos( 𝜔𝑖 𝑡 − 𝜑) + [ 𝑘 𝑒𝑞 ] | 𝑢𝑖|cos( 𝜔𝑖 𝑡 − 𝜑) = 0
(−𝜔2[ 𝑚 𝑒𝑞 ] + [ 𝑘 𝑒𝑞 ]) | 𝑢𝑖| cos( 𝜔𝑖 𝑡 − 𝜑) = 0
Problema Característico - Para que a eq anterior seja válida para qualquer t, temos que:
(−𝜔2[ 𝑚 𝑒𝑞 ] + [ 𝑘 𝑒𝑞 ]) | 𝑢𝑖| = 0
Determinante Característico
det( −𝜔2[ 𝑚 𝑒𝑞 ] + [ 𝑘 𝑒𝑞 ] )
Equação Característica ou de Frequências
det( −𝜔2[ 𝑚 𝑒𝑞 ] + [ 𝑘 𝑒𝑞 ] ) = 0
Nota: Problema de valores e vetores
próprios consiste, na pratica, num sistema
com 2 variáveis (valroes e vetores) e com
2 formas de resolução

29. 29
• Modos Naturais de Vibração
- Soluções particulares, não triviais da EDM, para as quais o movimento harmônico síncrono é possível
- Definidos por um par característico ( 𝜔𝑖 ; | 𝑢|𝑖 ), obtidos a partir das soluções do Problema Caract.
- Fisicamente representam os movimentos oscilatórios em torno da posição de equilibbrio, que as
massas concentradas executam, todas com a mesma frequência natural, em regime livre com
movimento harmônico síncrono.
- Propriedade intrínseca do sistema, função das propriedades mecânicas do sistema
- Ortogonais entre si, isto é, são independentes entre si, não podendo ser obtidos por combinação
linear dos restantes modos.
Definidos por | 𝑥( 𝑡)|𝑖 = | 𝑢|𝑖 cos( 𝜔𝑖 𝑡 − 𝜑𝑖)
• Vetores Modais |u|
- Soluções não triviais do Problema característico associadas a uma frequência natural 𝜔𝑖 .
- Representam as formas naturais de vibração, isto é, definem as configurações espaciais
assumidas pelo sistema, durante o movimento síncrono em regime livre ou natural
(às frequencias naturais 𝜔1 e 𝜔2 )
- Representam as relações de amplitudes do movimento harmônico síncrono, em regime livre, das
massas concentradas do sistema, às frequências naturais.
- Consiste na representação física dos deslocamentos relativos entre os pontos das
massas concentradas a uma determinada frequência natural.
Definidos por | 𝑢|𝑖 = |
1
𝑟𝑖
|
• Frequências Naturais
– Soluções não triviais da Equação característica.
– Consistem nas frequências para as o movimento harmônico síncrono do sistema é possível .
– Valores próprios 𝜔2
do Problema característico, para os quais os vetores próprios | 𝑢|𝑖 admitem
solução não nula
• Nodo de Vibração – Ponto do elemento elástico que liga duas massas concentradas que permanece
estacionário ao longo do movimento harmônico em regime livre ou natural

30. 30
• Anexo de Demonstrações relativas ao Problema Característico
- Colocar na forma de problema de Vetores e Valores prórpios:
[ 𝑘 𝑒𝑞 ] | 𝑢𝑖| = 𝜔2[ 𝑚 𝑒𝑞 ] | 𝑢𝑖| ⇒ [ 𝑚 𝑒𝑞 ]
−1
[ 𝑘 𝑒𝑞 ] | 𝑢𝑖| = 𝜔2[ 𝑚 𝑒𝑞 ]
−1
[ 𝑚 𝑒𝑞 ] | 𝑢𝑖|
[ 𝑚 𝑒𝑞 ]
−1
[ 𝑘 𝑒𝑞 ] | 𝑢𝑖| = 𝜔2 | 𝑢𝑖| ⇒ [𝐴] | 𝑢𝑖| = 𝜔2| 𝑢𝑖|
- Justificação da necessidade de determinante nulo:
[𝐴] | 𝑣| = 𝜆| 𝑣| ⇒ [
𝑎11 𝑎12
𝑎21 𝑎22
] |
𝑣1
𝑣2
| = |
𝜆𝑣1
𝜆𝑣2
| ⇒ {
𝑎11 𝑣1 + 𝑎12 𝑣2 = 𝜆𝑣1
𝑎12 𝑣1 + 𝑎22 𝑣2 = 𝜆𝑣2
{
𝑣1 =
𝑎12
𝜆−𝑎11
𝑣2
𝑣1 =
𝜆−𝑎22
𝑎12
𝑣2
⇒
𝑎11
𝜆−𝑎11
𝑣1 =
𝜆−𝑎22
𝑎12
𝑣1 ⇒ 𝑎11 𝑎12 = ( 𝜆 − 𝑎22)( 𝜆 − 𝑎11) c.q.d.
det( [𝐴] − 𝜆[𝐼]) = 0 ⇒ det ( [
𝑎11 − 𝜆 𝑎12
𝑎21 𝑎22 − 𝜆
] ) = 0
( 𝑎11 − 𝜆)( 𝑎22 − 𝜆) − 𝑎11 𝑎22 = 0 ⇒ ( 𝑎11 − 𝜆)( 𝑎22 − 𝜆) = 𝑎11 𝑎22 c.q.d.
- Teorema da Algebra Linear: Seja um sistema linear algébrico homogenio, para se obter soluções não
nulas e necessário que o determinante da matriz dos coeficientes seja nulo. Este teorema define que
qualquer sistema algebrico homogenio pode ser expresso na forma de um problema de vetores e valroes
próprios, . Aplicação na determinação de frequencias naturais de sistemas continuos!
• Anexo – Propriedades das Matrizes
o Transposta
( 𝐴 𝑇) 𝑇
= 𝐴
( 𝑐𝐴) 𝑇
= 𝑐𝐴 𝑇
( 𝐴𝐵) 𝑇
= 𝐵 𝑇
𝐴 𝑇
( 𝐴𝐵𝐶) 𝑇
= 𝐶 𝑇
𝐵 𝑇
𝐴 𝑇
o Simétrica
𝐴 𝑇
= 𝐴
• Conceitos Vetoriais:
o Vetores ortogonais - | 𝑣𝑖 | 𝑇 | 𝑣𝑗 | = 0
o Vetores normalizados - | 𝑣𝑖 | 𝑇 | 𝑣𝑖 | = 1
o Vetores ortonormais - | 𝑣𝑖 | 𝑇 | 𝑣𝑗 | = {
1 𝑝𝑎𝑟𝑎 𝑖 = 𝑗
0 𝑝𝑎𝑟𝑎 𝑖 ≠ 𝑗
Propriedade importante para
aplicação da técnica de Análise
Modal. A ortogonalidade permite
o desacoplamento das ED do
sistema
Definição de valor e vetor próprio:
[𝐴] | 𝑣| = 𝜆 | 𝑣|

31. 31
• Propriedades dos Vetores Modais:
o Ortogonalidade em relação à massa - | 𝑢𝑖| 𝑇 [𝑚] |𝑢𝑗| = 0
[ 𝑘 𝑒𝑞 ] | 𝑢𝑖| = 𝜔2[ 𝑚 𝑒𝑞 ] | 𝑢𝑖|
[ 𝑘 𝑒𝑞 ] | 𝑢1| = 𝜔1
2
[ 𝑚 𝑒𝑞 ] | 𝑢1| | 𝑢2| 𝑇[ 𝑘 𝑒𝑞 ] | 𝑢1| = 𝜔1
2| 𝑢2| 𝑇[ 𝑚 𝑒𝑞 ] | 𝑢1|
[ 𝑘 𝑒𝑞 ] | 𝑢2| = 𝜔2
2
[ 𝑚 𝑒𝑞 ] | 𝑢2| | 𝑢1| 𝑇[ 𝑘 𝑒𝑞 ] | 𝑢2| = 𝜔2
2| 𝑢1| 𝑇[ 𝑚 𝑒𝑞 ] | 𝑢2|
( | 𝑢2| 𝑇[ 𝑘 𝑒𝑞 ] | 𝑢1| )
𝑇
= ( 𝜔1
2| 𝑢2| 𝑇[ 𝑚 𝑒𝑞 ] | 𝑢1| )
𝑇
| 𝑢1| 𝑇[ 𝑘 𝑒𝑞 ] | 𝑢2| = 𝜔1
2| 𝑢1| 𝑇[ 𝑚 𝑒𝑞 ] | 𝑢2|
| 𝑢1| 𝑇[ 𝑘 𝑒𝑞 ] | 𝑢2| = 𝜔2
2| 𝑢1| 𝑇[ 𝑚 𝑒𝑞 ] | 𝑢2| | 𝑢1| 𝑇[ 𝑘 𝑒𝑞 ] | 𝑢2| = 𝜔2
2| 𝑢1| 𝑇[ 𝑚 𝑒𝑞 ] | 𝑢2|
𝜔1
2| 𝑢1| 𝑇[ 𝑚 𝑒𝑞 ] | 𝑢2| = 𝜔2
2| 𝑢1| 𝑇[ 𝑚 𝑒𝑞 ] | 𝑢2|
| 𝑢1| 𝑇[ 𝑚 𝑒𝑞 ] | 𝑢2|( 𝜔1
2
− 𝜔2
2) = 0 como 𝜔1
2
− 𝜔2
2
≠ 0 , entao
| 𝑢1| 𝑇[ 𝑚 𝑒𝑞 ] | 𝑢2| = 0
o Ortogonalidade em relação à rigidez - | 𝑢𝑖| 𝑇 [𝑘] |𝑢𝑗| = 0
| 𝑢1| 𝑇[ 𝑘 𝑒𝑞 ] | 𝑢2| = 𝜔1
2| 𝑢1| 𝑇[ 𝑚 𝑒𝑞 ] | 𝑢2|
| 𝑢1| 𝑇[ 𝑘 𝑒𝑞 ] | 𝑢2| = 𝜔2
2| 𝑢1| 𝑇[ 𝑚 𝑒𝑞 ] | 𝑢2|
1
𝜔1
2 | 𝑢1| 𝑇[ 𝑘 𝑒𝑞 ] | 𝑢2| =
1
𝜔2
2 | 𝑢1| 𝑇[ 𝑘 𝑒𝑞 ] | 𝑢2| ⇒ | 𝑢1| 𝑇[ 𝑘 𝑒𝑞 ] | 𝑢2| = 0
o Normalização em relação à massa - | 𝜑𝑖| 𝑇 [𝑚] | 𝜑𝑖| = 1
- Ortonormalidade em relação à massa: | 𝜑𝑖| 𝑇 [𝑚] |𝜑𝑗| = {
1 𝑝𝑎𝑟𝑎 𝑖 = 𝑗
0 𝑝𝑎𝑟𝑎 𝑖 ≠ 𝑗
- Ortonormalidade em relação à rigidez: | 𝜑𝑖| 𝑇 [𝑘] |𝜑𝑗| = {
𝜔𝑖
2
𝑝𝑎𝑟𝑎 𝑖 = 𝑗
0 𝑝𝑎𝑟𝑎 𝑖 ≠ 𝑗
[ 𝑘 𝑒𝑞 ] | 𝜑𝑖| = 𝜔2[ 𝑚 𝑒𝑞 ] | 𝜑𝑖| | 𝜑𝑖| 𝑇[ 𝑘 𝑒𝑞 ] | 𝜑𝑖| = 𝜔2| 𝜑𝑖| 𝑇[ 𝑚 𝑒𝑞 ] | 𝜑𝑖|
mas | 𝜑𝑖| 𝑇[ 𝑚 𝑒𝑞 ] | 𝜑𝑖| = 1 logo | 𝜑𝑖| 𝑇[ 𝑘 𝑒𝑞 ] | 𝜑𝑖| = 𝜔2
Significado físico da propriedade de ortonormalidade: Fisicamente representa a independência
entre os vetores modais. Por outras palvaras, representa o facto de os vetores modais não
poderem ser obtidos por combinação linear de outros vetores modais . Define o facto de o sistema
poder evoluir e n formas independentes e distintas quando devidamente excitado.

32. 32
• Solicitação de um modo natural específico
Aplicação das Condições Iniciais
| 𝑥0| = [𝑈] |
𝑐1 cos( 𝜔1(0) − 𝜑1)
𝑐2 cos( 𝜔2(0) − 𝜑2)
| ; com [𝑈] = [
1 1
𝑟1 𝑟2
]
| 𝑥̇0| = [𝑈] |
−𝑐1 𝜔1 sin( 𝜔1(0) − 𝜑1)
−𝑐2 𝜔2 sin( 𝜔2(0) − 𝜑2)
|
Obtem-se assim o sistema de Equações
𝑥0
1
= 𝑐1 𝑐𝑜𝑠(−𝜑1) + 𝑐2 𝑐𝑜𝑠(−𝜑2)
𝑥0
1
= 𝑐1 𝑟1 𝑐𝑜𝑠(−𝜑1) + 𝑐2 𝑟2 𝑐𝑜𝑠(−𝜑2)
𝑥0
1
= −𝑐1 𝜔1 𝑠𝑖𝑛(−𝜑1) + −𝑐2 𝜔2 𝑠𝑖𝑛(−𝜑2)
𝑥0
1
= −𝑐1 𝜔1 𝑟1 𝑠𝑖𝑛(−𝜑1) + −𝑐2 𝜔2 𝑟2 𝑠𝑖𝑛(−𝜑2)
Solicitação do 1º modo natural:
𝑐1 = 1 𝑒 𝑐2 = 0
𝜑1 = 0 𝑒 𝜑2 = 𝑞𝑢𝑎𝑙𝑞𝑢𝑒𝑟
Solicitação do 2º Modo Natural:
𝑐1 = 0 𝑒 𝑐2 = 1
𝜑1 = 𝑞𝑢𝑎𝑙𝑞𝑢𝑒𝑟 𝑒 𝜑2 = 0
• Frequência natural nula
– Sistemas Semi-definidos (sistemas com um modo natural de corpo rígido, frequencia natural
fundamental é nula ; apresentam ainda um modo elástico de vibração natural)
A resposta em regime livre é dada pela
combinação linear dos modos naturais
Resposta na forma:
| 𝑥( 𝑡) | = [ 𝑈 ] |
𝑐1 cos( 𝜔1 𝑡 − 𝜑1)
𝑐2 cos( 𝜔2 𝑡 − 𝜑2)
|
𝑥0
1
= 𝑐1 cos( 𝜑1) + 𝑐2 cos( 𝜑2)
𝑥0
1
= 𝑐1 𝑟1 cos( 𝜑1) + 𝑐2 𝑟2 cos( 𝜑2)
𝑥0
1
= 𝑐1 𝜔1 sin( 𝜑1) + 𝑐2 𝜔2 sin( 𝜑2)
𝑥0
1
= 𝑐1 𝜔1 𝑟1 sin( 𝜑1) + 𝑐2 𝜔2 𝑟2 sin( 𝜑2)
𝑥0
1
= 1
𝑥0
1
= 𝑟1
𝑥0
1
= 0
𝑥0
1
= 0
𝑥0
1
= 1
𝑥0
1
= 𝑟2
𝑥0
1
= 0
𝑥0
1
= 0

33. 33
• Coeficientes de Influência – Termos das matrizes de:
– Rigidez:
Obtidos pela resolução de n sistema de n equações, de equilibrio estático para o calculo das:
forças 𝑓𝑖 = 𝑘𝑖𝑗 resultantes da aplicação de um deslocamento unitário 𝑑𝑗 e impondo-se deslocamento
nulos para os restantes pontos
𝑘𝑖𝑗 força provocada em 𝑖 devido a um deslocamento unitário em 𝑗, impondo-se 𝑑𝑙 = 0 para 𝑙 ≠ 𝑗
– Flexibilidade:
Obtidos pela resolução de n equações, de equilibrio estático para o calculo das:
deslocamentos 𝛼𝑖𝑗 resultantes da aplicação de uma força unitário 𝑓𝑗 sendo nula as forças nos restnates
pontos
𝛼𝑖𝑗 deslocamento em 𝑖 devido à aplicação de uma força unitária em 𝑗, com 𝑓𝑙 = 0 para 𝑙 ≠ 𝑗
– Inércia
Obtidos pelo resolução de n equações do principio do impulso e da quantidade de movimento, para o
calculo dos impulso 𝐼𝑖 = 𝑚𝑖𝑗 necessários para produzir uma velocidade unitária 𝑥̇ 𝑖 e nula para 𝑙 ≠ 𝑗
𝑚𝑖𝑗 impulso necessário em 𝑖 para produzir uma velocidade instantanea unitária em j, com velocidade
nula 𝑥̇ 𝑙 = 0 para 𝑙 ≠ 𝑗
• Caracterizar as Energias Cinética e Potencial
– Por defnição de 𝐸𝑐 =
𝑚
2
𝑥̇2
, logo a energia cinética associada a um sistema com n G.L. será da forma
𝑇 = ∑ 𝑇𝑖
𝑛
𝑖 = ∑
𝑚 𝑖
2
𝑥̇ 𝑖
2𝑛
𝑖 na forma matricial 𝑇 = | 𝑥̇| 𝑇[𝑚]|𝑥̇|
Em coordenadas generalizadas a energia cinética será função das massas generalizadas e das
velocidades generalizadas 𝑇 = 𝑇𝑖 = ∑ ∑
𝑚 𝑖𝑗
2
𝑞̇ 𝑖𝑗
2𝑛
𝑗
𝑛
𝑖 na forma matricial 𝑇 = | 𝑞̇| 𝑇[𝑚]|𝑞̇|
A energia cinética é então uma função quadrática das velocidades e como é sempre positiva (apenas
será nula na situação estática) designa-se por forma Quadrática Definida Positiva. Tal como
evidenciado na notação matricial, a matriz de inércia ou de massa é simétrica e designa-se por
Matriz Definida Positiva
– Por definição de energia de deformação elástica 𝐸 𝑝 = 𝐹𝑖 𝑥𝑗 e atendendo à definição de força elástica
vem 𝐹𝑖 = 𝑘𝑖𝑗 𝑥𝑗 . Logo a energia potencial elástica pode ser definida por 𝐸 𝑝 = 𝑘𝑖𝑗 𝑥𝑗
2
A energia de deformação elástica associada a um sistema com n G.L. será pois dada por
𝑉 = ∑ 𝑉𝑖
𝑛
𝑖 = ∑ ∑
𝑘 𝑖𝑗
2
𝑥𝑖𝑗
2𝑛
𝑗
𝑛
𝑖 na forma matricial 𝑉 = | 𝑥| 𝑇[𝑘]|𝑥|
A energia potencial é então uma função quadrática dos deslocamentos e é geralmente positiva
(apenas será nula: na situação trivial estática sem carregamento e também em sistemas semi-definidos
sem que todos os deslocamento sejam nulos). Logo designa-se por Forma Quadrática Definid Positiva
(sistemas definidos) ou Forma Quadrática Semi-Definida Positiva (sistemas semi-definidos). Por sua
vez a matriz de inércia ou de massa é simétrica e designa-se por Matriz Definida Positiva
(sistemas definidos) ou uma Matriz Semi-Definida Positiva (sistemas semi-definidos)

34. 34
• Princípio de Hamilton – Formulação Variacional que permite o estabelecimento das EDM. O princípio
afirma que: “Num sistema mecânico, a variação da Energia Cinética mais a variação da Energia Potencial
mais a variação do Trabalho das Forças não conservaticas num intervalo qualquer entre 𝑡1 e 𝑡2 é
necesariamente nula.”
∫ 𝛿( 𝑇 − 𝑉) 𝑑𝑡
𝑡2
𝑡1
+ ∫ 𝛿𝑊𝑓𝑛𝑐
𝑡2
𝑡2
𝑑𝑡 = 0
Instantaneamente Variação
Energia Cinética 𝑇 = ∑ ∑
𝑚𝑖𝑗
2
𝑞̇ 𝑖𝑗
2
𝑛
𝑗
𝑛
𝑖
𝛿𝑇 =
𝜕𝑇
𝜕𝑞𝑖
𝛿𝑞𝑖 +
𝜕𝑇
𝜕𝑞̇ 𝑖
𝛿𝑞̇ 𝑖
Energia
Potencial
𝑉 = ∑ ∑
𝑘𝑖𝑗
2
𝑥𝑖𝑗
2
𝑛
𝑗
𝑛
𝑖
𝛿𝑉 =
𝜕𝑉
𝜕𝑞𝑖
𝛿𝑞𝑖
Trabalho FNC 𝑊𝑓𝑛𝑐 = 𝑄𝑖 𝑞𝑖 𝛿𝑊𝑓𝑛𝑐 = 𝑄𝑖 𝛿𝑞𝑖
• Método da Energia de Rayleigh – Método de determinação aproximada da frequência natural
fundamental de vibração. Assenta no princípio da conservação da Energia mecânica.
o Requisítos dos vetores de aproximação |𝑣| do vetor modal | 𝑢| :
- Vetor não nulo
- Vetor com a dimensão igual ao nº de G.L do sistema
o Propriedades do Quociente de Rayleigh:
- Apresenta um valor estacionário na vizinhança das formas naturais
- Admite um valor estacionário mínimo na vizinhança da frequência natural fundamental
(é um majorante da frequência natural fundamental 𝑅(| 𝑣|) ≥ 𝜔1 )
- Processo Convergente: Se o vetor aproximação diferir de uma pequena quantidade de
1ªordem do vetor modal | 𝑢|𝑖 , então o Quociente de Rayleigh difere de uma quantidade de
2ªordem do quadrado da frequência natural 𝑖 , 𝜔𝑖
2
. A frequência estimada apresenta sempre
menor erro que o vetor aproximação usado
- Quando o vetor de aproximação coincide com o vetor modal para uma dada frequência natural
o quaciente de Rayleigh apresenta erro nulo na avaliação da frequência naturais
( | 𝑣| = | 𝜑|𝑖 ⇒ 𝑅(| 𝜑|𝑖) = 𝜔𝑖 )

35. 35
• Teorema da Expansão
– Define que os vetores modais normalizados para as massas modais unitárias são linearmente
independentes entre si e por isso constituem uma base de dimensão n . Logo o teoreme reitera que:
– “Qualquer vetor resposta pode ser definido como uma combinação linear dos vetores modais
normalizados multiplicados pelos coeficientes 𝑐𝑖.
– Os coeficientes 𝑐𝑖 , componentes do vetor resposta na base modal, representam fisicamente o grau de
participação dos modos naturais no movimento do sistema
| 𝑥( 𝑡)| = ∑ | 𝜑|𝑖 𝑐𝑖
𝑛
𝑖=1 = [𝛷] | 𝑐 |
– O teorema da Expansão está no fundamento da análise modal, permitindo transformar as coordenadas
generalizadas nas coordenadas naturais ou modais para o sistema.
| 𝑥( 𝑡)| = ∑ | 𝜑|𝑖 𝜂𝑖(𝑡)𝑛
𝑖=1 = [𝛷] | 𝜂( 𝑡) | (expansão do vetor na base modal)
[𝛷] 𝑇[𝑚]|𝑥(𝑡)| = [𝛷] 𝑇[𝑚][𝛷] | 𝜂( 𝑡) |
[𝛷] 𝑇[𝑚]|𝑥(𝑡)| = (1) | 𝜂( 𝑡) | ⇒ | 𝜂( 𝑡) | = [𝛷] 𝑇[𝑚]|𝑥(𝑡)|
• Análise Modal ou Sobreposição modal
– Técnica de resolução do sistema da EDM para Regime Forçacdo (geralmente solicitação não
harmônica, esta apresenta uma resolução simples).
– Assenta nas propriedades de ortonormalidade dos vetores modais normalizados em relação à matriz
de massa e rigidez
– Assenta também na transformação linear ou projeção da EDM na base modal através da Matriz
Modal [𝛷] = [|𝜑|1 | 𝜑|2 … ] = [𝑇]
– As EDM na base modal estão desacopladas ou independentes, a sua resolução passa pela aplicação
das técnicas de análise usadas para 1G.L. a cada equação.
• Análise Modal para sistemas Amortecidos – Para que haja desacoplamento da matriz de amortecimento
ao projetar a EDM na base modal, é necessário que:
i) Matriz de Amortecimento Propocional: A matriz de amortecimento é dada como uma combinação
linear das matrizes de massa ou inércia e de rigidez: [𝑐] = 𝛼[𝑚] + 𝛽[𝑘]
… + [𝑐]|𝑥̇|+. . = | 𝐹| ⇒ … + [𝑐][𝜙]|𝜂̇| + ⋯ = | 𝐹| ⇒ … + [𝜙] 𝑇[𝑐][𝜙]|𝜂̇| + ⋯ = [𝜙] 𝑇| 𝐹|
… + [𝜙] 𝑇
( 𝛼[𝑚] + 𝛽[𝑘] ) [𝜙]|𝜂̇| + ⋯ = [𝜙] 𝑇| 𝐹| ⇒ … + ( 𝛼[𝐼] + 𝛽[𝛺2] ) | 𝜂̇| + ⋯ = [𝜙] 𝑇| 𝐹|
… + (2𝜉[𝛺] ) | 𝜂̇| + ⋯ = [𝜙] 𝑇| 𝐹|
ii) Obedecer à condição de Caughey:
[𝑘][𝑚]−1[𝑐] = [𝑐][𝑚]−1
[𝑘]

36. 36
• Análise Modal com Base Modal Truncada
– Vantagem: Redução significativa do esforço computacional
– Princípios: i) Modos que contribuem mais para a resposta são os modos de menor energia/menor
frequência natural
Ii) Modos com frequências próximas da banda de frequências da solicitação
Critério de Truncatura
Regime 𝜔 < 𝜔1 𝜔1 < 𝜔 < 𝜔 𝑛 𝜔 𝑛 < 𝜔
Harmônico i) ii) Todos os modos !
Periódico ? critério heurístico ? Todos os modos !
Transiente i)
– Matriz Modal Truncada: [ 𝛷] 𝑛×p = [
𝜑11 … 𝜑1𝑝
… 𝜑22 …
𝜑 𝑛1 … 𝜑 𝑝𝑛
]
– Projecção das Coordenadas Generelizadas: |𝑥(𝑡)| 𝑛×1 = [ 𝛷] 𝑛×p | 𝜂( 𝑡) | 𝑝×1
– EDM projetada na Base Modal:
[ 𝑚] 𝑛×𝑛 |𝑥̈( 𝑡)| 𝑛×1 + [ 𝑘] 𝑛×𝑛 |𝑥(𝑡)| n×1 = |𝑓(𝑡)|n×1
[ 𝛷]p×𝑛
𝑇 [ 𝑚] 𝑛×𝑛 [ 𝛷]n×𝑝|𝜂̈( 𝑡)| 𝑛×1 + [ 𝛷]p×𝑛
𝑇 [ 𝑘] 𝑛×𝑛 [ 𝛷]n×𝑝 |𝜂(𝑡)|n×1 = [ 𝛷]p×𝑛
𝑇 |𝑓(𝑡)|n×1
[ 𝐼] 𝑝×𝑝 |𝜂̈( 𝑡)| 𝑝×1 + [ 𝛺2] 𝑝×𝑝 |𝜂(𝑡)|p×1 = |𝑁(𝑡)|p×1
– Resposta nas Coordenadas Generalizadas: |𝑥(𝑡)| 𝑛×1 = [ 𝛷] 𝑛×p | 𝜂( 𝑡) | 𝑝×1

37. 37
• Paralelismo entre as abordagens de 1G.L. e 2G.L.
1G.L. 2G.L.
o Regime Livre
EDM
𝑚𝑥̈ + 𝑐𝑥̇ + 𝑘𝑥 = 0 [𝑚]|𝑥̈| + [𝑐]|𝑥̇| + [𝑘]|𝑥| = 0
solução do tipo
𝑥( 𝑡) = 𝐶𝑒 𝑠𝑡 | 𝑥( 𝑡)| = | 𝑢| cos( 𝜔𝑡 − 𝜑)
Plug-in na EDM ⇒ Problema característico
-------- (−𝜔2[𝑚] + [𝑘])|𝑢| = 0
Eq. Característica
𝑚𝑠2
+ 𝑐𝑠 + 𝑘 = 0 𝑑𝑒𝑡(−𝜔2[𝑚] + [𝑘]) = 0
Vetores Modais
| 𝑢| = |
1
1
| (−𝜔𝑖
2
[𝑚] + [𝑘])|𝑢|𝑖 = 0
𝑟1 e 𝑟2
Modos naturais
------ | 𝑥( 𝑡)|𝑖 = | 𝑢|𝑖 cos( 𝜔𝑡 − 𝜑)
Condições iniciais
𝑥0 = 𝑥(𝑡 = 0) | 𝑥0| = | 𝑥(𝑡 = 0)|
𝑥̇0 = 𝑥̇(𝑡 = 0) | 𝑥̇0| = | 𝑥̇(𝑡 = 0)|
o Regime Forçado Harmônico
solução do tipo
𝑥( 𝑡) = 𝑋̅( 𝜔) 𝑒 𝑗𝜔𝑡 | 𝑥( 𝑡)| = | 𝑋̅( 𝜔)| 𝑒 𝑗𝜔𝑡
Plug-in na EDM
(−𝜔2
𝑚 + 𝑗𝜔𝑐 + 𝑘) 𝑋̅(𝜔)𝑒 𝑗𝜔𝑡
= 𝐹𝑒 𝑗𝜔𝑡 (−𝜔2
[𝑚] + 𝑗𝜔[𝑐] + [𝑘]) | 𝑋̅ (𝜔)| 𝑒 𝑗𝜔𝑡
= | 𝐹| 𝑒 𝑗𝜔𝑡
𝑋̅( 𝜔) =
𝐹
−𝜔2 𝑚+𝑗𝜔𝑐+𝑘
[𝑍(𝜔)]|𝑋̅ (𝜔)| = | 𝐹|
Manipulação matemática:
𝑥( 𝑡) = 𝑋̅( 𝜔) 𝑒 𝑗𝜔𝑡
= 𝑋( 𝜔) cos( 𝜔𝑡 − 𝜑) | 𝑋̅ (𝜔)| = ±| 𝑋(𝜔)| cos( 𝜔𝑡)

38. 38
2.2 – Introdução
• Formalismo ou Procedimento de Lagrange – Baseado no principio Variacional de Hamilton
𝑑
𝑑𝑡
(
𝜕
𝜕𝑞̇ 𝑖
L) +
𝜕
𝜕𝑞̇ 𝑖
F −
𝜕
𝜕𝑞𝑖
L = Q i ou
𝑑
𝑑𝑡
(
𝜕
𝜕𝑞̇ 𝑖
T) +
𝜕
𝜕𝑞̇ 𝑖
F −
𝜕
𝜕𝑞𝑖
T +
𝜕
𝜕𝑞𝑖
V = Q i
em que: 𝐿 = 𝑇 – 𝑉 e Q i =
𝜕
𝜕𝑞 𝑖
(𝑊𝐹) representa as forças generalizadas nao conservativas
• Função Dissipativa de Rayleigh
𝐹 =
1
2
∑ [ 𝑐 ( 𝑣2 − 𝑣1)2 ]
𝑛
𝑗
• Medição Experimental da Rigidez:
𝑓𝑖 = 𝑘𝑖𝑗 𝑑𝑗 , 𝑑𝑖 = 𝛼𝑖𝑗 𝑓𝑗 [𝑘] = [𝑎]−1
(𝑚𝑎𝑡𝑟𝑖𝑧 𝑑𝑒 𝑓𝑙𝑒𝑥𝑖𝑏𝑖𝑙𝑖𝑑𝑎𝑑𝑒)
• Equação Diferencial do Movimento Básica
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [ 𝑐 𝑒𝑞 ] 𝑥̇ + [ 𝑘 𝑒𝑞 ] 𝑥 = 0
• Definir os Modos Naturais de Vibração (Assumindo sistema não amortecido)
| 𝑥|1 = | 𝑢|1 cos(𝜔1 𝑡 − 𝜑1)
| 𝑥|2 = | 𝑢|2 cos(𝜔2 𝑡 − 𝜑2)
• Frequencias Naturais ( Resolução Analítica )
𝑑𝑒𝑡( −𝜔2[𝑚] + [𝑘] ) = 0 ⇒
𝑠𝑜𝑙𝑣𝑒( 𝜔4[ 𝑚11 𝑚22 − 𝑚12
2 ] − 𝜔2[ 𝑚11 𝑘22 + 𝑚22 𝑘11 − 2𝑚12 𝑘12 ] + [ 𝑘11 𝑘22 − 𝑘12
2] = 0)
• Frequência Fundamental (Quociente de Rayleigh – Resuloção Aproximada)
𝑅(| 𝑣|) =
| 𝑣| 𝑇 [𝑘] | 𝑣|
| 𝑣| 𝑇 [𝑚] | 𝑣|
em que | 𝑣| = [𝐾]−1
⋅ 𝑑𝑖𝑎𝑔[𝑚]
𝑅(| 𝑣|) ≅ 𝜔1
2
⇒ 𝜔1 ≅ √𝑅(| 𝑣|)
• Vetor Modal
| 𝑢1| = |
1
𝑟1
| ; | 𝑢2| = |
1
𝑟2
| ;
𝑟1 = −
𝜔1
2 𝑚12−𝑘12
𝜔1
2 𝑚22−𝑘22
; 𝑟2 = −
𝜔2
2 𝑚12−𝑘12
𝜔2
2 𝑚22−𝑘22
𝑑
𝑑𝜃
𝑠𝑖𝑛𝜃 = cos(𝜃)
𝑑
𝑑𝜃
cos( 𝜃) = −sin(𝜃)
𝑑
𝑑𝑡
𝑠𝑖𝑛𝜃 = 𝜃̇cos(𝜃)
𝑑
𝑑𝑡
cos( 𝜃) = −𝜃̇sin(𝜃)

39. 39
• Vetor Modal Normalizado - Normalização dos vetores modais para massas modas unitárias
|𝜑 𝑖| =
1
√|𝑢𝑖| 𝑇[𝑚]|𝑢𝑖|
|𝑢1| ⇒ |𝜑 𝑖| =
1
√𝑚22 𝑟𝑖
2+2𝑚12 𝑟𝑖+𝑚11
|
1
𝑟𝑖
|
Na MAQ texas nspire: |𝜑 𝑖| =
1
√det( | 𝑢𝑖| 𝑇[𝑚]|𝑢𝑖| )
|𝑢1|
• Matriz Modal Normalizada
[𝛷] = [ | 𝜑1| | 𝜑2| ]
• Transformação para Coordendas Naturais ou Coordenadas Modais
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [ 𝑐 𝑒𝑞 ] 𝑥̇ + [ 𝑘 𝑒𝑞 ] 𝑥 = |𝐹|
[ 𝑚 𝑒𝑞 ] [𝜑] | 𝑛̈| + [ 𝑐 𝑒𝑞 ] [𝜑] | 𝑛̇| + [ 𝑘 𝑒𝑞 ] [𝜑] | 𝑛| = | 𝐹|
| 𝑛̈| + [ 𝛺 ] | 𝑛| = [𝛷] 𝑇 | 𝐹| em que [ 𝛺2 ] = [
𝜔1
2
0
0 𝜔2
2]
2.3 – Regime Livre ( Sistemas Não Amortecidos)
• Equação Diferencial do Movimento Básica
[ 𝑚 𝑒𝑞 ] 𝑥̈ + [ 𝑘 𝑒𝑞 ] 𝑥 = 0
• Resposta Livre ou Transitória– Combinação Linear dos Modos Naturais de Vibração excitados
| 𝑥( 𝑡) | = [ 𝑈 ] |
𝑐1cos(𝜔1 𝑡 − 𝜑1)
𝑐2cos(𝜔2 𝑡 − 𝜑2)
| , em que [ 𝑈 ] = ⌈
1 1
𝑟1 𝑟2
⌉
𝑐1 =
1
𝑟2−𝑟1
√( 𝑟2 𝑥1
0
− 𝑥2
0)2 +
(𝑟2 𝑥̇1
0−𝑥̇2
0)
2
𝜔1
2
𝑐1 =
1
𝑟2−𝑟1
√( 𝑟1 𝑥1
0
− 𝑥2
0)2 +
(𝑟1 𝑥̇1
0−𝑥̇2
0)
2
𝜔2
2
tan( 𝜑1) =
𝑟2 𝑥̇1
0−𝑥̇2
0
𝜔1(𝑟2 𝑥1
0−𝑥2
0)
atenção ao caso de tan(𝜑1) = 0 ( 0+
ou 0-
?? )
tan( 𝜑2) =
𝑟1 𝑥̇1
0−𝑥̇2
0
𝜔2(𝑟1 𝑥1
0−𝑥2
0)

40. 40
2.4- Regime Forçado Harmônico
2.4.1 – Introdução
• Equação Diferencial do Movimento Básica
[ 𝑚 𝑒𝑞 ] | 𝑥̈ | + [ 𝑘 𝑒𝑞 ] | 𝑥 | = | 𝐹| 𝑒 𝑗𝜔𝑡
( −𝜔2[ 𝑚 𝑒𝑞 ] + [ 𝑘 𝑒𝑞 ] ) | 𝑋( 𝜔)| = | 𝐹|
• Resposta Permanente
| 𝑥(𝑡)| = |
𝑋̅1(𝜔)
𝑋̅2(𝜔)
| cos( 𝜔𝑡)
|
𝑋̅1( 𝜔)
𝑋̅2( 𝜔)
| = [ 𝑍 ]−1 | 𝐹|
seja [ 𝑧 ] = −𝜔2[ 𝑚 ] + [𝑘] a matriz de impedâncias ou de rigidez dinâmica
O módulo de 𝑋̅𝑖( 𝜔), representa a amplitude da resposta estacionário segundo o G.L. 𝑖
O argumento de 𝑋̅𝑖( 𝜔) , representa o desfazamento entre a excitação e a resposta segundo o G.L. 𝑖
Equivalência da modelação das solicitações:
𝑓( 𝑡) = 𝐹𝑐𝑜𝑠(𝜔𝑡) | 𝑥( 𝑡)| = | 𝑋̅(𝜔)|cos(𝜔𝑡)
Ou ⇒
𝑓( 𝑡) = 𝐹𝑠𝑖𝑛(𝜔𝑡) | 𝑥( 𝑡)| = | 𝑋̅(𝜔)|sin(𝜔𝑡)

41. 41
Modelo académico: massa (secundário)-mola
Sistema Secundário
ou auxiliar
Sistema Primário
ou Principal
2.4.2 – Absorsor de Vibrações
Definição – O absorsor de vibrações (Tuned
mass dampers - TMD) consiste numa técnica de
controlo passivo de vibrações. Solução
tecnológica que pretende efectivamente
eliminar a vibração de um equipamento
através da introdução de um componente de
sacrifício (este sim que irá vibrar). O princípio
de funcionamento baseia-se na sintonização da
força de inérica do absorsor de modo ao ser
efeito dinâmico ser contrário e de igual
intensidade ao efieto dinâmico da solicitação
no primário.
Vocabolário Associado:
– Frequência de sintonização (tunning
frequency) ou condição de
Funcionamento: Frequência natural do
secundário Isolado igual à frequência de
excitação do primário
• Desvantagens do Absorsor
o A introdução do absorsor cria 2
frequencias naturais no sistema global (o primário apenas apresentava 1 frequencia natural,
considerando um sistema 1G.L).
o Absorsor para equipamentos vibratórios: A solicitação até chegar à frequência de funcionamento
passa pela 1ª frequência natural do sistema Global (pico de resposta no arranque e paragem)
o O absorsor apresenta uma gama de funcionamento eficiênte relativamente reduzida . Quando ocorre
desintonização do absorsor (variação da 𝜔 de solicitação) pode mesmo amplificar a resposta do
primário
o Apenas apresenta 1 única frequência de sintonização (frequência para a qual a resposta do primário é
teoricamente nula)
o Os tópicos anteriores restringem a sua aplicação a equipamentos com velocdiades de funcionamento
constantes ao longo do ciclo de funcionamento e entre ciclos de funcionamento (seria necessário um
ajuste do absorsor entre ciclos) e a sua aplicação torna-se complexa para sistemas com n G.L.
• Aumento da Gama de funcionamento do Absorsor
o 𝜺 ↑ ⇒ 𝑚2 ↑ , pouco conveniente
o Introdução de amortecimento (contudo a resposta nunca será nula !!!)

42. 42
Equivalência da modelação das solicitações:
𝑓( 𝑡) = 𝐹𝑐𝑜𝑠(𝜔𝑡) | 𝑥( 𝑡)| = | 𝑋̅( 𝜔) |cos(𝜔𝑡)
Ou ⇒
𝑓( 𝑡) = 𝐹𝑠𝑖𝑛(𝜔𝑡) | 𝑥( 𝑡)| = | 𝑋̅( 𝜔) |sin(𝜔𝑡)
• Parâmetros dos Sistemas Isolados
o Parâmetros adicionais de dimensionamento:
𝛼 =
𝜔 𝑛 𝑠
𝜔 𝑛 𝑝
𝛽 =
𝜔
𝜔 𝑛 𝑝
𝜀 =
𝑚2
𝑚1
𝜔 𝑛 𝑝
= √
𝑘1
𝑚1
𝜔 𝑛 𝑠
= √
𝑘2
𝑚2
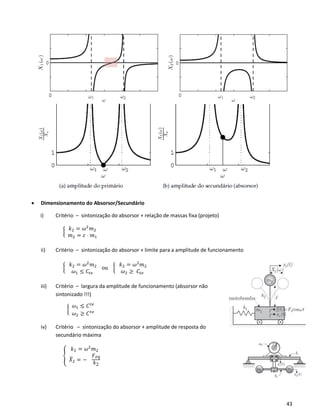
o Condição de Absorção de Vibrações:
𝜔 𝑛 𝑠 = 𝜔 = √
𝑘2
𝑚2
(1)
• Parâmetros do Sistema Global
o Resposta Forçada dos dois corpos
(Absorsor Sintonizado)
𝑋̅1 ≈ 0
𝑋̅2 = −
𝐹𝑒𝑞
𝑘1
⋅
1
𝜀𝛽2
cos(𝜔𝑡)
𝑋̅2 = −
𝐹𝑒𝑞
𝑘2
o Frequências Naturais ( Situação Genérica de 𝜔 𝑛 𝑠 ≠ 𝜔 , absorsor não sintonizado )
(1 − 𝛽2)( 𝛼2
− 𝛽2) − 𝜀𝛼4
𝛽2
= 0 Eq. Característica baseada nos parâmetros isolados
𝜔1
2
=
(𝜔 𝑛 𝑝)
2
2
[ (1 + 𝛼2
+ 𝛼2
𝜀) − √(1 + 𝛼2 + 𝛼2 𝜀)2 − 4𝛼2 ] usar expressão no critério ii)
𝜔2
2
=
(𝜔 𝑛 𝑝)
2
2
[ (1 + 𝛼2
+ 𝛼2
𝜀) + √(1 + 𝛼2 + 𝛼2 𝜀)2 − 4𝛼2 ]
( 𝑘1 + 𝑘2 − 𝜔1
2
𝑚1)( 𝑘2 − 𝜔1
2
𝑚2) = 0 (usar sistema no critério iii)
( 𝑘1 + 𝑘2 − 𝜔2
2
𝑚1)( 𝑘2 − 𝜔2
2
𝑚2) = 0
Nota de Dimensionamento:
- Dimensionamento com base em
parâmetros dos sitemas isolados
- Dualidade na nomencaltura dos
vários parâmetros (propriedades dos
sistemas isolados, propriedades dos
sitema Global)

43. 43
• Dimensionamento do Absorsor/Secundário
i) Critério – sintonização do absorsor + relação de massas fixa (projeto)
{
𝑘2 = 𝜔2
𝑚2
𝑚2 = 𝜀 ⋅ 𝑚1
ii) Critério – sintonização do absorsor + limite para a amplitude de funcionamento
{
𝑘2 = 𝜔2
𝑚2
𝜔1 ≤ 𝐶𝑡𝑒
ou {
𝑘2 = 𝜔2
𝑚2
𝜔2 ≥ 𝐶𝑡𝑒
iii) Critério – largura da amplitude de funcionamento (absorsor não
sintonizado !!!)
{
𝜔1 ≤ 𝐶 𝑡𝑒
𝜔2 ≥ 𝐶 𝑡𝑒
iv) Critério – sintonização do absorsor + amplitude de resposta do
secundário máxima
{
𝑘2 = 𝜔2
𝑚2
𝑋̅2 = −
𝐹 𝑒𝑞
𝑘2

44. 44
2.5 – Regime Forçado Transiente
• Procedimento da Análise Modal:
1º) Calcular o vetor solicitação nas Coordenadas Naturais
2º) Calcular a resposta nas coordenadas modais ou naturais (Pelas técnicas aplicadas a sistemas com 1 G.L.,
isto porque trata-se de um sistema de ED desacoplado)
3º) Determinar a resposta nas coordenadas generalizadas pelo conceito de matriz de transformação
• EDM nas Coordenadas Naturais
[𝐼]| 𝑛̈( 𝑡) | + [𝛺2] | 𝑛( 𝑡) | = [𝛷] 𝑇 | 𝑓(𝑡)| = | 𝑁| em que [𝛺2] = [
𝜔1
2
0
0 𝜔2
2] e [𝐼] = [
1 0
0 1
]
{
𝑛1̈ ( 𝑡) + 𝜔1
2
𝑛1( 𝑡) = 𝜑11 𝑓1( 𝑡) + 𝜑21 𝑓2( 𝑡) = 𝑁1
𝑛2̈ ( 𝑡) + 𝜔2
2
𝑛2( 𝑡) = 𝜑12 𝑓1( 𝑡) + 𝜑22 𝑓2( 𝑡) = 𝑁2
• Vetor Solicitação nas Cordenadas Naturais
|
𝑁1(𝑡)
𝑁2(𝑡)
| = [
𝜑11 𝜑12
𝜑21 𝜑22
]
𝑇
|
𝑓1(𝑡)
𝑓2(𝑡)
|
• Resposta nas Coordenadas Generalizadas :
|
𝑥1(𝑡)
𝑥2(𝑡)
| = [
𝜑11 𝜑12
𝜑21 𝜑22
] |
𝑛1(𝑡)
𝑛2(𝑡)
|
• Resposta Natural ao Transiente Degrau / Degrau unitário ( 𝝃 = 𝟎 ) :
𝜂𝑖( 𝑡) =
𝑁 𝑖
𝜔𝑖
2 [ 1 − cos( 𝜔𝑖 𝑡) ]
• Resposta Natural ao Transiente Rectangular ( 𝝃 = 𝟎 ) :
𝜂𝑖( 𝑡) =
• Resposta Natural a meia onda sin ( 𝝃 = 𝟎 ) :
𝜂𝑖( 𝑡) =
𝑁 𝑖
𝜔1
2
[ 1 − cos( 𝜔𝑖 𝑡) ] para 𝑡 ≤ 𝑡 𝑐
𝑁 𝑖
𝜔 𝑖
2
[ cos[ 𝜔𝑖( 𝑡 − 𝑡 𝑐) ] − cos( 𝜔𝑖 𝑡) ] para 𝑡 > 𝑡 𝑐
𝑁 𝑖
𝜔1
2
𝜔𝑖⋅𝑡 𝑐
[ (𝜔𝑖⋅𝑡 𝑐)2−𝜋2]
⋅ [ 𝜔𝑖 𝑡 𝑐 sin(
𝜋
𝑡 𝑐
⋅ 𝑡) − 𝜋sin( 𝜔𝑖 𝑡) ] para 𝑡 ≤ 𝑡 𝑐
𝑁 𝑖
𝜔𝑖
2
𝜔 𝑖 𝜋 tc
[ 𝜋2− (𝜔𝑖⋅𝑡 𝑐)2]
[ sin[ 𝜔𝑖( 𝑡 − 𝑡 𝑐)] + sin( 𝜔𝑖 𝑡) ] para 𝑡 > 𝑡 𝑐

45. 45
3- Sistemas Contínuos (Equação Diferencial Linear Parcial Homogênea)
3.1- Glossário
• Hipotese de resolução da EDM – O primeiro passo para a resolução de uma ED homogenia (EDM em
regime livre) é encontrar um conjunto de soluções particulares de modo a obter a solução geral por
combinação linear das soluções particulares.. A hipótese de resolução será a seguinte:
“Movimento Harmonico síncrono sem desfazamento entre as massas infinitesimais do sistema, às
frequências naturais 𝜔𝑖 , em regime livre. Isto é, a sua configuração espacial do sistema não varia com o
tempo. Por outras palavras, todas as secções do sistema atingem as suas posições extremas e de equilibrio
estático ao mesmo tempo, ou seja, executam o mesmo tipo de movimento.”
• Equação Diferencial de Movimento (EDM) – Equação diferencial, linear, de derivadas parciais, não
homogênia
𝜕
𝜕𝑥
(𝑘( 𝑥)
𝜕
𝜕𝑥
𝑢(𝑥, 𝑡)) + 𝑓(𝑥, 𝑡) = 𝑚( 𝑥)
𝜕2
𝜕𝑡2
𝑢( 𝑥, 𝑡)
𝜕2
𝜕𝑥2
(𝑘( 𝑥)
𝜕2
𝜕𝑥2
𝑣(𝑥, 𝑡)) + 𝑚( 𝑥)
𝜕2
𝜕𝑡2
𝑣( 𝑥, 𝑡) = 𝑓(𝑥, 𝑡)
• Problema Característico – Problema de valores característicos e funções características. Equação
resultante da aplicação do metodo de separação de variáveis cujas soluções V(x) respeitam a EDM, têm em
conta a geometria e condições de fronteira, e asseguram soluções nao triviais para a EDM
𝜕
𝜕𝑥
(𝑘( 𝑥)
𝜕
𝜕𝑥
𝑈( 𝑥) ) + 𝜔2
𝑚(𝑥) 𝑈( 𝑥) = 0
𝜕2
𝜕𝑥2
(𝑘( 𝑥)
𝜕
𝜕𝑥
𝑉( 𝑥) ) = 𝜔2
𝑚(𝑥) 𝑉( 𝑥)
• Equação Característica – Equação que assegura que existe soluções não nulas para as funções
características. Resulta da aplicação das condições fronteira às formas naturais
Equação da forma: 𝑓( 𝜔, 𝑐, 𝑙) = 0
• Modos Naturais 𝒗(𝒙, 𝒕)
– Infinidade de soluções particulares da EDM homogênia para as quais o movimento harmônico
síncrono às frequências naturais 𝜔𝑖 , em regime livre, é possível
– Definidas por um par característico ( 𝜔𝑖 , 𝑉𝑖( 𝑥) ) obtido a partir das soluções do Problema
Característico
– Propriedade intrínseca do sistema, função apenas das propriedades mecânicas do sistema
Definidos por: 𝑣 𝑛( 𝑥, 𝑡) = 𝑉𝑛( 𝑥) ⋅ 𝑔 𝑛( 𝑡) = 𝑉𝑛( 𝑥) ⋅ [ 𝐶 𝑛 cos( 𝜔 𝑛 𝑡) +Dnsin( 𝜔 𝑛 𝑡) ]

46. 46
• Funções Caracteristicas 𝑽 𝒏(𝒙) ( = Vetores Modais)
– Soluções não triviais do problema característico, para cada frequência natural 𝜔𝑖 e verificam a EDM e
asseguram as condições de Fronteira e geometria do sistema.
– Formas naturias de Vibração. representam a configuração espacial do sistema no movimento
harmônico síncrono em regime livre ou natural correspondente a uma determinada frequência
natural .
– As funções características sao da forma: 𝑉𝑛(𝑥) = 𝐴 cos (
𝜔 𝑛
𝑐
𝑥) + 𝐵 sin (
𝜔 𝑛
𝑐
𝑥)
em que 𝑐2
=
𝑘(𝑥)
𝑚(𝑥)
• Frequências Naturais
– Soluções / Raízes não triviais da Equação característica
– Frequências para as quais o movimento harmônico síncrono sem desfasamento, em regime livre é
possível.
– Valores Característicos , valroes particulares de ω2
para os quais as funções características
apresentam valores não nulos.
• Condições de Fronteira – Definiem os valores característicos 𝜔2
, e as constantes das formas naturais
com excepção de uma constante. As formas naturais associadas a uma frequência natural estão definidas a
menos de uma constante (que não foi definida pelas condições fronteira)
A aplicação das condições Fronteira cria um Novo Problema Característico, cujos valores prórpios são as
frequências naturais e os vetores próprios as constantes das formas características
O problema característico resultante da aplicação das C.F. será da forma:
[ ] |
𝐴
𝐵
| = |
0
0
|

47. 47
• Normalização das funções características para as massas modais unitárias – As formas naturais 𝑈 𝑛( 𝑥)
associadas a uma frequência natural 𝜔 𝑛 estão definidas a menos de uma constante. Para determinar essa
constante é necessário normalizar a função característica através da expressão seguinte:
∫ 𝑚(𝑥) [ 𝜙 𝑛( 𝑥) ]2
𝑑𝑥 = 1
𝑙
0
• Propriedades de Ortogonalidade das funções características:
Sistema Ortogonalidade em relação à 𝒎(𝒙) Ortogonalidade em relação à 𝒌(𝒙)
Barras, Veios ∫ 𝑢 𝑟( 𝑥, 𝑡) 𝑚( 𝑥) 𝑢 𝑠( 𝑥, 𝑡) 𝑑𝑥 = 0
𝑙
0
∫
𝜕
𝜕𝑥
𝑢 𝑟( 𝑥, 𝑡) 𝑘( 𝑥)
𝜕
𝜕𝑥
𝑢 𝑠( 𝑥, 𝑡) 𝑑𝑥 = 0
𝑙
0
Vigas ∫ 𝑣𝑟( 𝑥, 𝑡) 𝑚( 𝑥) 𝑣𝑠( 𝑥, 𝑡) 𝑑𝑥 = 0
𝑙
0
∫
𝜕
𝜕𝑥2
𝑣𝑟( 𝑥, 𝑡) 𝑘( 𝑥)
𝜕
𝜕𝑥2
𝑣𝑠( 𝑥, 𝑡) 𝑑𝑥 = 0
𝑙
0
• Propriedades de Ortonormalidade das funções características normalizadas para as massas modais
unitárias:
Sistema Ortonormalidade em relação à 𝒎(𝒙) Ortonormalidade em relação à 𝒌(𝒙)
Barras
Veios
∫ 𝜑𝑟( 𝑥, 𝑡) 𝑚( 𝑥) 𝜑𝑠( 𝑥, 𝑡) 𝑑𝑥 = 𝛿 𝑟𝑠
𝑙
0
𝛿 𝑟𝑠 = {
1 , 𝑟 = 𝑠
0 , 𝑟 ≠ 𝑠
∫
𝜕
𝜕𝑥
𝜑𝑟( 𝑥, 𝑡) 𝑘( 𝑥)
𝜕
𝜕𝑥
𝜑𝑠( 𝑥, 𝑡) 𝑑𝑥 = 𝜔𝑟
2
𝛿 𝑟𝑠
𝑙
0
𝛿 𝑟𝑠 = {
1 , 𝑟 = 𝑠
0 , 𝑟 ≠ 𝑠
Vigas
∫ 𝜑 𝑟
( 𝑥, 𝑡) 𝑚( 𝑥) 𝜑 𝑠
( 𝑥, 𝑡) 𝑑𝑥 = 𝛿 𝑟𝑠
𝑙
0
𝛿 𝑟𝑠 = {
1 , 𝑟 = 𝑠
0 , 𝑟 ≠ 𝑠
∫
𝜕
𝜕𝑥2
𝜑𝑟( 𝑥, 𝑡) 𝑘( 𝑥)
𝜕
𝜕𝑥2
𝜑𝑠( 𝑥, 𝑡) 𝑑𝑥 = 𝜔𝑟
2
𝛿 𝑟𝑠
𝑙
0
𝛿 𝑟𝑠 = {
1 , 𝑟 = 𝑠
0 , 𝑟 ≠ 𝑠
𝛿 𝑟𝑠 – Símbolo de Kronecker

48. 48
• Expansão de uma Função em Serie de Fourier – Qualquer função periódica pode ser definida como uma
serie de harmîonicos multiplicada pelos coeficientes de Fourier (soma infinita de funções harmônicas
𝑓( 𝑡) =
𝐹0
2
+ ∑ 𝐴 𝑝 cos( 𝑝𝜔𝑡)
∞
𝑝=1
+ ∑ 𝐵𝑝 𝑓 sin( 𝑝𝜔𝑡)
∞
𝑝=1
Resposta Livre ou Natural – Corresponde à combinação linear dos diferentes modos naturais de vibração,
juntamente com a aplicação das Condições Iniciais.
𝑣( 𝑥, 𝑡) = ∑ 𝑣 𝑛(𝑥, 𝑡)
∞
𝑛=1
= ∑ 𝑉𝑛( 𝑥) 𝑔 𝑛(𝑡)
∞
𝑛=1
= ∑ 𝑉𝑛( 𝑥)
∞
𝑛=1
[ 𝐶 𝑛 cos( 𝜔 𝑛 𝑡) + 𝐷 𝑛 sin( 𝜔 𝑛 𝑡) ]
Aplicação das Condições Iniciais:
𝑣0 = 𝑣( 𝑥, 0) = ∑ 𝑉𝑛( 𝑥)
∞
𝑛=1
[ 𝐶 𝑛 ]
𝑣̇0 = 𝑣( 𝑥, 0) = ∑ 𝑉𝑛( 𝑥)
∞
𝑛=1
[ 𝜔 𝑛 𝐷 𝑛]
Consoante a função característica, as constantes 𝐶 𝑛 e 𝐷 𝑛 podem ser assemelhadas a um dos coeficientes
de Fourier ( 𝐴 𝑝 𝑜𝑢 𝐵𝑝 ) :
Expressão de 𝒗 𝟎(𝒙) 𝑪 𝒏 𝑫 𝒏
Ancos ( 𝜔 𝑛 𝑥)
2
𝐴 𝑛 ⋅ 𝑙
∫ 𝑣0( 𝑥) cos( 𝜔 𝑛 𝑥) 𝑑𝑥
𝑙
0
2
𝜔 𝑛 ⋅ 𝐴 𝑛 ⋅ 𝑙
∫ 𝑣̇0( 𝑥) cos( 𝜔 𝑛 𝑥) 𝑑𝑥
𝑙
0
Ansin( 𝜔 𝑛 𝑥)
2
𝐴 𝑛 ⋅ 𝑙
∫ 𝑣0( 𝑥) sin( 𝜔 𝑛 𝑥) 𝑑𝑥
𝑙
0
2
𝜔 𝑛 ⋅ 𝐴 𝑛 ⋅ 𝑙
∫ 𝑣̇0( 𝑥) sin( 𝜔 𝑛 𝑥) 𝑑𝑥
𝑙
0

49. 49
• Resposta Forçada – A resposta ou solução da EDM corresponde à combinação linear das diferentes formas
naturais de vibração normalizadas para as massas modais (multiplicadas pelas coordenadas modais ou
naturais).
o Expansão dos modos naturais de vibração na base modal
𝑣( 𝑥, 𝑡) = ∑ 𝜑𝑟( 𝑥) 𝜂 𝑟(𝑡)
∞
𝑛=1
o Separação da solicitação na sua componente espacial e temporal
𝑓( 𝑥, 𝑡) = 𝑝( 𝑥) 𝑔(𝑡)
o EDM
𝜕
𝜕𝑥2
(𝐸𝐼( 𝑥)
𝜕
𝜕𝑥2
𝑣(𝑥, 𝑡)) + 𝑚( 𝑥)
𝜕2
𝜕𝑡2
𝑣( 𝑥, 𝑡) = 𝑓(𝑥, 𝑡)
o EDM projectada na Base Modal
𝜕
𝜕𝑥2
(𝐸𝐼(𝑥)
𝜕
𝜕𝑥2
∑ 𝜑𝑟( 𝑥) 𝜂 𝑟(𝑡)
∞
𝑛=1
) + 𝑚( 𝑥)
𝜕2
𝜕𝑡2
∑ 𝜑𝑟( 𝑥) 𝜂 𝑟(𝑡)
∞
𝑛=1
= 𝑝( 𝑥) 𝑔(𝑡)
𝜕
𝜕𝑥2
(𝐸𝐼(𝑥) ∑ 𝜂 𝑟( 𝑡)
𝜕
𝜕𝑥2
𝜑𝑟( 𝑥)
∞
𝑛=1
) + 𝑚( 𝑥) ∑ 𝜑𝑟( 𝑥) 𝜂̈ 𝑟(𝑡)
∞
𝑛=1
= 𝑝( 𝑥) 𝑔(𝑡)
Multiplicando pela função caracterrística normalizada 𝜑𝑠 ,
Integrando 2x vezes entre 0 e 𝑙
Aplicando as condições Fronteira e por fim...
Aplicando as propriedades de ortonormalidade em relação à massa e rigidez das funções
características normalizadas
o A EDM projectada na Base Modal consiste num conjunto de Equações Diferenciais Ordinárias e
Independentes, e são dadas por:
𝜂̈ 𝑟( 𝑡) + 𝜔𝑟
2
𝜂 𝑟( 𝑡) = 𝑁𝑟( 𝑡) = (∫ 𝜑𝑟 𝑝( 𝑥) 𝑑𝑥
𝑙
0
) 𝑔(𝑡)
o Resposta Generalizada
𝑣( 𝑥, 𝑡) = ∑ 𝜑𝑟 𝜂 𝑟(𝑡)
∞
𝑟=1

50. 50
• Truncatura da Série de Resposta generalizada
A resposta generalizada em deslocamento pode ser obtida por: 𝑣( 𝑥, 𝑡) = ∑ 𝜑𝑟 𝜂 𝑟(𝑡)∞
𝑟=1 . A contribuição
das formas naturais depende do tipo de resposta a determinar
- Resposta em deslocamento: Varia na razão inversa a 𝑠4
- Resposta em momento fletor: Varia na razão inversa de 𝑠2
- Resposte Esforço Transverso: Varia na razão inversa de 𝑠
O critério de truncatura é assim função do objetivo do estudo, contudo notar que as formas de menor
energia são as que contirbuem mais para a resposta genérica do sistema.
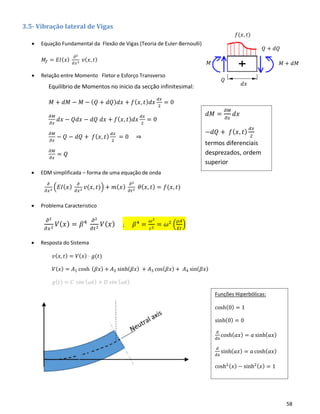
• Princípio de Hamilton – Formulação Variacional que permite o estabelecimento das EDM. O princípio
afirma que: “Num sistema mecânico, a variação da Energia Cinética mais a variação da Energia Potencial
mais a variação do Trabalho das Forças não conservaticas num intervalo qualquer entre 𝑡1 e 𝑡2 é
necesariamente nula.”
∫ 𝛿( 𝑇 − 𝑉) 𝑑𝑡
𝑡2
𝑡1
+ ∫ 𝛿𝑊𝑓𝑛𝑐
𝑡2
𝑡2
𝑑𝑡 = 0
Instantaneamente Variação
Energia Cinética 𝑇 = ∫ 𝑚(𝑥) [
𝜕
𝜕𝑡
𝑢( 𝑥, 𝑡) ]
2
𝑑𝑥
𝑙
0
𝛿𝑇 = ∫ 𝑚(𝑥) 𝛿 [
𝜕
𝜕𝑡
𝑢( 𝑥, 𝑡) ]
2
𝑑𝑥
𝑙
0
Energia Potencial
𝑉 = ∫ 𝑘( 𝑥) [
𝜕
𝜕𝑥
𝑢( 𝑥, 𝑡) ]
2
𝑙
0
𝑑𝑥
𝑉 = ∫ 𝑘( 𝑥) [
𝜕2
𝜕𝑥2
𝑣( 𝑥, 𝑡) ]
2𝑙
0
𝑑𝑥
𝛿𝑉 = ∫ 𝑘( 𝑥) 𝛿 [
𝜕
𝜕𝑥
𝑢( 𝑥, 𝑡) ]
2
𝑙
0
𝑑𝑥
𝛿𝑉 = ∫ 𝑘( 𝑥) 𝛿 [
𝜕2
𝜕𝑥2
𝑣( 𝑥, 𝑡) ]
2𝑙
0
𝑑𝑥
Trabalho FNC 𝑊𝑓𝑛𝑐 = ∫ 𝑓( 𝑥, 𝑡) 𝑢(𝑥, 𝑡) 𝑑𝑥
𝑙
0
𝛿𝑊𝑓𝑛𝑐 = ∫ 𝑓( 𝑥, 𝑡) 𝛿𝑢(𝑥, 𝑡)𝑑𝑥
𝑙
0

51. 51
• Paralelismo entre as abordagens de 1G.L. e 2G.L.
n G.L. Sistemas Continuos
o Regime Livre
EDM
[𝑚]|𝑥̈| + [𝑐]|𝑥̇| + [𝑘]|𝑥| = 0
𝜕
𝜕𝑥
(𝑘(𝑥)
𝜕
𝜕𝑥
𝑣(𝑥, 𝑡)) = 𝑚( 𝑥)
𝜕2
𝜕𝑡2 𝑣( 𝑥, 𝑡)
Hipotese de Resolução ⇒ solução do tipo
| 𝑥( 𝑡)| = | 𝑢| cos( 𝜔𝑡 − 𝜑) 𝑣( 𝑥, 𝑡) = 𝑉( 𝑥) 𝑔(𝑡)
Plug-in na EDM ⇒ Problema característico
(−𝜔2[𝑚] + [𝑘])|𝑢| = 0
𝜕
𝜕𝑥
(𝑘(𝑥)
𝜕
𝜕𝑥
𝑉( 𝑥) ) + 𝜔2
𝑚(𝑥) 𝑉( 𝑥) = 0
Obrigatoriedade matemática ---- Aplicação das “Condições Fronteira”
𝑑𝑒𝑡(−𝜔2[𝑚] + [𝑘]) = 0 𝑣( 𝑜, 𝑡) = ⋯
𝑣( 𝑙, 𝑡) = ⋯
A e B
Eq. Característica
𝑠𝑜𝑙𝑣𝑒 [𝑑𝑒𝑡(−𝜔2[𝑚] + [𝑘]) = 0] 𝑓(𝜔, 𝑐, 𝑙) = 0
Vetores Modais ---- Funções Características
(−𝜔𝑖
2
[𝑚] + [𝑘])|𝑢|𝑖 = 0 𝑉( 𝑥) = 𝐴𝑐𝑜𝑠 (
𝜔
𝑐
𝑥) + 𝐵𝑠𝑖𝑛 (
𝜔
𝑐
𝑥)
𝑟1 e 𝑟2
Modos naturais
| 𝑥( 𝑡)|𝑖 = | 𝑢|𝑖 cos( 𝜔𝑖 𝑡 − 𝜑) 𝑣 𝑛( 𝑥, 𝑡) = 𝑉𝑛( 𝑥) [ 𝐶 𝑛 𝑐𝑜𝑠( 𝜔𝑡𝑥) + 𝐷 𝑛 𝑠𝑖𝑛( 𝜔𝑡) ]
Resposta Livre
| 𝑥( 𝑡)| = [𝛷] |
𝑐1 cos( 𝜔1 𝑡 − 𝜑1)
𝑐2 cos( 𝜔2 𝑡 − 𝜑2)
| 𝑣( 𝑥, 𝑡) = ∑ 𝑉𝑛( 𝑥) [ 𝐶 𝑛 𝑐𝑜𝑠( 𝜔𝑡𝑥) + 𝐷 𝑛 𝑠𝑖𝑛( 𝜔𝑡) ]∞
𝑛
Verificação das Condições iniciais
| 𝑥0| = | 𝑥(𝑡 = 0)|
| 𝑥̇0| = | 𝑥̇( 𝑡 = 0)|

52. 52
3.2- Vibração Lateral de Cordas
• EDM simplificada – forma de uma equação de onda
𝜕
𝜕𝑥
(
𝜕
𝜕𝑥
𝑇( 𝑥) 𝑣(𝑥, 𝑡)) = 𝑚(𝑥)
𝜕2
𝜕𝑡2 𝑣( 𝑥, 𝑡)
𝜕2
𝜕𝑥2 𝑉( 𝑥) =
1
𝐶2
𝜕2
𝜕𝑡2 𝑉( 𝑥) , 𝐶2
=
𝑇
𝜇
• Problema Característico
𝜕
𝜕𝑥
(𝑇( 𝑥)
𝜕
𝜕𝑥
𝑉(𝑥)) + 𝜔2
𝑚( 𝑥) 𝑉(𝑥) = 0
• Resposta do Sistema
𝑣( 𝑥, 𝑡) = 𝑉( 𝑥) ⋅ 𝑔(𝑡)
𝑉( 𝑥) = 𝐴 cos (
𝜔
𝑐
𝑥) + 𝐵 𝑠𝑖𝑛 (
𝜔
𝑐
𝑥)
𝑔( 𝑡) = 𝐶 cos ( 𝜔𝑡) + 𝐷 𝑠𝑖𝑛 ( 𝜔𝑡)
• Confições Fronteira Possíveis
Exemplos de String vibration Behaviour:
- Vibração induzido por escoamento (flow induced
vibration) devido às forças de arrasto e elevação (Drag
and Lift Forces ) provocada pelos vortices de distruição
da camada limite,
- Em: cabos de aço e veios cilíndricos longos em
Plataformas petrolíferas, boias sinalizadoras, tubos
subaquáticos, tirantes ,etc
- Elementos Mecânicos sem capacidade de absorção
de momentos
C.F. Geométricas
𝑣(0, 𝑡) = 0 apoio duplo/encastramento
C.F. Naturais
𝑇
𝜕
𝜕𝑥
𝑣( 𝑙, 𝑡) = 0
𝑇
𝜕
𝜕𝑥
𝑣( 𝑙, 𝑡) = ± 𝑘𝑣( 𝑙, 𝑡) ± 𝑐
𝜕
𝜕𝑡
𝑣( 𝑙, 𝑡) ± 𝑚
𝜕2
𝜕𝑡2 𝑣(𝑙, 𝑡)
𝑥
𝑣(𝑥, 𝑡)

53. 53
• Condições de Fronteira: fixa - fixa
o Equação de Frequências
sin (
𝜔
𝑐
𝑙) = 0
o Frequências Naturais
𝜔 𝑛 =
𝜋𝑛𝑐
𝑙
, 𝑛 = 1,2,3 …
o Equação dos Modos Naturais de Vibração
𝑉𝑛( 𝑥) = 𝐵 sin(
𝜋𝑛
𝑙
𝑥 )
• Condição de Fronteira: fixa – pin/slot (“Livre”)
o Equação de Frequências
cos (
𝜔
𝑐
𝑙) = 0
o Frequênicas Naturais
𝜔 𝑛 =
𝜋𝑛𝑐
𝑙
−
𝜋𝑐
2𝑙
o Equação dos Modos Naturais de Vibração
𝑉𝑛( 𝑥) = 𝐵 sin(
𝜋𝑛
𝑙
𝑥 −
𝜋
2𝑙
𝑥)
• Condição de Fronteira: pin/slot (“Livre”) – fixa
o Equação de Frequências
cos (
𝜔
𝑐
𝑙) = 0
o Frequências Naturais
𝜔 𝑛 =
𝜋𝑛𝑐
𝑙
−
𝜋𝑐
𝑙
o Equação dos Modos Naturais de Vibração
𝑉𝑛( 𝑥) = 𝐴 cos (
𝜋𝑛
𝑙
𝑥 −
𝜋
2𝑙
𝑥)

54. 54
• Condição de Fronteira: pin/slot (“Livre”) – pin/slot (“Livre”)
o Equação de Frequências
sin (
𝜔
𝑐
𝑙) = 0
o Frequências Naturais
𝜔 𝑛 =
𝜋𝑛𝑐
𝑙
o Equação das Formas Naturais de Vibração
𝑉𝑛( 𝑥) = 𝐴 cos (
𝜋𝑛
𝑙
𝑥)
• Vibração Livre de Cordas
o Standing wave pattern/vibration –
excitação da corda segundo uma dada
frequência natural (há infinitas!). Neste
caso a reflexão das ondas é tal ordem
perfeita que não ha o efeito de wave
traveling ao longo da corda
o Travelling wave pattern/vibration – resposta da corda resulta da excitação de várias frequencias
naturais. Neste caso há interferência das reflexões das ondas quando atingem os extremos.
Consegue-se observar a propagação da crista da onda.

55. 55
3.3- Vibração Longitudinal de Barras
• Equação da Elasticidade de Barras
𝑃( 𝑥, 𝑡) = 𝐴𝐸( 𝑥)
𝜕
𝜕𝑥
𝑢(𝑥, 𝑡)
• EDM simplificada – forma de uma equação de onda
𝜕
𝜕𝑥
(𝐸𝐴( 𝑥)
𝜕
𝜕𝑥
𝑢( 𝑥, 𝑡)) + 𝑓( 𝑥, 𝑡) = 𝑚(𝑥)
𝜕2
𝜕𝑡2 𝑈( 𝑥)
𝜕2
𝜕𝑥2 𝑢( 𝑥, 𝑡) =
1
𝐶2
𝜕2
𝜕𝑡2 𝑢( 𝑥, 𝑡) , 𝐶2
=
𝐸
𝜌
• Problema Característico
𝜕
𝜕𝑥
(𝐸𝐴( 𝑥)
𝜕
𝜕𝑥
𝑈(𝑥)) + 𝜔2
𝑚( 𝑥) 𝑈(𝑥) = 0
• Resposta do Sistema
𝑢( 𝑥, 𝑡) = 𝑈( 𝑥) ⋅ 𝑔(𝑡)
𝑈( 𝑥) = 𝐴 cos (
𝜔
𝑐
𝑥) + 𝐵 𝑠𝑖𝑛 (
𝜔
𝑐
𝑥)
𝑔( 𝑡) = 𝐶 cos ( 𝜔𝑡) + 𝐷 𝑠𝑖𝑛 ( 𝜔𝑡)
• Condições Fronteira Possíveis:
Exemplos de Vibração Longitudinal:
- Vibração nas ferramentas de percursão de
martelos pneumáticos
- Vibração em serrotes industriais (introduzida
pelos dentes)
- Toda a acústica e seus problemas (som é uma
onda mecânica de propagação longitudinal.
Notar apenas que nenhuma onda
eletromagnética propaga-se longitudinalmente,
apenas transversalmente)
C.F. Geométricas
𝑢(0, 𝑡) = 0
C.F. Naturais
𝑃( 𝑙, 𝑡) = 0 ⇒ 𝐸𝐴
𝜕
𝜕𝑥
𝑢( 𝑙, 𝑡) = 0
𝑃( 𝑙, 𝑡) = ±𝑘𝑢( 𝑙, 𝑡) ± 𝑐
𝜕
𝜕𝑡
𝑢( 𝑙, 𝑡) ± 𝑚
𝜕2
𝜕𝑡2 𝑢( 𝑙, 𝑡) ⇒ 𝐸𝐴
𝜕
𝜕𝑥
𝑢( 𝑙, 𝑡) = ±⋯
𝑥
𝑢(𝑥, 𝑡)

56. 56

57. 57
3.4- Vibração Torsional de Veios
• Equação Fundamental da Torção de Veios (Relação da Elasticidade)
𝑀 𝑇 = 𝐺 𝐼 𝑝( 𝑥)
𝜕
𝜕𝑥
𝜃(𝑥, 𝑡)
• Equação Diferencial do Movimento
𝜕
𝜕𝑥
(𝐺𝐼 𝑝( 𝑥)
𝜕
𝜕𝑥
𝜃(𝑥, 𝑡)) + 𝑓(𝑥, 𝑡) = 𝑚( 𝑥)
𝜕2
𝜕𝑡2 𝜃(𝑥, 𝑡)
• Problema Característico
𝜕
𝜕𝑥
(𝐺𝐼 𝑝( 𝑥)
𝜕
𝜕𝑥
𝛩(𝑥)) + 𝜔2
𝐽( 𝑥) 𝛩(𝑥) = 0
• Resposta do Sistema
𝑢( 𝑥, 𝑡) = 𝛩( 𝑥) ⋅ 𝑔(𝑡)
𝑈( 𝑥) = 𝐴 cos (
𝜔
𝑐
𝑥) + 𝐵 𝑠𝑖𝑛 (
𝜔
𝑐
𝑥)
𝑔( 𝑡) = 𝐶 cos ( 𝜔𝑡) + 𝐷 𝑠𝑖𝑛 ( 𝜔𝑡)
• Condições Fronteira Possíveis:
Nomenclatura
Geometria de Massas:
𝐽𝑣𝑒𝑖𝑜 = 𝐽( 𝑥) 𝑙
𝐽( 𝑥) = 𝜌 𝐼 𝑝
𝐽𝑣𝑒𝑖𝑜 = 𝜌 𝐼 𝑝 𝑙
C.F. Geométricas
𝜃(0, 𝑡) = 0
C.F. Naturais
𝑀𝑡( 𝑙, 𝑡) = 0 ⇒ 𝐺𝐼 𝑝
𝜕
𝜕𝑥
𝜃( 𝑙, 𝑡) = 0
𝑀𝑡( 𝑙, 𝑡) = ±𝑘𝜃( 𝑙, 𝑡) ± 𝑐
𝜕
𝜕𝑡
𝜃( 𝑙, 𝑡) ± 𝐽𝑣𝑜𝑙𝑎𝑛𝑡𝑒
𝜕2
𝜕𝑡2 𝑐 ⇒ 𝐺𝐼 𝑝
𝜕
𝜕𝑥
𝜃( 𝑙, 𝑡) = ± …
𝜃(𝑥, 𝑡)
𝑀𝑡(𝑥, 𝑡)

58. 58
𝑀 + 𝑑𝑀
𝑄 + 𝑑𝑄
𝑄
𝑀
𝑑𝑥
𝑓(𝑥, 𝑡)
3.5- Vibração lateral de Vigas
• Equação Fundamental da Flexão de Vigas (Teoria de Euler-Bernoulli)
𝑀𝑓 = 𝐸𝐼( 𝑥)
𝜕2
𝜕𝑥2 𝑣( 𝑥, 𝑡)
• Relação entre Momento Fletor e Esforço Transverso
• EDM simplificada – forma de uma equação de onda
𝜕
𝜕𝑥2 (𝐸𝐼( 𝑥)
𝜕
𝜕𝑥2 𝑣(𝑥, 𝑡)) + 𝑚( 𝑥)
𝜕2
𝜕𝑡2 𝜃( 𝑥, 𝑡) = 𝑓(𝑥, 𝑡)
• Problema Caracteristico
𝜕2
𝜕𝑥2
𝑉( 𝑥) = 𝛽4 𝜕2
𝜕𝑡2
𝑉( 𝑥) ; 𝛽4
=
𝜔2
𝑐2
= 𝜔2
(
𝜌𝐴
𝐸𝐼
)
• Resposta do Sistema
𝑣( 𝑥, 𝑡) = 𝑉( 𝑥) ⋅ 𝑔(𝑡)
𝑉( 𝑥) = 𝐴1 cosh ( 𝛽𝑥) + 𝐴2 sinh( 𝛽𝑥) + 𝐴3 cos( 𝛽𝑥) + 𝐴4 sin( 𝛽𝑥)
𝑔( 𝑡) = 𝐶 cos ( 𝜔𝑡) + 𝐷 𝑠𝑖𝑛 ( 𝜔𝑡)
Equilibrio de Momentos no inicio da secção infinitesimal:
𝑀 + 𝑑𝑀 − 𝑀 − ( 𝑄 + 𝑑𝑄) 𝑑𝑥 + 𝑓( 𝑥, 𝑡) 𝑑𝑥
𝑑𝑥
2
= 0
𝜕𝑀
𝜕𝑥
𝑑𝑥 − 𝑄𝑑𝑥 − 𝑑𝑄 𝑑𝑥 + 𝑓( 𝑥, 𝑡) 𝑑𝑥
𝑑𝑥
2
= 0
𝜕𝑀
𝜕𝑥
− 𝑄 − 𝑑𝑄 + 𝑓( 𝑥, 𝑡)
𝑑𝑥
2
= 0 ⇒
𝜕𝑀
𝜕𝑥
= 𝑄
𝑑𝑀 =
𝜕𝑀
𝜕𝑥
𝑑𝑥
−𝑑𝑄 + 𝑓( 𝑥, 𝑡)
𝑑𝑥
2
termos diferenciais
desprezados, ordem
superior
Funções Hiperbólicas:
cosh(0) = 1
sinh(0) = 0
d
dx
cosh( 𝑎𝑥) = 𝑎 sinh( 𝑎𝑥)
d
dx
sinh( 𝑎𝑥) = 𝑎 cosh( 𝑎𝑥)
cosh2( 𝑥) − sinh2( 𝑥) = 1

59. 59
• Condições Fronteira Possíveis:
C.F. Geométricas
𝑣(0, 𝑡) = 0
𝜕
𝜕𝑥
𝑣(0, 𝑡) = 0
C.F. Naturais
𝑀𝑓( 𝑙, 𝑡) = 0 ⇒ 𝐸𝐼
𝜕2
𝜕𝑥2 𝑣( 𝑙, 𝑡) = 0
𝑄( 𝑙, 𝑡) = 0 ⇒ 𝐸𝐼
𝜕3
𝜕𝑥3 𝑣( 𝑙, 𝑡) = 0
𝑄( 𝑙, 𝑡) = ∓ 𝑘𝑣( 𝑙, 𝑡) ∓ 𝑐
𝜕
𝜕𝑡
𝑣( 𝑥, 𝑡) ∓ 𝑚
𝜕2
𝜕𝑡2 𝑣( 𝑥, 𝑡) ⇒ 𝐸𝐼 𝑦𝑦
𝜕3
𝜕𝑥3 𝑣( 𝑙, 𝑡) = ∓ ⋯
𝑀( 𝑙, 𝑡) = ± 𝑘 𝑇
𝜕
𝜕𝑥
𝑣( 𝑙, 𝑡) ± 𝑐
𝜕
𝜕𝑡
𝜕
𝜕𝑥
𝑣( 𝑥, 𝑡) ± 𝐽 𝑦𝑦
𝜕2
𝜕𝑡2
𝜕
𝜕𝑥
𝑣( 𝑥, 𝑡) ⇒ 𝐸𝐼 𝑦𝑦
𝜕2
𝜕𝑥2 𝑣( 𝑙, 𝑡) = ± ⋯
𝑥
𝑣(𝑥, 𝑡)
𝑥
𝑣(𝑥, 𝑡)

60. 60
3.6- Metodo Aproximado da Energia de Rayleigh
3.6.1 – Glossário
• Função Característica – Soluções do problema característico, associadas a uma frequência natural.
Definem as formas naturais do sistema e respeitam as condições fronteira e geometria do problema e
verificam a EDM.
• Função Teste – Conjunto de funções que respeitam todas as condições de fronteira (Geométricas e
Naturais) e que são deriváveis pelo menos um número de vezes igual a metade da ordem do sistema. Não
verificam necessariamente a EDM
• Função Admissível – Conjunto de funções que respeitam apenas as condições de fronteira geométricas e
que são deriváveis pelo menos o numero de vezes correspondente a metade da odem do sistema. Não
verificam necessariamente a EDM
• Quociente de Rayleigh – Obtido pela integração da equação diferencial do problema característico (análise
energética), que permite calcular um máximo para a frequência fundamental a partir de uma função de
aproximação que:
o Baseado na consevação da energia mecânicaEnergia potencial máxima e Energia cinética máxima:
𝑇 𝑚𝑎𝑥 = 𝑉𝑚 𝑎𝑥
o O quociente de Rayleigh, quando avaliado para uma determianda função 𝜑(𝑥) apresenta um
valor estacionáio na vizinhança das frequências naturais do sistema
o Na vizinhança da frequência natural fundamental apresenta um valor estacionário mínimo, isto é,
é um Majorante da Frequência natural fundamental
o Processo Convergente: Se função de aproximação diferir de uma pequena quantidade de 1ªordem
da função característica 𝑈 𝑛(𝑥) , então o Quociente de Rayleigh difere de uma quantidade de 2ª
ordem do quadrado da frequência natural 𝑖 , 𝜔𝑖
2
. A frequência estimada apresenta sempre
menor erro que a função de aproximação usada. Usado como acelerador de convergência em
processos iterativos
o Quando a função admissível coincide com a forma natural para uma dada frequência natural, o
quociente de Rayleigh resulta na próprio frequencia natural (erro nulo)
o Não há necessidade de resolver a equação característica
o Fisicamente a frequência estimada é sempre superior à frequencia fundamental uma vez que a
função aproximação introduz uma configuração não natural e por isso introduz restrições ao
movimento do sistema. Aumentando assim a rigidez do sistema.
• Formulação Forte – Formulação que admite que as funções de aproximação são funções de teste.
• Formulação fraca – Derivação de uma nova expressão que substitua a expressão de aporximação de
Rayleigh, e especialmente para a qual se verifique um relaxamento das condições de fronteira.

61. 61
3.6.2 – Procedimento
• Arbitar uma Função Admissível:
o Função admissível para problemas de 2ª ordem (deformação axial de barras, torção de veios)
𝛷( 𝑥) = 𝑎𝑥 + 𝑏
o Função admissível para problemas de 4ª ordem (flexão de vigas)
𝛹( 𝑥) = 𝑎𝑥2
+ 𝑏𝑥 + 𝑐
• Respeito pelas Condições Fronteira Geométricas
o Problemas de 2ª ordem (deformação axial de barras, torção de veios)
𝛷( 𝑙) = 0 ⇒ 𝑎(𝑙) + 𝑏 = 0
o Problemas de 4ª ordem (flexão de vigas)
𝛹( 𝑙) = 0 ⇒ 𝑎(𝑙)2
+ 𝑏(𝑙) + 𝑐
𝜕
𝜕𝑥
𝛹( 𝑙) = 0 ⇒ 2𝑎(𝑙) + 𝑏 = 0
• ( Adequabilidade da Função de aproximação do ponto de vista Físico )
– Traçar o gráfico da função aproximação e visualisar se esse movimento é
compatível com as condições fronteira, e se não é movimento de corpo rígido
(nenhum ponto com deslocamento nulo)
• Calcular o quociente de Rayleigh
o 𝜔 𝑅
2
=
𝑉 𝑚𝑎𝑥
𝑇∗
• Optimizar os parâmetros da função de aproximação
o
𝜕
𝜕𝛿
( 𝜔 𝑅
2) = 0 , procurar a função que introduz menor rigidez possível
Energia cinética de Referência
(sem a dependência do tempo)

62. 62
Elemento Linear
Energia Barra Veio Viga
𝑉𝑚𝑎𝑥
1
2
∫ 𝐴𝐸 [
𝜕
𝜕𝑥
𝛷( 𝑥)]
2
𝑑𝑥
𝑙
0
+ 𝑉𝑐𝑓𝑛
1
2
∫ 𝐺𝐼 𝑝 [
𝜕
𝜕𝑥
𝛷( 𝑥)]
2
𝑑𝑥
𝑙
0
+ 𝑉𝑐𝑓𝑛
1
2
∫ 𝐸𝐼 [
𝜕2
𝜕𝑥2
𝛷( 𝑥)]
2
𝑑𝑥
𝑙
0
+ 𝑉𝑐𝑓𝑛
𝑉𝑐𝑓𝑛 𝑉𝑐𝑓𝑛 =
𝑘
2
[ 𝛷( 𝑥)|𝑥= ]
2
𝑉𝑐𝑓𝑛 =
𝑘 𝑇
2
[ 𝛷( 𝑥)|𝑥= ]
2
𝑉𝑐𝑓𝑛 =
𝑘
2
[ 𝛷( 𝑥)|𝑥=]
2
+
𝑘 𝑇
2
[
𝜕
𝜕𝑥
𝛷( 𝑥)|𝑥=]
2
𝑇∗
1
2
∫ 𝜌𝐴 [ 𝛷( 𝑥)]2
𝑑𝑥
𝑙
0
+ 𝑇𝑐𝑓𝑛
1
2
∫ 𝜌𝐼 𝑝 [ 𝛷( 𝑥)]2
𝑑𝑥
𝑙
0
+ 𝑇𝑐𝑓𝑛
1
2
∫ 𝜌𝐴 [ 𝛷( 𝑥)]2
𝑑𝑥
𝑙
0
+ 𝑇𝑐𝑓𝑛
𝑇𝑐𝑓𝑛 𝑚 𝑝𝑒𝑠𝑜[ 𝛷( 𝑥)|𝑥= ]
2
𝐽 𝑣𝑜𝑙𝑎𝑛𝑡𝑒 [ 𝛷( 𝑥)|𝑥= ]
2
𝑚 𝑝𝑒𝑠𝑜[ 𝛷( 𝑥)|𝑥= ]
2
+
𝐼 𝑦𝑦 𝑖𝑛é𝑟𝑐𝑖𝑎
2
[
𝜕
𝜕𝑥
𝛷( 𝑥)|𝑥= ]
2

63. 63
3.7 – Considerações Práticas – Casos Particulares
3.7.1- Resolução Analítica do Problema Característico
• Variação de Secção
- Criação de n funções de deslocamento: 𝑢1( 𝑥1, 𝑡) 𝑒 𝑢2( 𝑥2, 𝑡) com referenciais distintos
- EDM:
𝜕
𝜕𝑥
(𝑘(𝑥)
𝜕
𝜕𝑥
𝑢1(𝑥1, 𝑡)) =
𝜕2
𝜕𝑡2 𝑢1(𝑥1, 𝑡)
𝜕
𝜕𝑥
(𝑘(𝑥)
𝜕
𝜕𝑥
𝑢2(𝑥2, 𝑡)) =
𝜕2
𝜕𝑡2 𝑢2(𝑥2, 𝑡)
- Funcoes caracteristicas: 𝑢 𝑛( 𝑥, 𝑡) {
𝐴1 cos (
𝜔 𝑛
𝑐
𝑥) + 𝐵1 sin(
𝜔 𝑛
𝑐
𝑥) 𝑝𝑎𝑟𝑎 𝑥 <
𝑙
2
𝐴2 cos (
𝜔 𝑛
𝑐
𝑥2) + 𝐵2 sin(
𝜔 𝑛
𝑐
𝑥2) 𝑝𝑎𝑟𝑎 𝑥2 <
𝑙
2
- Condições Fronteira
Veios, barras:
𝑢1(0, 𝑡) =. .. (condição fronteira 𝑥 = 0 , 1x)
𝑢1 (
𝑙
2
, 𝑡) = 𝑢2(0, 𝑡) (igualdade de deslocamento)
𝜕
𝜕𝑥
(𝑘(𝑥)
𝜕
𝜕𝑥
𝑢1( 𝑥, 𝑡)|
𝑥=
𝑙
2
) =
𝜕
𝜕𝑥
(𝑘(𝑥)
𝜕
𝜕𝑥
𝑢2( 𝑥, 𝑡)| 𝑥2=0
) (igualdade de esforço interno)
𝑢2 (
𝑙
2
, 𝑡) = ⋯ (condição fronteira 𝑥 = 𝑙 , 1x)
Vigas:
𝑣1(0, 𝑡) =. .. 𝑣1(0, 𝑡) =. .. (condições fronteira 𝑥 = 0 , 2x)
𝑣1 (
𝑙
2
, 𝑡) = 𝑣2(0, 𝑡) (igualdade de deslocamento)
𝜕
𝜕𝑥
𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
=
𝜕
𝜕𝑥
𝑣2( 𝑥, 𝑡)| 𝑥2=0
(igualdade de rotações)
𝜕
𝜕𝑥
(𝐸𝐼
𝜕
𝜕𝑥2 𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
) =
𝜕
𝜕𝑥
(𝐸𝐼
𝜕
𝜕𝑥2 𝑣2( 𝑥, 𝑡)| 𝑥2=0
) (igualdade de esforço transverso)
𝐸𝐼
𝜕2
𝜕𝑥2 𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
= 𝐸𝐼
𝜕2
𝜕𝑥2 𝑣2( 𝑥, 𝑡)| 𝑥2=0
(igualdade de momento fletor)
𝑣2 (
𝑙
2
, 𝑡) = ⋯ 𝑣2 (
𝑙
2
, 𝑡) =. .. (condições fronteira 𝑥 = 𝑙 , 2x)

64. 64
• Condições Fronteira Naturais a meio vão
- Criação de 2 funções de deslocamento: 𝑢1( 𝑥, 𝑡) 𝑒 𝑢2( 𝑥, 𝑡) ambas com o mesmo referencial x
- EDM
𝜕
𝜕𝑥
(𝑘(𝑥)
𝜕
𝜕𝑥
𝑢1(𝑥, 𝑡)) =
𝜕2
𝜕𝑡2 𝑢1( 𝑥, 𝑡) ;
𝜕
𝜕𝑥
(𝑘(𝑥)
𝜕
𝜕𝑥
𝑢2(𝑥, 𝑡)) =
𝜕2
𝜕𝑡2 𝑢2(𝑥, 𝑡)
- Funcoes caracteristicas: 𝑢 𝑛( 𝑥, 𝑡) {
𝐴1 cos (
𝜔 𝑛
𝑐
𝑥) + 𝐵1 sin (
𝜔 𝑛
𝑐
𝑥) 𝑝𝑎𝑟𝑎 𝑥 <
𝑙
2
𝐴2 cos (
𝜔 𝑛
𝑐
𝑥) + 𝐵2 sin (
𝜔 𝑛
𝑐
𝑥) 𝑝𝑎𝑟𝑎 𝑥2 <
𝑙
2
- Condições Fronteira
Veios, barras:
𝑢1(0, 𝑡) =. .. (condição fronteira 𝑥 = 0 , 1x)
𝑢1 (
𝑙
2
, 𝑡) = 𝑢2(0, 𝑡) (igualdade de deslocamento)
𝜕
𝜕𝑥
(𝑘( 𝑥)
𝜕
𝜕𝑥
𝑢1( 𝑥, 𝑡) |
𝑥=
𝑙
2
) = +
𝜕
𝜕𝑥
(𝑘(𝑥)
𝜕
𝜕𝑥
𝑢2( 𝑥2, 𝑡) | 𝑥=0
) − 𝑘𝑢2(0, 𝑡) − . ..
𝑢2 (
𝑙
2
, 𝑡) = ⋯ (condição fronteira 𝑥 = 𝑙 , 1x)
Vigas:
𝑣1(0, 𝑡) =. .. 𝑣1(0, 𝑡) =. .. (condições fronteira 𝑥 = 0 , 2x)
𝑣1 (
𝑙
2
, 𝑡) = 𝑣2(0, 𝑡) (igualdade de deslocamento)
𝜕
𝜕𝑥
𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
=
𝜕
𝜕𝑥
𝑣2( 𝑥, 𝑡)| 𝑥2=0
(igualdade de rotações)
𝜕
𝜕𝑥
(𝐸𝐼
𝜕
𝜕𝑥2 𝑣1( 𝑥, 𝑡) |
𝑥=
𝑙
2
) = +
𝜕
𝜕𝑥
(𝐸𝐼
𝜕
𝜕𝑥2 𝑣2( 𝑥, 𝑡) | 𝑥2=0
) + 𝑘𝑣2(0, 𝑡)+. ..
𝐸𝐼
𝜕2
𝜕𝑥2 𝑣1( 𝑥, 𝑡) |
𝑥=
𝑙
2
= 𝐸𝐼
𝜕2
𝜕𝑥2 𝑣2( 𝑥, 𝑡) | 𝑥2=0
(igualdade de Momento Fletor)
𝑣2 (
𝑙
2
, 𝑡) =. .. 𝑣2 (
𝑙
2
, 𝑡) =. .. (condições fronteira 𝑥 = 𝑙 , 2x)

65. 65
Vigas:
𝑣1(0, 𝑡) =. .. 𝑣1(0, 𝑡) =. .. (condições fronteira 𝑥 = 0 , 2x)
𝑣1 (
𝑙
2
, 𝑡) = 𝑣2 (
𝑙
2
, 𝑡) (igualdade de deslocamento)
𝜕
𝜕𝑥
𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
=
𝜕
𝜕𝑥
𝑣2( 𝑥, 𝑡)| 𝑥2=0
(igualdade de rotações)
𝜕
𝜕𝑥
(𝐸𝐼
𝜕
𝜕𝑥2 𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
) =
𝜕
𝜕𝑥
(𝐸𝐼
𝜕
𝜕𝑥2 𝑣2( 𝑥, 𝑡)| 𝑥2=0
) (igualdade de esforço Transv.)
𝐸𝐼
𝜕2
𝜕𝑥2 𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
= +𝐸𝐼
𝜕2
𝜕𝑥2 𝑣2( 𝑥, 𝑡)| 𝑥2=0
− 𝑘𝑣2(0, 𝑡)−. …
𝑣2 (
𝑙
2
, 𝑡) =. .. 𝑣2 (
𝑙
2
, 𝑡) =. .. (condições fronteira 𝑥 = 𝑙 , 2x)

66. 66
• Condições Fronteira Geométricas a meio vão ( Vigas )
Vigas:
𝑣1(0, 𝑡) =. .. 𝑣1(0, 𝑡) =. .. (condições fronteira 𝑥 = 0 , 2x)
𝑣1 (
𝑙
2
, 𝑡) = 0
𝑣2(0, 𝑡) = 0
𝜕
𝜕𝑥
𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
=
𝜕
𝜕𝑥
𝑣2( 𝑥, 𝑡)| 𝑥2=0
(igualdade de rotações)
𝐸𝐼
𝜕2
𝜕𝑥2 𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
= 𝐸𝐼
𝜕2
𝜕𝑥2 𝑣2( 𝑥, 𝑡)| 𝑥2=0
(igualdade de Momento Fletor)
𝑣2 (
𝑙
2
, 𝑡) = ⋯ 𝑣2 (
𝑙
2
, 𝑡) =. .. (condições fronteira 𝑥 = 𝑙 , 2x)
Vigas:
𝑣1(0, 𝑡) =. .. 𝑣1(0, 𝑡) =. .. (condições fronteira 𝑥 = 0 , 2x)
𝑣1 (
𝑙
2
, 𝑡) = 𝑣2 (
𝑙
2
, 𝑡) (igualdade de deslocamento)
𝜕
𝜕𝑥
𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
= 0
𝜕
𝜕𝑥
𝑣2( 𝑥, 𝑡)| 𝑥2=0
= 0
𝜕
𝜕𝑥
(𝐸𝐼
𝜕
𝜕𝑥2 𝑣1( 𝑥, 𝑡)|
𝑥=
𝑙
2
) =
𝜕
𝜕𝑥
(𝐸𝐼
𝜕
𝜕𝑥2 𝑣2( 𝑥, 𝑡)| 𝑥2=0
) (igualdade de esforço Transv.)
𝑣2 (
𝑙
2
, 𝑡) = ⋯ 𝑣2 (
𝑙
2
, 𝑡) =. .. (condições fronteira 𝑥 = 𝑙 , 2x)

67. 67
3.7.2- Método de Rayleigh
• Variação de Secção
𝑉𝑚𝑎𝑥 =
1
2
∫ 𝐴1 𝐸1 [
𝜕
𝜕𝑥
𝛷( 𝑥)]
2
𝑑𝑥
𝑙1
0
+
1
2
∫ 𝐴2 𝐸2 [
𝜕
𝜕𝑥
𝛷( 𝑥)]
2
𝑑𝑥
𝑙2
𝑙1
+. . . +𝑉𝑐𝑓𝑛
𝑇∗
=
1
2
∫ 𝜌1 𝐴1 [ 𝛷( 𝑥)]2
𝑑𝑥
𝑙1
0
+
1
2
∫ 𝜌2 𝐴2 [ 𝛷( 𝑥)]2
𝑑𝑥
𝑙2
𝑙1
+. . . +𝑇𝑐𝑓𝑛
• Condições Fronteira a meio vão
- Função aproximação com significado físico na posição da C.F a meio vão
(deslocamento máximo para C.F. fixo-fixo; nodo de vibração para livre-
livre
- Calcular 𝑉𝑐𝑓𝑛 𝑒 𝑇𝑐𝑓𝑛 para a C.F a meio vão

68. 68
4 - Controlo de Vibrações
Diagrama de Controlo de Vibrações
• Controlo Activo Malha Fechada (w/ Feedback)
Malha Aberta (no Feeedback)
• Semi Activo
• Controlo Passivo
o Isolamento de Vibrações ( Vibration Isolation source/receiver )
Isolamento da Vibração por aumento da massa do sistema
Rubbber plates
Isolamento da Vibração por diminuição da rigidez da ligação à fundação
Air-spring isolation

69. 69
o Absorsor de Vibrações (Tuned Mass Dampers - TMD)
Modelo de absorsor de
vibrações (massa-mola-
amortecedor)
Absorsor de Vibrações sísmicas usado em arranha-céus
(modelo com pêndulo simples)
Taipei skyscraper

70. 70
o Manutenção de Equipamentos (Maintenance calibration)
Balancing turbine bladesModelo massas
rotativas
desiquilibradas
Reparing broken
fan blades