1) O documento apresenta a resolução de dois problemas envolvendo cálculos de campos de velocidade e fluxo. O primeiro problema calcula a velocidade em diferentes regiões de um campo de escoamento dado. O segundo problema calcula a vazão volumétrica e o fluxo de quantidade de movimento através de uma superfície inclinada para um campo de velocidade dado.

![Determine:
(a) O centro de massa yc como função do nível h.
(b) O nível para a menor tendência de tombamento da lata.
(c) O coeficiente mínimo de atrito estático, µs, para o qual a lata cheia tombaria sem deslizamento.
(d) O gráfico de µs)mínimo para inclinar (não deslizar) a lata como função do nível de líquido na lata.
Solução:
M SG
g
cm
mL
cm
mL
g máx
h
A D
mL
cm
cm
mL
mm
cm
mm
Em qualquer nível m
h
h
M m g
h mm
mm
g h mm
b b
máx
b b
b
máx
b b
ϭ ϭ ϫ ϫ ϫ ϭ
ϭ ϭ ϫ ϫ ϫ ϫ ϫ ϭ
ϭ ϭ ϫ ϭ
∀
∀ ∀
1 05 1 0 354 372
4 4
354
1
6 5
10 107
107
372 3 47
3
3
2 2 2
3
, , ( )
( , )
, ; ( )
( )
, ( )
Das considerações de quantidade de movimento,
y M
h
m
H
m h h h
M m m h
y
h
h
h em mm y
c b c
b
c c
ϭ ϩ ϭ ϩ ϭ ϩ
ϭ ϩ ϭ ϩ
ϭ
ϩ
ϩ
2 2
1
2
3 47 120 20
1
2
3 47 2400
3 47 20
3 47 2400
6 94 40
2
2
( , ) ( ) ( , )
,
,
,
( )
[ ]
←
l
A tendência para tombar será menor quando yc for mínimo. Portanto,
dy
dh
h
h
h
h
h h
h
c
ϭ
ϩ
ϩ Ϫ
ϩ
ϩ
ϭ
ϩ Ϫ
ϩ
ϭ
2 3 47
6 94 40
1 6 95
3 47 2400
6 94 40
24 1 278 16 700
6 94 40
0
2
2
2
2
( , )
,
( )( , )
,
( , )
, .
( , )
Usando a fórmula quadrática,
h para y mín mm
h
y mínc c
( )
( ) ( , ) ,
( , )
, ( )ϭ
Ϫ Ϯ ϩ
ϭ
278 278 4 24 1 16 700
2 24 1
21 2
2
←
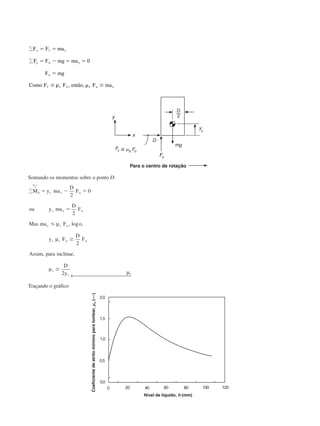
Traçando o gráfico
Trace um diagrama de corpo livre da lata para tombamento iminente
AlturadoCG,yc(mm)
Nível de líquido, h (mm)
CAP004/1 11/8/02, 9:41 AM2](https://image.slidesharecdn.com/capitulo4-160329182248/85/Solucionario-Capitulo4-FOX-2-320.jpg)

![Solução:
( ) ( ˆ ˆ) ( ˆ)
( )
a V dA az j b k wdzj awz dz V dA
b V dA awz dz aw
z
aw
z
V dA
z
A
z
A
r r r r
r r r r
и ϭ ϩ и Ϫ ϭϪ и
и ϭ Ϫ ϭϪ ϭϪ и
1
1
01
2
0
1
2
1
1 1
1 12 2
←
∫
←
∫∫
←
←
( ) ( ˆ ˆ) ( ˆ)
( ) ( ) ( ˆ ˆ)( ) ˆ ˆ ( )
c V dA azj bk wdyk bwdy
V dA
d V V dA azj bk bwdy abwzdy j b wdy k
V V dA
r r
r r
r r r
r r r
и ϭ ϩ и Ϫ ϭϪ
и
и ϭ ϩ Ϫ ϭϪ Ϫ
и
2
2
2
1
2
←
∫∫ ∫
∫
( ) ( ) ( ˆ ˆ) ˆ,
. ,
( ) , ˆ ( )
s
ˆ ˆ / ( )
e V V dA abwz dz j b wdy k b wdy k
pois z ao longo de A Dessa forma
V V dA b wy k
m
w m k w k m s e
y
A
y
A
x
r r r
r r r
и ϭ Ϫ Ϫ ϭϪ
ϭ
и ϭϪ ϭϪ ϫ ϭϪ
2
02
2 2
0
1
2
2
2
2 2
2
2
3 2
1
0
5 1 25
Problema 4.13
Dado: Um campo de escoamento dado por
r
V ayi bjϭ ϩˆ ˆ
onde a ϭ 2 sϪ1
, b ϭ 1 ft/s e as dimensões são em pés.
Determine: (a) Vazão volumétrica.
(b) Fluxo de quantidade de movimento através da superfície inclinada.
Solução:
A vazão volumétrica é Q V dAϭ и
r r
∫
Para a superfície inclinada
dA dA ı dA j c dyı c dxj
onde c ft
Q ayı bj cdyı cdxj acy dy bcdx
Q ac y bcx ft
ft
ft ft
Q ft s Vazão volumétrica
x y
A y o x
r
ϭ ϩ ϭ ϩ
ϭ
ϭ ϩ и ϩ ϭ ϩ
ϭ ϩ ϭ ϫ ϫ ϩ ϫ
ϭ
ϭ ϭ
Ϫ
ˆ ˆ ˆ ˆ
( ˆ ˆ) ( ˆ ˆ)
/
2
25 2 1
2
2 3
8
1
0
3
2
2 0
1
0
3 1
2
3
∫ ∫ ∫
] ]
←
CAP004/1 11/8/02, 9:41 AM5](https://image.slidesharecdn.com/capitulo4-160329182248/85/Solucionario-Capitulo4-FOX-5-320.jpg)
![O fluxo de quantidade de movimento é dado por
f m V V dA. . ( )ϭ и
r r
∫
Então,
f m ayı bj acy dy bc dx
f m ı a cy dy abcy dx j abcy dy b cdx
Ao longo da erfície inclinada y
x
f m ı a c y abc
x
A
. . ( ˆ ˆ) ( )
. . ˆ ˆ
sup
. . ˆ
ϭ ϩ ϩ
ϭ ϩ ϩ ϩ
ϭϪ ϩ
ϭ ϩ Ϫ ϩ
∫
∫ ∫ ∫∫
]
0
1
2 2
0
3
2
0
3
0
1
2 3
3 0
1
3
1
3
11
2 2
3
2 2
2
1 2 3
0
3
2
2 0
1 2
0
3
1 2
3 2
0
3
1
2 2
2
] ]{ }
∫ dx j abc y b cx
ı s ft
ft
abc
x
b
x j s
ft
s
ft
ft ft
s
ft ft
ϩ ϩ
ϭ ϫ ϫ ϩ Ϫ ϩ ϩ ϫ ϫ ϩ ϫ ϫϪ Ϫ
ˆ
ˆ ( ) ˆ
{ } ←
ϭ ϩ ϫ ϫ ϫ ϩ ϩ
ϭ ϩ
Ϫ
ˆ , ˆ
. . , ˆ ˆ
ı
ft
s
s
ft
s
ft ft j
ft
s
ft
s
f m ı j
ft
s
Fluxo da quantidade de movimento
8
3
2 2 2 5 2 6
7 67 8
4
2
1 2
4
2
4
2
4
2
Notas: As unidades de massa específica são slug/ft3
.
O fluxo de quantidade de movimento tem unidades slug.
ft/s2
(ou lbf).
Problema 4.19
Dados: Escoamento permanente e incompressível através do dispositivo mostrado.
A m A m A m
V ı m s V j m s
1
2
2
2
3
2
1 2
0 05 0 01 0 06
4 8
ϭ ϭ ϭ
ϭ ϭ Ϫ
, , , , ,
ˆ / , ˆ /
r r
Determine: A velocidade
r
V3.
Solução: Aplique a conservação de massa usando o VC mostrado.
Equação básica:
ϭ
ϭ ϩ и
0 1
0
( )
∂
∂
∀∫ ∫t VC SC
d V dA
r r
CAP004/1 11/8/02, 9:41 AM6](https://image.slidesharecdn.com/capitulo4-160329182248/85/Solucionario-Capitulo4-FOX-6-320.jpg)









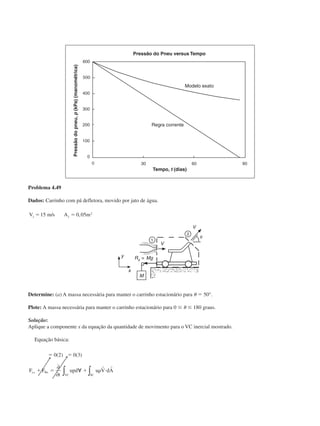
![Problema 4.41
Dados: Tanque contendo salmoura com corrente de entrada de água em regime permanente. A massa específica inicial é
i Ͼ H O2
.
Determine: (a) A taxa de variação da massa específica do líquido no tanque.
(b) O tempo requerido para atingir a massa específica, f, onde i fϾ Ͼ H O2
.
Solução: Aplique a conservação de massa, usando o VC mostrado.
Equação básica:
0 ϭ ϩ и 〈
∂
∂
∀∫ ∫t
d V d
VC SC
r r
Considerações: (1) ᭙tanque ϭ constante.
(2) Massa específica uniforme no tanque.
(3) Escoamento uniforme nas seções de entrada e de saída.
Então, V1A1 ϭ V2A2, posto que o volume do tanque é constante e
0 2 2 2
ϭ ϩ Ϫ ϭ ϩ Ϫ ϭ
ϩ Ϫ
∂
∂
∫ ∀
∂
∂
∀ ∀
t
d VA VA
t
VA
d
dt
VAvc H O H O H O ( ) ( )
E daí
d
dt
VA
d
dtH O
ϭ Ϫ
Ϫ
᭙
( )
2
←
Separando variáveis,
d VA
dt
H O
Ϫ
ϭϪ
2
∀
Integrando de i em t ϭ 0 até f em t,
d VA
dt
VA
t
H O
H O
f H O
i H O
t
i
f
i
f
Ϫ
ϭ Ϫ ϭ
Ϫ
Ϫ
ϭ Ϫ ϭϪ
2
2
2
2
0∫ ∫]
∀ ∀
ln ( ) ln
Finalmente,
t
VA t
f H O
i H O
ϭϪ
Ϫ
Ϫ
∀
←
ln
2
2
{Note que f → H O2
assintoticamente quando t → ϱ.}
entra
constante
sai
CAP004/2 11/4/02, 2:28 PM16](https://image.slidesharecdn.com/capitulo4-160329182248/85/Solucionario-Capitulo4-FOX-16-320.jpg)




![Na seção ባ,
r r
V.dA VRtdϭ , visto que o fluxo é para fora do VC. Então,
Q VRtd VRt VRt
Q
m
s
m m m s Qs
ϭ ϭ ϭ
ϭ ϫ ϫ ϫ ϭ
Ϫ
Ϫ
[ ]
←
∫ /
/
/
/
, , , /
2
2
2
2
15 0 3 0 03 0 424
Da quantidade de movimento
R V dA V dA V dA
com V
R V VRtd V Rt sen V Rt
R
kg
m
m
s
m
y
SC A A
y
y
ϭ и ϭ Ϫ ϩ ϩ
ϭ ϭ
ϭ ϭ ϭ
ϭ ϫ ϫ ϫ ϫ
Ϫ
Ϫ
∫ ∫ ∫
∫
{ } { }
[ ]
v v v
v
r r
1 2
1 1 1 2 2 2
1 2
2
2
2
2
2 2
3
2
2
2
0
2
2 999 15 0 3 0
cos
cos
( ) ,
/
/
/
/
,, ,03 4 05
2
m
N s
kg m
KN Ryϫ
и
и
ϭ ←
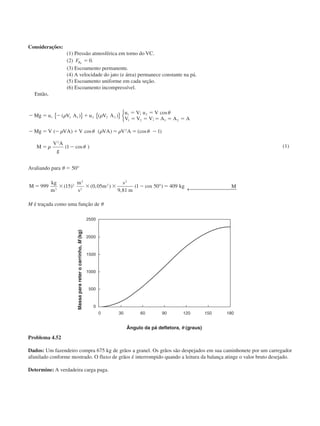
Problema 4.61
Dados: Motor a jato em banco de ensaio. O combustível entra verticalmente a uma vazão ˙ ˙ , ˙ .m mf ϭ ϭmcombustível ar0 02
Determine: (a) A vazão mássica de ar.
(b) Estime o empuxo do motor.
Solução: Aplique a componente x da equação da quantidade de movimento ao VC mostrado.
Equações básicas:
ϭ ϭ
ϩ ϭ ϩ и
ϭ ϭ
0 1 0 2
1 1 1
( ) ( )
˙ , /
F F
t
u d u V dA
m V A p RT
S B
SCVC
ar
x x
∂
∂
∀ ∫∫
r r
Considerações:
(1) FBx
ϭ 0.
(2) Escoamento permanente.
(3) Escoamento uniforme nas seções de entrada e de saída.
(4) O ar comporta-se como gás ideal, T ϭ 70°F.
(5) O combustível entra verticalmente (dado).
CAP004/2 11/4/02, 2:28 PM24](https://image.slidesharecdn.com/capitulo4-160329182248/85/Solucionario-Capitulo4-FOX-24-320.jpg)

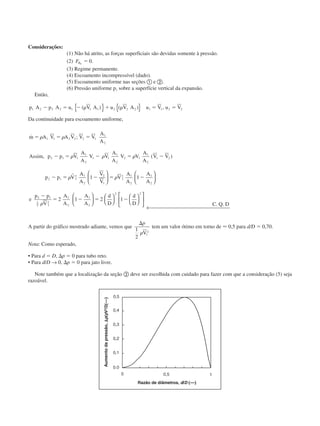

![ϭ ϫ ϩ Ϫ ϫ
и
и
Ϫ ϭ Ϫ
999
1
0 075
3 0 0 065 30 0 01 6 6 0 075
84 2
3 2
2 2 2
2
2
2
2
2 1 2 1
kg
m m
m
s
m
N s
kg m
p p kPa p p
,
( , ) ( , ) ( ) ( , ) ( , ) ( , )
,
[ ]
←
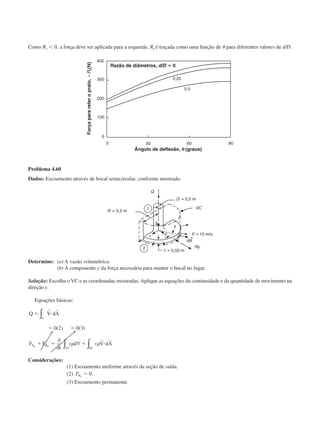
Problema 4.69
Dados: Cotovelo redutor conforme mostrado. O fluido é água.
Determine: As componentes da força necessária para manter o cotovelo no lugar.
Solução: Aplique as componentes x e y da equação da quantidade de movimento usando a SC e o CV mostrados.
Equações básicas:
ϭ ϭ
ϩ ϭ ϩ и
ϭ
ϩ ϭ ϩ и
0 4 0 1
0 1
( ) ( )
( )
F F
t
u d u V dA
F F
t
d V dA
S B
SCVC
S B
SCVC
x x
y y
∂
∂
∀
∂
∂
∀
∫∫
∫∫
r r
r r
v v
Considerações:
(1) Escoamento permanente.
(2) Escoamento uniforme em cada seção.
(3) Use pressões manométricas.
(4) Eixo x horizontal.
Componente segundo x:
R p A p A u Q u Q
u V u V
R V V Q p A p A V
Q
A
m
s m
m
s
m
s
m
s
x g g
x g g
ϩ Ϫ ϭ Ϫ ϩ ϩ
ϭ ϭ
ϭ Ϫ ϩ Ϫ ϩ ϭ ϭ ϫ ϭ
ϭ Ϫ ϩ ϫ
1 1 2 2 1 2
1 1 2 2
1 2 1 1 2 2 1
1
3
2
0 11
1
0 0182
6 04
6 04 13 6 30
cos
cos
( cos ) cos ,
,
,
( , , cos
{ } { }
°°
°
←
) ,
,
,
, ( ) , ( ) , cos
999 0 11
1
0 0082
13 6
0 11 200 101 10 0 0182 120 101 10 0 0081 30
631 1800 133 1040
2 2
2
3
2
3 2
3
2
2 3
2
2
kg
m
V
Q
A
m
s m
m
s
m
s
N s
kg m
N
m
m
N
m
m
R N N R
x
x x
ϭ ϭ ϫ ϭ
ϫ ϫ
и
и
Ϫ Ϫ ϫ ϩ Ϫ ϫ ϫ
ϭϩ Ϫ ϩ ϭϪ
Massa do cotovelo, m ϭ 10 kg
Volume interno V ϭ 0,006 m3
CAP004/2 11/4/02, 2:28 PM28](https://image.slidesharecdn.com/capitulo4-160329182248/85/Solucionario-Capitulo4-FOX-28-320.jpg)





![Então,
0 1 2
2 1 2
1
2
1
4
1
2
0
2
1
2 2
21
2
2 4
0
1
ϭ Ϫ ϩ Ϫ
ϭ Ϫ ϭ Ϫ
U R u
r
R
rdr
ou U R u R
r
R
r
R
d
r
R
u R
r
R
r
R
máx
R
máx
o
máx
{ }
∫
∫
AssimAssim u U
ft
ft s umáx máx, /ϭ ϭ ϫ ϭ2 2 30
3
601 ←
Da equação da quantidade de movimento,
p R p R u U R u u dA U R u R
r
R
r
R
d
r
R
u U u u
r
R
ou
p p U
R
máx
máx
1
2
2
2
1 1
2
2 2
0
2 1
2 2 2
2
0
1
1 1 2
2
1 2
2 1
1
Ϫ ϭ Ϫ ϩ ϭ Ϫ ϩ Ϫ
ϭ ϭ Ϫ
Ϫ ϭ Ϫ
{ }
∫ ∫
11
2 2 2 2
0
1
2
0
1
2 4 2
0
1
4 6
0
1
2
1
2
1
2
1 2 1
2
1
2
2 1
1 1 2
1
2
1
2
1
6
1
6
2 4
8
6
ϩ Ϫ ϭ
Ϫ ϭ Ϫ ϩ ϭ Ϫ ϩ ϭ
ϭ ϭ
Ϫ ϭ Ϫ ϩ ϭ
u d
r
R
Mas d d
e u U U
p p U U U
máx
máx
( ) ;
( ) ( )
( ) ,
∫
∫ ∫ ]
logo,
11
2
1
2
2
2
2
2
1 2
2
4
3
1
1
3
1
3
0 075 30
32 2
0 699 1 2
Ϫ ϭ
ϭ ϫ ϫ ϫ ϫ
и
и
Ϫ ϭ Ϫ
µ
←
U
lbm
ft
ft
s
s g
lbm
lbf s
slug ft
p p lbf ft p p
s
, ( )
/
,
, /
Problema 4.82
Dados: Escoamento incompressível em camada limite, conforme mostrado. O fluido é ar padrão.
Na camada limite:
u
U
y y
o
ϭ
␦
Ϫ
␦
3
2
1
2
3
Fronteira da CL
Largura
CAP004/3 11/4/02, 2:31 PM34](https://image.slidesharecdn.com/capitulo4-160329182248/85/Solucionario-Capitulo4-FOX-34-320.jpg)
![Determine: A força horizontal por unidade de largura para manter a placa estacionária.
Solução: Aplique a continuidade e a componente x da equação da quantidade de movimento.
Equações básicas:
ϭ
ϭ ϩ
ϭ ϭ
ϩ ϭ ϩ и
0 1
0
0 3 0 1
( )
( ) ( )
∂
∂
∀
∂
∂
∀
∫ ∫
∫∫
t
d VdA
F F
t
u d u V dA
VC SC
S B
SCVC
x x
r r
r r
Considerações: (1) Escoamento permanente.
(2) Não existe força líquida de pressão;
(3) FBx
ϭ 0.
(4) Escoamento uniforme na seção ab.
(5) Escoamento incompressível.
Então, da equação da continuidade,
0 ϭ Ϫ ϩ ϩ ϭ ϭ Ϫ
␦ ␦␦
␦ ␦U m u dy dy m U u dyo bc
o
bc o
oo
{ }
∫ ∫∫˙ ; ; ˙ ( )
Da equação da quantidade de movimento,
Ϫ ϭ Ϫ ϩ ϩ ϭ Ϫ ϩ ϩ Ϫ
␦
F U U w U m u uwdy U u U U u wdyf o o o bc
o
o o o
o
␦
␦
{ }
[ ]∫ ∫˙ ( )2 2
Força de arrasto ϭ F u U u wdy U
u
U
u
U
wdyf o
o o o o
ϭ Ϫ ϭ Ϫ
␦
␦
( )∫ ∫
0
2
1
Na seção cd,
u
U
dy d
F
w
U
u
U
u
U
d U d
U
o
f
o
o o o
o
o
o
ϭ Ϫ ϭ ␦
ϭ ␦ Ϫ ϭ ␦ Ϫ Ϫ ϩ
ϭ ␦ Ϫ Ϫ ϩ Ϫ
ϭ
3
2
1
2
1
3
2
1
2
1
3
2
1
2
3
2
9
4
1
2
3
2
1
4
3
2
1
2 3 3
1
2 2 3 4 6
;
∫ ∫
←
∫ d
U U
kg
m
m
s
m
N s
kg m
F
w
N m para a
F
w
o
o
o
o
f f
ϭ ␦ Ϫ Ϫ ϩ Ϫ ϭ ␦
ϭ ϫ ϫ ϫ ϫ
и
и
ϭ
1
2 2 3 4 5 7
1
2
3
2
2
2
2
3
4
3
4
1
8
3
10
1
28
0 139
0 139 1 23 10 0 0023
0 0393
( , )
, , ( ) ,
, / ( )direita
CAP004/3 11/4/02, 2:32 PM35](https://image.slidesharecdn.com/capitulo4-160329182248/85/Solucionario-Capitulo4-FOX-35-320.jpg)
![Problema 4.83
Enunciado: Considere o jato de água e a placa vertical do Problema-Exemplo 4.4. Uma consideração implícita feita para
resolver o problema foi que o jato permanecesse horizontal até atingir a placa. Discuta as implicações de se incluir a gravida-
de na solução. Concentre-se especificamente na trajetória do jato antes de ele atingir a placa e na velocidade do líquido sobre
a placa acima e abaixo do ponto de impacto do jato. As dimensões da placa vertical são importantes? As propriedades da
corrente de líquido são importantes?
Discussão: A gravidade poderia ser incluída na solução com relativa facilidade. A gravidade produziria uma componente
vertical para baixo na velocidade da corrente de água no jato. O jato teria uma trajetória parabólica; a corrente do jato cairia
mais à medida que ela se afastasse do bocal.
Como uma primeira aproximação, o escoamento sobre a placa vertical é suposto ser sem atrito. Portanto, não existe força
de atrito do jato sobre a placa. Uma força de pressão agindo sobre a placa não possui componente vertical. Conseqüentemen-
te, não pode existir força vertical resultante sobre a placa.
O jato líquido dividir-se-á em duas correntes quando atingir a placa. Cada uma das duas correntes terá a mesma velocida-
de do jato, porque não existe força de atrito ao longo da placa para modificar a velocidade do líquido. Entretanto, a corrente
inferior irá carregar mais da metade do escoamento; a corrente superior carregará menos da metade do fluxo. Posto que
nenhuma força vertical age sobre o escoamento, este dividir-se-á de modo a dar às duas correntes a mesma quantidade de
movimento do jato tocando a placa.
A placa vertical deve ser larga o bastante para redirecionar todo o escoamento do jato de forma que ele saia paralelo à
superfície da placa. Quando a gravidade é incluída, a placa deve estender-se mais para baixo da linha de centro do jato do que
no caso hipotético sem gravidade.
As propriedades da corrente de líquido incluem sua massa específica, área, velocidade e viscosidade. A força horizontal
exercida sobre a placa vertical é proporcional à massa específica, área e ao quadrado da velocidade da corrente líquida. A
viscosidade do líquido não é importante, quando ela é pequena o suficiente para fazer com que a aproximação de um escoa-
mento sem atrito seja um modelo razoável.
Problema 4.87
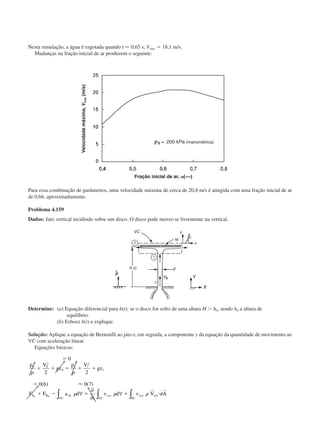
Dados: Modelo de escoamento de gás em um bocal de propulsão como uma fonte esférica; Ve ϭ constante.
Determine: (a) Uma expressão para o empuxo axial, Ta; compare com a aproximação unidimensional, T mVeϭ ˙ .
(b) O erro percentual para ␣ ϭ 15°.
Plote: O erro percentual em função de ␣, para 0 22 5Յ Յ␣ , .°
Solução:
Aplique as definições: ˙ ,m VdA T u Vdaa
A A
ϭ ϭ ∫ ∫
Use escoamento esférico, simétrico.
A vazão mássica é
admitindo
m VdA V Rsen Rd V R V R
e e
e e e e
oA o
e e
␣
␣ ␣
( )
˙ ( ) cos ( cos )
[ ]
[ ]∫∫ϭ ϭ ϭ Ϫ ϭ Ϫ2 2 2 12 2
CAP004/3 11/4/02, 2:32 PM36](https://image.slidesharecdn.com/capitulo4-160329182248/85/Solucionario-Capitulo4-FOX-36-320.jpg)
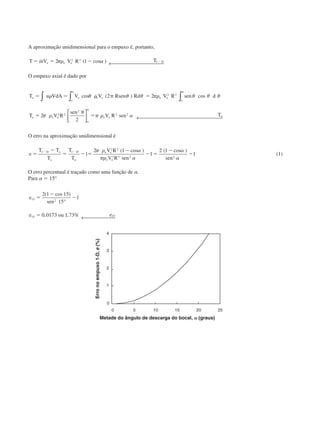





![Da equação de Bernoulli,
ϭ
ϭ Ϫ Ϫ Ϫ ϩ Ϫ ϭ
ϭ ϫ ϫ Ϫ Ϫ ϫ ϫ
и
и
ϭ
0
2
1
2
999 12 2 2 99 999 9 81 0 15 68 4
1 2
2
1
2
1 2 2 1 2
1 2
2 2
2
2 3
1
1
p V V g z z p z z h
p
kg
m
m
s
kg
m
m
s
m
N s
kg m
kPa manométrica p
g g
g
g
( ) ( ) ;
( , ) ( , ) , , , ( )[ ]
←
Calcule V3 na ausência da placa usando Bernoulli (p2 ϭ p3)
V V g H
m
s
m
s
m s3 2
2 2
2
2 2
2 12 2 2 9 81 4 85 15 6
1
2
ϭ ϩ ϭ ϩ ϫ ϫ ϭ( , ) , , , /
Da quantidade de movimento: Rx ϭ 0, posto que não existe atrito na superfície da placa.
Considerações:
(6) Despreze as massas da placa e da água sobre a placa.
(7) Pressão atmosférica age sobre todo o volume de controle; F RS yy
ϭ .
Então,
0 0
15 6 30 999 0 0155 209 209
3 3 4 4 5 5 3 3 3
3
3
R v m v m v m V Q visto que v V
R
m
s
kg
m
m
s
N s
kg m
N K N K
y
y y
y
ϭ Ϫ ϩ ϩ ϩ ϩ ϭ ϭ Ϫ
ϭ ϫ ϫ ϫ ϫ
и
и
ϭ ϭ Ϫ
˙ ˙ ˙ cos , cos
, cos , ,
{ } { } { }
° ←
A pressão é máxima no ponto de estagnação e mínima (patm) em ብ e ቦ. A pressão em a é maior que em b devido à curvatura da
linha de corrente.
CAP004/3 11/4/02, 2:32 PM43](https://image.slidesharecdn.com/capitulo4-160329182248/85/Solucionario-Capitulo4-FOX-43-320.jpg)



![Solução: Aplique a continuidade e a componente x da equação da quantidade de movimento ao VC movendo-se com o prato
como mostrado.
Equações básicas:
ϭ
ϭ ϩ и
ϭ ϭ
ϩ ϭ ϩ и
0 1
0
0 3 0 1
( )
( ) ( )
∂
∂
∀
∂
∂
∀
∫∫
∫ ∫
t
d V dA
F F
t
u d u V dA
xyz
SCVC
B S xyz
VC
xyz
SC
x x
r r
r r
Considerações: (1) Escoamento permanente relativo ao VC.
(2) Nenhuma força resultante de pressão sobre o VC.
(3) Horizontal; FBx
ϭ 0.
(4) Escoamento uniforme em cada seção.
(5) Nenhuma variação na velocidade do jato relativa à pá.
(6) Escoamento incompressível.
Então,
0
4 4
4 4
0 020 0 010 2 36 10
2 2
3 4
3 4
2 2 2 2 2 4 2
ϭ и ϭ Ϫ Ϫ ϩ ϩ
ϭ Ϫ ϭ Ϫ ϭ ϫ Ϫ
r r
V dA V U
D d
A
A D d m m
xyz
SC∫
[ ]
( ) ( )
( ) ( , ) ( , ) ,
,
,
Da equação da quantidade de movimento,
R u V U
D
u V U
d
u V U A
u V U u V U u V U
R V U
D
V U
d
V U
x
x
ϭ Ϫ Ϫ ϩ ϩ Ϫ ϩ ϩ Ϫ
ϭ Ϫ ϭ Ϫ ϭϪ Ϫ
ϭϪ Ϫ ϩ Ϫ Ϫ Ϫ
1
2
2
2
3 3 4
1 2 3
2
2
2
2
2
4 4
40
4 4
( ) ( ) ( )
( ) cos
( ) ( ) ( )
,
{ }
°
4
40
4
1 40
999 30 10 2 36 10 1 40
167
2 2
2 2 2
3
2
2
2
4 2
2
( ) cos
( ) ( ) ( cos )
( ) , ( cos )
( )
D d
V U D d
kg
m
m
s
m
N s
kg m
R N a força deve ser aplicada para a Rx x
Ϫ
ϭϪ Ϫ Ϫ ϩ
ϭϪ ϫ Ϫ ϫ ϫ ϩ ϫ
и
и
ϭϪ
Ϫ
°
°
°
← direita
{Nota: Ry ϭ Mg, pois não há fluxo líquido de quantidade de movimento na direção y.}
CAP004/4 11/6/02, 9:29 AM47](https://image.slidesharecdn.com/capitulo4-160329182248/85/Solucionario-Capitulo4-FOX-47-320.jpg)


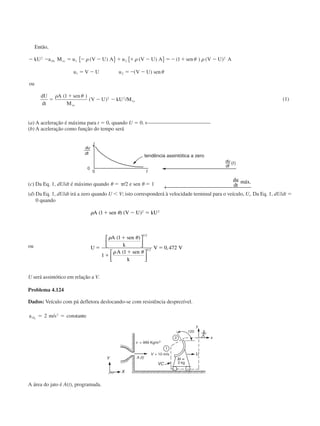

![Problema 4.127
Dados: Foguete trenó desacelerado por concha arrastando água. Arrasto aerodinâmico proporcional a U2
. Para U0 ϭ 300 m/
s, FD ϭ 90 kN. Largura da concha, w ϭ 0,3 m.
Determine: A profundidade de imersão da concha para reduzir a velocidade a 100 m/s após percorrer a distância L.
Solução: Aplique a componente x da equação de quantidade de movimento usando o VC com aceleração linear mostrado.
Equação básica:
ϭ
ϩ Ϫ ϭ ϩ и
0 1 0 2( ) ( )Ϸ
F F a d
t
u d u V dAS B
VC
rfx xyz xyz xyz
SCVC
x x ∫ ∫∫∀
∂
∂
∀
r r
Considerações: (1) FBx ϭ 0.
(2) Despreze taxa de variação de u dentro do VC.
(3) Escoamento uniforme em cada seção.
(4) Nenhuma variação na velocidade relativa do líquido na concha.
Então,
Ϫ Ϫ ϭ Ϫ ϩ ϭ
ϭ Ϫ ϭ
ϭ ϭ ϫ ϫ ϫ
и
и
ϭ
Ϫ Ϫ ϭ ϩ ϭ
Ϫ
F Ma u Uwh u Uwh h imersão da concha
u U u U
Mas F kU k
F
U
kN
s
m
N
kN
kg m
N s
kg m
kU M
dU
dt
U wh posto que a dU dt
Assim
D rfx
D
D
rtx
1 2
1 2
2 0
0
2
2 2
3
2
2 2
2
90
300
10
1 00
1
{ } { };
cos
;
( )
, /
( cos ), / .
, MM
dU
dt
k wh U MU
dU
dX
ou
dU
U
CdX onde C
k wh
M
Integrando
U
U
CX o C
X
U
U
C
m
m
ϭ ϩ ϩ ϭ Ϫ
ϭ Ϫ ϭ
ϩ ϩ
ϭ Ϫ ϭ Ϫ
ϭ Ϫ ϭ ϫ Ϫ Ϫ
( cos
,
( cos )
, ln , log ln
ln ,
1
1
1
1
800
100
300
1 37 10
2
0 0
3 1
)[ ]
CAP004/4 11/6/02, 9:30 AM52](https://image.slidesharecdn.com/capitulo4-160329182248/85/Solucionario-Capitulo4-FOX-52-320.jpg)
![Resolvendo para h h
MC k
w
h kg
m
kg
m
m
kg m
m
h mm h
,
( cos )
,
,
, cos
,
,
ϭ
Ϫ
ϩ
ϭ ϫ
ϫ
Ϫ ϫ ϫ
ϩ
ϭ
ϭ
Ϫ
1
8000
1 37 10
1 00
999
1
0 3
1
1 30
0 0179
17 9
3 3
°( )
←
Problema 4.143
Dados: Foguete trenó com massa inicial de 4000 kg, incluindo 1000 kg de combustível. A resistência ao movimento é dada
por kU com k ϭ 75 N/m/s.
Determine: A velocidade do trenó 10 s após a partida do repouso.
Plote: A velocidade e a aceleração do trenó como funções do tempo.
Solução: Aplique a componente x da equação da quantidade de movimento ao VC com aceleração linear mostrado.
Equação básica:
ϭ
ϩ Ϫ ϭ ϩ и
0 2 0 3( ) ( )
( )F F a d
t
u d u V dAS B rfx
VC
xyz
VC
xyz xyz
SC
x x
∀
∂
∂
∀∫ ∫ ∫
r r
Considerações: (1) pe ϭ patm (dado), logo F FS Rx
ϭϪ .
(2) FBx
ϭ 0.
(3) Despreze efeitos transientes dentro do VC.
(4) Escoamento uniforme no plano de saída.
Então,
Ϫ Ϫ ϭ ϩ ϭϪ ϭ ϭϪF a M u m V m F kU VR rfx e e R e
˙ ˙ ,{ } { }ue
Da continuidade, M M mtϭ Ϫ0
˙ . Substituindo com a
dU
dt
rfx ϭ
Ϫ Ϫ Ϫ ϭϪ
ϭ
Ϫ
Ϫ Ϫ
ϭ
Ϫ
Ϫ ϭ Ϫ
kU M mt
dU
dt
V m
dU
dt
V m kU
M mt
ou
dU
V m kU
dt
M mt
Integrando
k
V m kU
m
M mt
e
e
e
e
U t
( ˙ ) ˙
˙
˙ ˙ ˙
, ln ( ˙ ) ln ( ˙ )
0
0 0
0 0 0
1 1
] ]
CAP004/4 11/6/02, 9:30 AM53](https://image.slidesharecdn.com/capitulo4-160329182248/85/Solucionario-Capitulo4-FOX-53-320.jpg)


![Equações básicas:
0
0 1 0 2 0 3
ϭ ϩ и
ϭ ϭ
ϩ Ϫ ϭ ϩ и
∂
∂
∀
( )
∀
∂
∂
∀
∫ ∫
∫ ∫ ∫
t
d V dA
F F a d
t
u d u V dA
VC
xyz
SC
S B rfx
VC
xyz
VC
xyz
SC
xyzx x
r r
r r
( ) ( ) )Ϸ
Considerações: (1) FSx
ϭ 0.
(2) FBx
ϭ 0.
(3) Despreze u dentro do VC.
(4) Escoamento uniforme no jato.
Da continuidade,
0 ϭ ϩ Ϫ Ϫ ϭ Ϫ
∂
∂
{ }t
M V U A ou
dM
dt
V U Avc ( ) ( )
Da quantidade de movimento,
Ϫ ϭϪ ϭ Ϫ Ϫ ϭ Ϫ Ϫ Ϫ ϭ Ϫ
Ϫ ϭ ϭϪ Ϫ
Ϫ ϭ
Ϫ
ϭϪ Ϫ Ϫ ϭ ϭ
ϭ
a M
dU
dt
M u V U A V U V U A u V U
Mas da continuidade V U A
dM
dt
e dU d V U por to
dU
dt
M
d V U
dt
M V U
dM
dt
ou M V U cons te M V
Assim M M
rfx
o
o
( ) ( ) ( ) ;
, ( ) , ( ), tan ,
( )
( ) ( ) tan
,
{ } [ ]
VV V U M/( )Ϫ ←
Substituindo na quantidade de movimento,
Ϫ ϭ
Ϫ
Ϫ
ϭϪ Ϫ
dU
dt
M
d V U
dt
M V
V U
V U Ao( )
( )
( ) 2
ou
d V U
V U
A
VM
dt
o
( )
( )
Ϫ
Ϫ
ϭ Ϫ3
Integrando,
d V U
V U V U V
A
VM
dt
A
VM
t
V
V U
oo
t
o
( )
( ) ( )
Ϫ
Ϫ
ϭϪ
Ϫ
Ϫ ϭϪ ϭϪ
Ϫ
3 2 2
1
2
1 1
∫ ∫
Resolvendo,
U
V VA
M
t
U
V
ϭ Ϫ
ϩ
1
1
1
2
0
1 2
←
/
CAP004/4 11/6/02, 9:30 AM56](https://image.slidesharecdn.com/capitulo4-160329182248/85/Solucionario-Capitulo4-FOX-56-320.jpg)


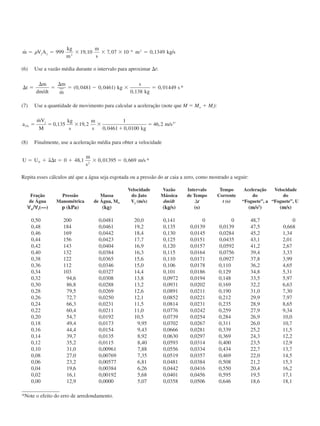




![Equação básica:
ϭ ϭ ϭ
ϫ ϩ ϫ ϩ
ϭ ϭ
Ϫ ϫ ϫ ϩ ϫ ϫ ϩ ϫ
ϭ
ϭ ϫ ϩ ϫ и
0 1 0 2 0 3
0 5 0 6
2
0 6
( ) ( ) ( )
( ) ( )
( )
( )
r r r
r r r r r r r
r r r r r r
r F r g d T
r V r r d
t
r V d r V V dA
S
VC
eixo
xyz
VC
xyz
VC
xyz
SC
xyz
∫
∫
∫ ∫
∀
[ ] ∀
∂
∂
∀
Considerações: (1)
r
FS ϭ 0. (2)Torques de campo anulam-se. (3)
r
Teixo ϭ 0. (4)Arrasto aerodinâmico desprezível. (5) Nenhuma
componente ˆk da aceleração centrípeta. (6) Escoamento permanente. (7) L Ӷ R.
Analise um braço do regador. Da geometria,
r r
r ri r Riϭ ϭˆ , ˆno VC no jato. Então,
Ϫ ϫ ϫ ϭ ϫ Ϫ ϭϪ
ϫ ϫ ϭ Ϫ ϭϪ
Ϫ ϭϪ ϭ
ϭ ϭ
r r r
r V d Ri Vsen j
Q QRV
sen k
ri k Vi Vr k VR A k
E inando k VR A
QRV
sen por to com VA Q
V
R
sen V
Q
xyz
VC
VC
2
3 3
2 2
3
3
3
2
2
[ ] ∀∫
∫
ˆ ( ˆ) ˆ
ˆ ( ˆ ˆ) ˆ; ˆ
lim ˆ, , tan , / ,
;
AA
Q
d
m
m s
m s
m
s m
sen sen rad s
ϭ ϭ ϫ ϫ ϫ ϫ ϭ
ϭ ϫ ϫ ϭ
Ϫ
4
3
4
3
68 10
1
0 00635 60
11 9
11 9
1
0 152
78 3
2
3
3
2 2
min ( , )
min
, /
,
,
, / ←
Traçando os gráficos:
(graus)
Para
Gráfico
CAP004/5 11/4/02, 2:37 PM68](https://image.slidesharecdn.com/capitulo4-160329182248/85/Solucionario-Capitulo4-FOX-68-320.jpg)
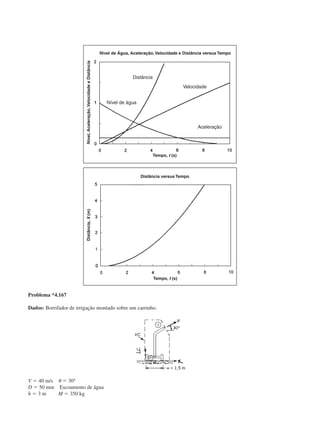
![Problema *4.174
Dados: Tubo rotativo simples com água. Q ϭ 13,8 L/min.
Determine: O torque que deve ser aplicado para manter rotação em regime permanente usando:
(a) Volume de controle rotativo.
(b) Volume de controle fixo.
Solução: Aplique o princípio da quantidade de movimento angular, ϭ ϭ33
1
3
3 49
rev
rad s
min
, /
(a) VC rotativo: use velocidades relativas, Eq. 4.53.
Equação básica:
ϭ ϭ
ϫ ϩ ϫ ϩ
ϭ ϭ
Ϫ ϫ ϫ ϩ ϫ ϫ ϩ ϫ
ϭ ϭ
ϭ ϫ ϩ ϫ и
0 1 0 2
0 3 0 4
2
0 5 0 6
( ) ( )
( ) ( )
( )
( ) ( )
r r r r
r r r r r r r r
r r r r r r
r F r g d T
r V r r d
t
r V d r V V d
S
VC
eixo
xyz
VC
xyz
VC
xyz
SC
xyz
∀
[ ] ∀
∂
∂
∀
∫
∫
∫ ∫ AA
Considerações: (1)
r
FS ϭ 0. (2) Torques de campo anulam-se. (3) Nenhuma componente ˆk da aceleração centrípeta. (4)
r˙ . ϭ 0 (5) Escoamento permanente. (6)
r r
r Vϫ ϭ 0.
Então,
T k r V d rı k Vı Adr VAR k Q R k
T
rad
s
kg
m
m
m
s
N s
kg m
N m
T
eixo
o
R
VC
eixo
ˆ ( ) ˆ ( ˆ ˆ) ˆ ˆ
, ,
min
( , )
min
,
ϭ ϫ ϫ ϭ ϫ ϫ ϭ ϭ
ϭ ϫ ϫ ϫ ϫ ϫ ϫ
и
и
ϭ иϪ
r r r
2 2
3 49 999 13 8 10 0 3
60
0 0722
2 2
3
3
3
2 2
2
∀
←
∫∫
(b) VC fixo: use velocidades absolutas, Eq. 4.47.
CAP004/5 11/4/02, 2:37 PM69](https://image.slidesharecdn.com/capitulo4-160329182248/85/Solucionario-Capitulo4-FOX-69-320.jpg)

![Considerações: (1) Despreze torque devido a forças de superfície.
(2) Torques de forças de campo cancelam-se por simetria.
(3) Escoamento permanente.
(4) Escoamento uniforme em cada jato.
Então,
Ϫ ϭ ϫ Ϫ ϩ ϫ
ϫ ϭ
ϭ Ϫ ϩ
T k r V Q r V Q
r V r Ri
V R V i V sen i
eixo entrada jato
entrada r
rel re z
ˆ ( ) ( )
( ) ˆ
( cos )ˆ ˆ
r r r r
r r r
r
␣ ␣
{ }
2
1
2
0
1
Ӎ
O jato sai do regador a
r
V abs V i sen irel z( ) cos ( ˆ ) (ˆ )ϭ Ϫ ϩ␣ ␣[ ]
Portanto,
r r
r V Ri V i sen i RV i sen ir rel z rel zϫ ϭ ϫ Ϫ ϩ ϭ Ϫ ϩ Ϫˆ cos ( ˆ ) (ˆ ) cos ( ˆ ) ( ˆ )␣ ␣ ␣ ␣ [ ] [ ]
Somando os momentos sobre o rotor, Α
r r
M Iϭ . Dessa forma,
˙
cos
min
, ,
min
,
,
˙ , / ˙
ϭ ϭ
Ϫ
ϭ ϫ ϫ ϫ ϫ ϫ ϫ Ϫ и ϫ
и
и и
ϭ
ΑT
I
QRV T
I
kg
m
L
m
m
s
m
L s
N m
kg m
N s kg m
rad s
rel eixo ␣
999 4 0 2 17 0 866
1000 60
0 18
1
0 1
0 161
3
3
2 2
2
←
{Não é necessário usar um VC rotativo porque, para o instante considerado,
r
ϭ 0 e I é conhecido.}
Problema *4.178
Dados: Conjunto de bocal girando em regime permanente, conforme mostrado no esquema
Coordenadas
xyz giram
com VC
VC rotativo
Coordenadas XYZ
são fixas
CAP004/5 11/4/02, 2:37 PM71](https://image.slidesharecdn.com/capitulo4-160329182248/85/Solucionario-Capitulo4-FOX-71-320.jpg)
![Determine: (a) Torque requerido para mover o conjunto.
(b) Torques de reação no flange.
Solução: Aplique a equação do momento da quantidade de movimento ao VC rotativo mostrado.
Equação básica:
Ϸ 0 2
0 3 0 5 0 7
2
( )
( ) ( ) ( )
( ) ˙
r r r r r
r r r r r r r r r r r r r r
r F r g d T
r V r r d
t
r V d r V V dA
S
VC
eixo
VC
xyz xyz
VC
xyz
VC
xyz
ϫ ϩ ϫ ϩ
ϭ ϭ ϭ
Ϫ ϫ ϫ ϩ ϫ ϫ ϩ ϫ ϭ ϫ ϩ ϫ и
∫
∫ ∫ ∫
∀
[ ] ∀
∂
∂
∀
Considerações: (1)
r
TVC representa todos os torques atuando sobre o VC.
(2) Despreze torque devido à força de campo.
(3) Velocidade angular constante.
(4) Despreze a massa do braço comparada com a massa de água no seu interior.
(5) Escoamento permanente no VC.
(6) Despreze comprimento do bocal comparado com L.
(7)
r
r colinear com
r
V, logo,
r r
r Vxyzϫ ϭ 0.
Então,
r r r r r r r
r r
r r
r r r
r r r r
T r V r d
Posto que k e r l sen ı k então
r l sen j
r k l sen j l sen ı
e r r
VC xyz
VC
ϭ ϫ ϫ ϩ ϫ ϫ
ϭ ϭ ϩ
ϫ ϭ
ϫ ϫ ϭ ϫ ϭ Ϫ
ϫ ϫ ϫ
2
2
( )
ˆ ( ˆ cos ˆ),
ˆ
( ) ˆ ˆ ( ˆ)
( )
[ ] ∀
[
∫
]]
[ ]
ϭ ϩ ϫ Ϫ ϭ Ϫ
ϭ ϩ
ϫ ϭ ϫ ϩ ϭ
ϫ ϫ ϭ
l sen ı k l sen ı l sen j
Posto que V V sen ı k então
V k V sen ı k V sen j
e r V l sen ı
xyz VC
xyz VC VC
xyz
( ˆ cos ˆ) ( ˆ) cos ( ˆ)
( ˆ cos ˆ),
ˆ ( ˆ cos ˆ) ˆ
( ˆ
2 2 2
2 2 2
2
r
r r
r r r
ϩϩ ϫ ϭ
ϩ Ϫ
cos ˆ) ˆ ˆ
cos ( ˆ)
k V sen j l V sen k
l V sen ı
VC VC
VC
2 2
2
2
Substituindo e introduzindo d dl∀ ∀ϭ ,
r
r
T lV sen i l sen j lV sen k Adl
T L V sen i
L
sen j L V sen k A
VC VC VC
L
VC VC VC
ϭ Ϫ Ϫ ϩ
ϭ Ϫ Ϫ
ϩ
( cos ˆ cos ˆ ˆ)
cos ˆ cos ˆ ˆ
2 2
3
2 2 2
0
2
2 3
2 2
∫
CAP004/5 11/4/02, 2:37 PM72](https://image.slidesharecdn.com/capitulo4-160329182248/85/Solucionario-Capitulo4-FOX-72-320.jpg)

![Determine: A potência requerida.
Solução: Aplique a primeira lei da termodinâmica, usando o VC mostrado.
Equação básica:
ϭ ϭ
Ϫ Ϫ ϭ ϩ ϩ и
0 1 0 2( ) ( )
˙ ˙ ˙ ( )Q W W
t
e d e pv V dAs cisalhamento
SCVC
∂
∂
∀ ∫∫
r r
Considerações: (1) ˙ .Wcisalhamento ϭ 0
(2) Escoamento permanente.
(3) Escoamento uniforme em cada seção.
(4) Despreze ⌬z.
(5) Gás ideal, p RT h Cp T Cp kJ kg kϭ ⌬ ϭ ⌬ ϭ и , ; , / .1 00
(6) Da continuidade, ˙ ˙ ˙.m m m1 2ϭ ϭ
Então,
Ϸ Ϸ0 4 0 4
2 2
2
2
2
2
2 1 2 1
1
2
1 1 1
2
2
1
2
2 1
( ) ( )
˙ ˙ ( ) ˙ ( ) ˙
, ˙ ˙ , tan ,
˙ ˙ ˙
Q W u
V
gz p v m u
V
gz p v m
Note que h u pv e Q m
dQ
dm
por to
W W m
V V
h h
dQ
dm
s
entrada s
Ϫ ϭ ϩ ϩ ϩ ϩ ϩ ϩ ϩ Ϫ
ϭ ϩ ϭ
ϭϪ ϭ
Ϫ
ϩ Ϫ Ϫ
{ } { }
ϭϭ
Ϫ
ϩ Ϫ Ϫ
ϭ Ϫ ϫ
и
и
ϫ
и
ϩ
и
Ϫ Ϫ Ϫ
и
ϭ
˙ ( )
˙ , ( ) ( )
, ( )
˙ ,
˙
m
V V
cp T T
dQ
dm
ou
W
kg
s
m
s
N s
kg m
kJ
N m
kJ
kg k
K
kJ
kg
kW s
kJ
W kW
entrada
entrada
2
2
1
2
2 1
2 2
2
2
2
2
1 0
1
2
125 75
1000
1 00 345 288 18
80 0
[ ]
WWentrada
←
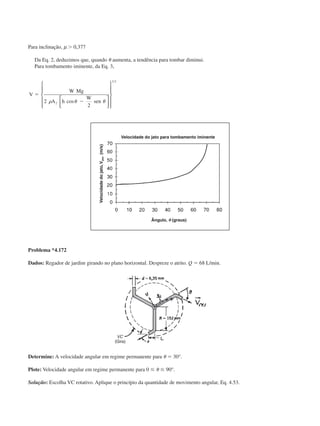
Problema 4.184
Dados: Escoamento através de turbomáquina conforme mostrado. O fluido é ar.
(da atmosfera)
(manométrica)
CAP004/5 11/4/02, 2:37 PM74](https://image.slidesharecdn.com/capitulo4-160329182248/85/Solucionario-Capitulo4-FOX-74-320.jpg)




![Equações básicas:
ϭ ϭ
ϭ ϭ ϭ ϭ ϭ ϭ
Ϫ Ϫ Ϫ ϭ ϩ ϩ ϩ ϩ и
˙
˙
( ) ( ) ( ) ( ) ( ) ( )
˙ ˙ ˙ ˙
W
onde W potência para o fluido
Q W W W
t
k d u pv
V
gz V dA
s
entrada
s
s cisalhamento outros
SCVC
ᏼ
0 1 0 2 0 2 0 3 0 4 0 5
2
2
∂
∂
∀
∫∫
r r
Considerações: (1) ˙Q ϭ 0 (isolado).
(2) ˙Wcisalhamento ϭ 0 (pela escolha do VC); ˙ .Woutros ϭ 0
(3) Escoamento permanente.
(4) Despreze ⌬u.
(5) ⌬z ϭ 0.
(6) Escoamento incompressível.
(7) Escoamento uniforme na entrada e na saída.
Então,
Ϫ ϭ ϩ Ϫ ϩ ϩ Ϫ
ϭ ϭ
Ϫ ϭ Ϫ ϭ Ϫ
ϭ ϭ
ϭ ϫ ϫ
˙ ˙ ˙
˙ ( )
˙ ( ) ( )
, ,
W p
V
m p
V
m
Visto que m Q e V V da continuidade
W Q p p Q p p
p gh SG gh
p
slug
ft
s i
s
H O
1
1
2
2 2
2
2
1 2
2 2 1 1 2 1
1
1 3
2 2
13 6 1 94
2
v v
v v
{ }
{ }
3232 2 8
12 144
3 93
300
7 48 60
35 3 93
144
550
2
2 2
2
3
2
2
2
, ( ) ,
˙
min ,
min
( , )
ft
s
in
ft
in
lbf s
ft slug
ft
in
psig
W
gal ft
gal s
lbf
in
in
ft
hp s
ft lbf
s
ϫ Ϫ ϫ ϫ
ϫ
и
ϫ ϭϪ
Ϫ ϭ ϫ ϫ ϫ Ϫ Ϫ ϫ ϫ
и
и
∴ [ ]
˙ ,Ws ϭϪ6 81 hp (o sinal negativo indica energia adicionada)
Portanto,
ϭ ϭ ϭ
˙ ,
,
, ,
W
ou por centos
entradaᏼ
6 81
9 1
0 748 74 8 ←
Problema 4.189
Dados: Barco de combate a incêndio.
superfície da água
CAP004/5 11/4/02, 2:37 PM79](https://image.slidesharecdn.com/capitulo4-160329182248/85/Solucionario-Capitulo4-FOX-79-320.jpg)


![Determine: (a) Velocidade do ar saindo do aparelho.
(b) Potência mínima requerida.
Solução: Use oVC inercial e as coordenadas mostradas.Aplique a continuidade e a quantidade de movimento para determinar
V2, em seguida, aplique a primeira lei para determinar a potência.
Equações básicas:
p RT h c T
p V
gz cons te
t
d V dA
F F
t
d V dA
p
VC SC
S B
VC SC
z z
ϭ ⌬ ϭ ⌬ ϩ ϩ ϭ
ϭ
ϭ ϩ и
ϭ
ϩ ϭ ϩ и
; ; tan
( )
( )
2
2
0 2
0
0 2
∂
∂
∀
∂
∂
∀
∫ ∫
∫ ∫
r r
r r
Considerações: (1) O ar é um gás ideal, cp ϭ constante.
(2) Escoamento permanente.
(3) Escoamento incompressível.
(4) Escoamento uniforme em cada seção.
(5) Pressão uniforme na entrada; F p p A p AS atm gz
ϭ Ϫ ϭϪ( ) .1 1 1 1
Então,
ϭ ϭ ϫ ϫ
и
и
ϫ ϭ
p
RT
N
m
kg k
N m k
kg m1 01 10
287
1
288
1 225
2
3
, , /
e da continuidade
0
4 4
3 3 8 55
4 4
3 3 3 0 1 48
1 1 2 2 2 2 1 1 1 2
2
1
1 0
2 2 2 2
2 0
2
2
2 2 2 2 2
ϭ Ϫ ϩ ϭ Ϫ ϭ
ϭ ϭ ϭ
ϭ Ϫ ϭ Ϫ ϭ
V A V A V A V A ou V V
A
A
Então A D m m
A D D m m
{ } { }
( ) ( )[ ]
( )
( , ) ,
( ) , , ,
Da quantidade de movimento
Ϫ Ϫ ϭ Ϫ ϩ
ϭϪ ϭϪ ϭ
Ϫ Ϫ ϭ Ϫ ϭϪ Ϫ
p A Mg V A V A
V V e V A V A
p A Mg V V A V V A V A V V
g
g
1 1 1 1 1 2 2 2
1 1 2 2 1 1 2 2
1 1 1 2 2 2 2 2 2 2 2 1
{ } { }
( )
Para escoamento permanente, incompressível, sem atrito, ao longo de uma linha de corrente da atmosfera para ቢ, Bernoulli
fornece, desprezando ⌬z,
Ϸ 0
1
2
1
2
1
2
0
2
1 1
2
1 1 1
2
p V gz p V gz por to p Vatm o gϩ ϩ ϭ ϩ ϩ ϭϪ , tan
CAP004/5 11/4/02, 2:38 PM82](https://image.slidesharecdn.com/capitulo4-160329182248/85/Solucionario-Capitulo4-FOX-82-320.jpg)
