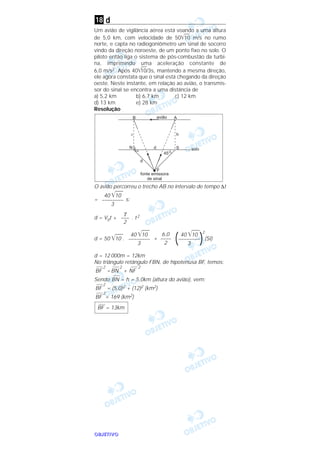
1) O documento descreve os regimes laminar e turbulento de escoamento de fluidos.
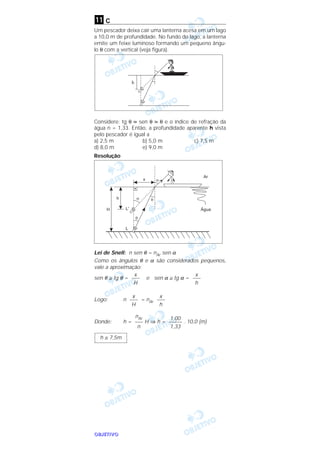
2) O número de Reynolds (R) é um parâmetro que depende da velocidade, densidade, viscosidade do fluido e dimensão característica do meio, e determina o regime de escoamento.
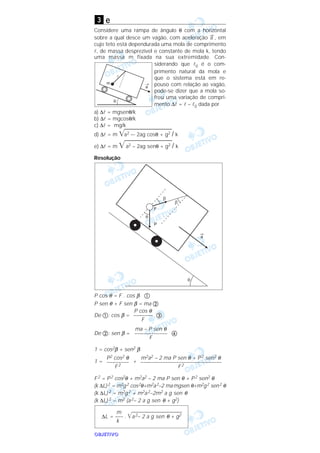
3) A força de arrasto em uma esfera em movimento em um fluido é dada por uma expressão que depende do diâmetro da esfera e da velocidade e viscosidade do fluido.
![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
a
Quando camadas adjacentes de um fluido viscoso des-
lizam regularmente umas sobre as outras, o escoa-
mento resultante é dito laminar. Sob certas condições,
o aumento da velocidade provoca o regime de escoa-
mento turbulento, que é caracterizado pelos movi-
mentos irregulares (aleatórios) das partículas do fluido.
Observa-se, experimentalmente, que o regime de
escoamento (laminar ou turbulento) depende de um
parâmetro adimensional (Número de Reynolds) dado
por R = ραvβdγητ, em que ρ é a densidade do fluido, v,
sua velocidade, η, seu coeficiente de viscosidade, e d,
uma distância característica associada à geometria do
meio que circunda o fluido. Por outro lado, num outro
tipo de experimento, sabe-se que uma esfera, de diâ-
metro D, que se movimenta num meio fluido, sofre a
ação de uma força de arrasto viscoso dada por F
= 3πDηv. Assim sendo, com relação aos respectivos
valores de α, β, γ e τ, uma das soluções é
a) α = 1, β = 1, γ = 1, τ = – 1
b) α = 1, β = – 1, γ = 1, τ = 1
c) α = 1, β = 1, γ = – 1, τ = 1
d) α = – 1, β = 1, γ = 1, τ =1
e) α = 1, β = 1, γ = 0, τ = 1
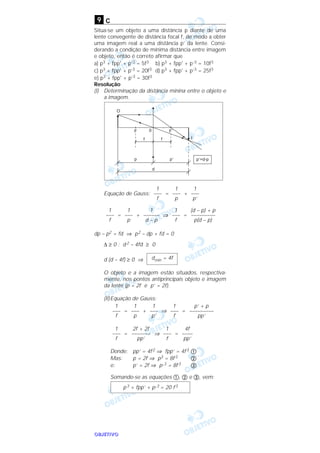
Resolução
1) F = 3π D η V
MLT–2 = L [η] L T–1
2) R = ρα Vβ dγ ητ
M0 L0 T0 = (M L–3)α (L T–1)β L
γ
(M L–1 T–1)
τ
M0 L0 T0 = Mα + τ L–3α + β + γ – τ T–β – τ
α + τ = 0
–3α + β + γ – τ = 0
–β – τ = 0
Como temos três equações e quatro incógnitas,
temos de optar por um valor de α sugerido nas
alternativas e procurarmos os demais valores:
1) 2)
3) 4) –3 + 1 + γ + 1 = 0
γ = 1
β = 1
τ = –1α = 1
[η] = M L–1 T–1
1](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/75/Ita2005-1-2048.jpg)














![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
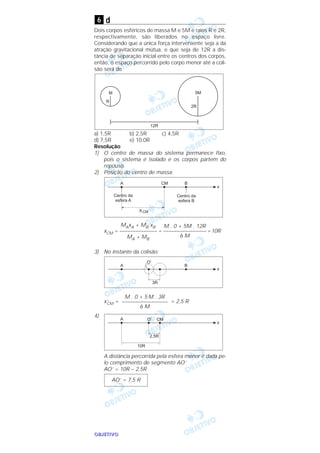
Inicialmente 48g de gelo a 0°C são colocados num calo-
rímetro de alumínio de 2,0g , também a 0°C. Em segui-
da, 75g de água a 80°C são despejados dentro desse
recipiente. Calcule a temperatura final do conjunto.
Dados: calor latente do gelo Lg = 80cal/g, calor especí-
fico da água cH2O = 1,0 cal g–1 °C–1, calor específico do
alumínio cAl = 0,22 cal g–1°C–1.
Resolução
Fazendo o balanço energético, temos:
Qcedido + Qrecebido = 0
(mc∆θ)água + [(mLg)gelo + mc∆θ] + (mc∆θ)calorímetro = 0
75 . 1,0 . (θf – 80) + 48 . 80 + 48 . 1,0 . (θf – 0) +
+ 2,0 . 0,22 . (θf – 0) = 0
75 θf – 6000 + 3840 + 48 θf + 0,44 θf = 0
123,44 θf = 2160
Resposta: 17,50°C
θf = 17,50°C
22](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-21-320.jpg)
























![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
TEXTO 2
A Universidade é só o começo
Na última década, a universidade viveu uma
espécie de milagre da multiplicação dos diplomas.
O número de graduados cresceu de 225 mil no final
dos anos 80 para 325 mil no levantamento mais
recente do Ministério da Educação em 2000.
A entrada no mercado de trabalho desse con-
tingente, porém, não vem sendo propriamente
triunfal como uma festa de formatura. Engenheiros
e educadores, professores e administradores, es-
critores e sobretudo empresários têm sussurrado
uma frase nos ouvidos dessas centenas de milha-
res de novos graduados: "O diploma está nu".
Passaporte tranqüilo para o emprego na dé-
cada de 80, o certificado superior vem sendo exi-
gido com cada vez mais vistos.
Considerado um dos principais pensadores da
educação no país, o economista Cláudio de Moura
Castro sintetiza a relação atual do diploma com o
mercado de trabalho em uma frase: "Ele é neces-
sário, mas não suficiente". O raciocínio é simples.
Com o aumento do número de graduados no mer-
cado, quem não tem um certificado já começa em
desvantagem.
Conselheiro-chefe de educação do Banco
Interamericano de Desenvolvimento durante anos,
ele compara o sem-diploma a alguém "em um mato
sem cachorro no qual os outros usam armas auto-
máticas e você um tacape". Por outro lado, o eco-
nomista-educador diz que ter um fuzil, seja lá qual
for, não garante tanta vantagem assim nessa flo-
resta.
Para Robert Wong, o diagnóstico é semelhan-
te. Só muda a metáfora. Principal executivo na
América do Sul da Korn/Ferry International, maior
empresa de recrutamento de altos executivos do
mundo, ele equipará a formação acadêmica com a
potência do motor de um carro.
Equilibrados demais acessórios, igualado o preço,
o motor pode desempatar a escolha do consumidor.
"Tudo sendo igual, a escolaridade faz a diferença."
Mas assim como Moura Castro, o head hunter
defende a idéia de que um motor turbinado não
abre automaticamente as portas do mercado.
Wong conta que no mesmo dia da entrevista à
Folha [Jornal Folha de S. Paulo] trabalhava na se-
leção de um executivo para uma multinacional na
qual um dos principais candidatos não tinha expe-
riência acadêmica. "É um self-made man."
Brasileiro nascido na China, Wong observa que
é em países como esses, chamados "em desen-
volvimento", que existem mais condições hoje para
o sucesso de profissionais como esses, de perfil
empreendedor. (...)
(Cassiano Elek Machado: A universidade é só o
começo. Folha de S. Paulo, 27/07/2002.
Disponível na Internet:
http://www1.folha.uol.com.br/folha/sinapse. Data de aces-
so: 24/08/2004)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
IIIITTTTAAAA ---- ((((2222ºººº ddddiiiiaaaa)))) DDDDeeeezzzzeeeemmmmbbbbrrrroooo////2222000000004444](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-49-320.jpg)





![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
As questões 30 e 43 (questão dissertativa) referem-
se ao texto a seguir
Ao Teatro o que é do teatro
INÁCIO ARAÚJO
..............................
Crítico da FOLHA
Não há melhor maneira de filmar o teatro do que
teatralmente. A expressão “teatro filmado” raramente
faz sentido, e nós aqui no Brasil só teríamos a ganhar
no dia em que pudéssemos assistir ao filme de “O Rei
da Vela” do Oficina – que por alguma razão infeliz nunca
passa.
Kenneth Branagh evitou o teatro filmado em “Hen-
rique V” (Eurochannel, 0h) [canal de TV por assinatura],
ganhou o direito a concorrer ao Oscar e ficou famoso.
Mas, passadas as festas, temos um resultado para lá
de duvidoso.
Onde faz sentido a conclamação do rei Henrique a
seus soldados a não ser no teatro? E por que “cinema-
tografizar” a coisa se Joseph Mankiewicz, por exemplo,
que era um cineasta, ao filmar “Júlio César”, optou por
deixar clara a origem teatral de seu filme?
(Folha de S. Paulo, 11/5/04)
e
Considerando o texto acima, assinale a opção correta.
a) O título já evidencia a tese do autor: não se deve fil-
mar peça teatral.
b) As falas dos personagens em peças de teatro não
fazem sentido se filmadas.
c) Uma peça teatral pode ser filmada se, como faz
Mankiewicz, sua origem for indicada na apresen-
tação do filme.
d) “Henrique V” só concorreu ao Oscar porque igno-
rou a natureza teatral da obra original.
e) “O Rei da Vela”, na sua versão cinematográfica, é
um exemplo de teatro filmado.
Resolução
A melhor alternativa, no caso, é aquela que, sem colo-
car a questão central da relação teatro / cinema, apenas
menciona, a título de exemplo de “teatro filmado”, o
filme O Rei da Vela, derivado da peça teatral de Oswald
de Andrade, que o Teatro Oficina encenou, quer como
teatro, na década de 60, quer como cinema, nos anos
80. O texto pioneiro de Oswald, que inaugura a drama-
turgia modernista, na década de 30, só foi levado ao
palco no fim dos anos 60, com direção de José Celso
Martinez Correa, que também dirigiu a versão cinema-
tográfica, infelizmente não exibida ao público, como
lamenta o crítico.
30
IIIITTTTAAAA ---- ((((2222ºººº ddddiiiiaaaa)))) DDDDeeeezzzzeeeemmmmbbbbrrrroooo////2222000000004444](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-55-320.jpg)
![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
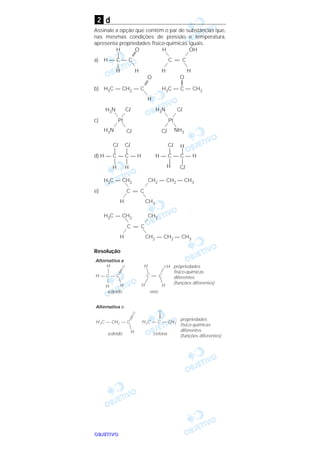
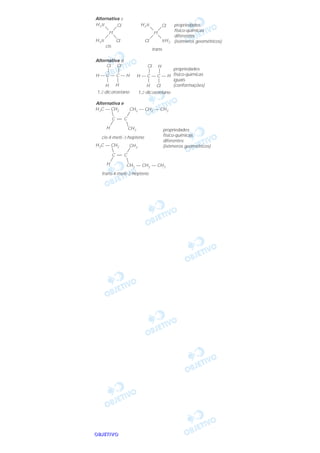
c
Das opções abaixo, cujos textos foram extraídos do
Manual do Proprietário de um carro, a única alternativa
que não apresenta inadequação quanto à construção
ou ao emprego de palavra é
a) Se o veículo costuma permanecer imobilizado por
mais que duas semanas ou se é utilizado em pe-
quenos percursos, com freqüência não diária (...)
adicione um frasco de aditivo.
b) Algumas [instruções], todavia, merecem atenção
especial, em virtude das graves conseqüências que
sua não observância pode representar para a inte-
gridade física dos ocupantes e para o funcionamen-
to do veículo.
c) Ao calibrar os pneus, não se esqueça de examinar
também o de reserva. Veja instruções na Seção 7,
sob Pneus.
d) Somente se a utilização do veículo ocorrer essen-
cialmente nas rodovias asfaltadas na maior parte do
tempo é que se pode proceder à troca de óleo a
cada 6 meses ou 10.000 km, o que primeiro ocor-
rer.
e) O uso dos cintos de segurança deve também ser
rigorosamente observado em veículos equipados
com sistema “Air bag”, que atua como com-
plemento a este sistema.
Resolução
A única dúvida que poderia assaltar os candidatos em
relação à alternativa c diz respeito ao emprego da pre-
posição sob. Tal emprego, não obstante, é correto e
preciso, pois não se trata de ver o que há, na seção 7,
sobre (“a respeito de”) pneus, mas sim de ler o con-
teúdo de uma das subdivisões da seção 7 – aquela en-
cabeçada pelo título Pneus (daí a maiúscula com que é
grafada essa palavra). Defeitos das demais alternativas:
a) imobilizado (“com os movimentos tolhidos”), por
“imóvel”, “parado”; b) representar, por “causar, acar-
retar”, ou mesmo “apresentar”; d) “na maior parte do
tempo” é adjunto adverbial de ocorrer e deveria vir ao
lado dessa palavra, não ao lado de asfaltadas, onde pro-
duz ambigüidade; e) a este, por “àquele”, se o sistema
de “air bags” complementar o sistema de cintos segu-
rança. No caso de o sistema de cintos funcionar como
complemento do de “air bags”, a oração adjetiva deve-
ria ser reformulada e reposicionada: O uso de cintos de
segurança, que funcionam como complemento do sis-
tema de “air bags”, deve ser rigorosamente observado.
31
IIIITTTTAAAA ---- ((((2222ºººº ddddiiiiaaaa)))) DDDDeeeezzzzeeeemmmmbbbbrrrroooo////2222000000004444](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-56-320.jpg)

![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
d
Considere o uso do particípio nas frases abaixo, extraí-
das do Texto 2:
I. Considerado um dos principais pensadores da edu-
cação no país, o economista Claúdio de Moura
Castro sintetiza a relação atual do diploma com o
mercado de trabalho em uma frase (…).
II. Equilibrados demais acessórios, igualado o preço, o
motor pode desempatar a escolha do consumidor.
III. Brasileiro nascido na China, Wong observa que é em
países como esses (…).
Considere ainda a seguinte regra gramatical:
“[…] a oração de particípio tem sujeito diferente do
sujeito da oração principal e estabelece, para com esta,
uma relação de anterioridade.”
(Cunha, C.; Cintra, L. Nova gramática do português
contemporâneo. Rio de Janeiro: Nova Fronteira,
1985:484)
Esta regra se aplica
a) apenas a I. b) a I e ll. c) a I e III.
d) apenas a II. e) a II e III.
Resolução
A frase II apresenta, para o particípio “equilibrados”, o
sujeito “acessórios”, e para o particípio “igualado”, o
sujeito “preço”, sendo ambos diferentes do sujeito da
oração principal, “o motor”, estabelecendo-se com
essa oração uma relação de anterioridade. Nas demais
frases, os sujeitos das orações participiais e os das prin-
cipais são os mesmos.
d
Inspirados no texto Reino Unido pode taxar fast food
contra obesidade (referente à questão 45), poderíamos
construir as manchetes abaixo. Aponte a opção em que
a manchete expressa uma relação causal entre os ele-
mentos envolvidos. Tenha em mente que nem todas as
cinco manchetes refletem a idéia central do texto.
a) Governo combate a obesidade
b) Governo financia instalações esportivas
c) Governo cobra taxas de empresas de fast food
d) Obesidade provoca morte
e) Obesidade cresce 400% em 25 anos
Resolução
A relação de causa e conseqüência fica evidente na
frase “Obesidade provoca morte”, sendo “obesidade”
a causa cujo efeito é “morte”.
35
34
IIIITTTTAAAA ---- ((((2222ºººº ddddiiiiaaaa)))) DDDDeeeezzzzeeeemmmmbbbbrrrroooo////2222000000004444](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-58-320.jpg)










![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO IIIITTTTAAAA ---- ((((3333ºººº ddddiiiiaaaa)))) DDDDeeeezzzzeeeemmmmbbbbrrrroooo////2222000000004444
Notações
ރ : conjunto dos números complexos.
ޑ : conjunto dos números racionais.
ޒ : conjunto dos números reais.
ޚ : conjunto dos números inteiros.
ގ = {0,1,2,3,...}.
=*ގ {1,2,3,...}.
Ø: conjunto vazio
AB ={x ∈ A; x ∉ B}.
[a,b] = {x ∈ ;ޒ a ≤ x ≤ b}.
]a, b[ = {x ∈ ;ޒ a < x < b}.
i : unidade imaginária; i2 = –1.
z = x + iy, x, y ∈ .ޒ
–
z : conjugado do número z ∈ .ރ
Izl: módulo do número z ∈ .ރ
—
AB : segmento de reta unindo os pontos A e B.
m(
—
AB): medida (comprimento) de
—
AB.
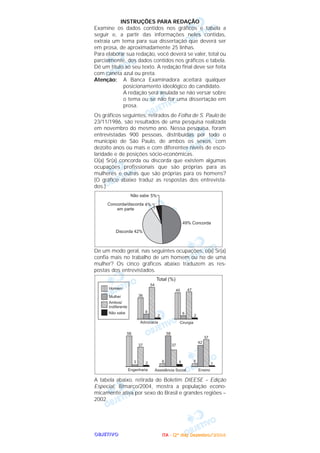
b
Considere os conjuntos S = {0, 2, 4, 6}, T = {1, 3, 5} e U
= {0,1} e as afirmações:
I. {0} ∈ S e S ʝ U ≠ Ø.
II. {2} ʚ SU e S ʝ T ʝ U = {0, 1}.
III. Existe uma função f: S → T injetiva.
IV. Nenhuma função g: T → S é sobrejetiva.
Então, é(são) verdadeira(s)
a) apenas I. b) apenas IV.
c) apenas I e IV. d) apenas II e III.
e) apenas III e IV.
Resolução
Se S = {0; 2; 4; 6}, T = {1; 3; 5} e U = {0; 1}, então
(I) é falsa, pois
0 ∈ S, mas {0} ∉ S e S ʝ U = {0} ≠ Ø
II) é falsa, pois
S U = S – U = {2; 4; 6} e {2} ʚ SU, mas
S ʝ T ʝ U = Ø
III) é falsa, pois
para f: S → T ser injetiva deveríamos ter
f(0) ≠ f(2) ≠ f(4), f(0) ≠ f(4) ≠ f(6) e
f(0) ≠ f(6) ≠ f(2) e, para isto, é necessário que
n(T) ≥ 4.
IV) é verdadeira, pois
para g:T → S ser sobrejetiva deveríamos ter
Im(g) = CD(g) = S, o que é impossível posto que
n[Im(g)] ≤ 3 e n(S) = 4.
1
MMMMAAAATTTTEEEEMMMMÁÁÁÁTTTTIIIICCCCAAAA](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-71-320.jpg)

![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
b
Sobre o número x = ͙ළළළළළළළළළ7 – 4͙ළළ3 + ͙ළළ3 é correto afirmar
que
a) x ∈ ]0, 2[. b) x é racional.
c) ͙ළළළ2x é irracional. d) x2 é irracional.
e) x ∈ ]2; 3[.
Resolução
x = ͙ළළළළළළළළළ7 – 4͙ළළ3 + ͙ළළ3 = ͙ළළළළළළළළළ(2 – ͙ළළ3)2 + ͙ළළ3 =
= 2 – ͙ළළ3 + ͙ළළ3 = 2
Portanto, x é racional.
d
Considere o triângulo de vértices A, B e C, sendo D um
ponto do lado
–––
AB e E um ponto do lado
–––
AC. Se
m(
–––
AB) = 8cm, m(
–––
AC) = 10cm, m(
–––
AD) = 4cm e
m(
–––
AE) = 6cm, a razão das áreas dos triângulos ADE e
ABC é
a) . b) . c) . d) . e) .
Resolução
Sendo α a medida dos ângulos congruentes B
^
AC e
D
^
AE, S1 a área, em centímetros quadrados, do triângulo
ADE e S2 a área, em centímetros quadrados, do triân-
gulo ABC, tem-se:
= = =
= =
3
–––
10
4 . 6
–––––
8 . 10
AD . AE
–––––––––
AB . AC
1
–– . AD . AE . sen α
2
–––––––––––––––––––
1
–– . AB . AC . sen α
2
S1
–––
S2
3
–––
4
3
–––
10
3
–––
8
3
–––
5
1
–––
2
5
4
IIIITTTTAAAA ---- ((((3333ºººº ddddiiiiaaaa)))) DDDDeeeezzzzeeeemmmmbbbbrrrroooo////2222000000004444](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-73-320.jpg)


![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
c
Uma esfera de raio r é seccionada por n planos meri-
dianos. Os volumes das respectivas cunhas esféricas
contidas em uma semi-esfera formam uma progressão
aritmética de razão . Se o volume da menor cunha
for igual a , então n é igual a
a) 4. b) 3. c) 6. d) 5. e) 7.
Resolução
Os n planos meridianos determinam nessa esfera um
total de 2n cunhas esféricas, das quais n estão contidas
em uma mesma semi-esfera, cujo volume é
Assim, a soma dos volumes dessas n cunhas é igual a
, ou seja:
= ⇔
⇔ + + n = ⇔
⇔ n2 + 4n – 60 = 0 ⇔ n = ⇔
⇔ n = 6, pois n > 0
e
Considere um prisma regular em que a soma dos ân-
gulos internos de todas as faces é 7200°. O número de
vértices deste prisma é igual a
a) 11. b) 32. c ) 10. d) 20. e) 22.
Resolução
Seja V o número total de vértices desse prisma regular.
A soma dos ângulos internos de todas as faces desse
poliedro convexo é dada por (V – 2) . 360°
Assim:
(V – 2) . 360° = 7200° ⇔ V – 2 = 20 ⇔ V = 22
9
– 4 + 16
––––––––
2
4
–––
3n – 1
–––––––
45
1
–––
18
1
–––
18
2πr3
––––
3
πr3 πr3 πr3
[–––– + ––– + (n – 1) –––– ]n
18 18 45
–––––––––––––––––––––––––––
2
2πr3
––––
3
2πr3
––––
3
πr3
–––
18
πr3
–––
45
8
IIIITTTTAAAA ---- ((((3333ºººº ddddiiiiaaaa)))) DDDDeeeezzzzeeeemmmmbbbbrrrroooo////2222000000004444](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-76-320.jpg)



![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
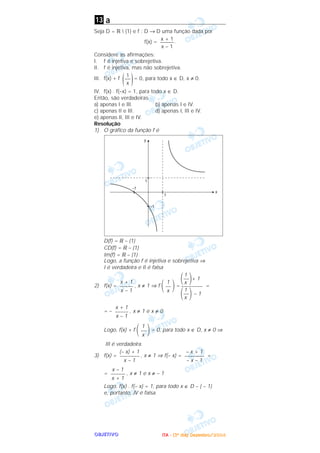
c
O intervalo I ʚ ޒ que contém todas as soluções da ine-
quação
arctan + arctan ≥ é
a) [–1, 4]. b) [–3, 1]. c) [–2, 3].
d) [0, 5]. e) [4, 6].
Resolução
1) arctg = α ⇒
⇒ tg α = com – < α <
2) arctg = β ⇒
⇒ tg β = com – < β <
Assim, temos:
= =
Se ≤ α + β < , então tan (α + β) ≥ tan ⇔
⇔ ≥ ⇔ x2 ≤ 4 ͙ළළ3 – 3 ⇔
⇔ – ͙ළළළළළළළළළ4͙ළළ3 – 3 ≤ x ≤ ͙ළළළළළළළළළ4͙ළළ3 – 3
Se < α + β < π, então tan(α + β) < 0 e a inequação
dada não apresenta solução, pois
tan(α + β) = > 0, ∀x ∈ .ޒ
Desta forma o intervalo I ʚ ޒ que contém todas as
soluções da inequação dada é I = [– 2; 3] pois:
– 2 ≤ – ͙ළළළළළළළළළ4͙ළළ3 – 3 ≤ x ≤ ͙ළළළළළළළළළ4͙ළළ3 – 3 ≤ 3
4
––––––
3 + x2
π
––
2
1
––––
͙ළළ3
4
–––––––
3 + x2
π
––
6
π
––
2
π
––
6
4
–––––––
3 + x2
1 + x 1 – x
–––––– + –––––
2 2
–––––––––––––––––––––
1 + x 1 – x
1 – –––––– . –––––2 2
π
α + β ≥ –––
6
– π < α + β < π
tan α + tan β
tan(α + β) = –––––––––––––––– =
1 – tan α . tan β
Ά
π
–––
2
π
–––
2
1 – x
–––––
2
1 – x
–––––
2
π
–––
2
π
–––
2
1 + x
–––––
2
1 + x
–––––
2
π
––
6
1 – x
–––––
2
1 + x
–––––
2
16
IIIITTTTAAAA ---- ((((3333ºººº ddddiiiiaaaa)))) DDDDeeeezzzzeeeemmmmbbbbrrrroooo////2222000000004444](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-81-320.jpg)
![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
d
Seja z ∈ ރ com |z| = 1. Então, a expressão
assume valor
a) maior que 1, para todo w com |w| > 1.
b) menor que 1, para todo w com |w| < 1.
c) maior que 1, para todo w com w ≠ z.
d) igual a 1, independente de w com w ≠ z.
e) crescente para |w| crescente, com |w| < |z|.
Resolução
Se z = x + yi, com x, y ∈ ޒ então
z .
–
z = (x + yi) . (x – yi) = x2 + y2 = |z|2 = 1
Assim, = =
= = | z–| = | z| = 1, para z ≠ w
a
O sistema linear
Ά
não admite solução se e somente se o número real b
for igual a
a) – 1. b) 0. c) 1. d) 2. e) – 2
Resolução
⇔
1) Sendo D o determinante dos coeficientes das incóg-
nitas, temos:
D = = b3 + 1 = 0 ⇔ b = –1, pois b ∈ .ޒ
2) Observemos que para b = –1 a matriz incompleta
MI = tem característica p = 2 e a ma-
triz completa MC =
tem característica q = 3.
3) Se p = 2 ≠ q = 3, pelo teorema de Rouché-Capelli, o
sistema é impossível.
]–1 1 0 1
0 –1 1 1
1 0 –1 1
[
]–1 1 0
0 –1 1
1 0 –1
[
|
b 1 0
0 b 1
1 0 b|
bx + y = 1
by + z = 1
x + bz = 1{
bx + y = 1
by + z = 1
x + bz = 1{
bx + y = 1
by + z = 1
x + bz = 1
18
|z– . (z – w)
––––––––––––
z – w|
|z . z– – z– . w
––––––––––––
z – w||1 – z– . w
––––––––––
z – w|
|1 – z
–
w
–––––––
z – w|
17
IIIITTTTAAAA ---- ((((3333ºººº ddddiiiiaaaa)))) DDDDeeeezzzzeeeemmmmbbbbrrrroooo////2222000000004444](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-82-320.jpg)




![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
Sejam A e B matrizes 2 x 2 tais que AB = BA e que
satisfazem à equação matricial A2 + 2AB – B = 0. Se B
é inversível, mostre que
(a) AB–1 = B–1A e que (b) A é inversível
Resolução
a) 1) Se B é inversível, então existe B–1, tal que
B . B–1 = I .
2) Sendo AB = BA, temos:
A = A ⇔ A . I = A ⇔ A . B . B–1 = A ⇔
⇔ B . A . B–1 = A ⇔ B–1. B . A . B–1 = B–1 . A ⇔
⇔ I . A . B–1 = B–1 . A ⇔ A . B–1 = B–1 . A
b) A2 + 2AB – B = 0 ⇔ B = A2 + 2AB ⇔
⇔ B = A . (A + 2B) ⇔
det B = det [A . (A + 2B)] = det A . det (A + 2B) ≠ 0,
pois B é inversível.
Se det A . det (A + 2B) ≠ 0, então det A ≠ 0 e, por-
tanto, A é inversível.
Seja n o número de lados de um polígono convexo. Se
a soma de n – 1 ângulos (internos) do polígono é 2004°,
determine o número n de lados do polígono.
Resolução
Seja α a medida, em graus, do n-ésimo ângulo interno
desse polígono convexo e seja Si a soma das medidas,
em graus, de todos os ângulos internos desse polígono.
Como 0° < α < 180°, pode-se então afirmar que:
2004° < Si < 2004° + 180° ⇔
⇔ 2004° < (n – 2) 180° < 2184° ⇔
⇔ 11 . 180° + 24° < (n – 2) 180° < 12 . 180° + 24° ⇔
⇔ 11 + < n – 2 < 12 + ⇔
⇔ n – 2 = 12, pois n ∈ .ގ
Assim: n = 12 + 2 ⇔ n = 14
Resposta: n = 14
2
–––
15
2
–––
15
24
23
IIIITTTTAAAA ---- ((((3333ºººº ddddiiiiaaaa)))) DDDDeeeezzzzeeeemmmmbbbbrrrroooo////2222000000004444](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-87-320.jpg)



![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
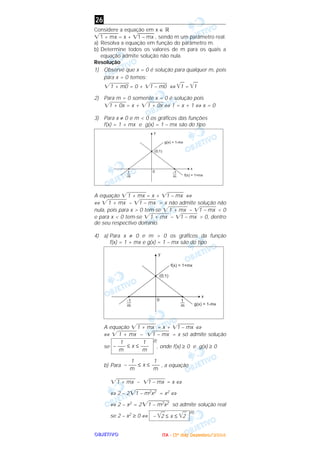
São dados dois cartões, sendo que um deles tem
ambos os lados na cor vermelha, enquanto o outro tem
um lado na cor vermelha e o outro na cor azul. Um dos
cartões é escolhido ao acaso e colocado sobre uma
mesa. Se a cor exposta é vermelha, calcule a probabili-
dade de o cartão escolhido ter a outra cor também ver-
melha.
Resolução
Nos dois cartões há quatro (4) faces: três (3) de cor ver-
melha e uma (1) de cor azul.
Se a cor exposta é uma das três (3) vermelhas então o
verso dessa face exposta será vermelha em dois (2)
casos e azul um (1) caso.
Logo, a probabilidade de o cartão escolhido (com a cor
exposta vermelha) ter a outra face também vermelha
é .
Resposta:
Obtenha todos os pares (x, y), com x, y ∈ [0, 2π], tais
que
sen (x + y) + sen (x – y) =
sen x + cos y = 1
Resolução
⇔
⇔
⇔ ⇔
e x, y ∈ [0,2π]
Teremos que:
x = π/6 ou x = 5π/6 e y = π/3 ou y = 5π/3
Resposta: (π/6; π/3); (π/6; 5π/3); (5π/6; π/3); (5π/6; 5π/3)
30
sen x = cos y = 1/2
sen x . cos y = 1/4
sen x + cos y = 1
2 sen x . cos y = 1/2
sen x + cos y = 1
1
sen (x + y) + sen (x – y) = –––
2
sen x + cos y = 1
1
—
2
29
2
–––
3
2
–––
3
V
A
V
V
IIIITTTTAAAA ---- ((((3333ºººº ddddiiiiaaaa)))) DDDDeeeezzzzeeeemmmmbbbbrrrroooo////2222000000004444](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-92-320.jpg)

![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
CONSTANTES
Constante de Avogadro = 6,02 x 1023 mol–1
Constante de Faraday (F) = 9,65 x 104C mol–1
Volume molar de gás ideal = 22,4 L (CNTP)
Carga elementar = 1,602 x 10–19 C
Constante dos gases (R) =
= 8,21 x 10–2 atm L K–1 moI–1 = 8,31 J K–1 moI–1 =
= 62,4 mmHg L K–1 mol–1 = 1,98 cal mol–1 K–1
DEFINIÇÕES
Condições normais de temperatura e pressão
(CNTP): 0°C e 760 mmHg.
Condições ambientes: 25°C e 1 atm.
Condições-padrão: 25°C, 1 atm, concentração das so-
luções: 1 mol L–1 (rigorosamente: atividade unitária das
espécies), sólido com estrutura cristalina mais estável
nas condições de pressão e temperatura em questão.
(s) ou (c) = sólido cristalino; (l) ou (l) = líquido; (g) = gás;
(aq) = aquoso; (graf) = grafite; (CM) = circuito metálico;
(conc) = concentrado; (ua) = unidades arbitrárias;
[A] = concentração da espécie química A em mol L1–.
MASSAS MOLARES
Massa Molar
(g mol–1
)
1,01
4,00
12,01
14,01
16,00
19,00
22,99
24,31
26,98
28,09
30,97
32,06
35,45
39,95
39,10
40,08
Número
Atômico
1
2
6
7
8
9
11
12
13
14
15
16
17
18
19
20
Elemento
Químico
H
He
C
N
O
F
Na
Mg
Al
Si
P
S
Cl
Ar
K
Ca
Química](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-95-320.jpg)

![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
c
Esta tabela apresenta a solubilidade de algumas subs-
tâncias em água, a 15°C:
Quando 50 mL de uma solução aquosa 0,10 moI L–1 em
sulfato de zinco são misturados a 50 mL de uma solu-
ção aquosa 0,010 moI L–1 em sulfito de sódio, à tem-
peratura de 15°C, espera-se observar
a) a formação de uma solução não saturada constituída
pela mistura das duas substâncias.
b) a precipitação de um sólido constituído por sulfeto
de zinco.
c) a precipitação de um sólido constituído por sulfito de
zinco.
d) a precipitação de um sólido constituído por sulfato de
zinco.
e) a precipitação de um sólido constituído por sulfeto
de sódio.
Resolução
Poderá precipitar o ZnSO3 de acordo com a equação:
ZnSO4 + Na2SO3 → ZnSO3 + Na2SO4
Cálculo da quantidade de matéria logo após a mistura:
ZnSO4 : 1 L ————— 0,10 mol
x = 5 .10–3 mol50 . 10–3L —–— x
Na2SO3 : 1 L ————— 0,010 mol
y = 5 . 10–4 mol
50 . 10–3L —–— y
Concentração dos íons Zn2+ e SO2–
3
logo após a mistura:
[Zn2+] = = 5. 10–2 mol/L
[SO2–
3
] = = 5. 10–3 mol/L
Cálculo do KPS (produto de solubilidade) do
ZnSO3 . 2H2O:
MZnSO3 . 2H2O = 181g/mol
Na solução saturada, temos:
nZnSO4 . 2H2O = = 8,8 . 10–4 mol/L
ZnSO4 . 2H2O(s) →← Zn2+(aq) + SO2–
3
(aq)
8,8 .10–4 mol –––––– 8,8 .10–4mol ––––– 8,8 .10–4mol
[SO2–
3
] = [Zn2+] = = 8,8 . 10–3 mol/L
KPS = [Zn2+] . [SO2–
3
]
8,8 . 10–4 mol
–––––––––––––
0,100L
0,16g
–––––––––
181g/mol
5 . 10–4 mol
–––––––––––––
0,100L
5 . 10–3 mol
–––––––––––––
0,100L
Solubilidade
(g soluto / 100g H2O)
0,00069
96
0,16
46
44
32
Substância
ZnS
ZnSO4 . 7H2O
ZnSO3 . 2H2O
Na2S . 9H2O
Na2SO4 . 7H2O
Na2SO3 . 2H2O
3](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-99-320.jpg)
![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
KPS = 8,8 . 10–3 x 8,8 . 10–3 =
Produto das concentrações dos íons misturados:
Q = [Zn2+] . [SO2–
3
] = 5 . 10–2 x 5 . 10–3 =
Temos, portanto:
Q > KPS
Haverá precipitação de ZnSO3.
e
Utilizando os dados fornecidos na tabela da questão 3,
é CORRETO afirmar que o produto de solubilidade do
sulfito de sódio em água, a 15°C, é igual a
a) 8 x 10–3. b) 1,6 x 10–2. c) 3,2 x 10–2.
d) 8. e) 32.
Resolução
Cálculo da solubilidade do Na2SO3 em quantidade de
matéria:
Na2SO3 . 2H2O ––––––––– Na2SO3
162g ––––––––– 1 mol
32g ––––––––– x
x = 0,2 mol
Cálculo da concentração em mol/L:
Considerando-se a densidade da solução igual a 1g/mL,
temos:
100mL –––––––– 0,2 mol
1000mL ––––––– x
x = 2 mol ∴ 2 mol/L
Cálculo do produto de solubilidade do sulfito de sódio:
Na2SO3(s) →← 2Na+(aq) + SO3
2–
(aq)
2 mol 4 mol/L 2 mol/L
PS = [Na+]2 [SO3
2–
]
PS = [4]2 . 2
PS = 32
4
2,5 . 10–4
7,7 . 10–5](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-100-320.jpg)





![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
c
Qual das opções a seguir apresenta a seqüência COR-
RETA de comparação do pH de soluções aquosas dos
sais FeCl2, FeCl3, MgCl2, KClO2, todas com mesma
concentração e sob mesma temperatura e pressão?
a) FeCl2 > FeCl3 > MgCl2 > KClO2
b) MgCl2 > KClO2 > FeCl3 > FeCl2
c) KClO2 > MgCl2 > FeCl2 > FeCl3
d) MgCl2 > FeCl2 > FeCl3 > KClO2
e) FeCl3 > MgCl2 > KClO2> FeCl2
Resolução
O ácido clorídrico (HCl) é mais forte que o ácido cloro-
so (HClO2).
O sal KClO2, por ser derivado de um ácido fraco e base
forte, sofre hidrólise alcalina.
ClO–
2 + H2O →
← HClO + OH–
Sua solução será alcalina com pH > 7 (25°C).
O sal MgCl2, por ser derivado de um ácido forte e base
forte, praticamente não se hidrolisa, e, portanto, sua
solução aquosa será neutra com pH ≅ 7 (25°C).
Nos sais FeCl2 e FeCl3, os cátions Fe2+ e Fe3+ hi-
dratados sofrem hidrólise ácida, produzindo soluções
com pH < 7 (25°C).
Devido à maior carga iônica, o íon [Fe(H2O)x]3+ é ácido
mais forte que o íon [Fe(H2O)y] 2+.
3+
1) Fe(H2O)x
→
← [Fe(H2O)x–1
OH]2+ + H+ K1
2+
2) Fe(H2O)y
→
← [Fe(H2O)y–1
OH]1+ + H+ K2 < K1
Como [H+]1 > [H+]2, podemos concluir que
pHFeCl2
> pHFeCl3
.
Ordem decrescente de pH:
KClO2 > MgCl2 > FeCl2 > FeCl3
10](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-107-320.jpg)







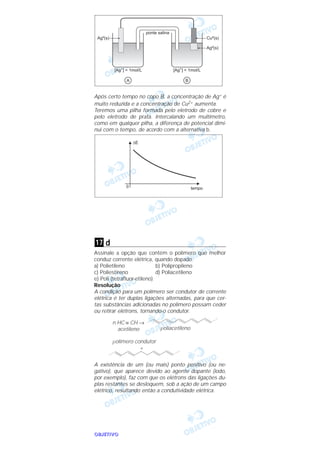
![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
a
Considere as seguintes equações que representam
reações químicas genéricas e suas respectivas equa-
ções de velocidade:
I. A → produtos; vI = kI [A]
II. 2B → produtos; vII = kII [B]2
Considerando que, nos gráficos, [X] representa a con-
centração de A e de B para as reações I e II, respectiva-
mente, assinale a opção que contém o gráfico que me-
lhor representa a lei de velocidade das reações I e II.
Resolução
Como [X] representa as concentrações dos reagentes A
e B, o seu valor diminui com o passar do tempo e a rela-
ção aumenta. Isto é observado apenas no
gráfico da alternativa a.
Para a equação I, como é de primeira ordem, teremos
curva ascendente no gráfico versus t.
Para a equação II, como é de segunda ordem, teremos
uma reta ascendente no gráfico versus t.
A tabela a seguir mostra as propriedades características
das reações do tipo R → produtos
Gráfico retilíneo
em [A] versus t
1
–––– versus t
[B]
Equação da velocidade
v = k [A]1
v = k [B]2
Ordem
1
2
1
––––
[X]
1
––––
[X]
1
––––
[X]
18](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-116-320.jpg)
![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
d
A 25°C, borbulha-se H2S(g) em uma solução aquosa
0,020 moI L–1 em MnCl2, contida em um erlenmeyer,
até que seja observado o início de precipitação de
MnS(s). Neste momento, a concentração de H+ na
solução é igual a 2,5 x 10–7 moI L–1.
Dados eventualmente necessários, referentes à tem-
peratura de 25°C:
I. MnS(s) + H2O( l) →← Mn2+(aq) + HS– (aq) + OH– (aq);
KI = 3 x 10–11
II. H2S(aq) →← HS–(aq) + H+ (aq); KII = 9,5 x 10–8
III. H2O( l) →← OH–(aq) + H+ (aq) ; KIII = 1,0 x 10–14
Assinale a opção que contém o valor da concentração,
em moI L–1, de H2S na solução no instante em que é
observada a formação de sólido.
a) 1,0 x 10–10 b) 7 x 10–7 c) 4 x 10–2
d) 1,0 x 10–1 e)1,5 x 104
Resolução
Reação entre H2S(g) e MnCl2 até precipitação de
MnS(s):
H2S(g) + Mn2+(aq) → MnS(s) + 2H+(aq)
K =
MnS(s) + H2O(l) →← Mn2+(aq) + HS–(aq) + OH–(aq)
KI = [Mn2+] . [HS–] . [OH–] = 3 . 10–11
H2S(aq) →← HS–(aq) + H+(aq)
KII = = 9,5 . 10–8
H2O(l) →← OH–(aq) + H+(aq)
KIII = [OH–] . [H+] = 1,0 . 10–14
K =
K = =
= 3,17 . 10–11 → = 3,17 . 10–11
[H+] = 2,5 . 10–7 mol/L
[Mn2+] = 0,020 mol/L
[H+]2
––––––––––––––
[H2S] . [Mn2+]
[H+]2
––––––––––––––
[H2S] . [Mn2+]
[HS–] . [H+]
[OH–] . [H+] . –––––––––––
[H2S]
––––––––––––––––––––––––––
[Mn2+] . [HS–] . [OH–]
KIII . KII
––––––––
KI
[HS–] . [H+]
–––––––––––
[H2S]
[H+]2
––––––––––––––
[H2S] . [Mn2+]
19](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-117-320.jpg)
![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
3,17 . 10–11 =
[H2S] =
[H2S] = 9,87 . 10–2 mol/L
[H2S] ≅ 1,0 . 10–1 mol/L
(2,5 . 10–7)2
––––––––––––––––––
3,17 . 10–11 . 0,020
(2,5 . 10–7)2
–––––––––––––
0,020 . [H2S]](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-118-320.jpg)


![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
Considere o elemento galvânico representado por:
Hg(l) I eletrólito || Cl– (solução aquosa saturada em
KCl) I Hg2Cl2 (s) I Hg(l)
a) Preveja se o potencial do eletrodo representado no
lado direito do elemento galvânico será maior, me-
nor ou igual ao potencial desse mesmo eletrodo
nas condições-padrão. Justifique sua resposta.
b) Se o eletrólito no eletrodo à esquerda do elemento
galvânico for uma solução 0,002 moI L–1 em Hg2+ (aq),
preveja se o potencial desse eletrodo será maior,
menor ou igual ao potencial desse mesmo eletrodo
nas condições-padrão. Justifique sua resposta.
c) Faça um esboço gráfico da forma como a força ele-
tromotriz do elemento galvânico (ordenada) deve
variar com a temperatura (abscissa), no caso em
que o eletrodo do lado esquerdo do elemento gal-
vânico seja igual ao eletrodo do lado direito nas con-
dições-padrão.
Resolução
a) O potencial do eletrodo de calomelano saturado
(lado direito) será menor que o potencial desse
mesmo eletrodo nas condições padrão. A solução
saturada apresenta maior concentração em íons
Cl–, logo, o potencial de redução será menor.
1/2Hg2Cl2(s) + e– → Hg(l) + Cl–(aq)
De acordo com a equação de Nernst, temos:
E = E0– . log [Cl–]
0,0592
–––––––
1
22](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-121-320.jpg)
![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
b) O potencial do eletrodo (lado esquerdo) será menor
que o potencial do eletrodo nas condições padrão.
De acordo com a equação
Hg2+ + 2e– → Hg(l), temos:
E = E0– . log
Quanto menor [Hg2+], menor potencial de redução.
c) Temos:
Hg2Cl2(s) ͉ Hg(l) ͉ Cl–
(solução 1 mol/L em KCl) ͉͉ Cl–
solução saturada em KCl) ͉ Hg(l) ͉ Hg2Cl2(s)
Eesquerda > Edireita
Portanto, na meia célula da esquerda irá ocorrer
redução
1/2Hg2Cl2(s) + e–
(CM)
→← Hg(l) + Cl–
(aq)
Nas condições padrão: ∆E0 = 0
De acordo com a equação de Nernst vem:
∆E = ∆E0 – . ln Q = – . ln .
Como [Cl–
]esquerda < [Cl–
]direita , ln Q < 0
∆E = . ln Q
Logo, ∆E cresce com o aumento da temperatura.
RT
––––
nF
[Cl–
]esquerda
–––––––––––
[Cl–
]direita
RT
–––
nF
RT
–––
nF
1
––––––
[Hg2+]
0,0592
–––––––
2](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-122-320.jpg)





![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
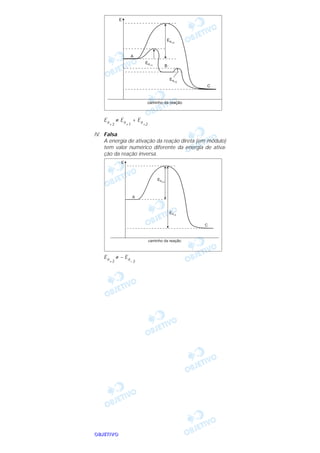
b) A energia de ativação pode ser calculada a partir
dos valores experimentais de k a várias temperatu-
ras.
No gráfico de ln k em função de 1/T, a energia de
ativação é então estimada por:
coeficiente angular = – = – tg α
c) Para determinar a ordem de uma reação, os quími-
cos plotam, de diferentes maneiras, os dados expe-
rimentais de concentração contra o tempo, até con-
seguir um gráfico retílineo.
Gráfico retilíneo
[R] versus t
ln [R] versus t
1
––– versus t
[R]
Ordem
0
1
2
Ea
–––
R
UUUUNNNNEEEESSSSPPPP ---- ((((PPPPrrrroooovvvvaaaa ddddeeee LLLLíííínnnngggguuuuaaaa PPPPoooorrrrttttuuuugggguuuueeeessssaaaa)))) DDDDeeeezzzzeeeemmmmbbbbrrrroooo////2222000000004444](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-129-320.jpg)
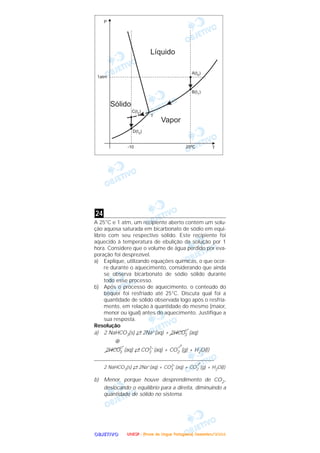
![OOOOBBBBJJJJEEEETTTTIIIIVVVVOOOO
Considere a curva de titulação abaixo, de um ácido fra-
co com uma base forte.
a) Qual o valor do pH no ponto de equivalência?
b) Em qual(ais) intervalo(s) de volume de base adicio-
nado o sistema se comporta como tampão?
c) Em qual valor de volume de base adicionado
pH = pKa?
Resolução
a) Observando-se o gráfico, nota-se um aumento ele-
vado de pH a partir de 50mL, e conclui-se que houve
a neutralização do ácido. O valor do pH no ponto de
equivalência é aproximadamente 8,5.
b) A equação química do processo é:
Ácido + Base → Sal + Água
fraco forte (caráter básico)
Antes do ponto de equivalência temos uma mistura do
ácido fraco não neutralizado e o sal formado constituin-
do uma solução tampão. Esta é observada no gráfico no
intervalo em que temos pequenas variações de pH,
aproximadamente de 10mL a 45mL.
c) Em qualquer ponto de titulação (antes do ponto de
equivalência), a concentração de íon H+ se calcula
por
HA →← H+ + A–
ácido
fraco
Ka =
[H+] = . Ka
No ponto meio de qualquer titulação de ácido fraco por
base forte, a metade do ácido foi convertida na sua
base conjugada, isto é, [HA] = [A–], portanto,
[H+] = Ka
Logo, pH = pKa
Isto ocorre com volume de base adicionado igual a
25mL.
[HA]
––––––
[A–]
[H+] [A–]
–––––––––
[HA]
29
UUUUNNNNEEEESSSSPPPP ---- ((((PPPPrrrroooovvvvaaaa ddddeeee LLLLíííínnnngggguuuuaaaa PPPPoooorrrrttttuuuugggguuuueeeessssaaaa)))) DDDDeeeezzzzeeeemmmmbbbbrrrroooo////2222000000004444](https://image.slidesharecdn.com/ita2005-130423201047-phpapp01/85/Ita2005-130-320.jpg)
