Este documento apresenta uma série de exercícios sobre relações e funções matemáticas. Os exercícios abordam tópicos como: explícitação de conjuntos e relações; domínio, contradomínio e imagem de relações; propriedades de relações como reflexividade, simetria e transitividade; definição e características de funções; composição e inversa de funções; e zeros de funções.

1. Alegri Financeir Fundamenta Médi Geometri Trigonometri Superio
Cálculos
a a l o a a r
Ensino Médio: Relações e Funções: Exercícios
Explicitando conjuntos
1. Dados os conjuntos A={a,b,c} e B={1,2,3,4}, podemos construir
a relação R em A×B que está apresentada no gráfico.
Qual resposta mostra a relação R de forma explicita?
a. R={(a,1),(b,3),(c,4),(a,3)}
b. R={(1,a),(4,a),(3,b),(c,2)}
c. R={(a,1),(b,3),(c,2)}
d. R={(a,1),(a,4),(b,3),(c,2)}
2. Com a mesma relação R do exercício anterior, qual das
alternativas é a relação inversa R-1?
a. R-1={(a,1),(a,4),(b,3),(c,2)}
b. R-1={(1,a),(4,a),(3,b),(2,c)}
c. R-1={(4,a),(2,c),(3,b)}
d. R-1={(1,a),(2,c)}
3. Sejam os conjuntos A={a,b,c,d,e} e B={2,4,6,8,10} e a relação R,
mostrada no gráfico.

2. Quais são as formas explícitas da relação R e da relação
inversa R-1?
4. Sejam os conjuntos A={1,2,3} e B={1,3,4,5} de números reais e
a relação definida por R={(x,y) A×B: y=2x-1}. Qual dos gráficos
cartesianos abaixo, representa a relação R?
5. Sejam os conjuntos A={1,3,4,5} e B={0,6,12,20} e a relação
R={(x,y) em A×B: y=x(x-1)} definida sobre A×B. Escrever R de
uma forma explicita e construir o gráfico cartesiano desta
relação.
6. Seja A={1,2,3,5,7}. Analisar o gráfico cartesiano da relação R
em A×A e responder às questões pertinentes a esta relação.
Qual das alternativas abaixo é verdadeira?
a. (2,3) R, (5,1) R, (7,7) R
b. (1,1) R, (3,5) R, (5,1) R
c. (1,1) R, (5,5) R, (3,5) R
d. (2,3) R, (3,5) R, (7,7) R

3. Dominio, contradominio, imagem, relações direta e inversa
7. Para a relação R={(1,1),(2,3),(3,5),(5,1),(7,7)} definida sobre o
conjunto A={1,2,3,5,7}, responda qual das alternativas abaixo
representa o contradomínio da relação R. (Dica: Ver o gráfico do
Exercício 6)
8. a. CoDom(R)={1,2,3,5,7}
9. b. CoDom(R)={1,3,5,7}
10.c. CoDom(R)=R
11.d. CoDom(R)={3,5,7}
12.Seja a relação R={(1,1),(2,3),(3,5),(5,1),(7,7)} def. sobre
A={1,2,3,5,7}. Qual alternativa representa o domínio de R. (Dica:
Ver o gráfico do Exercício 6)
13.a. Dom(R)=R
14.b. Dom(R)={2,5,7}
15.c. Dom(R)={1,2,7}
16.d. Dom(R)={1,2,3,5,7}
17.Para a relação R={(1,1),(2,3),(3,7),(5,1),(7,7)} def. sobre
A={1,2,3,5,7}, qual das alternativas representa a imagem de R.
(Dica: Ver o gráfico do Exercício 6)
18.a. Im(R)={1,2,3,5,7}
19.b. Im(R)={1,3,5,7}
20.c. Im(R)={1,3,5}
21.d. Im(R)=R
22.Sejam A={2,4,6,8}, B={1,3,5,7} e a relação R em A×B
apresentada pelo seu gráfico cartesiano.
Identifique se cada afirmação é V (verdadeira) ou F (falsa).
a. (2,1) pertence à relação R.
b. (3,2) pertence à relação R.
c. (4,3) pertence à relação R.
d. (5,6) pertence à relação R.
e. (8,7) pertence à relação R.
23. Usando as informações do exercício anterior, apresente o
contradomínio da relação R e a inversa da relação R, denotada
por R-1.

4. Neste trabalho, o conjunto dos números naturais será denotado
por N={1,2,3,4,5,6,7,...}.
24. Seja a relação R={(x,y) N×N: 2x+y=8}. Qual dos ítens
representa o domínio da relação R?
a. {8} b. N c. {1,2,3} d. {2,4,6}
25.Seja a relação R={(x,y) em N×N: 2x+y=8}. Qual das respostas
abaixo representa o contradomínio de R?
a. {1,3,5,7} b. {0,1,2,3,4,5,6,7} c. {0,2,4,6} d. N
26.Seja a relação R={(x,y) em N×N: 2x+y=8}. Qual das alternativas
abaixo representa a imagem de R?
a. {1,3,5,7} b. {2,4,6} c. Ø d. N
27. Seja a relação R={(x,y) em N×N: 2x+y=8}. A relação inversa
denotada por R-1 está indicada em qual das alternativas?
28.a. {(6,1),(4,2),(2,3)}
29.b. Ø
30.c. {(1,6),(2,4),(3,2)}
31.d. N
Relações reflexivas, simétricas, transitivas e anti-simétricas
16.Seja A={1,3,8} e as relações abaixo, definidas sobre A. Quais
das alternativas indicam a ocorrência da propriedade reflexiva?
17.a. R1={(1,1),(1,3),(3,3),(3,1),(8,1)}
18.b. R2={(1,1),(3,1),(1,8),(3,3),(8,8)}
19.c. R3={(3,1),(3,3),(5,8),(1,1),(8,8)}
20.d. R4={(8,8),(3,3),(1,8),(3,1),(1,1)}
21.e. R5={(8,8),(3,3)}
22.Dadas as relações definidas sobre C={1,3,5}, qual delas
alternativas mostra uma relação simétrica?
23.a. R1={(1,3),(5,3),(5,5),(3,5)}
24.b. R2={(1,3),(3,1),(5,5),(1,5)}
25.c. R3={(3,1),(3,3),(5,5),(5,1)}
26.d. R4={(1,1),(3,3),(5,5)}
27.A relação R={(1,3),(3,3),(2,4),(3,1),(2,3),(3,2)} def. sobre
A={1,2,3,4,5} é simétrica?
28.Sejam as relações definidas nos conjuntos indicados. Qual
delas é uma relação transitiva?
29.a. Ra={(2,6),(6,8),(8,2)},conjunto A={2,6,8}.
30.b. Rb={(1,3),(3,4),(1,2)},conjunto B={1,2,3,4}.
31.c. Rc={(1,3),(3,5),(1,5)},conjunto C={1,3,5}.
32.d. Rd={(1,2),(2,3),(3,2)},conjunto D={1,2,3}.

5. 33.Dado o conjunto A={1,3,8} e as relações sobre A listadas
abaixo, indique qual alternativa mostra uma relação anti-
simétrica. Justifique porque as outras relações não são anti-
simétricas.
34.a. R1={(1,3),(3,1),(8,1)}
35.b. R2={(1,8),(8,8),(1,3),(8,1)}
36.c. R3={(3,3),(1,8),(8,8),(8,1)}
37.d. R4={(8,8),(1,3),(8,1),(1,1)}
Definição de função
21.Quais dos diagramas abaixo se encaixa na definição de função
de A em B, onde A={a,b,c} e B={1,2,3}.
22. Quais dos diagramas abaixo não representa uma função de A
em B, onde A={a,b,c} e B={1,2,3}.
23.Dada a função real f(x)=2x+3 definida sobre o conjunto
A={1,2,3,4}, apresente o conjunto de todos os pares ordenados
pertencentes à função f.
24. Dada a função f:R R definida por:
determinar: f(0), f(-4), f(2) e f(10).
25.Qual conjunto é formado pelos valores f(0), f(-3), f(2) e f(10), se
a função de R×R está definida por f(x)=x²-4x+7?
26.a. {67,3,4,7}
27.b. {0,-3,2,10}
28.c. {7,28,3,67}

6. 29.d. {10,2,-3,0}
30.Calcular os valores: f(3), f(1), f(0) e f(-10), para a função real
f=f(x) definida por:
Zeros de funções
27.Por definição, zero de uma função é o ponto do domínio de f
onde a função se anula. Dadas as quatro funções:
f(x)=3x-8, g(x)=2x+6, h(x)=x-1 e i(x)=15x-30
qual dos conjuntos contém os zeros de todas as funções.
a. {-8,2,-1,-30}
b. {8/3,-3,1,2}
c. {-8/3,2,-1,-2}
d. {2,8/3,3,30}
28.Se uma função do primeiro grau é da forma f(x)=ax+b tal que
b=-11 e f(3)=7, obtenha o valor da constante a.
29.Usando f(x)=ax+b e sabendo-se que f(-2)=8 e f(-1)=2, obter os
valores de a e b.
30.Obter a função f(x)=ax+b tal que f(-3)=9 e f(5)=-7. Obtenha f(1) e
o zero desta função.
31. Para a função real definida por f(x)=x²+2x-3, obtenha: f-1(5),
f-1(0), f-1(-3) e f-1(x+3)
32. Para a função real f(x)=2x+4, qual é o conjunto f-1(8)?
33. Dada a função real f(x)=-x²+6x+3, determinar o conjunto f-1(8)?
34. Dada a função real f3(x)=x³, qual é o conjunto f-1(8)?
35.Uma sequência real é uma função real cujo domínio é o
conjunto dos números naturais. Seja a sequência real definida
por:

7. cujo gráfico é dado por
Obter os valores de f(2), f(3), f(5), f-1(8) e f-1(3/2)
36.Qual dos gráficos representa uma função sobrejetora?
37.Qual dos gráficos representa uma função injetora?
38.Seja a função f definida sobre o conjunto A={x,y,z} com imagem
em B={1,2,3}. Qual das alternativas contém os pares ordenados
(x,y) de elementos em A×B que representam uma função
bijetora (injetora e sobrejetora).
39.a. {(x,3),(y,1),(z,2)}
40.b. {(x,1),(y,2),(x,3),(z,1)}
41.c. {(y,2),(x,2),(z,3)}
42.d. {(x,1),(y,3),(z,2),(z,1)}
43.Ao analisar a função real f definida por f(x)=x²+4x-12, podemos
afirmar que f é injetora? Justifique a resposta.

8. 44.Quais das funções são
sobrejetoras?
45.a. f(x)=-x+3
46.b. f(x)=3
47.c. f(x)=x³-1
48.d. f(x)=-x²-1
Funções Compostas
41.Se f(x)=3x-5, g(x)=x²+2x-3
e (gof)(x)=g(f(x)), obter
(fog)(2), (gof)(-3), (gof)(x) e (fog)(x).
42.Sejam as funções reais definidas por g(x)= 3x-2 e
Obter (gof)(1), (fog)(3), (fof)(2) e (gog)(-4).
43. Dadas as funções f:A B e g:B C pelo diagrama
obter a função composta gof:A C.
44.Sobre o conjunto A={a,b,c,d}, definimos as funções
f={(a,d),(b,c),(c,b),(d,a)}
g={(a,b),(b,c),(c,d),(d,d)}
Determinar as compostas gof e fog.
45.Definidas as funções f, g e h, pelo diagrama:

9. determinar fog, goh, hof, gog nos pontos 1, 2 e 3.
46.Dadas as funções reais f(x)=3x-1 e g(x)=x(x+2), obter gof, fog,
gog e fof.
Operações com funções
47.Por definição (f+g)(x)=f(x)+g(x). Realizar a soma das funções f e
g é o mesmo que obter os valores de f+g em todos os pontos do
domínio comum a ambas as funções. Consideremos as funções
reais:
f={(1,2),(2,3),(3,4),(4,5)}
g={(1,5),(2,2),(3,3),(4,1)}
Qual alternativa mostra a função f+g?
a. {(1,7),(2,5),(6,7),(4,6)}
b. {(2,7),(4,5),(6,7),(8,6)}
c. {(1,7),(2,5),(3,7),(4,6)}
d. {(1,7),(2,5),(6,7),(8,6)}
48.Por definição (f-g)(x)=f(x)-g(x). Realizar a diferença entre as
funções f e g é o mesmo que obter os valores de f-g em todos
os pontos do domínio comum a ambas as funções. Sejam as
funções reais:
f={(1,2),(2,3),(3,4),(4,5)}
g={(1,5),(2,2),(3,3),(4,1)}
Qual alternativa representa a função f-g?
a. {(0,-3),(0,1),(0,1),(0,4)}
b. {(1,3),(2,-1),(3,-1),(4,-4)}
c. {(1,3),(2,1),(3,-1),(4,4)}
d. {(1,-3),(2,1),(3,1),(4,4)}
49.Por definição (f.g)(x)=f(x).g(x). Realizar o produto das funções f
e g é o mesmo que obter os valores de f.g em todos os pontos
do domínio comum a ambas as funções. Consideremos as
funções reais:

10. f={(1,2),(2,3),(3,4),(4,5)}
g={(1,5),(2,2),(3,3),(4,1)}
Qual alternativa representa a função f.g?
a. {(1,7),(4,6),(9,12),(16,5)}
b. {(1,10),(2,6),(3,12),(4,5)}
c. {(1,10),(4,3),(9,12),(16,5)}
d. {(1,10),(4,3),(3,12),(4,5)}
50.Por definição (f/g)(x)=f(x)/g(x). Realizar a divisão entre as
funções f e g é o mesmo que obter os valores de f/g em todos os
pontos do domínio comum a ambas as funções. Consideremos
as funções reais:
f={(1,5),(2,3),(3,9),(4,5)}
g={(1,5),(2,2),(3,3),(4,1)}
Qual alternativa representa a função f/g?
a. {(1,1),(1,3/2),(1,3),(1,5)}
b. {(1,1),(2,3/2),(3,12),(4,5)}
c. {(1,1),(4,3/2),(9,12),(16,5)}
d. {(1,1),(2,3/2),(3,3),(4,5)}
51.Determinar f+g, f-g, f.g e f/g, para as funções reais:
f={(1,4),(2,5),(3,12),(4,2)}
g={(1,4),(2,2),(3,3),(4,6)}
Gráficos de funções
52.Observe os gráficos e relacione os mesmos com as respectivas
funções:
a. f(x)=x³-4
b. g(x)=5
c. h(x)=2x+3
d. t(x)=x²-2
53.Em cada gráfico, analise o intervalo de crescimento e de
decrescimento.

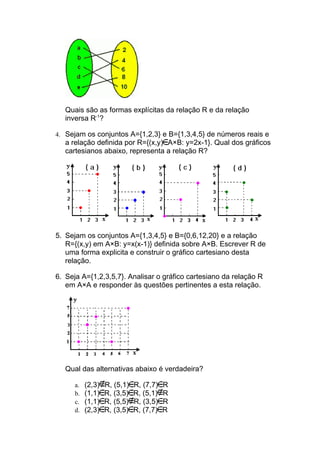
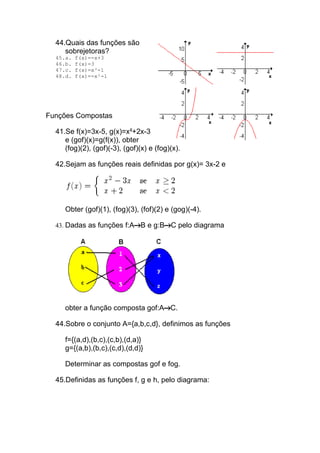
11. a) f(x)=x³ b) g(x)=x² c) h(x)=3x-15 d) f(x)=-2x
54.Em cada gráfico, analise o intervalo de crescimento e de
decrescimento.
a) f(x)=-x²+4x-4 b) g(x)=3/x c) h(x)=2
55. Analisar as funções apresentadas e identificar os seus
respectivos domínios. Aqui estamos usando R[z] para a raiz
quadrada de z>0.
a. f(x)=4/(x-5)
b. g(x)=R[x+3]
c. h(x)=14x-12
d. f(x)=3x+5x1/3-4
e. g(x)=8x-3x²-16
56.Determinar a imagem para cada função:
a) f(x)=x+1 b) g(x)=3 c) h(x)=x²+2
57.Determinar as imagens para as funções: f(x)=sen(x) e g={(-2,-2),
(-1,2),(0,4),(1,1),(2,3),(3,3)}.

12. 58.Qual é a imagem da função f(x)=(x-1)(x-5) definida sobre o
conjunto D={1,2,3,4,5} que é o domínio de f.
59.Construir um esboço gráfico para cada função:
a. f(x)=|x-2| b. f(x)=|x|+3 c. f(x)=|x+2|-2
60.Sejam as funções f(x)=2x-4 e g(x)=3x+a. Se f(1)-g(0)=6, quanto
vale f(2)+5g(7)=?
a. -8 b. 65 c. 0 d. 13
61.O vértice de uma função quadrática (do segundo grau) da forma
f(x)=ax²+bx+c pode ser obtido por:
onde =b²-4ac é o discriminante da função f. Para cada uma
das funções abaixo, obtenha o vértice da parábola.
a. f(x)=x²-10x+21
b. g(x)=x²-2x
c. h(x)=x²-1
d. m(x)=x²+14x+49
62.Os zeros de uma função quadrática f(x)=x²+bx+c são p=-7 e
q=-1. Obter o vértice da parábola que representa o gráfico desta
função.
63.Os zeros da função quadrática f(x)=ax²+bx+c, são p=2 e q=1 e
seu vértice está em (3/2,-1/4). Qual é a respectiva função?
Construída por Daiane A.Miliossi Morais, Ulysses Sodré e Sônia
F.L.Toffoli
Atualizada em 09/jul/2010.Atualizada em 24/mar/2005.